基于人工智能的建筑施工计划优化方法研究

倪秉良

规模较大、功能较复杂的建筑工程项目在施工上具有很高的复杂度。为保证项目的施工质量，避免因施工计划错误而延误工程进度，在施工前要制定合理的建筑施工计划。近年来，国内外研究人员在建筑施工计划优化方面进行了大量的研究，目前已发展至智能计算阶段。因此，应当基于人工智能算法对建筑施工计划优化做进一步探究。

1 项目概况

某高校拟新建一个研究实验基地，该项目总面积约为4500 m2，包括多个不同功能的试验区域。各个试验区域对光照、温度、湿度等要素的需求存在一定差异，因此该项目施工复杂度和难度较高，包含的工序类型和数量较为繁多，对于各个科目的要求也较多，导致整体施工流程较为繁琐，难以通过常规的方法进行施工计划优化[1]。为此，施工单位决定应用人工智能算法，优化该项目的建筑施工计划，以提升建筑施工的效率、质量和安全性等多方面的指标。

2 项目施工计划优化流程要点

2.1 施工计划编制

为保证施工计划中各个步骤均能够合理的进行，施工单位决定采用网络计划图工具编制施工计划。本次使用双代号网络图初步描述该项目的施工安排[2]。通过分析以往类似项目的施工经验以及相关文献资料，明确本项目施工中有关工序的优先级排布，编制施工作业的初步网络计划。

在得到初步网络计划后，进一步调整时间参数。每个节点均表示其对应工序的“开始事件”或“结束事件”，每类事件均具有一个最早发生时间（Earliest Time，ET）和最晚发生时间（Lastest Time，LT）。研究人员基于以往经验、专家知识和类似项目的历史数据，导入项目管理软件进行初步计算，最终确定该项目工期理论上的最小完成时间为158 d[3]。甲方要求该项目在200 d 内完工，因此计划工期可在158 ～200 d 内进行合理调整。

2.2 资源约束分析

此次建筑施工项目因其自身特性需兼顾的要求较多，不仅需要在甲方要求的时间内完成，而且需要将消耗的材料和资金成本控制在相对较低的水平，属于典型的多目标规划问题，常规的多项式算法难以取得最优解[4]。

根据本项目特点，研究人员确定用粒子群优化算法（Particle Swarm Optimization，PSO）进行求解，主要优化目标是工期最小、费用最低和资源均衡。首先，研究人员结合实际情况分析本次项目施工中的资源约束。参考图1 中的双代号工程网络，将其命名为G= （V，E）。其次，集合V中的所有元素均为时间节点，用以标记每个工序启动和完成所对应的时刻；E则用于描述边集合，表示需要消耗一定施工时间的某个工序环节。由此应用式（1）～式（6）建立数学模型。

图1 粒子编码结果（来源：作者自绘）

式中：Tp为项目施工计划消耗时间，即优化目标1；Si为事件Vi的发生时刻，i∈N*，N*为正整数集合；N为施工环节开始、结束时刻的节点总数[5]。

式中：Sj为事件j的发生时刻；Di-j为工序i→j的估算施工时间。

式中：Tr为项目施工允许的最长时间，本次为200 d。

式中，Rt k为第k类资源在工期第t天可提供的总量，k∈N*；K为项目施工使用的材料和设备种类数。

式（1）～式（3）均为优化目标表达式，分别表示工期最小化后的消耗时间、最小化的项目费用以及最小化的资源使用方差。

式（4）～式（6）作为约束条件，主要进行3 个方面的约束：

1）确保各个环节按照优先级从高到低的顺序进行，避免混乱；

2）确保了项目施工时间不超过200 d；

3）资源方面的约束[6]。模型中涉及的具体相关变量数据，通过专家经验法分析历史数据获得。

2.3 粒子群算法设计

根据上文所描述的多目标施工计划优化问题，应当采用人工智能算法进行有效解决[7]。为此，研究人员应用粒子群优化PSO 算法进行求解，主要可通过如下步骤实现：

1）在PSO 算法中对粒子进行编码。结合本次研究的施工计划优化问题，采用矩阵编码形式作为编码方案。其中，矩阵的行数为本工程项目中的工序数量，列数与项目的要求工期天数相同。在该矩阵下元素仅有两类，以“1”表示存在施工行为，“0”表示不存在施工行为。本次施工的粒子编码结果如图1 所示。

2）基于粒子编码结果，研究人员进一步对运算符进行重载，以实现粒子位置的更新要求。重载环节主要分为3 个步骤：第1，减法运算。随机选取粒子的某两个位置的编码，定义二者之差仍然为矩阵，找出被减数与减数之间的“差别”，确保粒子在后续的迭代计算中调整自身运行方向。第2，乘法运算。当随机变量减法运算完成后，应用乘法运算对运算结果重新进行定位（该定位结果属于随机变量），以避免粒子后续运行方向出现错误[8]。第3，加法运算。作用于速度和乘法运算之积与原始位置与更新后的速度之间，主要作用是加速粒子的后续迭代进程，同时避免粒子因落入局部最优解而无法继续运算。针对本次施工的实际需要，将施工消耗时间、施工成本和资源均衡分配所需要的算法粒子比例分配为4 : 3 : 3。

2.4 算法的其他参数设计

在粒子位置、速度编码和相应操作方法均已明确后，为进一步提升粒子群算法的效率和准确度，研究人员从以下4 个方面对算法的其他相关参数进行设计：

1）针对PSO 算法中的种群大小即“粒子数量”，综合考虑算法的搜索范围和搜索能力两方面的要求，设定该算法中的种群大小为30。

2）选取权重系数、学习因子两方面参数。前者决定当前一代的算法迭代更新速度，后者则作为影响下一代迭代速度的判断依据[9]。结合建筑项目施工管理的一般经验，将以上两方面参数均设置为1，这表示权重系数和学习因子对下一代速度的影响是等效的，不存在差异。

3）确定算法的停止准则条件。在综合考虑算法运行效率和准确性的基础上，确定本次PSO 算法在进行500次迭代计算后停止，此时算法输出当前已获取的全部帕累托最优解。

4）对各个目标进行粒子分配。

2.5 PSO算法的主要流程设计

结合本次项目施工的实际需要，参考施工计划优化相关文献后，确定本次PSO算法主要分为以下几个步骤。首先，确定输入量与输出量。其中，输入量为描述项目的双代号网络计划图G=（V，E），输出量则为遍历过程中找到的全部帕累托最优解。其次，由PSO 算法自动生成30 个粒子，并对各个粒子进行随机编码和随机初始化[10]。再次，设置迭代轮次序数t的数值为1，并按照2.3 章节中描述的运算符重载规则进行迭代更新，每进行一次迭代更新，t值增加1。最后，当t值到达设定的迭代次数上限500 次后停止运行，输出遍历过程中找到的全部的帕累托最优解。具体流程图如图2 所示。为实现上述算法流程，本次以C++语言按照流程编写对应代码，将其安装于计算机设备，实现PSO 算法的有效运行。

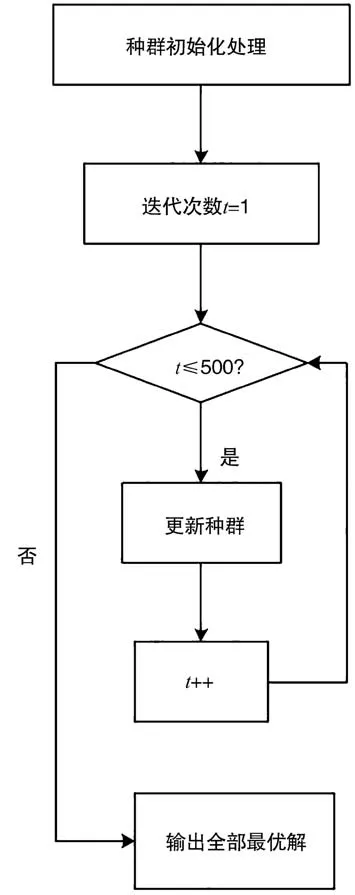
图2 本次PSO 算法的主要运行流程（来源：作者自绘）

3 优化结果与方案筛选

在上述PSO 算法全部设计完成后，研究人员在计算机上运行PSO 算法，系统自动得到备选的11 个优化方案，具体可从表1 中的数据变化趋势来看，工期和项目费用之间存在较为突出的负相关性，缩短工期对成本的增加有较为显著的影响。同时，资源均衡度指标与项目工期之间也存在较为明显的负相关，表明追求工期比较容易造成资源使用不均衡的问题[11]。

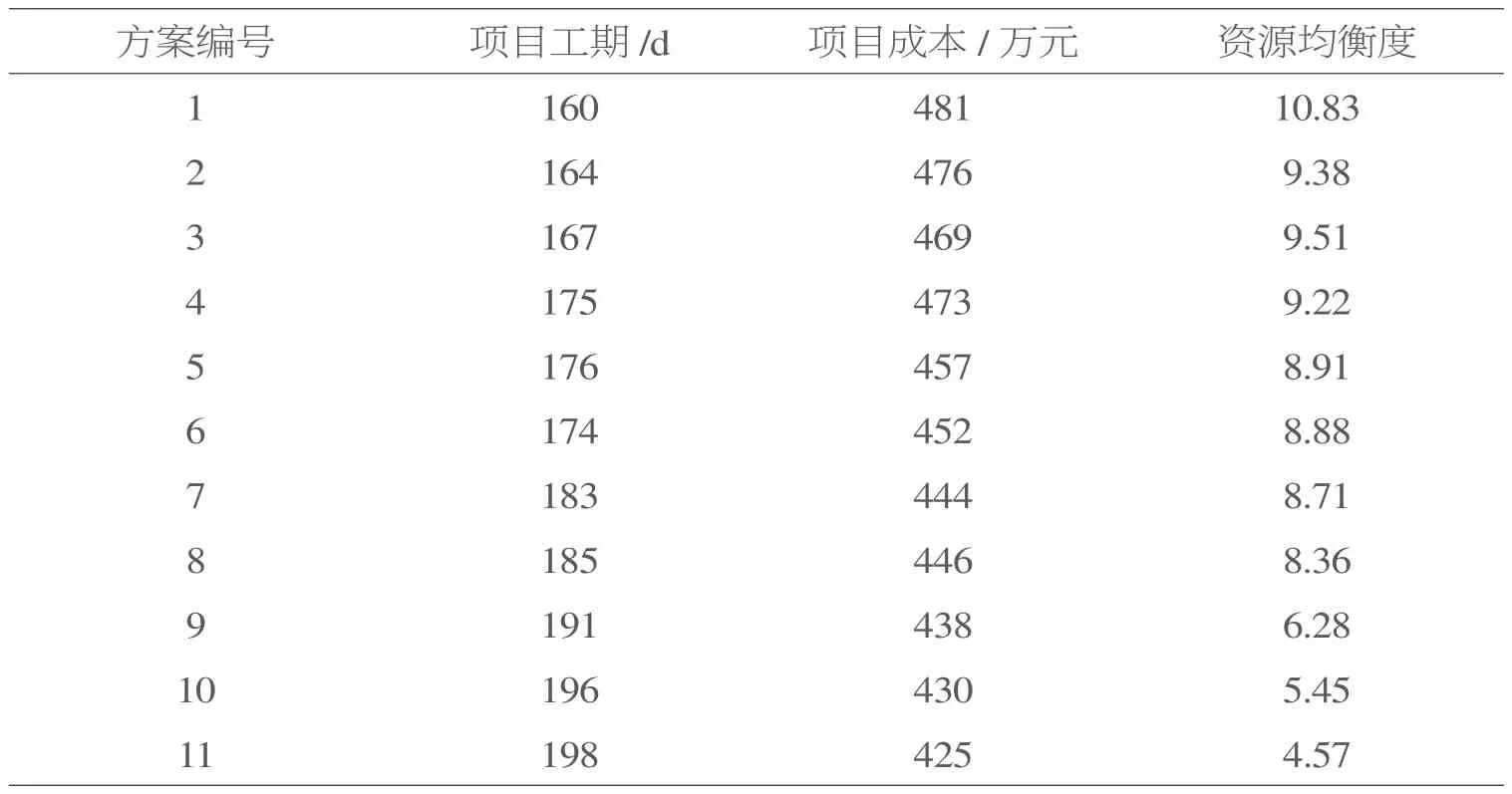
表1 基于PSO 算法求得的施工计划优选方案

针对上述特点，结合项目甲方和施工方的实际需求做进一步分析，兼顾甲方对项目施工时间和乙方对项目成本方面的要求，最终筛选出“工期平均―费用平均”的施工方案。

根据优化后的施工计划，施工单位有序进行各环节施工作业。在保证施工质量符合预期的前提下，整个项目在174.5 d 内完成，消耗成本为452.082 万元，兼顾了施工工期与施工成本开支两方面的目标。同时，施工消耗时间与成本两项指标也与PSO 算法运行得到的理论预测值较为接近，进一步证明了本次人工智能算法在施工计划优化方面的有效性。

4 结语

整体来看，本次研究以人工智能算法中的粒子群优化算法为主要工具，针对某试验基地建设项目施工计划优化方法展开研究，通过该算法的流程得出优化后的可行施工方案，实践也证明了该次基于人工智能算法优化建筑工程项目施工计划的有效性和准确性。本次研究难免存在不足之处，在今后的研究中，仍需在已有粒子群算法的基础上进一步寻求改进方法，以消除可能存在的问题，如计算空间浪费、陷入“局部最优”等，有效提高研究工作的效率和精准度。