基于多指标决策的复杂网络节点识别

王力梅

(天水师范学院 数学与统计学院,甘肃 天水 741001)

近年来,利用复杂网络的多项指标进行多属性决策成为了识别关键节点的热点.韩忠明教授团队提出了面向结构洞用复杂网络的7种指标识别关键节点的方法[1].文献[2]将结构洞融入多个指标来研究军事指挥控制网络.之后,学者将结构洞指标用于生物网络领域的蛋白质识别.虽然很多学者提出了不同的基于结构洞的多属性节点识别方法,但是大多数方法主要在理论研究方面,没有应用到实际网络.基于此,本文针对2020年的新冠疫情形势下抗疫和防疫两个阶段,借助科研网络数据,提取关键词构建复杂网络.利用复杂网络的中心性、核数和结构洞等9种指标对关键词网络进行分析,运用模糊综合方法得到节点重要性排序,从而得到此阶段新冠疫情的研究热点,同时引入战略坐标方法分析聚类主题的演变.

1 网络特征与指标

以“COVID-19 和新冠肺炎”为检索词,共得到3 448篇相关文献,具体检索结果如表1所列.提取其中的关键词构建网络.本文将数据分为两个阶段,2020年1月至5月,在此时期全国中小学未全面复学,视为抗疫阶段,搜索得到的数据有1 716篇文章.2020年6月至10月底(数据搜索截至时间),在此时期全国学校已经基本复学,各个行业也已经复工复产,本阶段的关键在于预防,将其视为防疫阶段,搜索得到的数据有1 732篇文章.

1.1 网络结构

基于网络模型G={V,E},其中V表示网络节点集,E表示网络的边集,构建邻接矩阵D.抗疫阶段和防疫阶段的网络拓扑结构如图1和图2所示,两阶段网络特征数据如表2所列.

图1 抗疫阶段节点网络拓扑结构

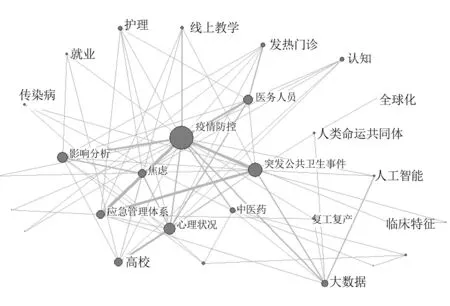
图2 防疫阶段节点网络拓扑结构

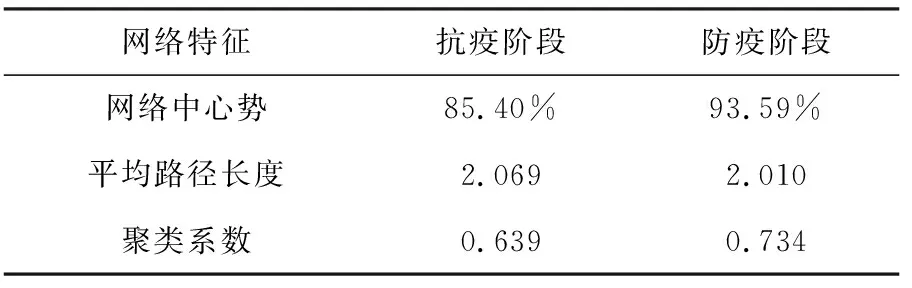
表2 两阶段网络特征对比

由表2可见,防疫阶段的网络平均路径较小,平均聚类系数较大,网络中心势较大,由此可知防疫阶段的小世界网络特征较抗疫阶段更加明显.防疫阶段网络更为集中,联系紧密,从而可知关于新冠肺炎的科研热点研究也更为聚集.

1.2 度分布

复杂网络描绘关键词之间的连接关系(本文网络为无向网络),用关键词出现的频次来表示该节点在网络中的度值.网络中节点分布如果满足幂律分布y=tx-r,其中t为常数,r为指数变量,则认为该网络为无标度网络.抗疫阶段和防疫阶段的度分布结果如图3和图4所示.

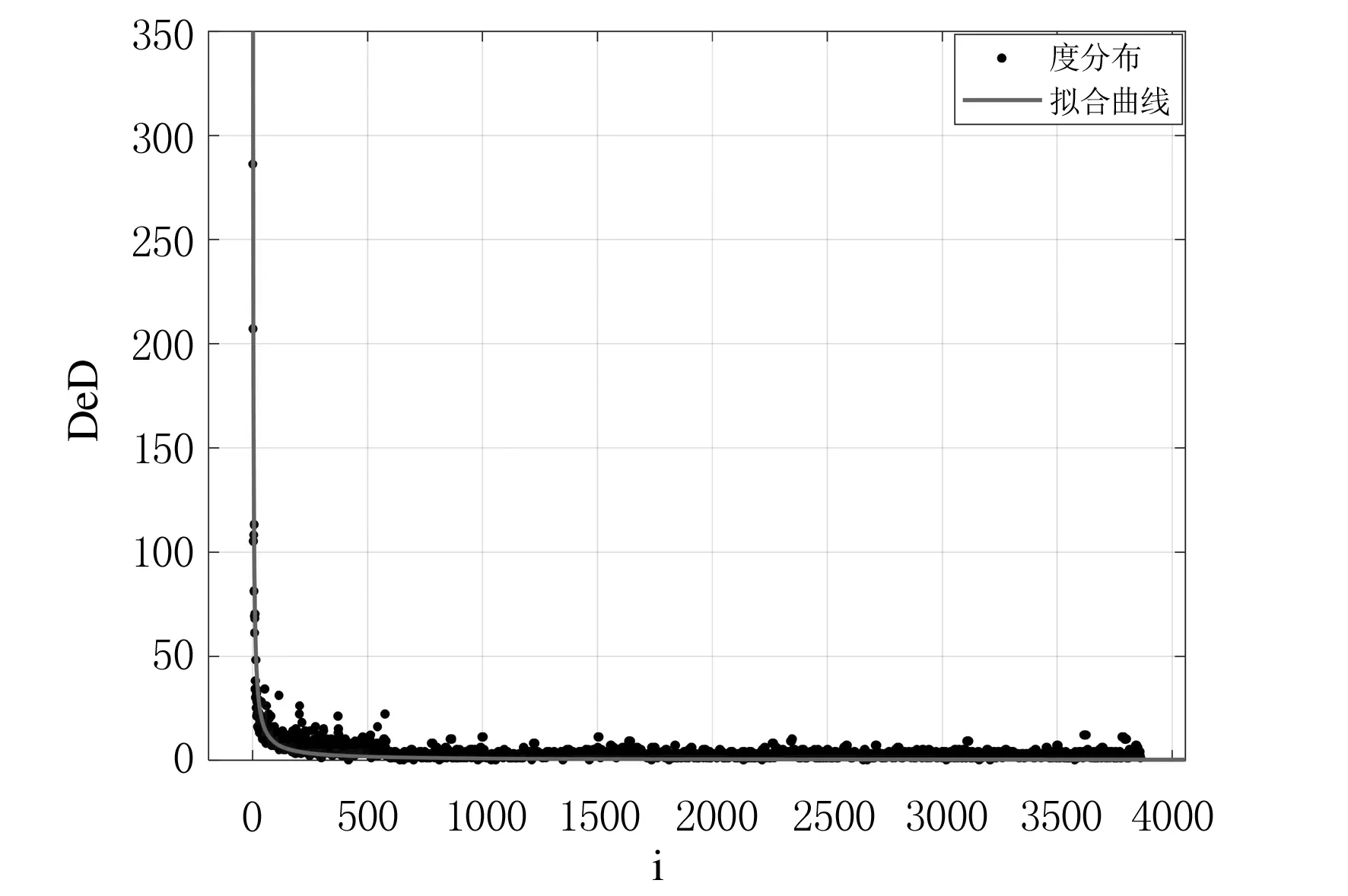
图4 防疫阶段度分布

如图3节点度的幂率拟合曲线所示,可以看出网络的节点度分布基本上符合幂率分布,且可决系数R2(即幂函数拟合度)为0.8031,计算公式为:

(1)

从图4可以看出,防疫阶段的节点度分布满足幂率分布且拟合度较高(R2为0.7443),明显呈现无标度网络的特征,适用于复杂网络的各种测度.

1.3 节点识别指标

本文中节点的网络中心性反映的是此关键词在研究中的相对重要性.中心性分为两大类,一类是基于网络整体的表征,如接近度中心性和中介中心性;另一类是基于邻节点的表征,如度中心性和特征向量中心性.

度中心性是基于邻节点个数的一种排序,表达式为:

(2)

介数中心性是基于网络的整体,计算网络中所有的节点对之间的最短路径数目,表达式为:

(3)

接近度中心性体现了本文中关键词在整个网络中居于中心的程度,表达式为:

(4)

特征向量中心性是比较网络中节点连接到影响力节点概率的一种测度,表达式为:

Ax=λx,

(5)

其中,A为节点的邻接矩阵,各个特征向量将对应各自不同的特征值λ.

结构洞表征的是处于网络中“洞”,即网络中连接那些没有关联节点的桥梁节点,连接越多的节点(即洞)在网络中所能获得的信息越多,影响力越大.本文采用Burt方法,该方法中结构洞节点受到自身4个因素作用,主要包括有效规模、效率、限制度以及等级度,其中有效规模计算公式为:

(6)

其中,j表示与i相连的节点,q表示除了i,j的所有点.效率表征的是有效规模与实际规模的比值.

限制度表征的是节点运用网络中结构洞的能力,表达式为:

(7)

其中,piq表示节点i的所有连接关系中与q相关的比例.

等级度表征的是节点对网络的控制力,控制力越大,则该关键词在研究中越处于核心位置,计算公式为:

(8)

其中,C/N表示节点限制度的均值.

核数表征的是节点在网络中的位置,核数小的节点位于网络边缘,反之则处于核心位置.

计算上述各项指标,部分抗疫阶段测试结果如表3所列.

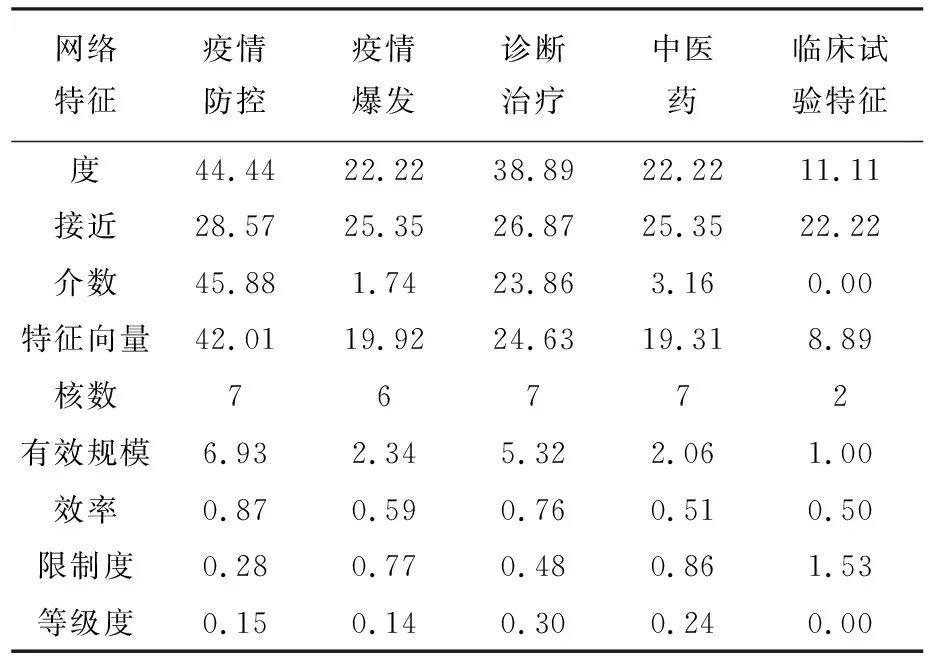
表3 抗疫阶段网络基本特征

2 多属性决策的节点识别

(1)指标精简

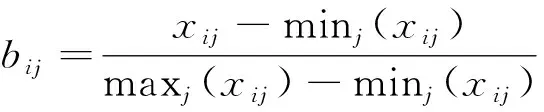
(9)

(2)组合赋权

对剩余指标归一化处理后利用熵权法和CRITIC法对各指标进行组合赋权.两种方法都是基于客观数据,但是侧重点不同,组合赋权更有利于提高合理性[4].

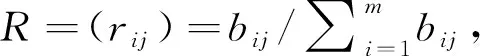
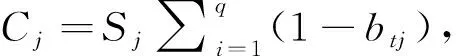
组合赋权:组合赋权采用加权平均法φj=αωj+βθj,其中α,β采用变异系数法确定.

(3)模糊综合

把指标的隶属度函数值与其相应的权重通过模糊合成算子综合计算[5].由于指标间量纲不同无法定量比较,隶属度函数可以使异质指标同质化.正指标采用半梯形偏大型隶属度函数A1(x),负指标采用半梯形偏小型隶属度函数A2(x).由此得到模糊矩阵A.具体计算公式为:

(10)

(11)

进而计算模糊集H=A⊙Φ,⊙为模糊合成算子M(;+);Φ为指标相应的权重.

计算可得指标间特征向量中心性与核数的相关系数为0.93,中介中心性与有效规模的相关系数为0.96,故去掉指标特征向量中心性和有效规模.

剩余指标由熵权法所得权重依次分别为:0.1026,0.0544,0.4388,0.1464,0.1560,0.0489,0.0529;而采用CRITIC法所得的权重依次为:0.12,0.10,0.10,0.20,0.15,0.16,0.16.综合可得Φj依次为:0.0183, 0.0482, 0.3416, 0.0590,0.3118,0.1151,-0.059.

经模糊综合后的前6排序为:疫情防控、诊断治疗、国务院、护理和人民政府及应急管理.而度中心排序的关键节点为:疫情防控、诊断治疗、失业保险金、社会保险费、社会保险补贴和人民政府.

同理可得,防疫阶段模糊综合后的关键词前6排序为:疫情防控、突发公共卫生事件、中医药、心理状况、临床特征和影响分析.

(4)验证识别关键节点

利用网络的鲁棒性验证本文方法的有效性,采取攻击特定节点来比较网络连通比例,连通比例下降越大说明失去该节点网络的性能越差,节点越为重要.采用度中心性的节点排序作为本文多属性决策方法的对比,攻击网络两种排序前2到6的节点对比情况如图5和图6所示.

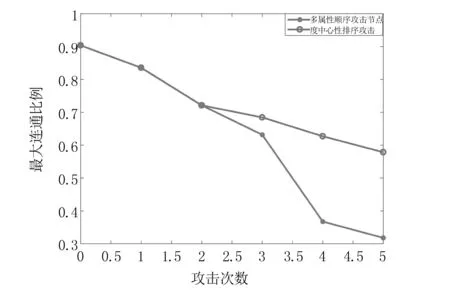
图5 抗疫阶段两种蓄意攻击对比

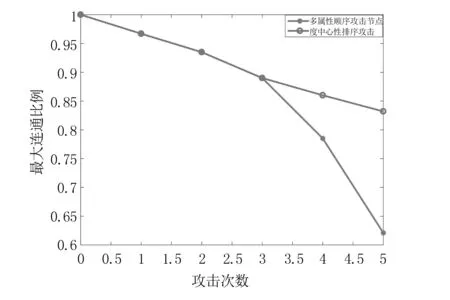
图6 防疫阶段两种蓄意攻击对比

从图5左边部分可知,本文所提方法从第3次攻击开始网络的最大连通比例开始陡降,表明多属性决策节点排序较度中心性排序更优.

从图6可以看出本文排序与度排序攻击节点相比,本文方法从第4次攻击开始显示更大破坏性,识别的节点更重要.

3 多属性聚类

将抗疫阶段的相似度矩阵导入SPSS软件中,进行系统聚类,聚类的选择标准为平方欧式距离.为了能够统一处理数据则需要进行数据标准化,标准化过程采用Z分数方法.再根据战略坐标理论计算各聚类的向心度与密度,具体聚类参数如表4所列.

表4 抗疫阶段聚类参数

研究主题聚类内部和聚类之间的联系与变化状况如图7所示[7].横坐标表示向心度,纵坐标为密度.聚类的向心度越大,表示该类团与其他聚类的联系越强,表明该聚类在新冠肺炎领域的研究中属于研究热点,处于网络的核心地位.聚类密度越大,表明该聚类内部关联更加紧密,在新冠肺炎领域的研究较为全面.

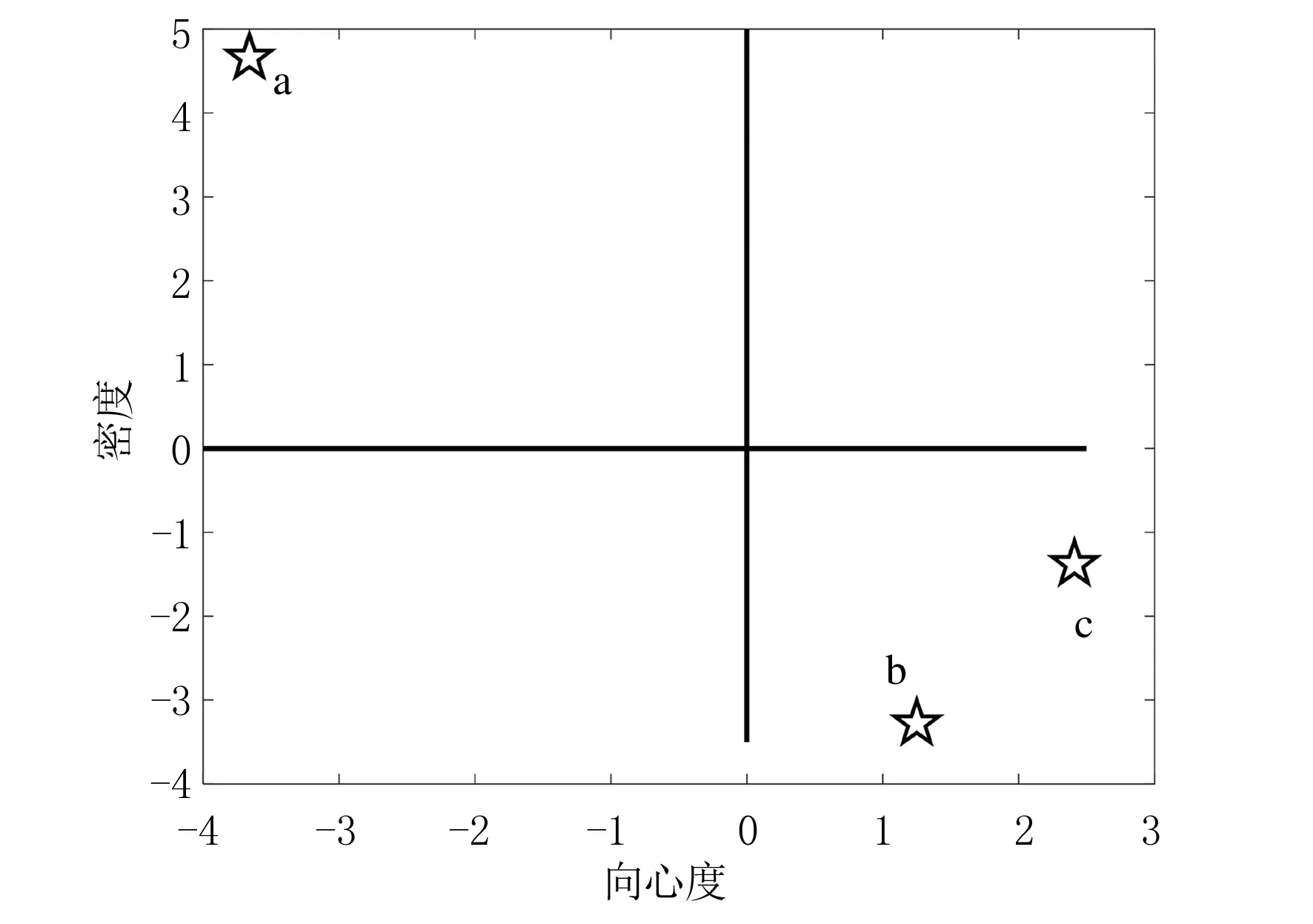
图7 抗疫阶段战略坐标

由图7可知c的向心度最大,因此中医药诊治是该时期至关重要的研究重点.a的密度最大,表明突发卫生事件及应急管理较其他聚类的内部关联最紧密,研究更为具体深入.a处于防疫时期战略坐标图的第二象限,说明在此时期突发卫生事件及应急管理已有一定发展;聚类b和c处于第四象限,说明社会保障和中医药诊治虽处于核心位置却没有得到很好的研究,应加以重视.同样的方法,得到防疫阶段的系统聚类和战略坐标,如图8所示.

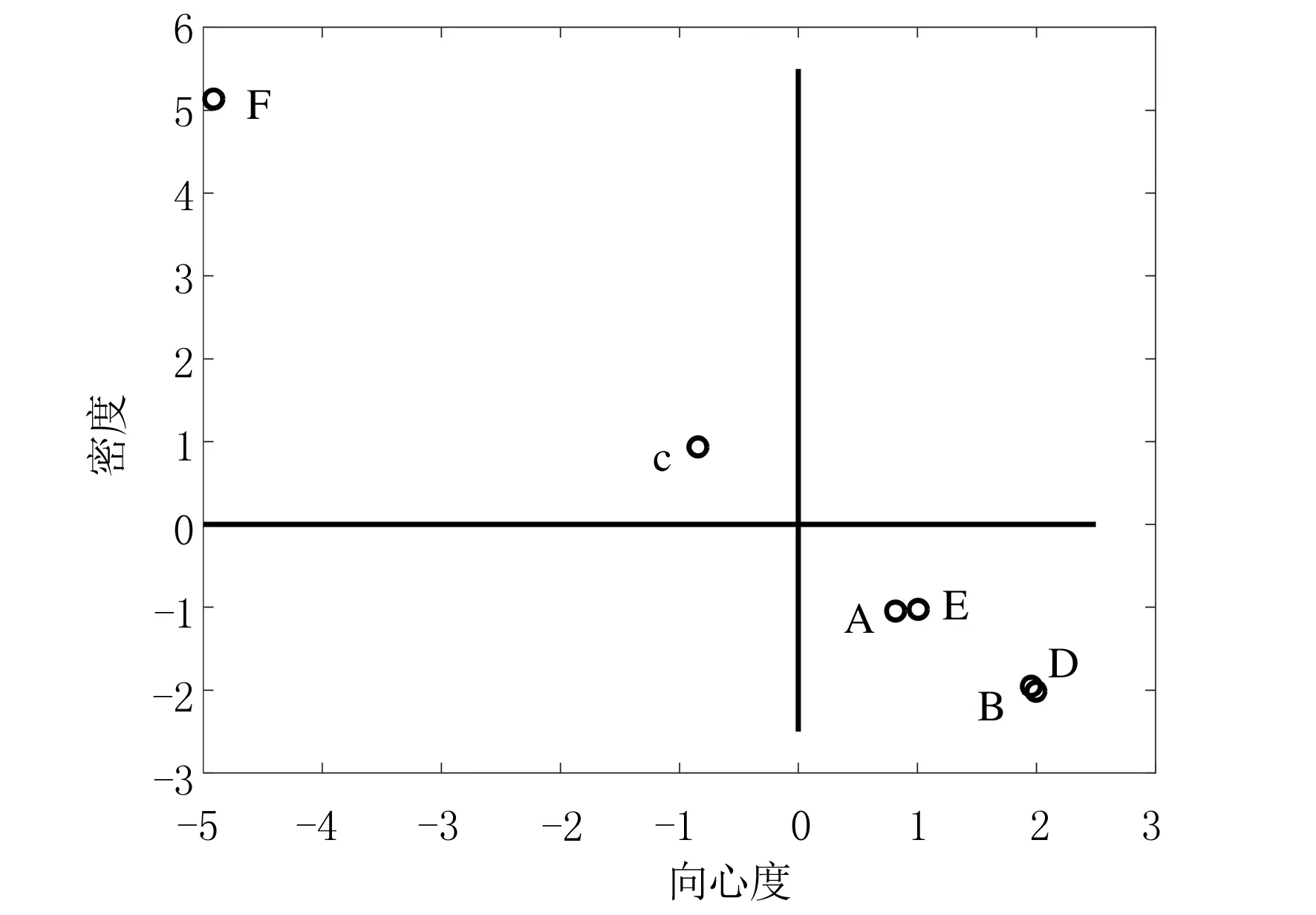
图8 防疫阶段战略坐标

由图8可知F的密度最大,表明复工复产复学及影响分析在此时期的研究较多,成熟度较高,说明该研究主题在本阶段得到较好的发展 .B和D的密度最小但向心度却最大,体现了医院防疫和科技防疫虽然是本阶段研究最为核心的部分,但是却没有得到良好的发展,是我们今后的研究重点.关于新冠肺炎的现代科技防疫如利用大数据和人工智能抑制疫情的扩散,是防疫阶段的重点.

A和E处于第四象限,向心度高但是密度低,说明突发卫生事件及应急管理与心理健康是本阶段的研究热点,但关于该主题的研究并不完善,在后续研究中要重点突破.聚类C处于第二象限,密度高但向心度低,表明中医药诊治在前面的研究中有了一定成效,不再是防疫阶段的研究核心.

a和A虽处于不同阶段但研究主题大体一致,从抗疫阶段的第一象限转为防疫阶段的第二象限,表明其在新冠肺炎研究领域的地位得到提升,成为现阶段的研究核心.c和C的研究主题为中医药诊治,从抗疫阶段的第四象限转为防疫阶段的第二象限,表明其在研究领域的地位从核心转为边缘.

4 结语

本文利用多指标识别新冠疫情形势下科研网络的关键节点,针对复杂网络的中心性、结构洞以及核数这3种属性,结合网络中心性和拓扑结构进行分析得到9个指标.进一步运用模糊综合方法建立节点识别体系,得到不同阶段的节点排序即新冠的科研重点排序.同时进行多指标决策聚类分析,得到聚类主题战略坐标图,数值结果验证了所提方法的有效性.