Commensurate and incommensurate Haldane phases for a spin-1 bilinear–biquadratic model
2023-10-11YanWeiDai代艳伟AiMinChen陈爱民XiJingLiu刘希婧andYaoHengSu苏耀恒
Yan-Wei Dai(代艳伟), Ai-Min Chen(陈爱民), Xi-Jing Liu(刘希婧), and Yao-Heng Su(苏耀恒)
1Centre for Modern Physics and Department of Physics,Chongqing University,Chongqing 400044,China
2School of Science,Xi’an Polytechnic University,Xi’an 710048,China
3The School of Materials Science and Engineering,Chongqing Jiaotong University,Chongqing 400044,China
Keywords: commensurate and incommensurate phases, symmetry-protected topological phase, transversal spin correlation
1.Introduction
Quantum phase transitions are always a hot topic of interest in condensed matter physics,which are driven by quantum fluctuations due to the uncertainty principle in quantum mechanics.One of the targets is towards completing classification of quantum states of matter.[1]In 1983,Haldane[2,3]conjectured that the half-integer spin antiferromagnetic Heisenberg chain is gapless, and the integer spin chain has an energy gap between the ground state and the first excited state.For the spin-1 Heisenberg chain, a symmetry protected topological (SPT) phase, i.e., the Haldane phase, induces a longrange string order,due to the hidden symmetry of fully brokenZ2×Z2.Interestingly,the Haldane phase in the spin-1 bilinearbiquadratic (BLBQ) model displays two parts in the structure of the Haldane phase,[4–7]i.e.,the commensurate Haldane(HaldaneC) phase and incommensurate Haldane (HaldaneIC)phases.
Let us recall the ground state phase diagram of the spin-1 BLBQ model with the Hamiltonian described as
whereSidenotes the spin-1 operator at lattice sitei,andα=tanφis the control parameter.The model has been investigated extensively using analytical and numerical methods,[8–20]exhibiting rich physics.Its ground state phase diagram has been mostly understood.Atφ=0, the model corresponds to the spin-1 Heisenberg antiferromagnet, and forφ=π/4, the model has been exactly solved by Sutherland,[21]who in turn justified the presence of the critical phase with central chargec= 2[20]forπ/4≤φ <π/2.The model exhibits SU(3)symmetry[22,23]atφ=±π/2,π/4,and-3π/4,and a gapless ferromagnetic phase with a multi-fold degenerate is detected fromφ=π/2 toφ=-3π/4.Forφ=-π/2 the model has been solved by Takhtajan and Bubujian,[24,25]which turns out to be the SU(2) WZW model at levelk=2, with the central chargec=3/2.Atφ=-π/4,Barber and Batchelor[26]solve the model in terms of the Bethe ansatz, which indicates that the dimerized phase exists nearby.Whether or not the phase transition from the gapless ferromagnetic phase to the dimerized phase is direct remains controversial.However,this controversial problem has been solved in our previous work.[16]Reference[16]showed the absence of a critical nematic phase in the vicinity of an SU(3)ferromagnetic point(φ=-3π/4)by means of tensor network algorithms.At the SU(3) ferromagnetic pointφ=-3π/4,the ground state wave function is highly degenerated, which is scaled but not conformally invariant, with the fractal dimensiondfbeing equal to 2.In addition, forφ= arctan(1/3), the model has been exactly solved by Affleck, Kennedy, Lieb, and Tasaki (AKLT),[27]with its ground state being the valence-bond-solid state.For-π/4<φ <π/4, the model is in the gapped Haldane phase with hidden topological order;[3,28]the gapped Haldane phase can divide into two subphases (HaldaneCand HaldaneIC) by the AKLT point.
The transitions between commensurate and incommensurate are important problems in quantum many-body spin systems and are induced by frustration.Physically, “incommensurate”means that the wavelength of the oscillation pattern is not an integer multiple of the lattice spacing.Normally, it is not easy to characterize the incommensurate phase.Therefore, characterization of the commensurate and incommensurate phases is an important problem in physics.Here, we focus on the gapped Haldane phase for-π/4<φ <π/4.Murashimaet al.[4]characterized the HaldaneC–HaldaneICchange by analyzing the energy gap of edge states.F´athet al.[5]proposed an effective field theory to explain these features in the HaldaneC–HaldaneICchange of the spin-1 BLBQ chain.In addition, Nomura[6]proposed a mechanism to explain the onset of the incommensurability and the shortest correlation length at AKLT point and a simple random-walk-type argument is proposed to explain the HaldaneC–HaldaneICtransition in Ref.[7].Our characterization in this study is a numerical method from the tensor network in that we use the transversal spin correlations〈S+S-〉 and the corresponding momentum distribution of the structure factorS+-(q)to characterize the HaldaneCand HaldaneICphases.The transversal spin correlations〈S+S-〉exhibit different decay forms in both subphases.The results show that the transversal spin structure factorS+-(q)exhibits an incommensurate oscillation pattern in the HaldaneIC.Our numerical method can provide a powerful tool for characterizing incommensurable phases.In addition, the transition pointαc(χ) between the HaldaneCand HaldaneICphases is detected by using von Neumann entropy.The singular values of second-order derivatives of the von Neumann entropy correspond to the transition pointsαc(χ).As a typical example of the SPT phase,[29–31]the Haldane phase is protected by any of the following three symmetries:bond-centered inversion symmetry, time-reversal symmetry,and a dihedral group comprising any pair ofπ-rotations in the spin space.[29,30]In order to further characterize the HaldaneCand HaldaneICphases, we also calculate the nonlocal order parameter.The nonlocal order parameter of the bond-centered inversion with a saturation value of-1 and the nonzero value string order indicate that the Haldane phase is a symmetryprotected topological phase.
In this study, the infinite matrix product state (iMPS)algorithm[32]is used to calculate the ground state wave function withχas the bond dimension.The remainder of this article is organized as follows.In Section 2, bipartite entanglement entropy and entanglement spectrum are calculated; a transition point is located between the HaldaneCand HaldaneICphases, corresponding to the AKLT point withα=1/3.In Section 3, we discuss the bond-centered inversion nonlocal order parameter.Section 4 discusses the string order parameter, and Section 5 characterizes the HaldaneCand HaldaneICphases using the transversal spin correlations〈S+S-〉 and the corresponding momentum distribution of the structure factorS+-(q).Finally, a summary is presented in Section 6.

Fig.1.(a)Bipartite entanglement entropy S(χ)as a function of the parameter α with bond dimensions χ=30,60,120,150,and 200.(b)The second-order derivatives of the entanglement entropy S(χ)as a function of the parameter α.The bond dimension is χ =150.
2.Bipartite entanglement entropy and entanglement spectrum
The von Neumann entropy is a measure of bipartite entanglement for a quantum state,which is exploited to detect a transition point.This entropy is from the perspective of quantum information on the study phase transition.For a system of a pure state partitioned into two subsystems A and B,the bipartite entanglement entropy is defined asS=-TrρAlogρA=-TrρBlogρB, whereρA=|ψA〉〈ψA| (ρB=|ψB〉〈ψB|) denotes the reduced density matrix of subsystem A (B).In this study,we obtain the ground state wave function|ψ〉using the iMPS algorithm[32]from tensor network simulations.In the iMPS representation,the bipartite entanglement entropy for a semi-infinite chain may be rewritten as follows:
whereλdenotes the Schmidt decomposition coefficient, andχdenotes the bond dimension.Because we consider that the translation of two lattice points is invariant,entanglement entropyS(χ)=(Sa+Sb)/2.The bipartite entanglement entropyS(χ) is plotted in Fig.1(a) as a function of the parameterαwith the bond dimensionsχ= 30, 60, 120,150,and 200.In the region-1.5≤α ≤1.5, three phase transition points are located atα=-1,1/3,1 from the entanglement entropy,and they correspond to four phases: the dimerized phase,HaldaneCphase,HaldaneICphase,and trimerized phase.Notably, an antiferromagnetic phase occurs between the dimerized phase and HaldaneCphases, which disappears as the bond dimensionχincreases.In this study, we focus on the Haldane phase.To detect the transition pointαc(χ)between the HaldaneCand HaldaneICphases,we plot the secondorder derivatives of the entanglement entropyS(χ)as a function of the parameterαin Fig.1(b),with the bond dimensionχ=150.A singular point appears at theα=0.334,which is very close to the AKLT pointα=1/3.Our results indicate a transition at the AKLT point.
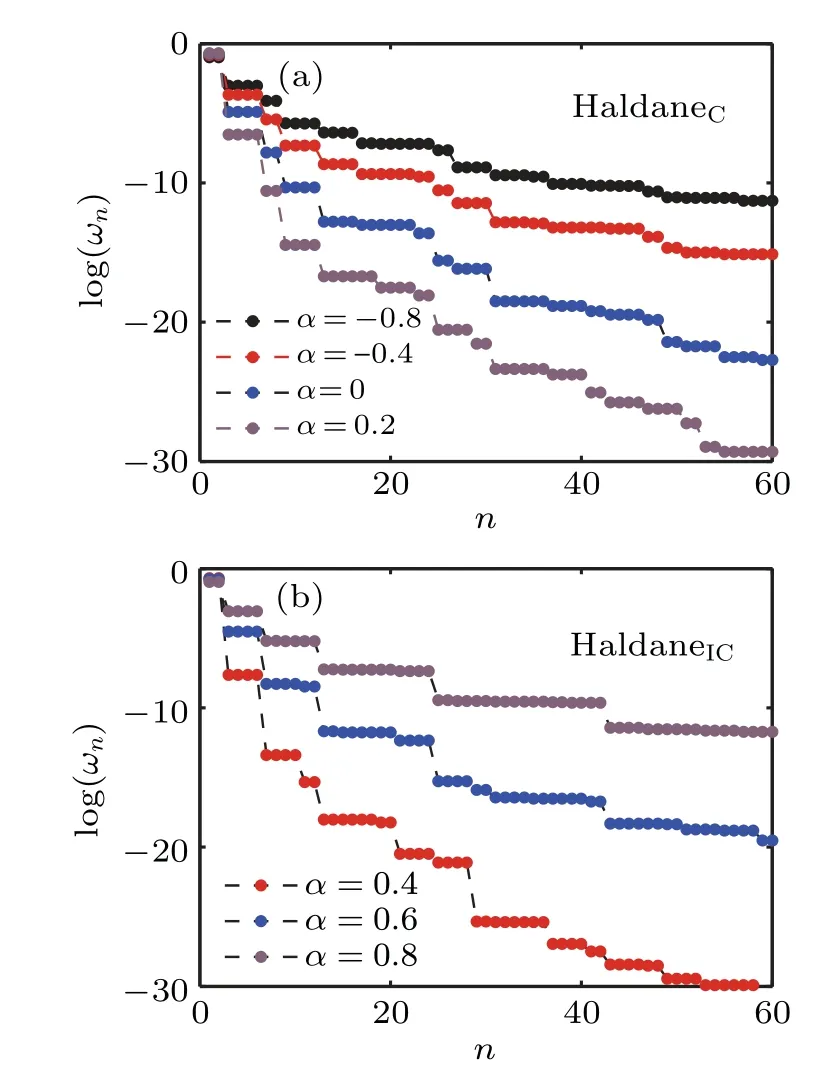
Fig.2.Entanglement spectrum En as a function of n for(a)HaldaneC phase and (b) HaldaneIC phase for different α parameters.The number of dots on each level indicates its degeneracy.The bond dimension χ =200.
The topological phases can be characterized by the entanglement spectrum.[33–36]The entanglement spectrum of a pure state of a bipartite system is the full set of eigenvalues of the reduced density matrix obtained from tracing out one part.In several cases, the spectrum contains additional information besides the entanglement entropy.In numerical studies,the entanglement spectrum is a robust tool for identifying topological phases.For a bipartite system, the entanglement spectrum[37]is defined as follows:
whereωn=denotes an eigenvalue of the reduced density matrixρ,nis the number of largest eigenvalues kept.In Fig.2,we plot the entanglement spectrumEnas a function ofnfor(a)the HaldaneCphase withα=-0.8,-0.4, 0, 0.2 and (b) the HaldaneICphase withα=0.4,0.6,0.8.Here,the bond dimensionχ=200.The results indicate that the entanglement spectrum shows double degeneracy in both phases.This means that the Haldane is a topological phase.But the entanglement spectrum can not distinguish the HaldaneCand HaldaneICphases.
3.The bond-centered inversion nonlocal order parameter
The Haldane phase[2]is a typical example of the SPT phase,[29–31]which is protected by any of the following three symmetries: bond-centered inversion symmetry,time-reversal symmetry, and a dihedral group comprising any pair ofπrotations in the spin space.[29,30]The topological phase cannot be characterized by a local order parameter, which falls beyond the Landau paradigm, but can be characterized by nonlocal order.The iMPS[32]and infinite density matrix renormalization group (iDMRG)[38]are robust tensor network algorithms, which can be exploited to efficiently simulate onedimensional quantum many-body systems.The algorithms generate a ground state wave function in an iMPS representation and provide an efficient means to evaluate various physical observables.From the iMPS simulation,the ground state|ψ〉is obtained, which is invariant under the two-site translation.In terms of the bond-centered inversionI(1,L),the bondcentered nonlocal order parameter for the segment comprisingLbonds of type A–B is defined as follows:[39,40]
whereλBdenotes the Schmidt decomposition coefficient,and the segment lengthLis even.A graphical representation is shown in Fig.3.

Fig.3.Graphical representation of nonlocal order parameters in the MPS picture for the segment comprising L bonds of type A–B.
We plot the nonlocal order parameterOas a function ofαwith the bond dimensionχ=200 in the Haldane phase in Fig.4(a).In the entire Haldane phase,Oreaches a saturation value of-1 whenαis away from the quantum phase points±1,indicating that the nonlocal order parameterOcannot distinguish between the HaldaneCand HaldaneICphases,but can be used to characterize the SPT phase.In addition, we plot the nonlocal order parameterOas a function of the segment lengthLwith the bond dimensionχ=200 forα=-0.4,0,0.4[Fig.4(b)].This indicates that the nonlocal order parameterOtends to a saturation value of-1 as the segment lengthLincreases.

Fig.4.(a)Nonlocal order parameter O as a function of α with the bond dimension χ=200 in the Haldane phase.(b)Saturation of the nonlocal order parameter O,with the block size L being even,for α =-0.4,0,0.4.
4.String order parameter
In the Haldane phase for the spin-1 BLBQ model with-1<α <1,due to the hiddenZ2×Z2symmetry is broken,[41]the characteristic order can be measured by the string correlation function[42]
wherer=|i-j| denotes the lattice distance.In Fig.5, we plot the string correlation functiong(r) as a function of the lattice distancerfor (a) HaldaneCphase withα=-0.8,-0.4, 0, 0.2 and (b) HaldaneICphase withα=0.4, 0.6, 0.8.Here, the bond dimensionχ=200.For a small lattice distancer, theg(r) rapidly tends to a saturation value, indicating that the long-range order is evident.If we continue to increase the lattice distancer, the saturation value of string correlationg(r) stays at the limiting value.Forα=0, the spin-1 BLBQ model corresponds to the spin-1 antiferromagnetic Heisenberg model.Consequently,we compute the string correlation function, which shows a long-range order withg(∞) =-0.374324443, with the bond dimensionχ= 200.Our result agrees with the resultg(∞) =-0.374325096(2)from the iDMRG algorithm.[43]The behaviors of string correlation are the same in both the HaldaneCand HaldaneICphases.Note our results show that the entanglement spectrum,the bond-centered inversion nonlocal order parameter,and the string correlation cannot distinguish the HaldaneC–HaldaneICtransition,but they can clearly characterize the Haldane phase.
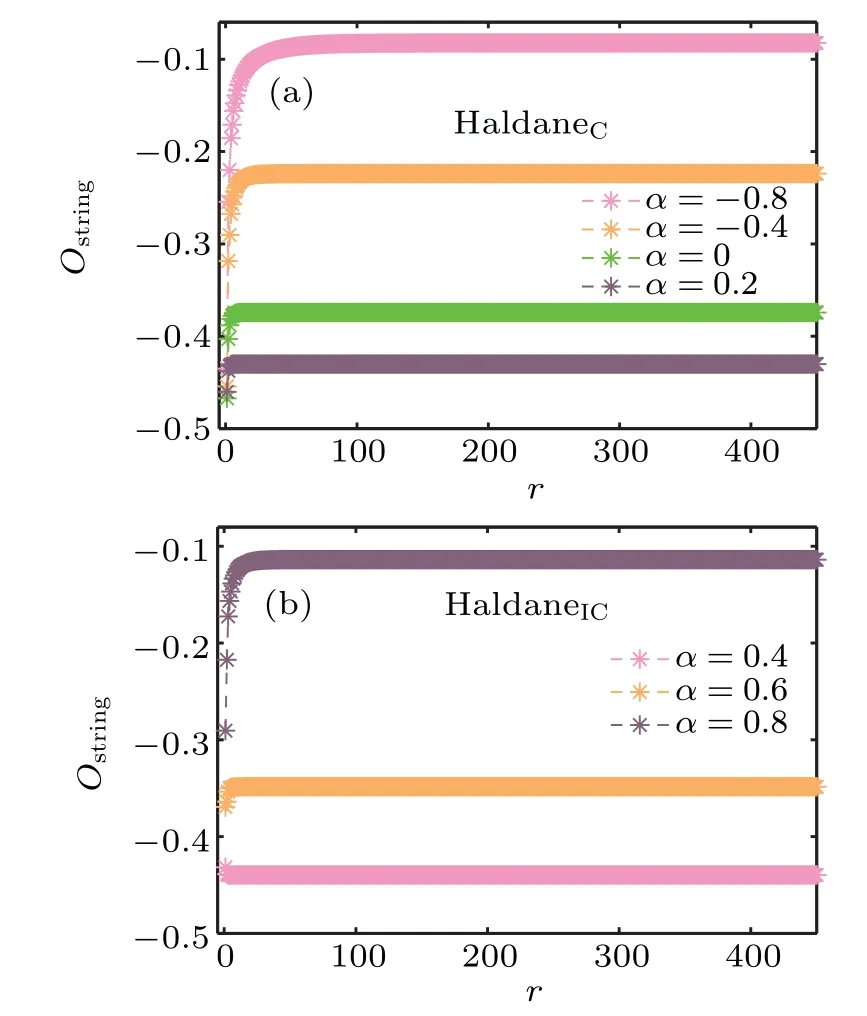
Fig.5.String correlation function g(r)as a function of the lattice distance r for(a)HaldaneC phase and(b)HaldaneIC phase for different α parameters.The bond dimension χ =200.
5.Characterization of the HaldaneC and HaldaneIC phases
We now characterize the HaldaneCand HaldaneICphases.Physically, “incommensurate” means the wavelength of the oscillation pattern is not an integer multiple of the lattice spacing.To characterize the HaldaneCand HaldaneICphases, we calculate the transversal spin correlationC(r)=with the spin operatorS±=Sx±iSy.By a Fourier transform, the static spin structure factor of the transversal spin correlation is defined as follows:[44–46]
In Fig.6(a), we plot the transversal spin correlationC(r) in the HaldaneCphase (up) withα=-0.8,-0.4, 0, 0.2 and the HaldaneICphase (down) withα= 0.4, 0.6, 0.8.The transversal spin correlation tends to zero as the lattice distancerincreases, indicating that no off-diagonal order exists in the Haldane phase.In addition, Fig.6(a) clearly shows that the transversal spin correlation〈〉 takes on different forms of decay in both HaldaneCand HaldaneICphases.To obtain the decay function,as an illustrative example,we choose two typical ground states in the HaldaneCand HaldaneICphases.In Fig.6(b) (up), for small lattice distancer=100, a number fit to the transversal spin correlation〈〉(for odd lattice distance) is performed withα=-0.8 in the HaldaneC,with the fitting functionC(r)=ar-η+b.The numerical constants are given asη=0.5118,a=0.69, andb=-0.0278.In Fig.6(b) (down), for the small lattice distancer=30, a number fit to the transversal spin correlation〈S+i S-j〉 is performed withα=0.6 in the HaldaneIC, with the fitting functionC(r)=r-ηcos(qr)+candq=βπ.The numerical constants are given asη=1.533,β=1.264, andc=-0.0012.The solid black line is the fit.Our results clearly show that the dominant decaying form to the transversal spin correlation is ∝r-ηfor the HaldaneCphase and ∝r-ηcos(qr) for the HaldaneICphase for small lattice distancer.In addition,to further characterize the HaldaneCand HaldaneICphases, we investigate the momentum distribution of the spin structure factorS+-(q).In Fig.6(c) (up), we plot the corresponding momentum distribution of the spin structure factorS+-(q)in the HaldaneCphase withα=-0.8,-0.4, 0, 0.2.For HaldaneCphase,we observe that the peaks for the transversal spin structure factorS+-(q)atq=±πare the uniform background.In Fig.6(c) (down), we plot the corresponding momentum distribution of the spin structure factorS+-(q)in the HaldaneICphase withα=0.4,0.6,0.8.For HaldaneICphase,we observe that the dips for the transversal spin structure factorS+-(q)are located atq=±π.In addition,we do see some peaks around(i)q=±0.7π,±1.3πforα=0.8, (ii)q=±0.66π,±1.34πforα=0.6 and(iii)q=±0.78π,±1.22πforα=0.4 in the transversal spin structure factorS+-(q),which account for the incommensurate contribution.Here, the bond dimension isχ=200.

Fig.6.(a) Transversal spin correlation C(r) in the HaldaneC phase (up) and the HaldaneIC phase (down) for various α parameters, (b) the fitting of the transversal correlation C(r)in the HaldaneC phase(up)with α =-0.8 and the HaldaneIC phase(down)with α =0.6,and(c)the corresponding momentum distribution of the structure factor S+-(q)in the HaldaneC phase(up)and the HaldaneIC phase(down)for various α parameters.The bond dimension χ =200.
As a result, the transversal spin correlation〈S+i S-j〉 exhibits different decay behaviors in HaldaneCand HaldaneICphases, respectively.The dominant decaying form of the transversal spin correlation〈S+i S-j〉is proportional tor-ηin the HaldaneCphase and is proportional tor-ηcos(qr) in the HaldaneICphase.In addition, the transversal spin structure factorS+-(q)exhibits an incommensurate oscillation pattern in the HaldaneIC.
6.Summary
The HaldaneCand HaldaneICphases for the spin-1 BLBQ model are investigated using the iMPS algorithm.A phase transition point, which corresponds to the AKLT point withα=1/3,is located by the bipartite entanglement entropy between the HaldaneCand HaldaneICphases.In both phases,the entanglement spectrum shows double degeneracy.We calculate the nonlocal order parameter of the bond-centered inversion in both phases,which rapidly approaches a saturation value of-1 as the segment lengthLincreases.The nonlocal string order is also calculated;a nonzero value string order can be used to characterize the topological phases.Forα=0,the spin-1 BLBQ model corresponds to the spin-1 antiferromagnetic Heisenberg model, and the string correlation function shows long-range order,withg(∞)~=-0.374325096(2)from the iDMRG algorithm.[43]Our results agree with the results from the iDMRG algorithm.[43]In addition,to distinguish the HaldaneCand HaldaneICphases, the transversal spin correlation〈S+i S-j〉 and corresponding momentum distribution of the structure factorS+-(q)are analyzed.Our results show that the dominant decaying form of the transversal spin correlation is proportional tor-ηfor HaldaneCphase and is proportional tor-ηcos(qr)for HaldaneICphase for a small lattice distancer.In addition, the HaldaneICphase exhibits an incommensurate oscillation pattern in the spin correlation structure factor.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No.11805285), the Natural Science Foundation of Shaanxi Province of China (Grant No.2022JM-033),and the Science and Technology Research Program of Chongqing Municipal Education Commission(Grant No.KJQN 201900703).
杂志排行
Chinese Physics B的其它文章
- Robustness of community networks against cascading failures with heterogeneous redistribution strategies
- Identifying multiple influential spreaders in complex networks based on spectral graph theory
- Self-similarity of complex networks under centrality-based node removal strategy
- Percolation transitions in edge-coupled interdependent networks with directed dependency links
- Important edge identification in complex networks based on local and global features
- Free running period affected by network structures of suprachiasmatic nucleus neurons exposed to constant light
