基于导频的OFDM 雷达通信一体化波形设计

李振华,姜 雪,朱炳祺

(1.上海交通大学电子信息与电气工程学院,上海 200240;2.上海无线电设备研究所,上海 201109)

0 引言

随着科技的发展进步,雷达与通信的一体化越来越受到不同领域研究人员的关注。在军事领域,为了增强作战能力,作战平台往往朝着小型化和多样化的方向发展[1],力求在尽可能小的平台上配备多样的电子作战设备,这导致不同系统之间的电磁干扰加剧,而雷达通信一体化是降低系统间干扰的有效途径。在民用领域,智能交通、智能车载网络等技术正蓬勃发展[2],未来的自动驾驶不仅需要快速探测周围环境,还需要连接互联网获取地图、道路拥堵情况等信息,因而雷达通信一体化是民用交通等领域技术发展的必然趋势。此外,由于频谱资源日益稀缺,雷达与通信频段开始有部分重叠[3]。这一系列因素都为雷达通信一体化的研究推进创造了条件。

雷达通信一体化的关键是实现共享信号的波形设计。现有的共享信号波形设计方向大体可以归纳为两类[4]:一是波形复用,二是波形融合。波形复用可以分为频分复用、时分复用、码分复用和空分复用等,但无论是哪种复用方式,都不可避免地存在资源利用不充分的问题。而波形融合则能够在确保良好通信和探测性能的前提下,最大化利用频谱资源。波形融合一般采用两种方法:一种是将通信信息调制到雷达信号上实现信号的一体化,例如将最小频移键控(MSK)信号调制到线性调频(LFM)信号上,形成融合波形[5];另一种是采用通信信号实现雷达探测功能,这种实现方式多采用正交频分复用(OFDM)信号。OFDM信号具有频谱利用率高、抗多径衰落、易于均衡等特点,在通信领域被广泛使用。近年来,OFDM信号的低旁瓣、距离-多普勒解耦、大时间带宽积等优点[6]被发掘,OFDM 雷达的研究也逐渐受到关注,这为基于OFDM 信号的雷达通信一体化的实现提供了可能。

目前在基于OFDM 的雷达通信一体化信号中,相位编码OFDM 信号受到广大学者的青睐。但是大多数研究都是从雷达的角度出发,直接将所有的通信信号都映射成相位编码信号后再传输,没有充分利用通信信号中的导频(pilot)序列来进行雷达探测,这在一定程度上降低了通信系统携带信息的能力。另外,一般的相位编码序列,如m 序列、巴克(Barker)码序列等形式较为固定,容易被截获。而混沌编码序列因具有初值敏感等特点,使其不仅相关性好,而且抗截获及抗干扰能力也较强。

本文基于导频实现雷达通信信号的一体化,在基本不降低通信码元速率的基础上实现雷达探测功能。采用相位编码混沌序列作为导频内的调制符号,利用相位编码混沌序列良好的自相关性能,通过自相关处理提取出导频的位置,并将得到的导频信号进行匹配滤波和脉冲压缩处理,从而实现目标检测。本文将通过仿真试验来验证该一体化信号设计方法的可行性。

1 一体化信号设计

传统的OFDM 雷达信号在每个脉冲中只传输一个OFDM 符号,该OFDM 信号模型s0(t)[7]可以描述为

式中:N 为一个OFDM 符号内包含的子载波数;a(n)在雷达信号中表示相位编码信号,而在通信信号中则表示传输的码元信息;fn=nΔf 为第n个子载波上的中心载波频率,其中Δf 为子载波间隔;rect(·)为矩形窗函数;TS为一个OFDM信号的符号周期。

若直接采用传统的OFDM 雷达信号形式作为雷达通信一体化信号波形,即一个雷达脉冲只发送一个OFDM 符号,则会存在通信速率低的问题。针对该问题,一般的解决方案是在一个雷达脉冲内连续发送多个OFDM 符号,则相应的一体化信号模型s1(t)可以描述为

式中:M 为一个雷达脉冲中包含的OFDM 符号个数;a(m,n)为第m 个OFDM 符号的第n 个子载波中调制的码元信息。基于多个OFDM 符号的一体化信号时频关系如图1所示。

图1 基于多个OFDM 符号的一体化信号时频图

因实际传输的通信信号一般在时间上有一定的相关性,通信信号的互相关较强,如雷达采用该信号进行探测,将会出现模糊问题。为了改善信号的探测性能,一般会在子载波调制之前将a(m,n)映射成一个伪随机序列来改善信号的互相关性能。比较常用的伪随机序列包括m 序列、Gold码序列等。但从图1可以看出,如每个子载波对应一个伪随机序列,当传输通信码元信息时,一个伪随机序列只能对应于一个码元,使得该一体化信号携带通信信息的能力降低为同等条件下传统通信信号的1/m,这将对高速通信性能造成较大的影响。为了在保证雷达探测性能的同时尽可能不降低通信速率,考虑将通信系统中用于信道估计的导频序列同时用于实现雷达探测功能。改进的基于导频的一体化信号的时频关系如图2所示。图中,深色的部分为一体化信号的导频子载波,其余为正常调制通信码元的子载波。导频序列一般不承载通信信息,因此可以使用雷达信号通常采用的相位编码序列。该一体化信号方案通过复用通信信号中的导频序列,在基本不降低通信码元速率的前提下,同时保证了雷达探测性能。但由于此时的一体化信号仅有部分子载波用于雷达探测,相比于一般全部子载波都用于探测的传统雷达信号而言,会存在距离估计精度下降以及距离估计最大范围受限的问题,即该一体化信号是牺牲了一定的雷达探测性能换取通信性能的折衷。

图2 改进的基于导频的一体化信号时频图

考虑雷达在一个相干处理时间内共发射K个雷达脉冲的情况。根据式(2),一个相干处理时间内的一体化信号模型s(t)可以描述为

式中:a(k,m,n)为一个相干处理时间内的第k个雷达脉冲中第m 个OFDM 符号的第n 个子载波中调制的导频相位编码符号或通信码元信息;Tp为雷达脉冲重复间隔(CPI)。

2 混沌相位编码序列

为了改善雷达的探测性能,用于雷达探测的导频序列a(k,m,n)通常会预先映射成伪随机相位编码序列,常用的伪随机序列有m 序列、Barker码序列等。但是这些常用的序列都存在不足:m 序列虽然自相关特性良好,但是互相关特性不是很理想,并且由于生成序列时采用的是线性反馈逻辑,容易被拦截和破译;Barker码序列虽然自相关、互相关特性都较为良好,但是码长最长只有13位,随机序列的图样丰富度不够,同样容易被拦截和破译[8]。

因此,为了在保证相关特性的前提下提升雷达探测的抗干扰能力,本文摒弃常用的相位编码序列,改为采用混沌序列实现相位编码。

根据李-约克定理[9],混沌的本质特征大概可以总结为以下几个方面:

a) 初值敏感性,对一条混沌轨迹初值施加非常微小的扰动,将会导致在后续的序列迭代中产生大范围的偏差;

b) 非周期性,一条确定初值等条件的混沌轨迹在序列迭代中可以与某个前序时刻的轨迹无限接近,但不会总重复出现相同的轨迹;

c) 有界性,混沌序列在迭代的过程中,轨迹运动线始终处于一个有界的区域内。

在实际应用中,混沌序列普遍都是通过映射的方式来获得的。混沌信号经过映射后进行量化,以产生相应的混沌序列。常用的映射方式有Logistic 映射、改进型的 Logistic 映射、Chebyshev映射和Tent映射。

为了找到相关特性更好的混沌序列,对采用上述4种映射方式产生的混沌序列进行了性能比对。基本参数设置:序列初值均为0.48,Chebyshev映射取4阶,各个混沌映射方式的映射分形参数均取定义的最大值,映射后均为二值量化。4种混沌序列的自相关旁瓣峰值和互相关均值如表1所示。

表1 混沌序列的自相关旁瓣峰值和互相关均值

由表1可以看出,Chebyshev混沌序列的自相关旁瓣峰值和互相关均值相对来说都是较低的,具有较为优异的自相关和互相关性能。本文所提一体化信号中的导频调制的相位编码序列将采用由4 阶Chebyshev 混沌映射产生的混沌序列。

3 一体化信号的接收处理

OFDM 一体化信号中通信信号的解调过程,就是OFDM 通信信号调制的逆过程,与传统的OFDM 通信系统的解调并无太大差别,本文不再赘述。本文着重分析一体化信号中雷达信号的接收处理过程。

假设目标是一个可以看成点目标的散射体,不考虑目标的雷达散射截面积变化,并且假设信号入射到目标后只经过一次反射。由于一个CPI一般时间不长,目标在一个CPI内所处的位置与速度可以认为是不变的,则雷达接收信号解调后的基带模型r(t)[10]可以描述为

式中:τ=2(R-vt)/c为信号传播时延,其中R为目标到雷达的距离,v为目标速度,c为光速;fc为调制的载波频率。

设h为一个OFDM 符号内采样时刻的序号。在t=hT+mTs+kTp时刻对接收基带信号进行采样,得到其离散信号表达式为

式中:T为采样间隔。

在实际应用场景中,为了保证OFDM 一体化信号子载波间的正交性,通常要保证子载波频率间距Δf远大于最大多普勒频移fD,一般有Δf＞10fD[3]。因此,式(5)中由速度带来的最后一个指数分量的影响常常可以忽略不计。对式(5)的时域信号进行离散傅里叶变换(DFT),可以得到接收信号的频域表达式

由于导频序列具有良好的自相关性,所以即使事先不知道导频序列的图样,也能够从相关信号中检测出导频所处位置的子载波。将导频提取出来后,采用匹配滤波器对相同雷达脉冲中的导频进行脉冲压缩处理,得到的滤波结果可以表示为

式中:min(·)为取最小值函数;max(·)为取最大值函数;w∈[0,2M-2]为匹配滤波后的点数;pkn为第k个雷达脉冲中位于第n个子载波的导频符号的实际序号;hmf(·)为匹配滤波器的时域函数;Ωm(w,n)为沿着m轴的匹配滤波器输出。从式(7)可以看到,信号经过匹配滤波后,目标的距离和速度分别沿着n轴和k轴引入了线性相移,可以将相位信息提取出来,从而得到目标的距离和速度信息。

对匹配滤波后的信号沿着m轴进行峰值采样,获得沿m轴的最佳信号输出。输出结果可以看成一个Np×K维的信号矩阵(k,n),其中Np为导频的个数。为了从信号矩阵中提取出目标的距离信息,仅考虑在离散傅里叶逆变换(IDFT)中有变化的指数项,则沿着n轴对(k,n)进行IDFT 可以表示为

式中:(·)为沿着n轴的离散傅里叶逆变换函数。

从式(8)可以看出,信号矩阵经IDFT 后,n轴上的峰值将会在原信号指数和由IDFT 引入的指数相互抵消时出现,根据距离峰值处的索引ri,可以推导目标的距离

同理,对沿着n轴进行IDFT 后的信号矩阵再沿着k轴进行DFT,进一步提取速度信息。同样仅考虑变换影响的指数项,则对应的方程式为

式中:Fk(·)为沿着k轴的离散傅里叶变换函数。

与式(9)类似,当指数相互抵消时,k轴上将会出现峰值。考虑到载波频率fc远大于信号带宽,则fc+pknΔf≈fc,由速度峰值索引vi推得的速度信息

式(9)和式(11)分别给出了距离、速度与各自轴上的峰值索引的关系。根据两式中索引的系数,目标的距离分辨率ΔR和速度分辨率Δv可以表示为

式中:B为雷达带宽。可知,雷达探测的距离分辨率取决于雷达带宽B,速度分辨率在载波频率确定的情况下,取决于脉冲重复间隔Tp。

同理,雷达探测的最大无模糊距离Rmax和最大无模糊速度vmax可以表示为

4 仿真实验

4.1 仿真条件

对一体化信号进行仿真验证。参考目前智能交通领域常用的频段等系统参数[4,11],设置的仿真实验的关键参数如表2所示。

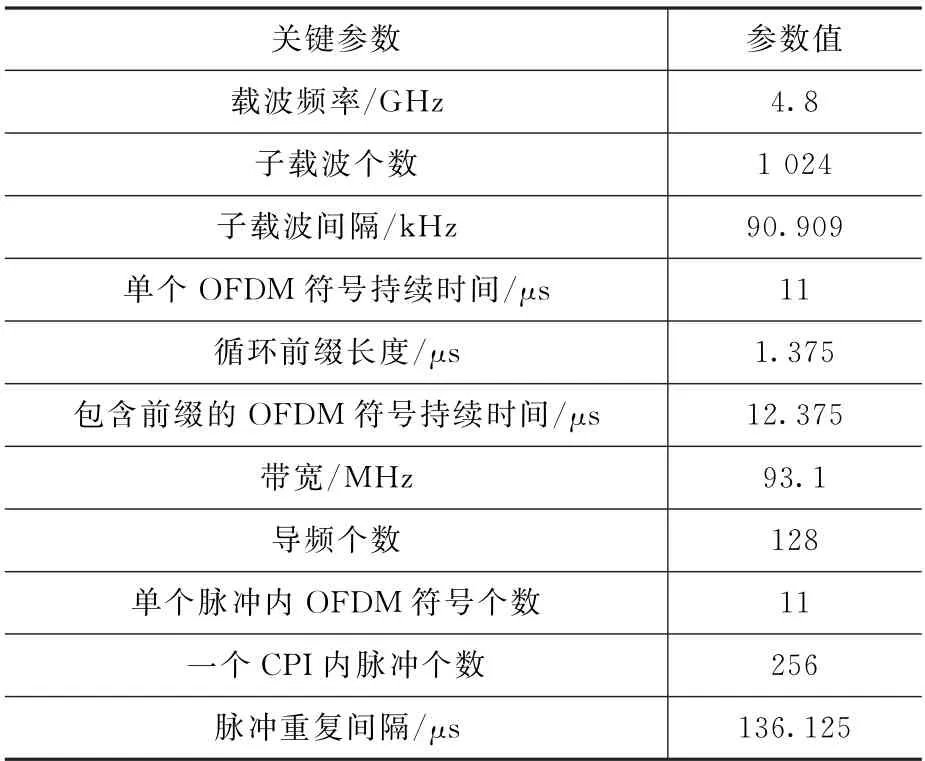
表2 仿真实验参数

4.2 雷达探测性能分析

雷达模糊函数是分析信号的雷达探测分辨率的重要工具。信号s1(t)的模糊函数χ(τ,fD)定义为

式中:*为共轭运算符。

按表2的参数值进行仿真,一体化信号的模糊函数的仿真结果如图3所示。

图3 一体化信号的模糊函数图

从图3可知,一体化信号的模糊函数图呈尖锐的图钉形状,旁瓣幅度远低于主瓣幅度,因而该一体化信号拥有良好的距离和速度分辨率。为分析模糊函数的性能指标,图4给出了一体化信号的零多普勒频率切面图和零时延切面图。

图4 一体化信号零多普勒频率和零时延切面图

由图4可知,零多普勒频率和零时延切面的归一化旁瓣最大幅度均没有超过0.2,更清晰地说明了一体化信号优良的距离和速度分辨性能。两个切面图都出现了一些细小的旁瓣针尖状峰值,这可能是由于每个导频上调制的是一样的混沌相位编码序列。

对一体化信号的目标探测性能也进行了仿真,系统仿真参数见表2。

根据雷达参数以及式(12),计算可得雷达的距离分辨率和速度分辨率分别为1.611 2 m 和0.896 8 m/s。

假设目标与雷达相距100 m,目标速度为50 m/s,得到的一体化信号的距离-速度二维联合估计结果如图5所示。探测估计得到的目标速度为50.218 1 m/s,目标距离为99.902 4 m,与实际目标的位置和速度信息基本一致。

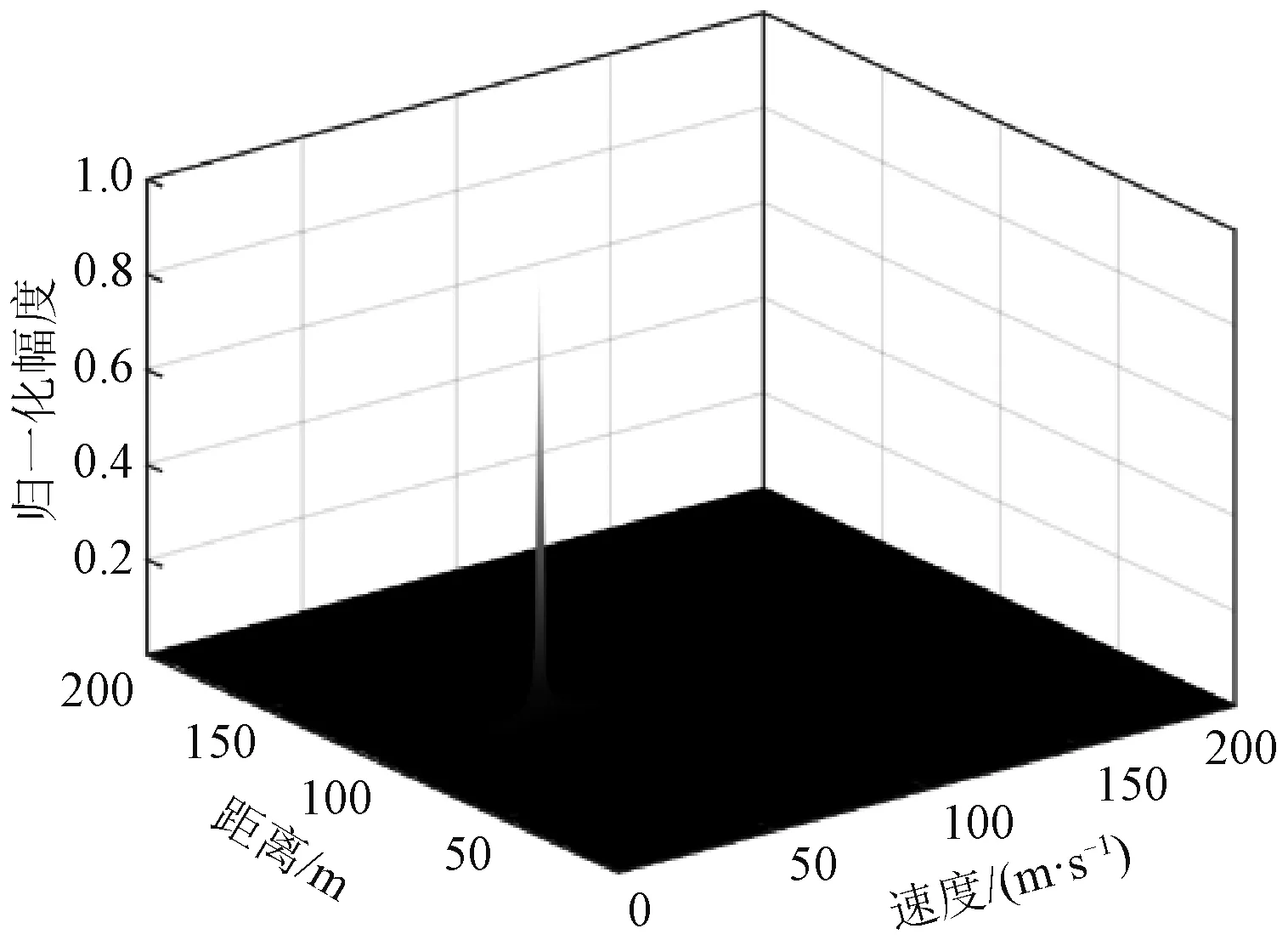
图5 一体化信号距离-速度二维联合估计

同时,为了进一步对比验证采用混沌序列的一体化信号在分辨率上的性能,在仿真实验中,将采用了Barker码序列的一体化信号作为对照组。从进行上述参数估计后的两种信号的三维图中截取速度-幅度、距离-幅度二维图,并将归一化幅度用对数形式表示,得到的速度和距离分辨性能对比曲线分别如图6和图7所示。可以看到,两种一体化信号的曲线大部分是在一个区间范围内重叠的,并且可以定量得到,基于混沌序列的一体化信号和基于Barker码序列的一体化信号的速度分辨性能曲线的旁瓣均值分别为-19.49dB 和-19.62dB,距离分辨性能曲线的旁瓣均值分别为-26.57dB。这说明,与基于Barker码序列的一体化信号相比,本文基于混沌序列的一体化信号的分辨性能曲线,仅旁瓣略有dB 和-26.95升高,分辨性能几乎可以认为是一致的。但由混沌序列的初值敏感特性带来的一体化信号的抗干扰性能以及低截获能力,则是Barker码序列无法实现的。

图7 距离分辨性能曲线

4.3 通信性能分析

根据表2给出的参数值,一体化信号中每个OFDM 符号有896 个调制通信信息的子载波。OFDM 调制方式采用4QAM (quadrature amplitude modulation)时,每个OFDM 符号可传输1 788 bit的通信信息,持续时间为12.375μs,则理想情况下的传输速率为144.5 Mbit/s,完全可满足大部分高速传输要求。

在加性高斯白噪声(AWGN)信道下,分别采用4QAM、16QAM、64QAM 等不同调制方式,对通信误码率进行仿真。最终得到的在不同调制方式下的一体化信号通信误码率的仿真结果如图8所示。

图8 一体化信号的通信误码率仿真曲线

从图8中可以看到,在多种调制方式下,一体化信号通信误码率的实验仿真值与理论值非常接近,说明了一体化信号的通信性能并不会由于雷达探测功能的加入而受到较大影响。

5 结论

本文提出了一种改进的OFDM 雷达通信一体化波形的设计方法,充分利用通信系统的导频序列进行雷达探测。根据导频良好的自相关性,分析推导了一体化信号中雷达信号的接收处理方法,在尽可能不影响通信速率的前提下,实现了雷达探测功能。同时,为了提高导频序列的随机性,本文通过引入混沌序列,利用混沌序列的初值敏感等特点,提升了雷达探测的抗截获与抗干扰能力。仿真结果证明,设计的一体化信号具有较高的雷达探测分辨率、较高的通信速率和较低的通信误码率。