榫连接结构微动疲劳寿命不确定性分析

2023-10-10张屹尚张嘉诚徐逸晗

兵器装备工程学报 2023年9期

陈实,张屹尚,张嘉诚,徐逸晗,孙凯

(1.中国航发商用航空发动机有限责任公司,上海 200241;2上海飞机发动机工程技术中心,上海 200241)

0 引言

榫连接结构是航空发动机叶片与轮盘连接的主要形式,在航空发动机飞行剖面转速工况下承受巨大的交变离心载荷,使得微动疲劳损伤成为其主要失效机制。而航空发动机全生命周期存在几何、载荷[1]、材料、监测误差等多种不确定性因素[2],这些因素导致发动机在试验、服役过程中性能偏离设计值,带来性能不达标甚至引发故障。因此针对榫连接结构微动疲劳寿命开展不确定性分析具有重要的意义。

蒙特卡洛法基于大数定律,适用于各种极限状态方程形式、变量维数、变量分布特征,广泛应用于航空发动机结构强度可靠性评估[3]。崔海涛等[4]以弹性模量、摩擦系数和寿命预测模型参数为随机变量,通过104次蒙特卡洛模拟,得到了不同可靠度下的燕尾榫结构微动疲劳寿命;同时,这一方法被用于燕尾榫结构高周微动疲劳寿命可靠性计算,然后基于Miner疲劳累积损伤准则,建立了高低周微动疲劳寿命对数正态分布模型[5]。此外,蒙特卡洛法也应用于航空发动机其他关键部件的研究,例如涡轮盘持久寿命分析[6],且蒙特卡洛抽样次数达到106。因此,对于高安全性要求的航空发动机限寿件失效风险评估问题,其失效属于小概率事件,传统蒙特卡洛方法在模拟时存在计算成本高、效率不足的问题。为此,工程上发展了基于抽样的传统蒙特卡洛模拟方法及其改进算法[7],与传统蒙特卡洛法计算时间成本相比,重要性抽样方法能够将时间降低约1个数量级。

目前,国内关于航空发动机榫连接结构微动疲劳寿命不确定性的研究相对较少。为此,本文中针对航空发动机榫连接结构微动疲劳寿命不确定性分析这一工程问题,提出了改进蒙特卡洛抽样方法,其应用贝塔分布抽样和双峰正态分布抽样对样本进行抽样,然后基于重要抽样思想推导得到变量原始分布特征的失效概率。结合非线性算例分析了分布参数、缩放参数和平移参数对改进蒙特卡洛抽样方法失效概率评估性能的影响。进一步地,针对航空发动机风扇叶片榫连接结构微动疲劳寿命不确定性分析问题,采用双峰正态分布抽样完成了失效概率计算及全局灵敏度分析。

1 改进蒙特卡洛抽样

蒙特卡洛法利用计算机生成服从变量空间随机分布的抽样样本,然后进行随机模拟试验,从而根据试验结果获得系统失效概率。设X=(X1,X2,…,Xn)为系统变量参数,其分布概率密度函数记为fX(X),功能函数记为g(x),则系统失效概率Pf可计算为

(1)

其中If[g(x)]为功能函数g(x)的指示函数,计算如下:

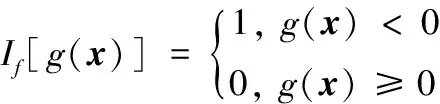
(2)

蒙特卡洛法借助计算机产生服从分布fX(x)的样本xi,然后模拟系统特性,则式(1)系统失效概率Pf的估计值为

(3)

从式(3)可知产生服从变量分布的随机样本为蒙特卡洛法以及改进的数字模拟方法的基础[8]。式(3)所示的简单随机抽样广泛应用于工程可靠性分析。但是在航空发动机零部件参数不确定性分析中,设计点变量通常为对应分布均值[1,10],属于小概率失效问题,简单随机抽样存在效率低、样本量巨大的问题。针对这一问题,研究人员提出了重要抽样法,其通过采用重要抽样密度函数代替变量分布密度函数,使得落入失效域的样本概率增加,从而提高失效概率预估精度和收敛速度[9]。在重要抽样法中,式(1)可计算为

(4)

式(4)中:hX(x)为重要抽样密度函数,此时失效概率估计值为:

(5)

式(5)中:xi不再服从变量分布概率密度函数fX(x),而是根据重要抽样密度函数hX(x)随机生成。

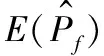
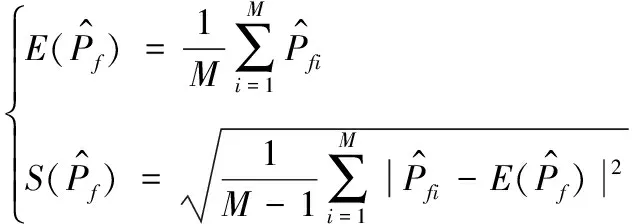
(6)

1.1 贝塔分布抽样

贝塔分布是一组定义在(0,1)区间的连续概率分布,其概率密度函数计算如下

(7)

式中:α、β为贝塔分布的2个参数,B(α,β)计算为

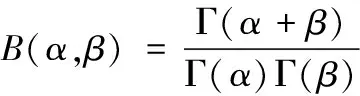
(8)

α、β均小于1时呈现中心概率密度小、边缘概率密度大的特点,均大于1时正相反,而均为1时则转化为均匀分布。

针对简单随机抽样在失效区域样本分布不足问题,将贝塔分布函数构造为重要抽样密度函数。引入缩放参数kB,将贝塔分布区间其扩增到目标变量区间,使抽样样本xi能够囊括失效区域,计算如下

(9)

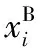
(10)

1.2 双峰正态分布抽样

双峰正态分布由2个正态分布叠加得到,其表达式为

(11)

式中:μ1、μ2、σ1、σ2分别为2个正态分布的均值和标准差,r为第一个正态分布所占的比重,本文取σ1=σ2=σ,r=0.5。抽样密度如图1所示。为了增加分布样本在失效区域的抽样概率,引入平移参数kD,使得

图1 双峰正态分布曲线

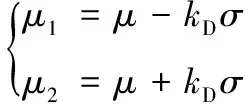
(12)

式中:μ为设计点,则式(11)为重要抽样密度函数hX(x)。

1.3 失效概率评估流程

失效概率评估流程包括固定抽样次数和依据收敛准则2种流程。前者按照抽样次数N直接进行随机模拟试验,然后根据试验结果评估失效概率。相比于简单随机抽样,重要抽样法在计算失效概率时考虑了抽样密度函数的影响。

按照收敛准则的失效概率评估流程如图2所示,收敛判据为前后两次预测失效概率的相对误差连续5次小于收敛指标。初始抽样次数为10,样本池样本为空集,按照抽样次数进行蒙特卡洛模拟,计算样本池的预测失效概率,当预测失效概率满足收敛指标时收敛次数加1;当预测失效概率不满足收敛指标时,收敛次数归零,然后按照抽样次数进行蒙特卡洛模拟,并将模拟样本放入样本池中,在样本池数目达到抽样次数的10倍时,则应更改抽样次数为样本池数目,如此往复,直至连续5次满足收敛指标后输出预测失效概率。

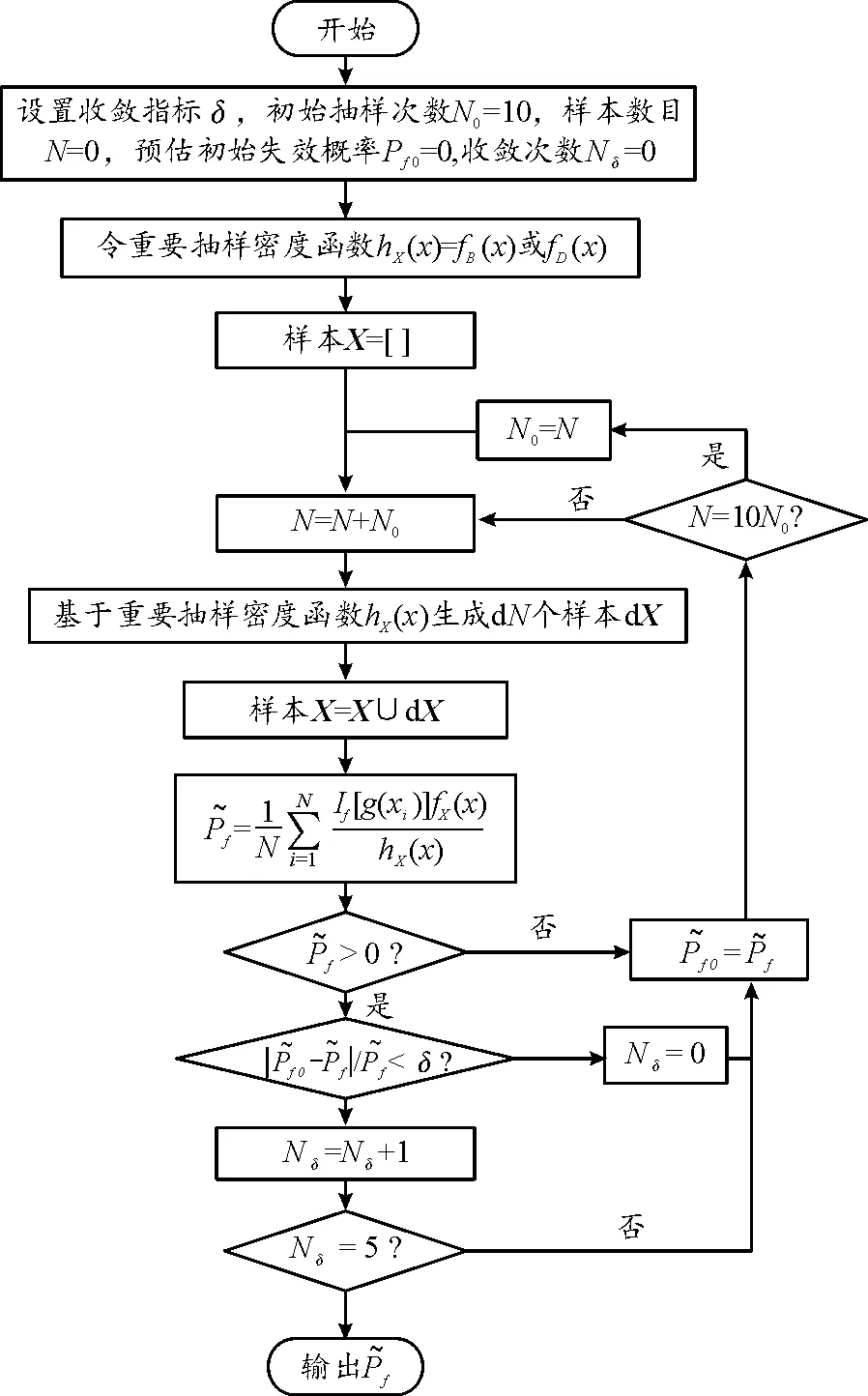
图2 依据收敛准则的失效概率评估流程

2 抽样性能分析

2.1 算例1

计算案例采用西北工业大学吕震宙等[8]提出的非线性功能函数,如下所示:

(13)

式中:X1、X2相互独立,且X1服从正态分布N(10,25),X2服从正态分布N(9.9,25),属于小概率失效。

针对上述功能函数,采用简单随机抽样、贝塔分布抽样和双峰正态分布抽样3种抽样方法,设置蒙特卡洛抽样次数分别为[10,102,103,104,105,106,107,108],开展100轮蒙特卡洛试验。

2.1.1简单随机抽样

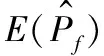
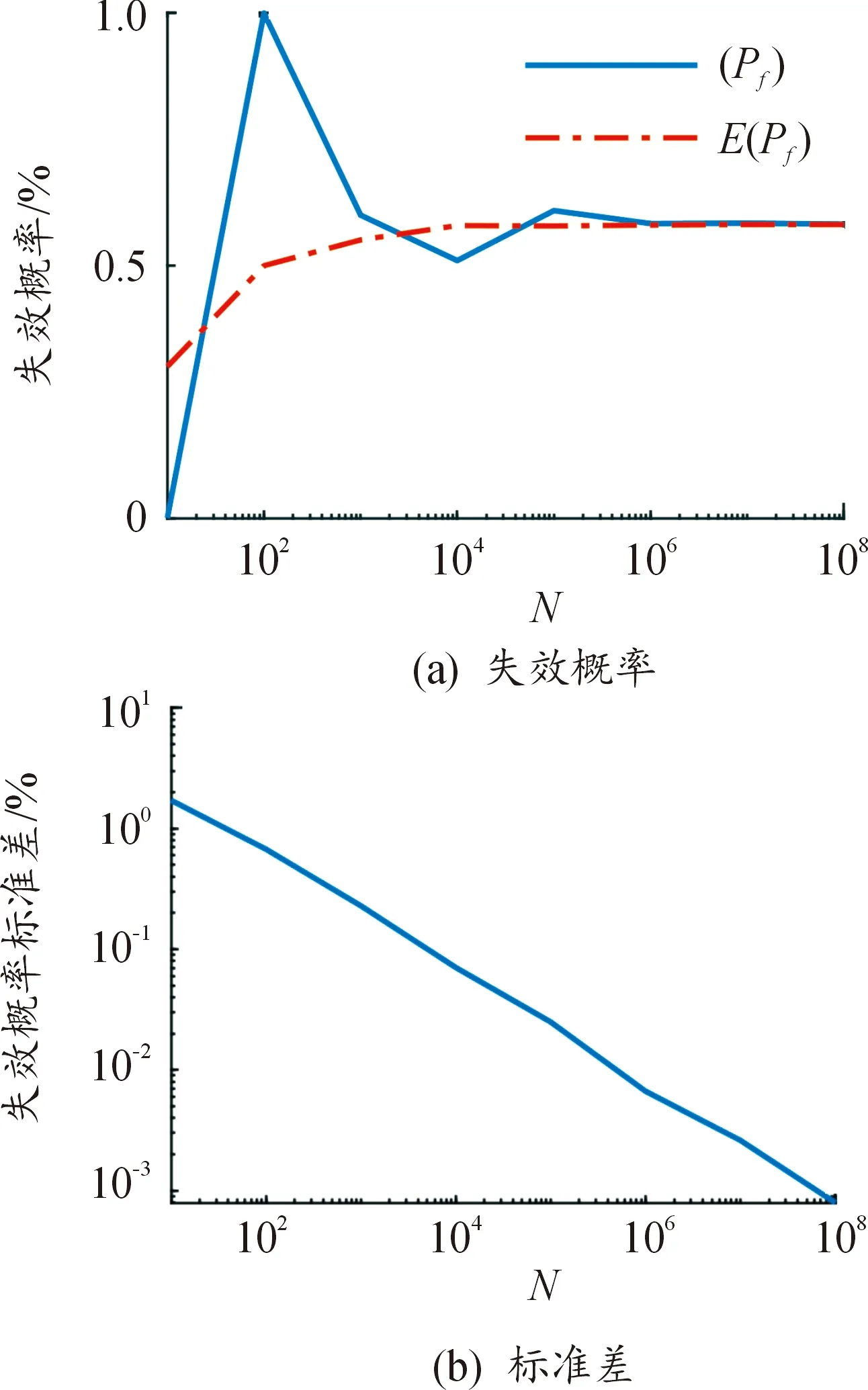
图3 简单随机抽样预测结果

2.1.2贝塔分布抽样

影响贝塔抽样密度函数及其失效概率评估的因素包括分布参数α、β以及缩放参数kB,通过随机模拟,分析这些参数对失效概率预估性能的影响。

1) 贝塔分布参数。设置缩放参数kB为8,对应样本分布范围为(μ-4σ,μ+4σ)。分布参数α=β且分别取值为0.75、1.00、1.25、1.50、1.75。如图4(a)所示,随着抽样次数的增加,不同分布参数的失效概率预估值均趋于稳定。在α=β=1.50时波动迅速减小并稳定在收敛值上,此时样本能够囊括绝大多数失效区域,且中心区域仍占有较多的样本,使得失效概率评估收敛较快。预估失效概率标准差如图4(b)所示,α=β=1.50情况下预估失效概率标准差在不同抽样次数下均处于较低水平。

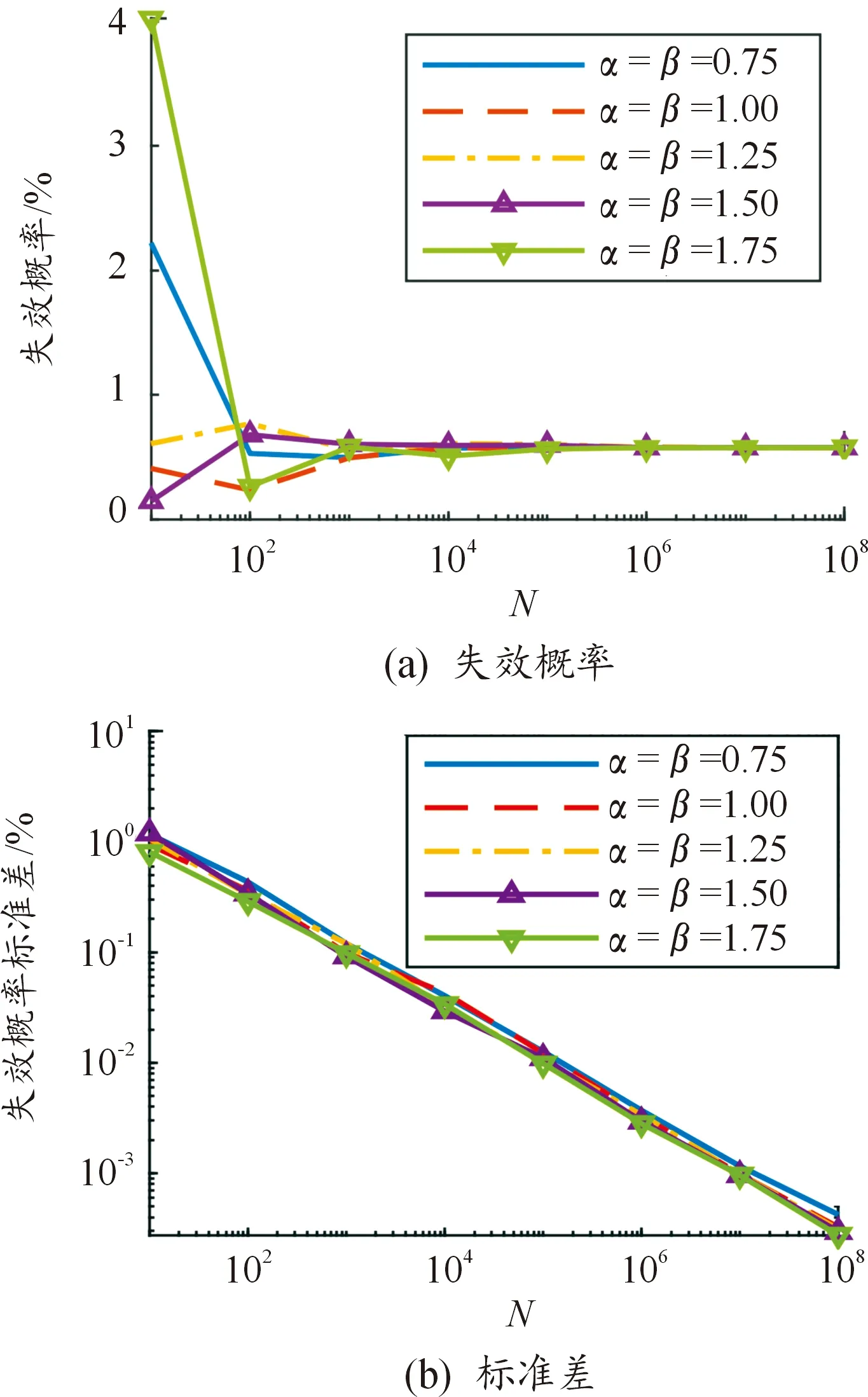
图4 不同分布参数下贝塔分布抽样预测结果

2) 缩放参数。设置分布参数α=β=1.50,缩放参数kB分别取值6、8、10、12、14,不同抽样次数下的单轮预测失效概率如图5(a)所示。在kB取值为6时,由于模拟样本分布范围为(μ-3σ,μ+3σ),使得超出区域并没有样本,导致预估失效概率值低于准确值。如图5(b)所示,由于缩放参数增加导致其在概率密度较大的失效区域分布的样本量反而减少,使得预测失效概率标准差随缩放参数增加而增大,在取值为10时可以达到较好的收敛效果。

图5 不同缩放参数下贝塔分布抽样预测结果

2.1.3 双峰正态分布抽样

影响双峰正态分布抽样密度函数的因素为平移参数kD。如图6(a)所示,不同平移参数单轮抽样结果均在106时趋于稳定,图6(b)所示的标准差表明kD在取值为2.0时可以得到较好的收敛速度,此时2个正态分布的均值分别为μ-2σ和μ+2σ。预估失效概率的标准差并非随着平移参数kD的增加而单调递增或单调递减,这是因为当平移参数kD较小时其抽样落入失效区域的样本偏少,其预测失效概率标准差与简单随机抽样相似;而当平移参数kD较大时其抽样样本落入失效区域的概率增加,但是落入概率密度较大的失效区域的样本量减少,导致其标准差也会增加。

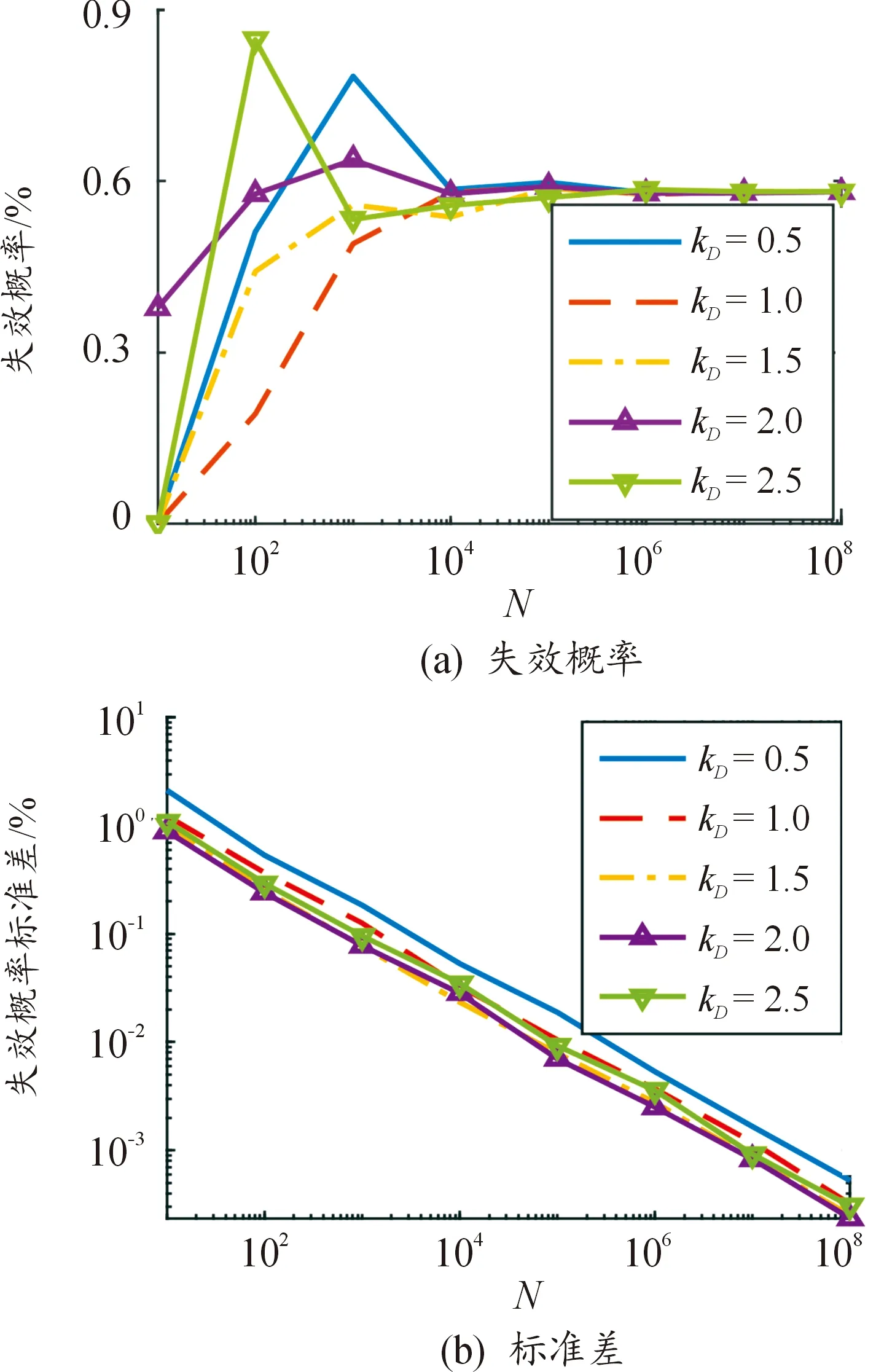
图6 不同平移参数下双峰正态分布抽样预测结果

2.1.4失效概率评估性能分析

设置贝塔分布参数α=β=1.50、kB=10,双峰正态分布参数kD=2.0,进一步对比三种抽样方法对失效概率预测性能的影响。1 000次随机抽样下不同抽样方式样本点的分布如图7所示,简单随机抽样只有极少数样本分布于非失效区域(黑色曲线左侧),贝塔分布抽样和双峰正态分布抽样样本分布较为均匀,从而能够提高失效概率预测精度。

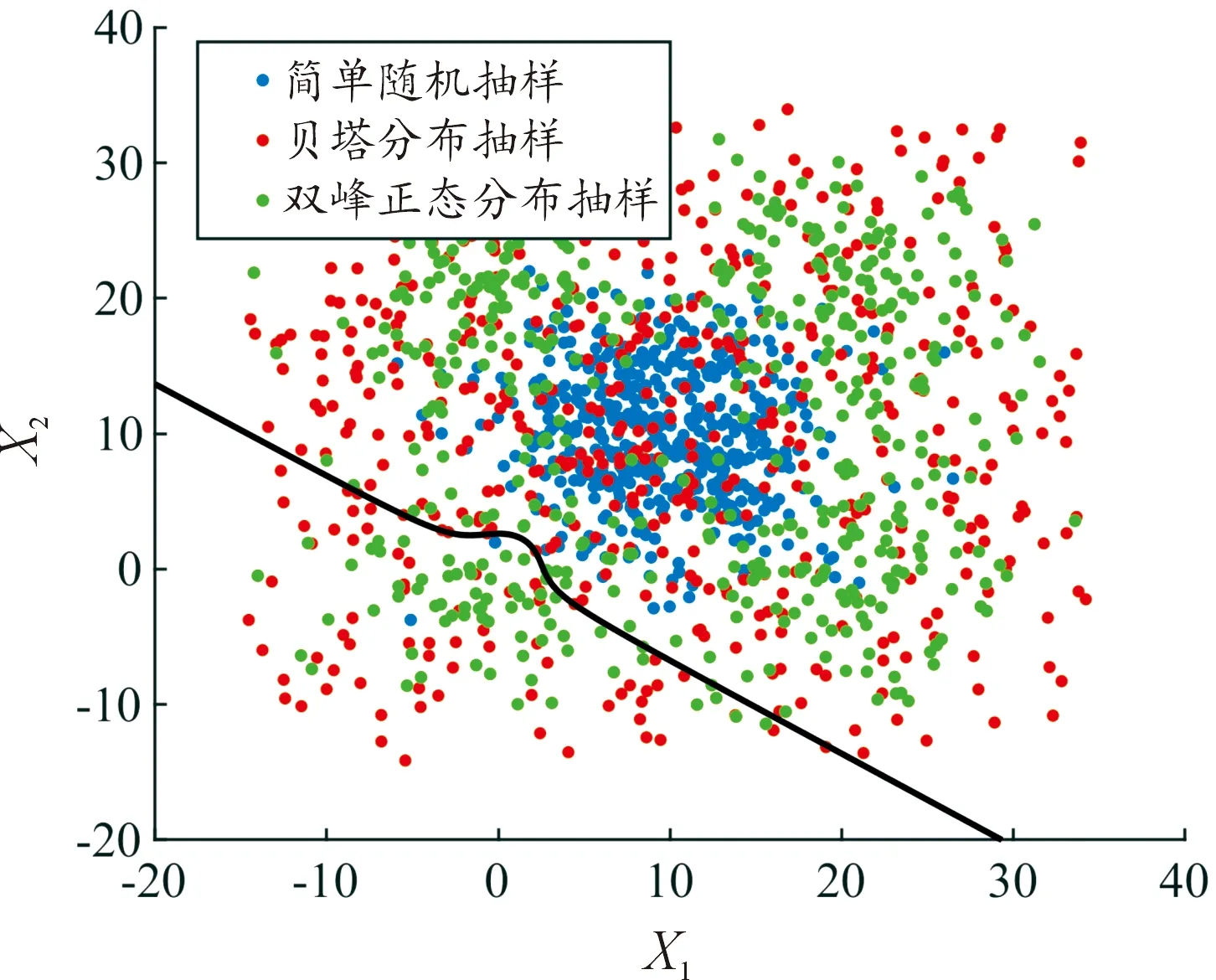
图7 不同抽样方式样本分布

如图8(a)所示,在抽样次数为10时,由于双峰正态分布和贝塔分布抽样样本点数目在失效和非失效区域分布量级一致,两者给出了与理论值量级一致的预测失效概率。另一方面,图8(b)为预测失效概率标准差相对于简单随机抽样的值,可以看出双峰正态分布失效概率预测标准差大约为简单随机抽样的一半甚至更少,证明其在收敛性能上要优于另外2种抽样方式。

图8 特定参数下不同抽样方法预测性能对比

按照图2流程,设置收敛指标δ为5%,进行10轮蒙特卡洛试验,不同抽样方式达到收敛所需的抽样次数如表1所示。取简单随机抽样108次预测失效概率期望值0.581 2%作为理论值,双峰正态分布抽样最为接近理论计算结果,其平均抽样次数不到简单随机抽样的1/10;而且简单随机抽样标准差最大,双峰正态分布抽样最小。

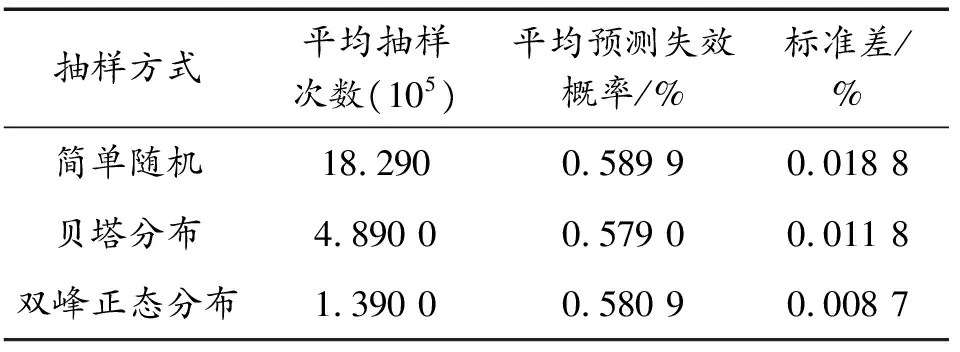
表1 不同抽样方法算例1预测结果对比

2.2 算例2

九盒段结构由64个杆元件和42个板元件构成,材料为铝合金,其2个主要失效模式的功能函数为[8]:

(14)

式中:R68、R77、R68为单元强度,外载荷P均值为120 kg,所有参数均满足正态分布,如表2所示。

表2 算例2计算参数

类似地,设置收敛指标δ为5%,进行10轮蒙特卡洛试验,其中贝塔分布参数α、β设置为1.5,缩放参数kB=10,双峰正态分布平移参数kD=2.0,3种抽样方法计算得到的结果如表3所示,双峰正态分布抽样达到收敛的平均次数为7.19×105,小于简单随机抽样和贝塔分布抽样,验证了改进蒙特卡洛抽样的准确性和高效性。

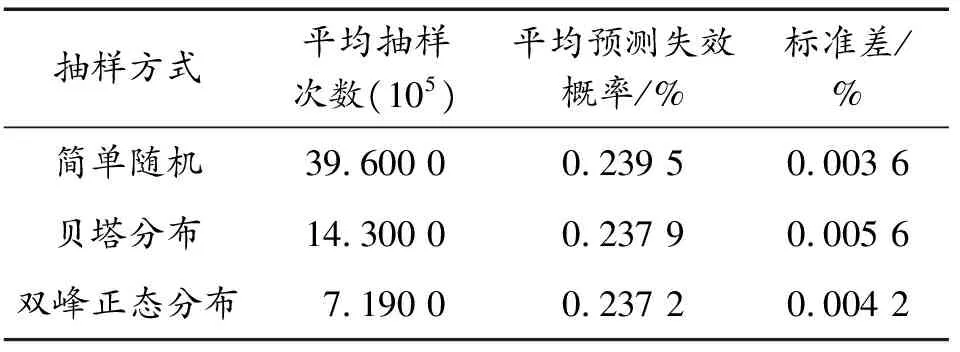
表3 不同抽样方法算例2预测结果对比

3 微动疲劳寿命不确定性分析

3.1 有限元模型

参考某型号风扇叶片、轮盘提取榫连接结构,简化为平面应力模型,如图9所示,榫头顶端施加风扇叶片离心载荷产生的压强P,榫槽两侧施加周向约束,榫槽底部施加全约束,设置接触区域摩擦系数为0.3。榫头、榫槽均采用TC4钛合金材料,如表4所示,参数均值来源于《中国航空材料手册》[11]TC4棒材室温下的低周疲劳数据,考虑随机因素为压强P和应变疲劳参数σ′f,假设两者均服从正态分布。

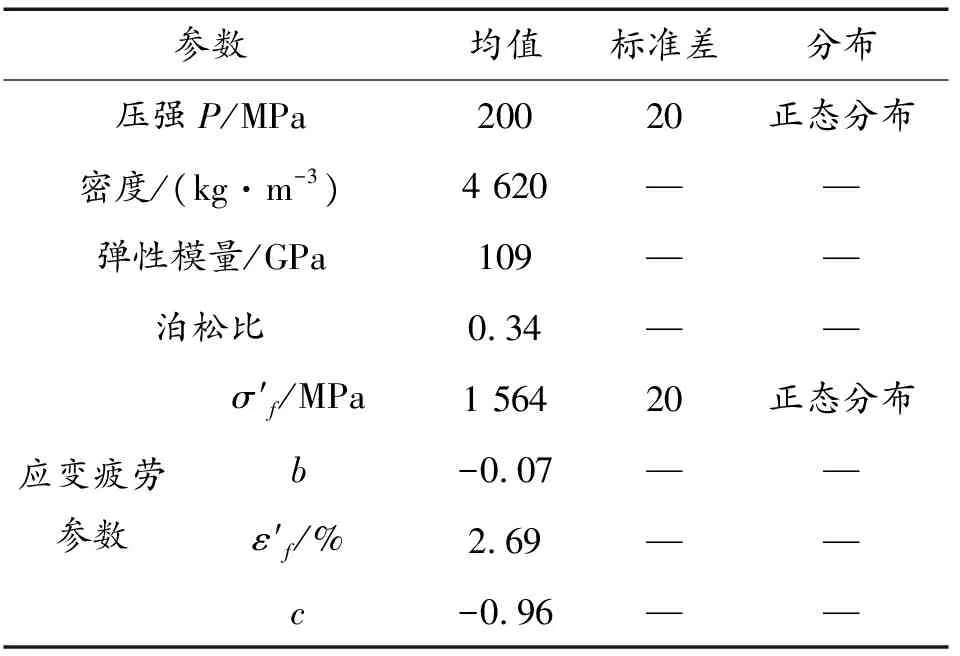
表4 榫连接结构计算参数

图9 榫连接结构有限元模型

取表4参数均值,计算结果如图10所示,接触区域应力分布与涡轮叶片榫连接结构[12]、枞树形榫连接结构[13]有限元计算结果相近,最大Mises应力均位于接触区边缘。

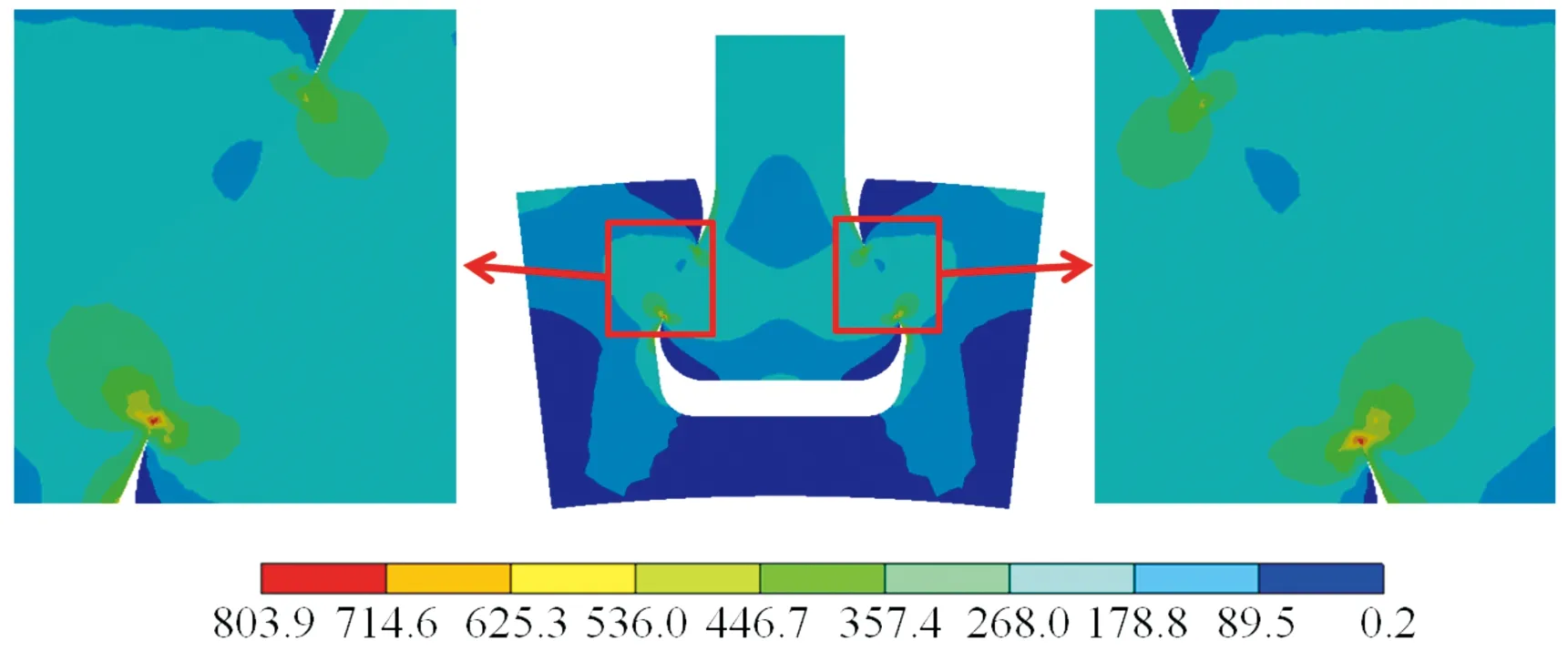
图10 榫连接结构应力分布

3.2 微动疲劳寿命计算

SWT损伤参量在钛合金燕尾榫连接结构微动疲劳预测方面具有较好的效果,该参量综合考虑了临界平面上的循环正应变幅εn,a和最大正应力σn,max为

SWT=σn,maxεn,a

(15)

其中临界平面为SWT值最大的平面,对应微动疲劳寿命为:

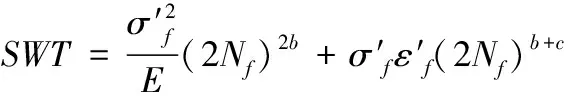
(16)

提取榫连接结构接触区域的应力和应变信息,计算各个节点的SWT损伤参量,如图11所示,在滑动区域两侧边缘存在2个SWT极值,与榫连接结构试验件计算结果一致[12]。将最大SWT值代入式(16)得到微动疲劳寿命为91 720,满足10 000周循环的寿命要求。

图11 接触区域损伤参量

3.3 微动疲劳寿命失效概率

考虑拉伸压强P和应变疲劳参数σ′f两个随机因素(表4),基于双峰正态分布抽样进行蒙特卡洛法模拟,计算榫头微动疲劳寿命失效概率。设定功能函数为

g(X)=Nf(X)-104

(17)

双峰正态分布抽样结果如图12所示,拉伸压强P的增加和材料应变疲劳参数σ′f的减少,都将导致榫连接结构微动疲劳寿命下降,甚至失效。对于同一个失效的样本点,相比于增加材料应变疲劳参数σ′f,改变更少的拉伸压强P就能满足寿命要求,如图12两个箭头所示。因此,降低转速波动更能有效降低结构失效概率。将抽样结果代入式(5)计算得到失效概率为0.046 4%。

3.4 失效概率影响因素分析

考虑拉伸压强P和应变疲劳参数σ′f的不确定性对榫连接结构失效概率的影响时,采用Cui等[14]提出的失效概率全局灵敏度指标,其表达式为

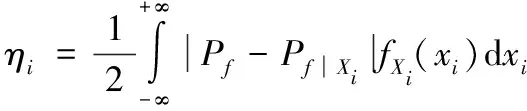
(18)

根据式(18)计算得到榫连接结构微动疲劳寿命失效概率影响因素的全局灵敏度指标如表5所示。拉伸压强P的全局灵敏度指标最大,说明其对榫连接结构微动疲劳寿命失效概率影响最为显著。这是因为拉伸压强P增大时将同时增加接触面的摩擦力和正压力,使得循环正应变幅εn,a和最大正应力σn,max增大,导致微动疲劳损伤参量SWT值迅速增加,且在同等标准差下拉伸压强P相对增加值更大,使得榫连接结构微动疲劳寿命迅速下降。因此,拉伸压强P,即转速波动对榫连接结构微动疲劳寿命影响不可忽略。