“多过程问题”的评价功能及其解决策略分析*——以2021年6月浙江选考物理第20题为例

何海卫 乐恩辉

(浙江省象山中学 浙江 宁波 315700)

物理学科学业水平考试的评价目的在于落实发展学生物理学科核心素养的课程目标.依据这样的目的,物理学业水平考试的命题必须时刻把握住学科核心素养的目标导向,在命题内容与情境创设上契合学生的认知水平,注重试题对“情境”“建模”“规律”“方法”等方面的定位与联系,加强对学生运用物理学知识综合解决实际问题能力的考查,强调创新精神与实践能力的考查,从而能较好地区分学生物理学科核心素养的水平[1].

浙江省物理选考卷在试题命制时已经就“情境”“建模”“规律”等维度实践探索多年并形成了相对成熟的形式.其中计算题第2题更是该类实践的典型代表,本题一般设置为“多过程问题”,通常以功能关系与动力学规律的运用为主线,以直线运动与曲线运动为主要的运动情境载体,通过信息解读、模型建构、数学方法渗透、科学论证等方面的综合运用,考查与评价学生运用物理规律与方法解决具体问题所具有的必备知识与关键能力.

为把握多过程计算题的考查要点,突破问题的难点,助力学生素养与能力的提升,本文基于《普通高中物理课程标准(2017年版2020年修订)》中高中物理选考命题的原则,对2021年6月浙江选考第20题的命题特点、评价功能进行简要评析,基于此并结合学生的认知基础提出优化此类问题解决策略的建议.

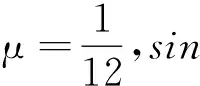
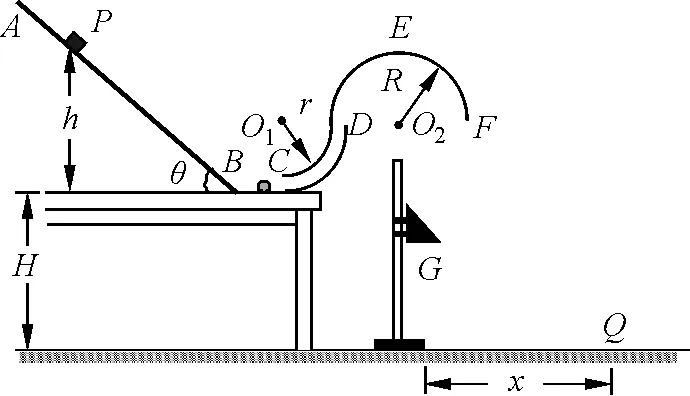
图1 题图

(1)若小滑块的初始高度h=0.9 m,求小滑块到达B点时速度v0的大小;

(2)若小球能完成整个运动过程,求h的最小值hmin;

(3)若小球恰好能过最高点E,且三棱柱G的位置上下可调,求落地点Q与F点的水平距离x的最大值xmax.

1 多过程问题的命题特征与评价功能

根据课程标准所制定的命题原则,多过程计算题依托具体的测试目标与任务情境,选择具有代表性的核心物理概念、规律、思想和方法等内容设计试题[1],聚焦核心知识,指向具体问题的解决.

1.1 基于测试目标与任务情境创设问题

以学生熟悉的高中物理常见的运动形式(匀变速直线运动、竖直平面内圆周运动、平抛运动等)为任务情境,以考查动力学规律与功能关系为测试目标,如表1所示,建立具有一定逻辑结构顺序与层次的问题载体,以此对学生的物理核心素养与处理综合性问题的能力展开考查.

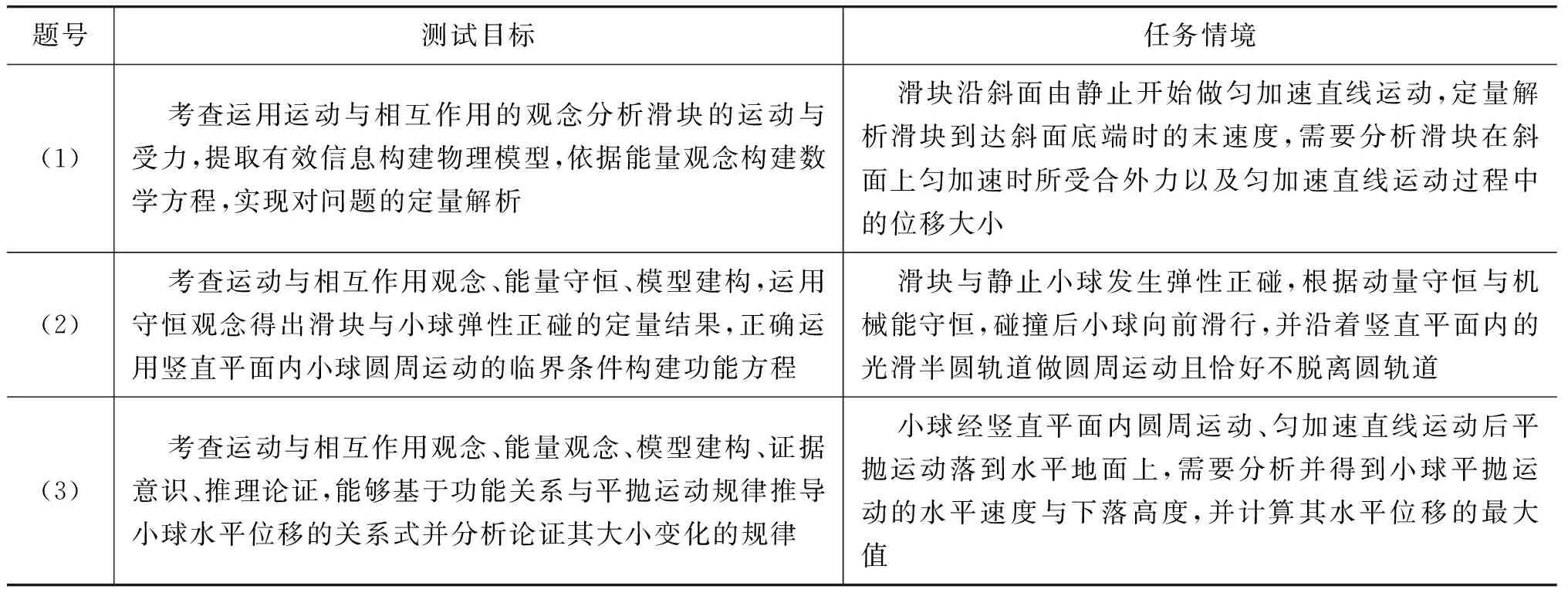
表1 测试目标与任务情境

1.2 聚焦功能关系与动力学规律解决问题

根据测试目标与任务情境解读问题的要素,关联用于问题解决的物理知识与方法(以功能关系与动力学规律所涉及的核心概念、模型建构、规律运用)为主要工具,注重考查学生对于答题逻辑结构的生成与建立,如表2所示.

表2 试题答案与问题解决的工具

1.3 基于学业质量水平评价物理学科素养的达成

多过程问题的命题多数是基于高中物理教学实践中所关联的运动情境、力学模型、功能转化的过程等核心要素,通过这些要素的内在联系与物理特征设计出指向分析物体运动、受力与功能关系的具体问题,并结合学业质量水平3、4相关指标与要求来评价学生在解决该问题的过程中其物理学科核心素养的达成情况[1],如表3所示.

表3 物理学业质量水平的达成情况

2 多过程问题的解决策略与优化

多过程问题涉及高中物理的动力学原理、问题解决的物理规律与方法、问题结论的数学分析与分类讨论等方面,综合性较强.解决该问题需要从冗长的题干中提取有效信息,并将所得信息关联到对应的知识点,从定性和定量两个方面对相关问题进行科学推理、找出规律、形成结论[2].在问题解决过程中要注重学生证据意识的培养,优化问题解决的策略与方法,从心理上逐步减弱学生面对综合性问题时的胆怯与回避心态,增强学生解决大题、难题的信心与勇气.

2.1 整体把握 创设问题解决的主线思路

分析问题思路不清晰往往是耽误学生解决多过程问题时间的主要因素.笔者在教学实践中对该题的分析思路总结为“信息获取→情境分析→模型建构→数学分析”4个环节,创建问题解决的科学思维过程,如图2所示,引导学生把握解决问题的正确思维方式,突破问题解决的要点与难点.

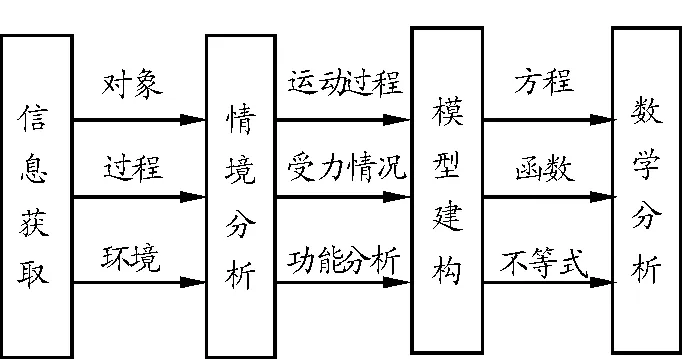
图2 解决多过程计算题的科学思维过程

(1)信息获取.研读题干内容,获取问题研究对象、过程以及对应条件要素所限定的物理环境.

(2)情境分析.根据所获取的题干信息明确物体的运动过程、各个过程中的受力分析,从而获取描述物体运动的物理量、所受合力大小与方向,并对整过程或者分过程的做功情况予以确定.

(3)模型建构.由运动、受力及做功情况明确构建相应的动力学模型,并根据动力学规律与功能关系构建用于定量解析问题的方程、函数或者不等式等.

(4)数学分析.对所建立的定量关系式进行分析与讨论,在基于问题物理本质的基础上运用数学方法获取科学规范的结论.

2.2 模型建构 明确过程分析的关键要素

模型建构是解决物理问题的关键要素,而过程分析则是进行模型建构的重要前提.对研究对象在运动过程中的运动形式、受力情况、做功与能量变化情况等要点(表4)有明确的认识与定位,能够充分助力解决问题所需物理模型的建构,并结合相关的物理规律实现对问题的定量解析.

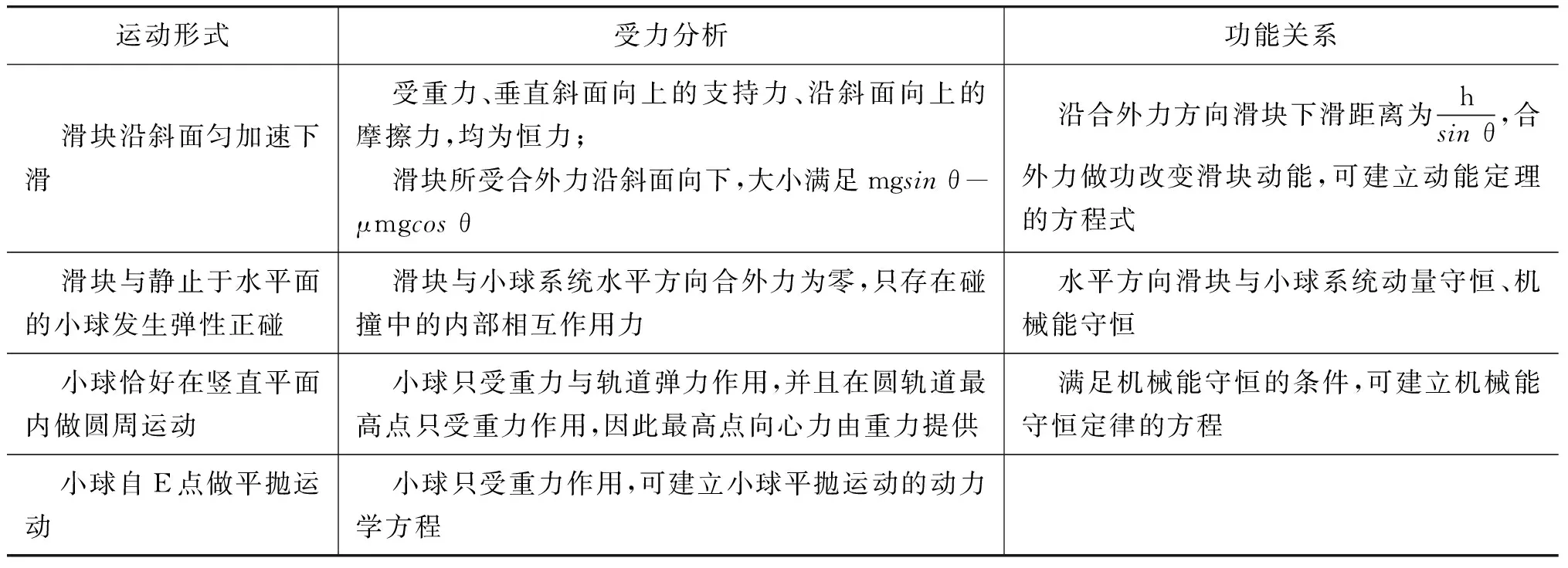
表4 过程分析的要点呈现

2.3 推理论证 生成科学客观的事实结论

多过程问题最大的难点在于构成运动的各个过程并不是独立的,而是相互关联的.因此对于单一运动过程的分析往往不能充分实现对问题的解决,而是需要对研究对象所参与的各个过程有整体的认识.因此在解决这样的问题时,不仅需要学生具备建构模型、分析计算的能力,还需要在对已有过程分析论证的基础上对新的问题进行预测、描述、解释,在基于规律运用与深化的基础上实现对研究问题的分析论证,从而获得严谨客观的事实结论.例如对该题第(3)问平抛运动水平位移最大值的求解可基于猜想预测、描述解释、推理论证的过程获取可靠的事实结论,如图3所示.

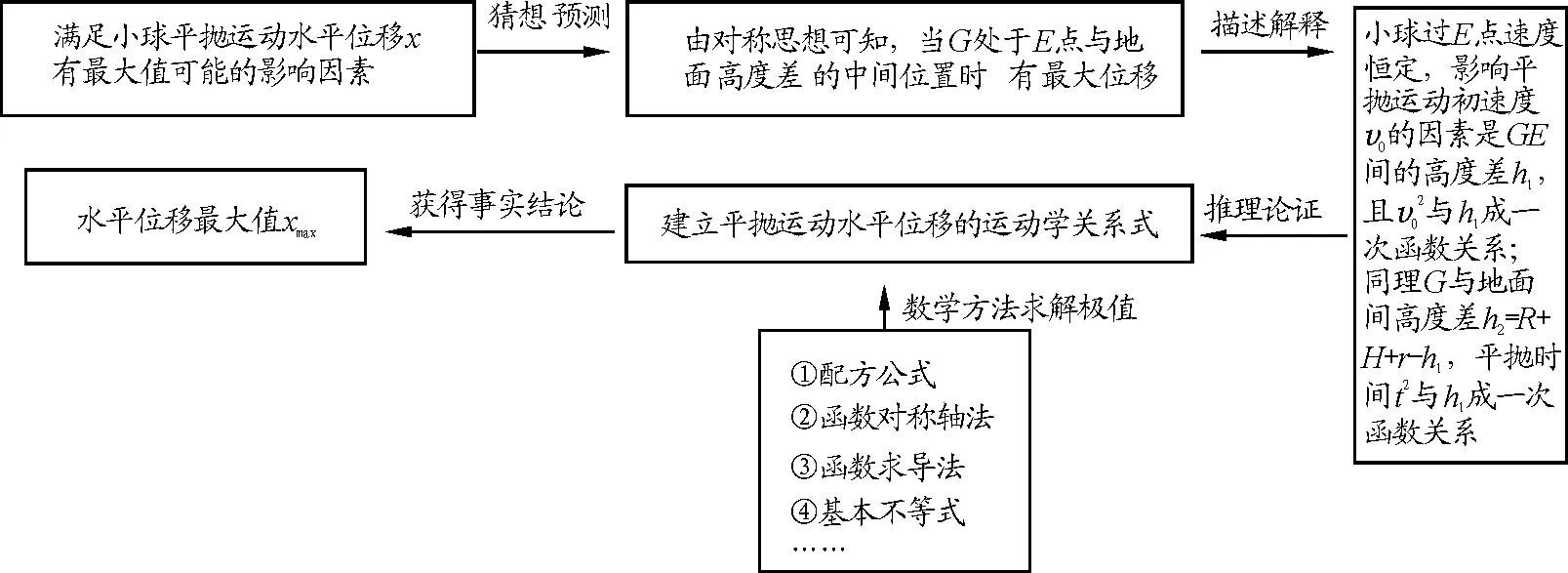
图3 问题解决的推理论证过程

3 结束语

多过程问题承载了高中阶段对学生综合能力水平与学科素养达成目标的考查要求,同时也是促进学生综合能力水平与学科素养发展的重要资源.在实际教学中,教师在把握该类问题在选考评价体系中的定位与导向的前提下,更要基于其评价功能充分发掘蕴含其中的概念、规律、方法等方面的资源要素,助力高中物理教学的提升与深化.