应用GeoGebra软件分析带电粒子在复合场中的运动

徐 雪

(贵州师范大学物理与电子科学学院 贵州 贵阳 550025)

随着课程标准的修订与高考评价体系的实施,高考命题的立意逐步发生改变,从知识引领到能力引领,从三维目标到核心素养,从物理知识到物理观念.在2022年高考全国甲卷理综第18题中设计了带电粒子从静止开始在匀强电场和匀强磁场中的运动,本文将借助该道例题的物理模型,应用GeoGebra软件对带电粒子在复合场中的运动展开研究.

1 GeoGebra软件介绍

GeoGebra软件是结合几何(geometry)和微积分(algebra)的动态数学软件,由美国佛罗里达州亚特兰大大学的数学教授 Markus Hohenwarter 开发,逐步从欧洲推广到各国,从数学应用到物理[1].GeoGebra功能齐全并易于操作,集几何、代数、表格、图形、统计、微积分于一体,软件界面有绘图区、指令区、代数区、工具栏、选项栏,如图1所示.绘图区制作图形,指令区输入代数表达式,代数区显示绘制图形的代数特征以及指令区输入的代数,工具栏提供作图工具.通过基本图形绘制出各种复杂模型,结合函数及数学方程可建立各种物理模型.笔者将借助GeoGebra软件研究带电粒子在复合场中的运动,弥补传统教学技术的不足,提高模型建构能力;弥补空间想象力的不足,提高理解能力;弥补抽象思维能力的不足,提高分析推理能力.

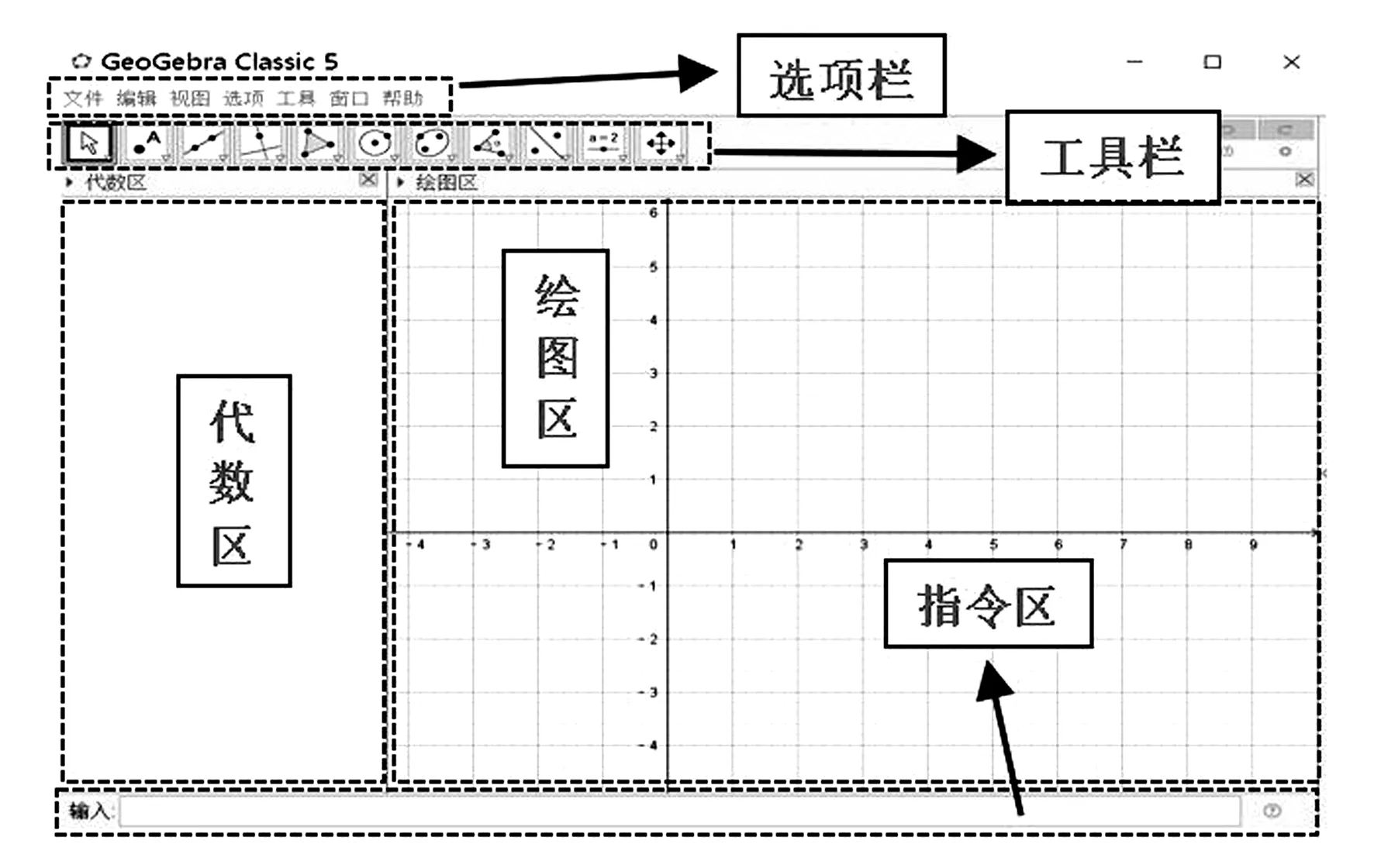
图1 GeoGebra的操作界面

2 GeoGebra软件应用

2.1 试题

【例1】(2022年高考全国甲卷理综第18题)空间存在着匀强磁场和匀强电场,磁场的方向垂直于纸面(xOy平面)向里,电场的方向沿y轴正方向.一带正电的粒子在电场和磁场的作用下,从坐标原点O由静止开始运动.下列4幅图中,可能正确描述该粒子运动轨迹的是( )

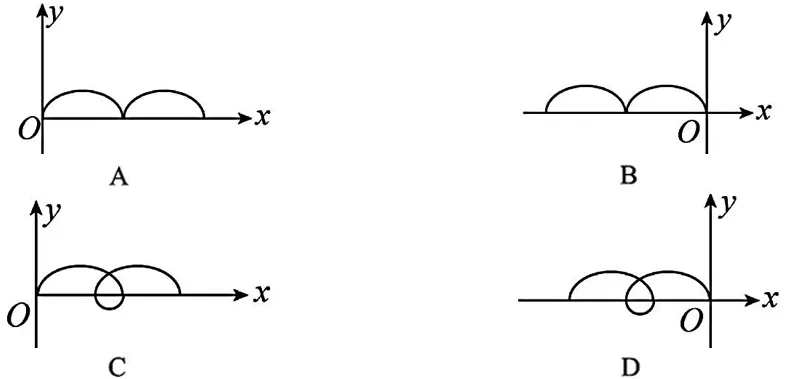
2.2 课件制作

2.2.1 模型制作原理

首先,分析带电粒子在复合场中的受力情况,不计重力的情况下,带电粒子在复合场中会同时受到洛伦兹力和电场力的作用.其次,结合动力学方程即牛顿第二定律微分方程,将粒子的受力情况与运动情况建立联系.最后,建立微分方程组,求得带电粒子的运动学方程,也就建立了该模型最核心的数学方程式[2].

设一带电粒子质量为m,带电荷量为q,在正交匀强电磁场中xOy平面上运动,磁感应强度为B,其方向垂直平面向外,电场强度为E,其方向沿y轴正方向.带电粒子的初始位置在坐标原点,用v0x和v0y分别表示带电粒子的初速度在x轴和y轴方向上的分量.求出带电粒子在电磁场中的运动方程.

解析：带电粒子受到的电场力为

F电=qE

受到的洛伦兹力为

F洛=qv×B

因此带电粒子在电磁场中的受力为

F=qE+qv×B=q(E+v×B)

根据牛顿第二定律

可得微分方程

当t=0时将初始条件

代入方程,微分方程组可解得

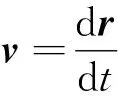
2.2.2 课件制作步骤

(1)设置参量数值.在指令栏中输入时间、质量、电荷量、磁感应强度、电场强度、初速度分量等各物理量的具体数值,并确定各物理量的取值范围.

(2)输入轨迹函数.确定带电粒子任意时刻的位置P,在指令栏中输入vx、vy随时间变化的速度方程,再输入x、y随时间变化的位置方程.此处需要注意运用If条件语句,以vx为例,输入:

cos(qBt/m)+v0ysin(qBt/m))

其含义为:如果B=0,则

vx(t)=v0x

否则

同理输入其余方程确定粒子运动的速度以及P的位置坐标.

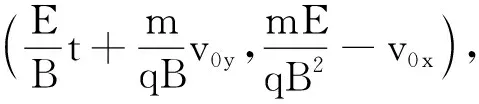
(4)确定其余点,画速度方向.以P点为参考点,找P1点和P2点坐标位置与P点坐标的关系,P1为[x(P)+vx(t),y(P)],P2为[x(P),y(P)+vy(t)],利用向量工具连接P与P1、P2得到x轴、y轴的速度分量.再由P1、P2坐标确定A坐标位置为(P1,P2),用向量工具连接P、A即为粒子合速度方向.

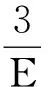
(6)改变参量,开启动画.开启对P点的跟踪,便可显示带电粒子在复合场中运动的轨迹,最后效果图如图2所示.

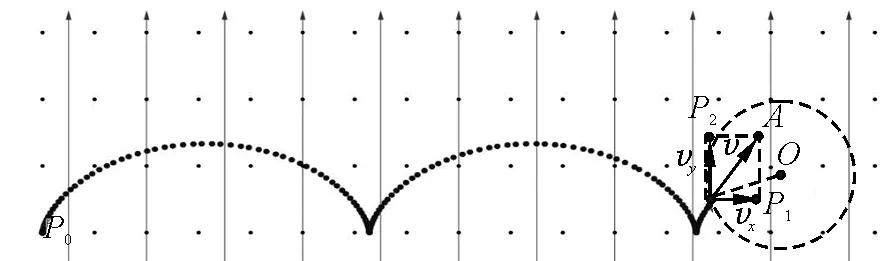
图2 带电粒子在复合场中的运动轨迹

2.3 带电粒子在复合场中运动的可视化

2.3.1 单个粒子运动轨迹的可视化

以2022年高考全国甲卷理综第18题为例进行操作演示.磁场方向垂直纸面向里,与所预设条件相反,故B为负值;电场方向沿y轴正方向,与预设条件相同,故E为正值.带正电的粒子由静止开始运动,电荷量q为正值,初始速度为零,即沿坐标轴上的速度分量都为零.随机改变B、m、E、q的大小,粒子运动轨迹都是一条摆线,如图3所示.通过控制变量,还可直观感受到磁场变大时,摆线幅度减小;电场变大时,摆线幅度增大.当改变电磁场的方向时,摆线所在的坐标象限会相应改变.一题变多题,一种情景变多种情景,不仅加深学生的理解和认知,而且学生从“听见”到“看见”的过程中能在头脑中主动建构物理模型,提高模型建构能力.

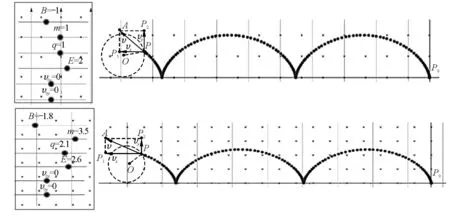
图3 改变参量前后的粒子运动轨迹

2.3.2 多个粒子运动轨迹的可视化

假设磁场方向垂直纸面向外,磁感应强度的大小B=1 T,电场沿y轴正方向,电场强度的大小E=2 N/C,粒子质量m=1 kg,电荷量q=1 C.当初速度不为零时,粒子的轨迹又将如何变化?

情况一:粒子沿x轴方向以初速度v0x射出,改变v0x的大小,观察粒子运动轨迹的变化.

(1)当粒子以一定初速度沿x轴正半轴射出,速度v0x的大小依次设为0.5、1、1.5、2、2.5、3、3.5、4等数值,其所对应的运动轨迹顺序依次为从上到下的短摆线,当v0x=4时,其所对应运动轨迹为最下面一条摆线,如图4所示.

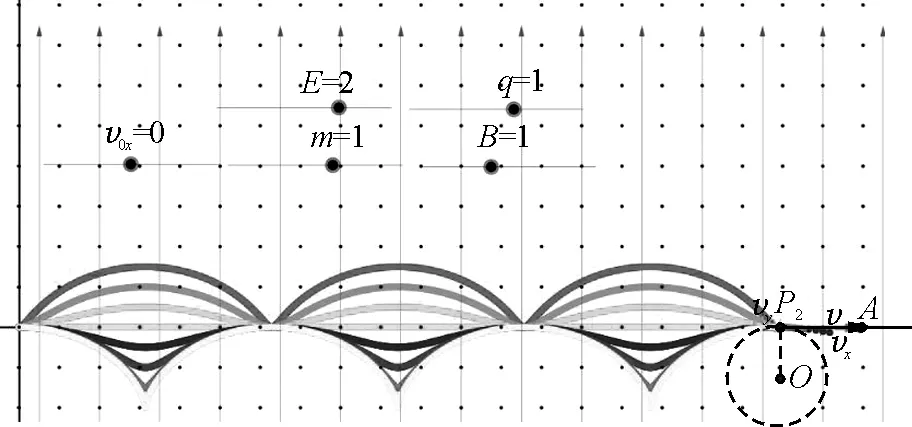
图4 粒子沿x轴正半轴射出的运动轨迹

(2)若再继续增大v0x的值分别为5、6、7、8、9、10,其所对应的运动轨迹顺序依次为由里到外的长摆线,如图5所示.

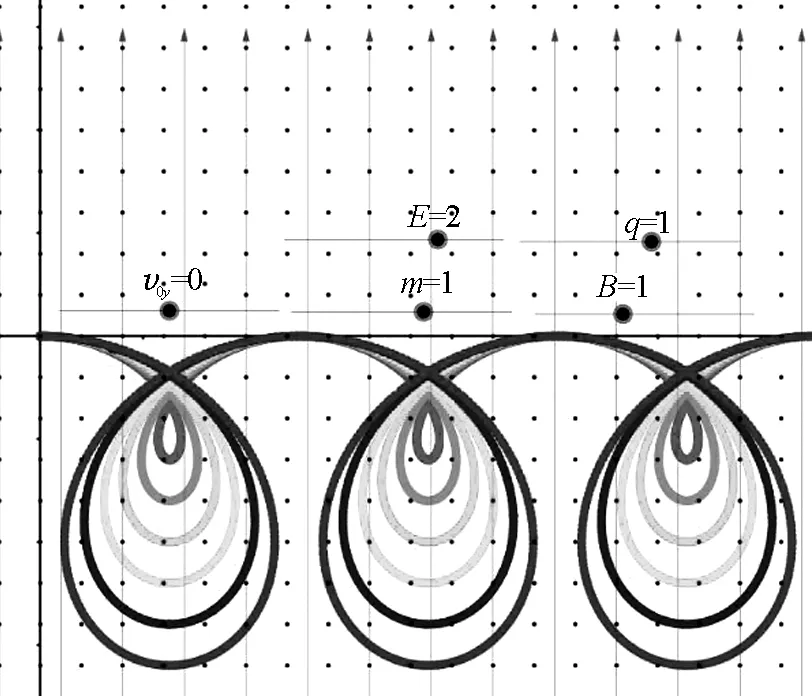
图5 粒子速度继续增大的运动轨迹

(3)若当粒子以一定初速度沿x轴负半轴射出,v0x的数值为别为1、2、3、4、5,则所对应的粒子运动的轨迹顺序依次是由下到上的长摆线,如图6所示.

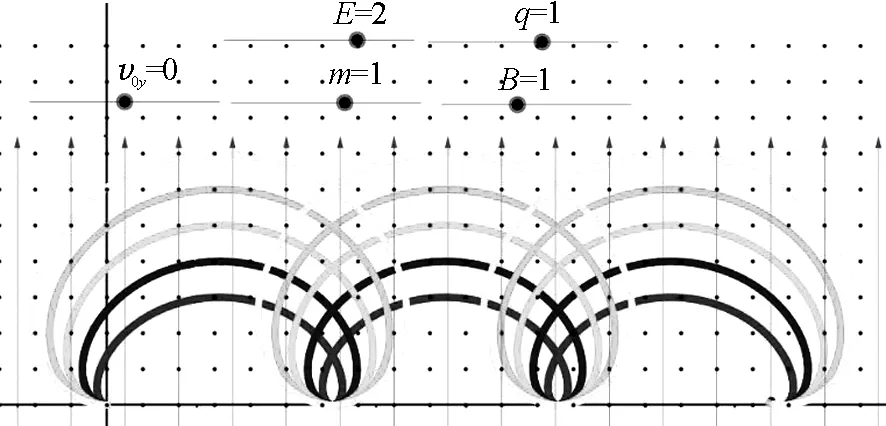
图6 粒子沿x轴负半轴射出的运动轨迹

情况二：粒子沿y轴方向以初速度为v0y射出,改变v0y的大小,观察粒子运动轨迹的变化.

(1)当粒子以一定初速度沿y轴正半轴射出,速度v0y的大小依次设为2、3、4、5、6等数值,其所对应的运动轨迹顺序依次为由里到外的长摆线,如图7所示.

图7 粒子沿y轴正半轴射出的运动轨迹

(2)当粒子以一定初速度沿y轴负半轴射出,速度v0y的大小依次设为2、3、4、5、6等数值,其所对应的运动轨迹顺序依次为由里到外的长摆线,如图8所示.

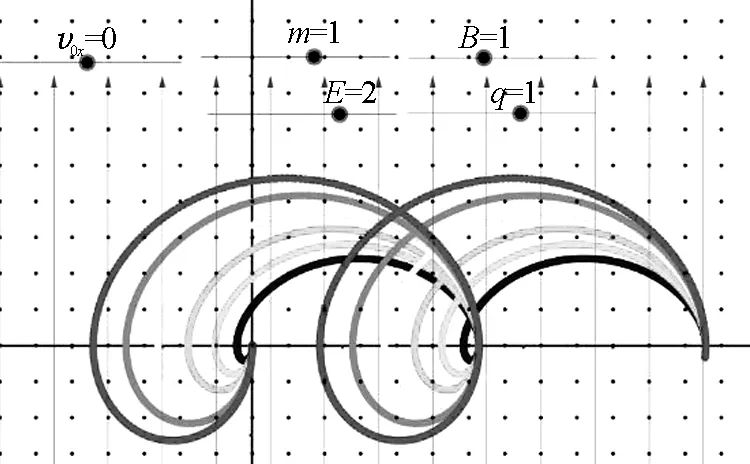
图8 粒子沿y轴负半轴射出的运动轨迹

由粒子在复合场中的运动方程,模拟出任意情况下带电粒子的运动轨迹.在教学中,让学生既具有物理观念、科学思维,也具有发现物理美的眼睛.正如庄子所言:判天地之美,析万物之理.“理”是物理学中的概念、定律、公式,是自然界遵从统一的物理规律方程;“美”是物理世界中的色彩、线条、图画,是自然界所呈现的和谐统一的图景.教师要善于引导学生用美的眼睛去欣赏物理学,揭示物理规律的统一美、物理公式的简洁美、物理图像的和谐美.

2.4 定性分析带电粒子在复合场中的运动

2.4.1 试题情境

【例2】(1988年高考全国卷物理试题)设空间存在向下的匀强电场和垂直纸面向里的匀强磁场,如图9所示.已知一离子在电场力和洛伦兹力的作用下,从静止开始自A点沿曲线ACB运动,到达B点时速度为零.C点是运动最低点.

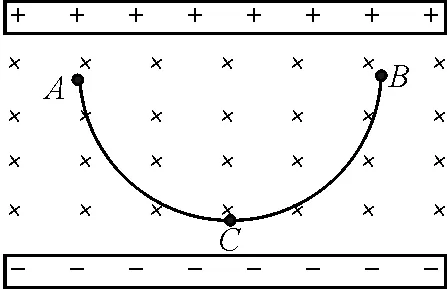
图9 例2题图

【例3】(2022年高考广东卷物理试题)如图10所示,磁控管内局部区域分布有水平向右的匀强电场和垂直纸面向里的匀强磁场.电子从M点由静止释放,沿图中所示轨迹经过N、P两点.

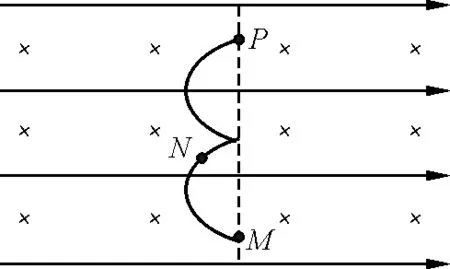
图10 例3题图

2.4.2 定性分析

(1)运动轨迹分析

在例2和例3两题中,只需要定性描述带电粒子在复合场中运动.依据两题所创设的物理情境,设计相应模拟动画.在原有设计程序基础上,调节滑动条,使动画中电场、磁场方向与问题情境保持一致,确定粒子电性以及速度,模拟带电粒子运动路径.在两题情境中,分别以A、M为运动起点,且由静止释放.例2和例3的运动轨迹分别如图11和图12所示,模拟轨迹与题图中的轨迹完全符合.从两题中可看出,粒子运动情境各有不同,但运动规律始终如一.从局部区域的运动到整体周期性运动,学生对粒子运动轨迹分析从静态局部分析走向动态全过程分析,对粒子运动认识会更深刻,提高理解能力.

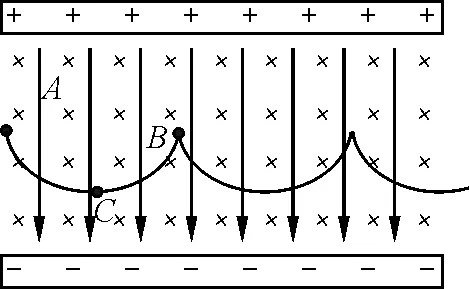
图11 模拟例2运动轨迹

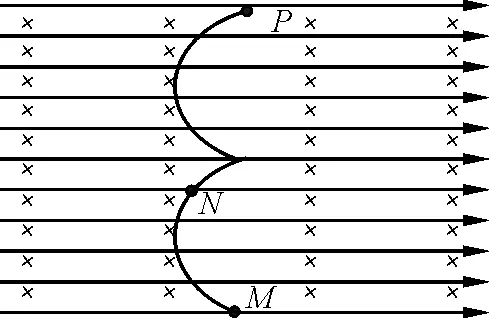
图12 模拟例3运动轨迹

(2)运动速度分析

基于已有设计,开启对合速度v的跟踪,可直观演示粒子运动时的速度变化.如图13和图14所示.用带箭头的线段表示粒子运动的速度,箭头的方向表示速度的方向,线段的长短表示速度的大小.可明显看出,例2中的离子从A点到C点速度逐渐增大,C点到B点速度不断减小,因此C点是速度最大的点;例3中的电子从M点运动到P点,速度随运动轨迹发生周期性变化,M点的速度与P点的速度相同且为零.学生从多角度、多维度定性分析粒子运动,既对粒子运动认识更全面,也增加了对抽象物理量变化过程的感性认识.定性分析是定量研究的基础,下面笔者将运用GeoGebra软件定量研究带电粒子的运动.

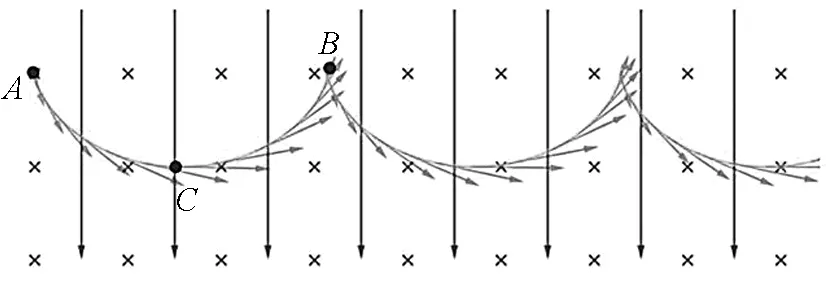
图13 例2中粒子速度变化

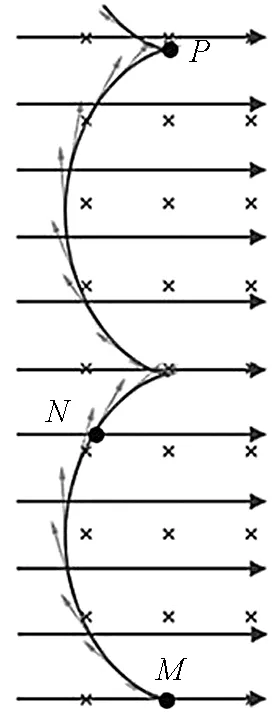
图14 例3中粒子速度变化

2.5 定量研究带电粒子在复合场中的运动

2.5.1 试题

【例4】(2013年高考福建卷)空间存在着范围足够大的匀强磁场和匀强电场,磁场的方向垂直于纸面(xOy平面)向外,磁感应强度为B,电场的方向沿y轴正方向,电场强度为E.一带正电粒子的质量为m,电荷量为q,不计重力.

(1)粒子在电场和磁场的作用下从坐标原点O点由静止开始运动,求释放后的粒子在运动过程中能达到的最大速度.

(2)粒子在电场和磁场的作用下从坐标原点O点以初速度vy沿y轴正向发射,求出发射后的粒子在运动过程中的最大速度.

2.5.2 配速法

配速法是指给带电粒子配上一对等大反向的速度,其中一个速度所产生的洛伦兹力与电场力相抵消,另一个速度产生的洛伦兹力使粒子做圆周运动.配速法的目的是产生抵消电场力的洛伦兹力,将“多力”问题转化为“多速度”问题,因分运动具有独立性,在求解速度问题上会更容易.

(1)粒子静止在坐标原点,给粒子配上一对等大反向的速度v1、v2,v1产生的洛伦兹力qv1B与电场力Eq相抵消,v2产生的洛伦兹力为qv2B,如图15所示.此时粒子运动是以速度v2绕O做匀速圆周运动,同时又以速度v1做匀速直线运动,粒子合速度v合为v1、v2的矢量合成速度,如图16所示[3].

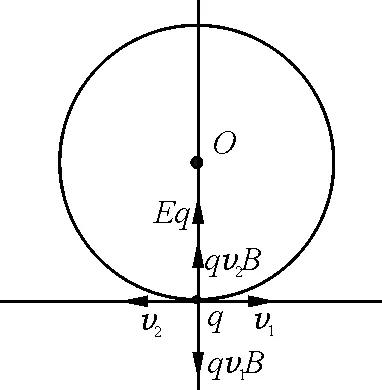
图15 例4(1)问配速法

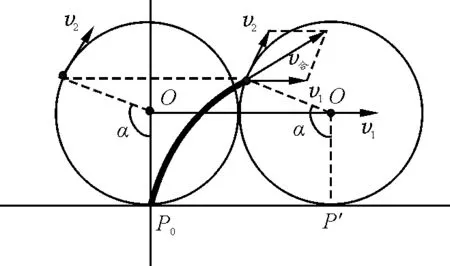
图16 例4(1)问运动合成分析

(2)粒子在坐标原点以速度vy沿y轴射出,同样地给粒子配上一对等大反向的速度v1、v2,v1产生的洛伦兹力qv1B与电场力Eq相抵消,此时v2与vy的合速度为v,v产生的洛伦兹力为qvB,如图17所示.因此,带电粒子以速度v绕O′做匀速圆周运动,同时又以速度v1做匀速直线运动,粒子的合速度v合为v、v1的矢量合成速度,如图18所示.

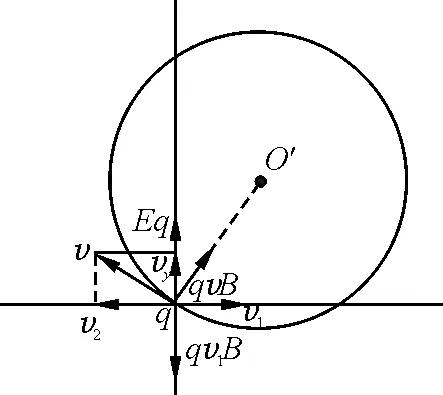
图17 例4(2)问配速法

图18 例4(2)问运动合成分析

2.5.3 定量研究

(1)通过GeoGebra课件演示带电粒子运动过程中合速度的方向、大小的改变,让学生感受运动一个周期的粒子速度的变化,看出粒子在x坐标轴上的速度为零,如图19所示.紧接着进行定量研究,如图20所示,由于v1与v2的大小不变且大小相等,当粒子达到摆线最高点时,合成速度达到最大值,此时v合=v1+v2,只需求出v1就能算出v合的最大值.先定性后定量,利于学生分析速度的变化,进一步推理出最大速度,提高分析推理能力.

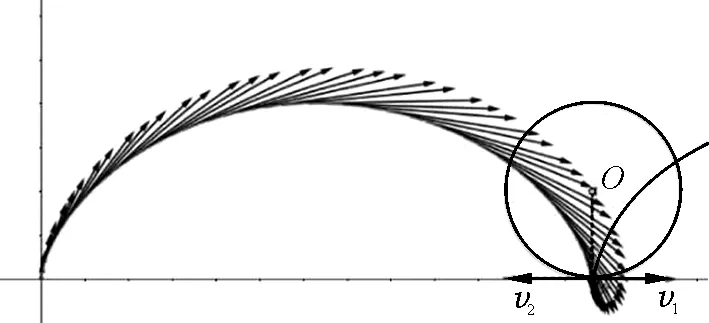
图19 感受合速度变化特点

图20 分析最大速度

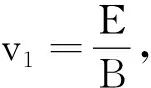
(2)同样地先通过动画演示,让学生感受粒子以初速度vy沿y轴正向发射后的速度变化特点,如图21所示.随后定量研究运动一个周期的粒子速度达到的最大值,分速度v的方向改变但大小保持不变,分速度v1的方向、大小均保持不变.当粒子运动到长摆线最高点时,分速度的矢量合达到最大值,vmax=v1+v,如图22所示.

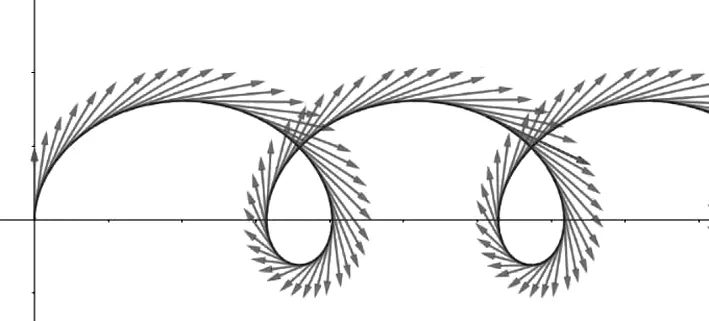
图21 感受合速度变化特点

图22 分析最大速度

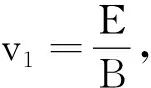
v2与vy合成的合速度

此时粒子的最大速度为

3 总结

通过应用GeoGebra软件研究带电粒子在复合场中的运动,发现该软件能将复杂的粒子运动过程可视化,对物理教学具有重要作用和价值.第一,对培养学生建模能力可谓是锦上添花,更有助于理解和分析抽象的物理过程;第二,拓宽学生思维,由一问变成多问,由一解变成多解,由一题变成多题,同时启发学生“多题归一”;第三,发挥物理学科育人功能,开展美育教育,感受物理美,欣赏物理美,创造物理美;第四,有利于试题改编与校对,确保学校出题的科学性和有效性,提高教师教学水平.一言以蔽之,GeoGebra软件让物理学可视化,也让物理学的美可视化.但当我们在享受计算机带给教学益处的同时,也不应忘记教学初心,计算机辅助教学却永远是辅助而不能成为“代替”.