基于牛顿环的拓展性实验方案设计*

李雪琴 唐艳妮 刘 芯 何楚洹 芦 静

(火箭军工程大学基础部 陕西 西安 710025)

牛顿环由牛顿在1675年首先在实验中观察到,是一种典型的薄膜等厚干涉现象,能充分表现出光的波动性.利用牛顿环干涉测量平凸透镜曲率半径是大学物理实验教学的基本内容,为了扩展学生思维,加深对光的等厚干涉原理的理解,提升知识的综合应用能力,本文基于牛顿环等厚干涉原理,从实验内容与实验方法方面进行拓展,设计了多种不同的拓展性实验方案,如图1所示,较大地丰富了牛顿环等厚干涉的实验内容,能够激发学生的实验探究热情.

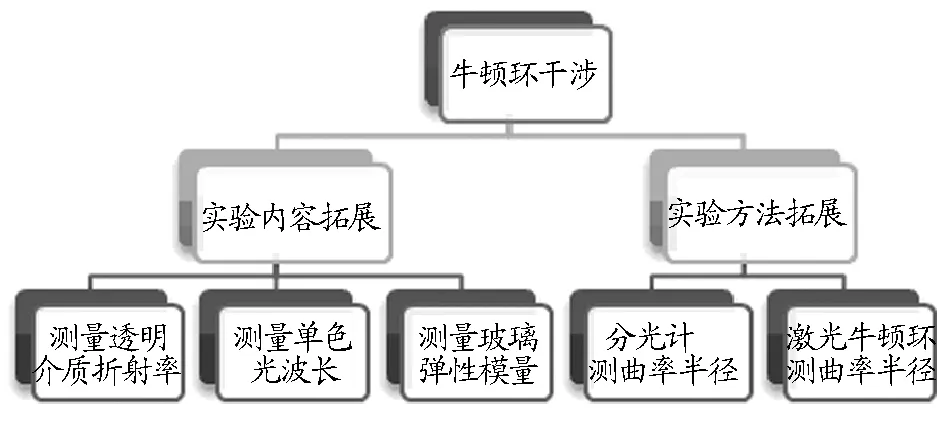
图1 基于牛顿环的拓展性实验方案设计

1 牛顿环干涉的基本原理

将一块曲率半径较大的平凸透镜的凸面放在一块平板玻璃上,这种结构即为牛顿环仪,如图2所示.在牛顿环仪的透镜凸面和平板玻璃间会形成一层空气薄膜,当平行的单色光垂直入射牛顿环仪,入射光将在这层空气薄膜的上下两表面依次反射,产生具有一定光程差的两束相干光.两束反射的相干光在相遇时的光程差取决于产生反射光的薄膜厚度,薄膜厚度相同处产生的两束相干光的光程差相等,将形成同一级干涉条纹,即为薄膜等厚干涉,其光路如图2所示.牛顿环仪中薄膜厚度从中心接触点到边缘逐渐增加,干涉图样是以接触点为中心的一系列明暗交替的同心圆环即牛顿环,且通常情况下干涉图样中央为暗斑,如图3所示.

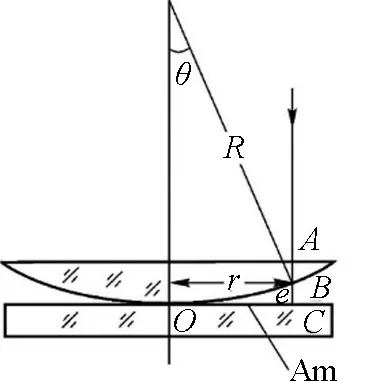
图2 牛顿环干涉光路

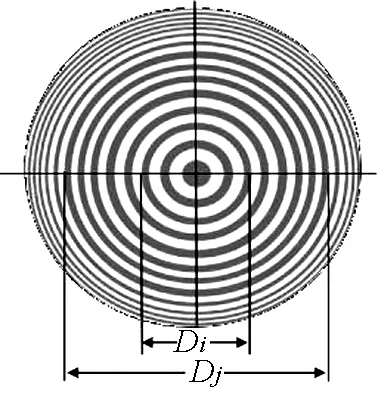
图3 牛顿环干涉图样

牛顿环不同级次暗纹直径Di、Dj与平凸透镜的曲率半径R、薄膜介质的折射率n、入射光波长λ满足下列关系

(1)

2 实验内容拓展

2.1 牛顿环干涉法测量介质折射率

根据式(1),在已知平凸透镜曲率半径的情况下,通过控制变量法可以测量透明薄膜介质折射率或入射单色光的波长.保持牛顿环曲率半径不变,入射单色光波长不变的情况下,改变牛顿环仪中填充的透明介质折射率,观察到的牛顿环同一级次的暗纹直径的大小将会发生改变.对同一牛顿环,采用同一钠光灯作为光源,对折射率分别n1、n2的透明介质薄膜,相同级次暗纹直径应满足下列关系式

(2)

因此可以通过测量不同介质薄膜产生的牛顿环暗纹直径,间接测量透明介质的折射率,例如测量不同质量浓度的氯化钠溶液的折射率.首先,在空气介质中调出清晰的牛顿环干涉图样,先用读数显微镜测量此时某级干涉条纹的直径Di1、Dj1;然后在牛顿环仪的两个玻璃片中间滴入不同质量浓度的氯化钠溶液,使平板玻璃与平凸透镜之间形成一层均匀的液体薄膜,再测液体薄膜干涉条纹的直径Di2、Dj2;最后通过牛顿环装置中空气膜和待测液体膜的干涉条纹直径与折射率的关系式(2),求出待测液体的折射率.

2.2 牛顿环干涉法测量单色光波长

在已知介质折射率的前提下,可以通过测量不同单色光牛顿环干涉图样相同级次的直径,间接测量入射光的波长.在牛顿环实验中,通常采用波长为589.3 nm 的钠黄光作为光源产生明暗相间的环形等厚干涉图样,其他不同波长的单色光照射在牛顿环装置上,也可以形成牛顿环干涉图样,但是同一级次的干涉圆环直径将会有所变化.对同一牛顿环,平凸透镜曲率半径和薄膜介质折射率不变,用波长分别为λ1、λ2的单色光照射同一牛顿环,根据式(1),相同级次暗纹直径应满足下列关系式

(3)

对同一个牛顿环仪,以波长为589.3 nm钠黄光为参考光源,分别测量钠光与待测单色光形成的牛顿环相同级次的直径,通过式(3)即可求得未知单色光的波长.高压汞灯发出的光线为复色光,可通过加装滤光片获取不同波长的单色光,形成等厚干涉牛顿环,如图4所示.通过测量牛顿环干涉图样不同级次的直径,可分别计算得到汞灯可见光范围内不同光谱线的波长.

(a) (b) (c)图4 汞灯不同波长光谱线牛顿环干涉现象

2.3 利用牛顿环实验测定玻璃的弹性模量

牛顿环干涉图样中央为一暗斑,表明暗斑区域空气薄膜厚度处处相等且为零,即此处平凸透镜和平板玻璃之间发生了形变(图5阴影部分).中心暗斑的大小由光学平板玻璃与平凸透镜接触端压力决定,接触压力越大,形变越大,牛顿环中央暗斑越大.

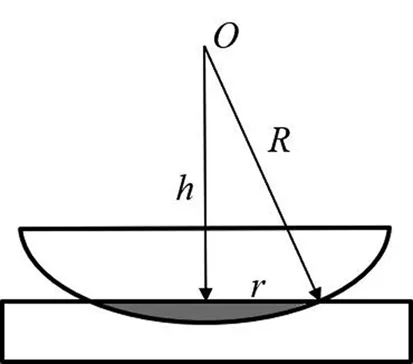
图5 牛顿环仪形变示意图

根据弹性力学理论,玻璃的弹性模量E与牛顿环中央暗斑半径r,满足下列关系[1]

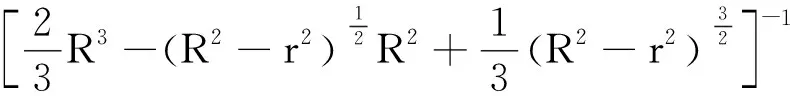
(4)

由式(4)可知,若测出施加的外力F、平凸透镜曲率半径R,以及平凸透镜体积V、平板玻璃体积V′,则可通过对接触面受到的压力及其产生的形变间接测量玻璃的弹性模量.

牛顿环仪在不同接触压力下的形变量用牛顿环干涉图样中央暗斑的面积来表征,接触压力越大,牛顿环干涉图样中央暗斑的面积越大[2].为了观察和测量牛顿环仪在不同压力下的形变量,我们采用3D打印的方式设计了一个牛顿环加压装置,实物结构如图6(a)所示,剖面结构如图6(b)所示.中央圆盘中间有一个圆形凹槽,内部放置平凸透镜与平板玻璃,构成牛顿环仪,中央圆盘下方由3根立柱支撑;最上方的圆形盖板通过3根连接柱连接下方的托盘,可在托盘加载不同质量的砝码,盖板中央有一个圆形孔洞,可用读数显微镜从正上方观察和测量牛顿环干涉图样.实验中通过加载不同质量的砝码改变牛顿环仪接触面压力,在不同压力下用读数显微镜分别测出中央暗斑左右切点位置,从而确定中央暗斑半径r.

(a)实物结构图 (b)剖面结构图图6 牛顿环加压装置

平凸透镜曲率半径的测定可在空气介质条件下,以波长λ= 589.3 nm的钠光源照射牛顿环仪,通过读数显微镜测量不同级次暗环直径,根据式(1)计算得到.平板玻璃的体积可分别利用游标卡尺及千分尺测出其直径与厚度计算得到.考虑到平凸透镜、平板玻璃材质相同,因此可用天平测量平凸透镜、平玻璃板的质量而间接测出平凸透镜的体积.将上述各个物理参量测量出来代入式(4)即可计算出玻璃的弹性模量.

3 实验方法拓展

3.1 分光计测量透镜曲率半径

由图2可知,牛顿环第k级暗纹半径rk及对应张角θk与平凸透镜曲率半径R满足下列关系

rk=Rsinθk

(5)

取空气介质折射率近似为1,即得

(6)

(7)

以上两式相减即得[3]

(8)

由式(8)可得,在已知入射光波长情况下,如果能够测量出各级暗纹的张角θ1、θ2,即可计算出平凸透镜的曲率半径R.

要用分光计观察和测量牛顿环,必须将分光计的望远镜改造成一个显微镜.实验中将望远镜物镜换成短焦距凸透镜(f=65 mm),使其与望远镜的物镜构成一个显微镜[4],用来观察牛顿环现象,改造后的实验装置如图7所示.

图7 分光计观察和测量牛顿环实验装置

钠光灯发出的光线经平行光管后出射平行光,经45°倾角的半透半反镜反射后垂直照射牛顿环,调节望远镜使其对准牛顿环仪中心,前后移动望远镜目镜进行调焦,使看到的牛顿环图样位于改装后的显微镜系统的视场中央位置,并且保证左右两侧看到的牛顿环级数尽可能相同且清晰.

一方面由于分光计望远镜改装后的等效显微镜系统只能绕着分光计中心转轴转动,不能平移,另一方面等效显微镜视场直径较小,只能清晰地观察到小角度范围内的牛顿环图样,所以实际测量时选择第5环至第10环暗纹对应的张角进行测量.将各级暗纹对应的张角代入式(8),可计算出透镜曲率半径.

3.2 激光牛顿环干涉法测量透镜曲率半径

传统的牛顿环仪由一个曲率半径很大的平凸透镜和一块光学平板玻璃构成,使用波长λ=589.3 nm的钠光光源测量透镜曲率半径,这种方法的主要缺陷是牛顿环仪两镜面的接触点由于压力产生变形,导致测量误差较大.由于氦氖激光的相干长度很大,远大于平凸透镜厚度对应的光程,因而可仅用一个平凸透镜镜片构成激光牛顿环仪进行测量,避免了传统牛顿环仪形变的影响,光路设计如图8所示.波长为632.8 nm的氦氖激光经扩束镜和准直镜后,出射光为平行面光源,经45°倾角的半透半反镜后,垂直照射到待测透镜,在待测透镜正上方即可用读数显微镜观察到激光牛顿环现象.

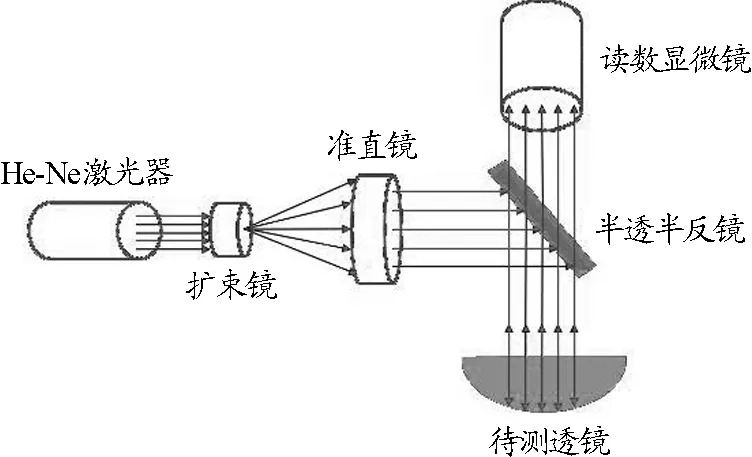
图8 激光牛顿环干涉光路示意图

由于氦氖激光的相干长度远大于平凸透镜的厚度,如图9所示,当氦氖激光光线1垂直入射到平凸透镜时,在平凸透镜上下表面分别发生反射,反射光线2、反射光线3满足相干条件,产生干涉现象,在透镜厚度相同的地方形成同一级次条纹,即可观察到激光牛顿环干涉圆环.

图9 平凸透镜氦氖激光干涉光路原理图

设平凸透镜片中心最大厚度为H,第k级暗环半径为rk,第k级暗环对应的透镜厚度为h,透镜折射率为n,令e=H-h,对第k级暗环

2nh=kλ

(9)

(10)

忽略高阶小量e2,则第k级暗环半径

(11)

第k+m级暗环半径

(12)

两式相减

(13)

将式(13)变为暗环直径平方差,可得曲率半径公式[5]

(14)

从上式可以得到氦氖激光的牛顿环与钠光牛顿环干涉现象明显的不同在于氦氖激光的牛顿环中心附近干涉级最大.

由于直接观察激光牛顿环会对人眼造成损伤,所以我们在显微镜的目镜端连接CCD,用显示器观察和测量激光牛顿环,如图10所示.利用读数显微镜测量不同级次激光牛顿环暗纹直径,代入式(14),可计算得到平凸透镜的曲率半径.

图10 CCD显示的激光牛顿环干涉图样

3 结论

在传统牛顿环实验的基础上根据牛顿环干涉图样的形态分布与影响因素,对牛顿环实验进行实验内容与实验方法方面的拓展.拓展实验方案融合了牛顿环等厚干涉原理、弹性力学理论、透镜组合成像及3D打印技术等,将波动光学原理、几何光学原理及光学仪器的调节和使用融为一体,知识综合性、应用性较强,在有效拓展学生思维能力的基础上,能够提高学以致用的实践创新能力.