基于逻辑学浅谈加速度概念教学*

张建军

(中山市第一中学 广东 中山 528400)

1 加速度概念教学困难的成因

加速度概念教学过程中,为使学生顺利地理解概念,常常要让学生观察体验,在此基础上加以引导,对感性材料进行比较、分析、综合,再抽象概括出加速度概念的本质.然而看似简单的概念,在实际教学中却出现诸多难点,其原因出在哪里呢?

1.1 概念同化带来的理解错误

概念同化是依靠新旧知识的联系,判别新学习的概念与原有认知结构中有关旧概念的异同,并组成概念的网络系统[1].概念同化的学习条件是学生认知结构中必须有同化新概念的有关旧概念,如若对旧概念没有准确理解,必然会对新概念的建立产生直接的影响.

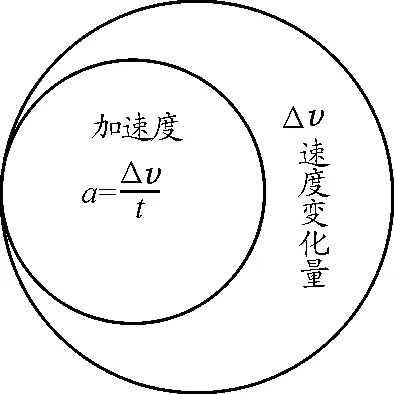
图1 速度变化量和加速度的关系

1.2 将属性概念错误地理解成实体概念

逻辑学中将概念划分为实体概念和属性概念,这是根据概念所反映的是对象本身,还是对象的属性不同划分的.实体概念是反映具体事物的概念,比如电场就是实体概念.属性概念是反映事物属性的概念,它反映的不是具体事物,而是事物的属性,比如电场强度就是属性概念[2].加速度比值定义式从逻辑学角度属于属性概念,在学生没有经历牛顿第二定律学习时,往往会对加速度的比值定义式产生误解,把比值定义式简单地理解为决定式,没有弄清比值定义的目的是为了反映运动特征,而不是反映本质属性.

学生学习加速度比值定义式和牛顿第二定律中间有一个时间跨度,教学时没办法将两者深入地结合起来去突破学生的理解困惑,这就给教学带来设计上的困难,也会对学生理解带来逻辑上的困惑.比如,加速度由Δv和Δt决定吗?加速度和Δv成正比和Δt成反比吗?速度方向发生变化加速度方向也跟着变化吗?速度为零加速度就一定为零吗?这些问题对于学生来说,是一个个不可回避的难题.许多教师为了化解这些问题选择回避,直接告诉学生加速度和速度、时间、速度变化量无关.此时学生对加速度的理解其实只停留在记得公式这个层面上,没有理解公式背后的含义.

2 基于逻辑学设计加速度概念教学

逻辑学中每个概念的形成都需要5个环节,即陈述、对比、抽象、概括、命名,教学结构如图2所示.

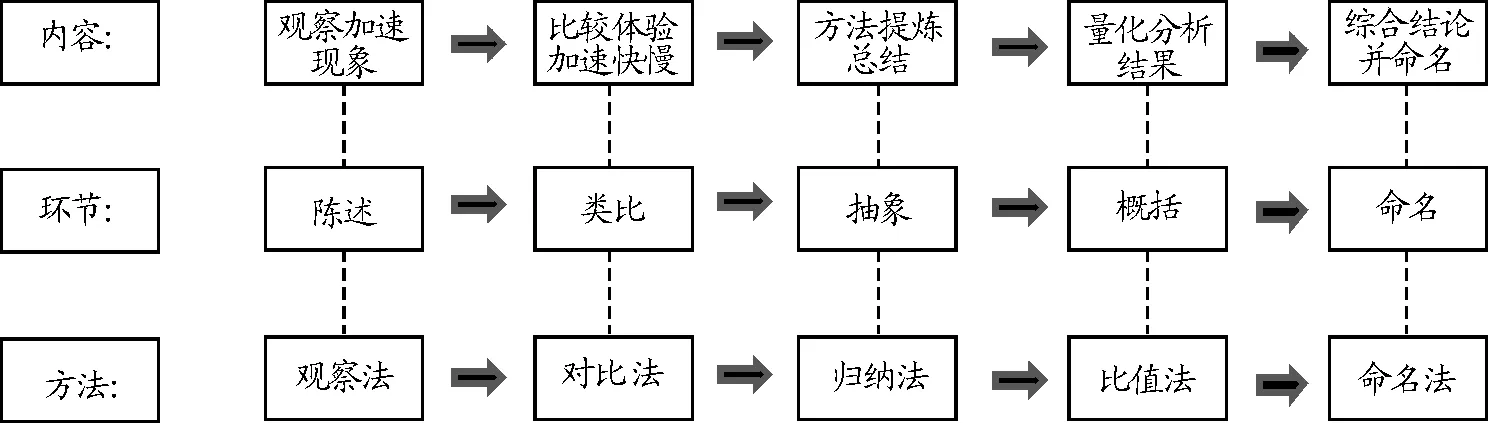
图2 逻辑学五环节教学结构

教师可以将教学内容、教学方法和5个环节融合,处理好5个环节的承接关系,协调好内容和方法上的逻辑关系,显化理论使教学更加高效流畅[3].加速度概念教学的对象是新升入高一的学生,逻辑思维还是经验型的,思维过程中具体形象仍然起主要作用,在实施抽象逻辑思维时,需要具象的经验支持,否则就会出现理解、判断、推理上的困难.然而抽象逻辑思维培养是高中教学的核心任务,这就需要教师在教学设计环节下功夫,将形象思维逻辑和抽象思维逻辑有机地结合起来,构建完备的教学流程,细化内容,优化方法,厘清五环节教学逻辑,让学生学得明白,悟得透彻.

2.1 形象逻辑支撑下的加减速体验

按照上述五环节教学流程,创设情境,设计有层次的系列问题,有序地开展教学.在陈述阶段基于学生体验,引入生活实例帮助学生建立加减速的实感情景.

以公园三人自行车(图3)为例,3人可以同时踩脚踏提供动力,也可以协同提供刹车阻力,辅助视频播放并提出问题.

图3 三人自行车

问题1:观察1人踩,2人踩,3人踩,哪种情景下加速较快?1人刹车,2人刹车,3人刹车哪种情景下减速较快?你是如何比较的,说出理由.

三人自行车情境中,学生基于生活体验,回答多集中在两点:“单位时间内速度增加得多,加速快,减少得多,减速快”“质量不变时,3人踩动力较大,加速快,3人刹车时阻力大,减速快”.这样的回答都在情理之中,是源于生活实践,基于体验的直接生成.这两个回答,不仅为加速度定义式的引入做好了铺垫,也为区别定义式和决定式做好了铺垫.让学生对加减速快慢的比较有了初步的思路和方法.

2.2 类比推理支撑下速度变化量的引入

通过定性的描述自行车加速和刹车现象后,引入表1的定量数据,引导学生继续分析.

表1 三人自行车速度变化量的描述

问题2:观察表1,想想如何描述速度的变化量呢?

根据多年的教学实践,学生的回答趋于一致:“用大的速度减去小的速度.”这个回答是基于生活经验的概括,例如:“身高从150 cm长到160 cm,身高变化是10 cm”“体重从60 kg减少到50 kg,体重变化了10 kg”,那速度变化量自然就是大的速度减去小的速度.此时教师不要立刻去纠正学生的错误理解,先让学生按照自己的理解把表1中Δv一栏填写完成,按照学生填写的结果提出问题.

问题3:1人踩踏板加速时取Δt=20 s,得Δv=10 m/s,1人刹车减速时取Δt=5 s,得Δv=10 m/s,两者速度变化量相同吗?

问题3的提出让学生在思维上产生冲突,一个加速一个减速肯定是不同的,此时教师再引导学生重新思考,总结出速度变化量的正确表达即Δv=vt-v0,其中v0、vt分别表示初速度和末速度,而不是用大的速度减去小的速度.按照正确的理解再让学生把修正后的结果填写到表1的最后一栏,再提出新问题.

问题4:能否用速度变化量描述物体加减速的快慢?

学生结合表1的数据不难发现,在1人踩踏板加速时,取Δt=20 s,3人踩踏板加速时,取Δt=5 s,有相同的速度表变化量Δv=10 m/s,但是两者的加速快慢显然不一样.对比分析后引导学生得出结论:“不能用Δv去描述加速的快慢,减速也是如此.”

2.3 抽象逻辑支撑下的速度变化量方向的深究

速度变化量Δv的方向是一个比较抽象的知识,学生在生活中没有具体的实践支撑,但是对它的理解直接关系到加速度概念教学的效果达成.此时,教师可以继续利用表1提出问题,和学生一起探讨.

问题5:表1中速度变化量的正负代表什么含义?

为了回答这个问题,首先对速度变化量做一个具象描述,帮助学生建立直观体验.选择一维运动进行研究,类比于位移的表示方法,取一带箭头的线段来表示速度,箭头方向为速度方向,线段长短表示其大小.取v0方向为正方向,若质点做加速运动则vt的线段长于v0的线段,根据Δv=vt-v0,可得Δv>0,方向和正方向一致,如图4所示;若质点做减速运动则vt的线段短于v0的线段,根据Δv=vt-v0,可得Δv<0,方向和速度方向相反,如图5所示.这种处理办法能够具象地反映Δv的方向性,从逻辑上也符合学生的认知规律.需要强调的是,正方向选择具有任意性,选择v0为正方向是基于方便.选择vt方向为正方向也可以,正方向的选择并不会改变Δv的方向.综合分析让学生归纳出结论:“Δv的正负表示方向,选取v0为正方向,若Δv>0表示物体做加速运动,若Δv<0表示物体做减速运动”.如果脱离v0方向为正方向,就不能简单地通过Δv>0或者Δv<0来判断加减速运动.

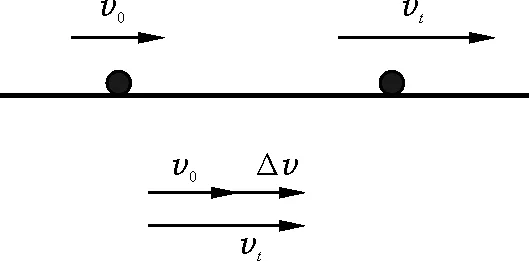
图4 加速时速度变化量矢量图

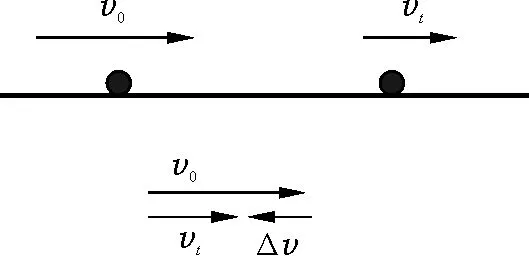
图5 减速时速度变化量矢量图

2.4 归纳概括支撑下加速度比值定义式的教学

比值定义法定义物理量时,依据其意义的不同,可分为两种类型:一类是两个物理量的比值是个定值,是物体固有属性的反映;另一类是描述物体外在的状态,不反映其固有性质,反映的是一种变化效果,属于状态反映[4].加速度的比值定义属于第二种类型的定义方式,反映的是速度变化快慢.

高一的学生没有深入研究过比值定义法,往往将加速度的比值定义式简单地理解为决定式,不知道加速度的本质和比值定义式之间的关系,以至于在实际运用中常常出现理解错误,甚至只是死记硬背、胡乱套用公式.为了解决这些理解上的困惑,教师需在教学过程中,仔细地梳理学生产生错误理解的逻辑障碍,运用科学的教学方法,引导学生突破思维障碍,达到理想的学习效果.这里依然选择三人自行车作为具体实例设计表2,并提出问题和学生一起探究.

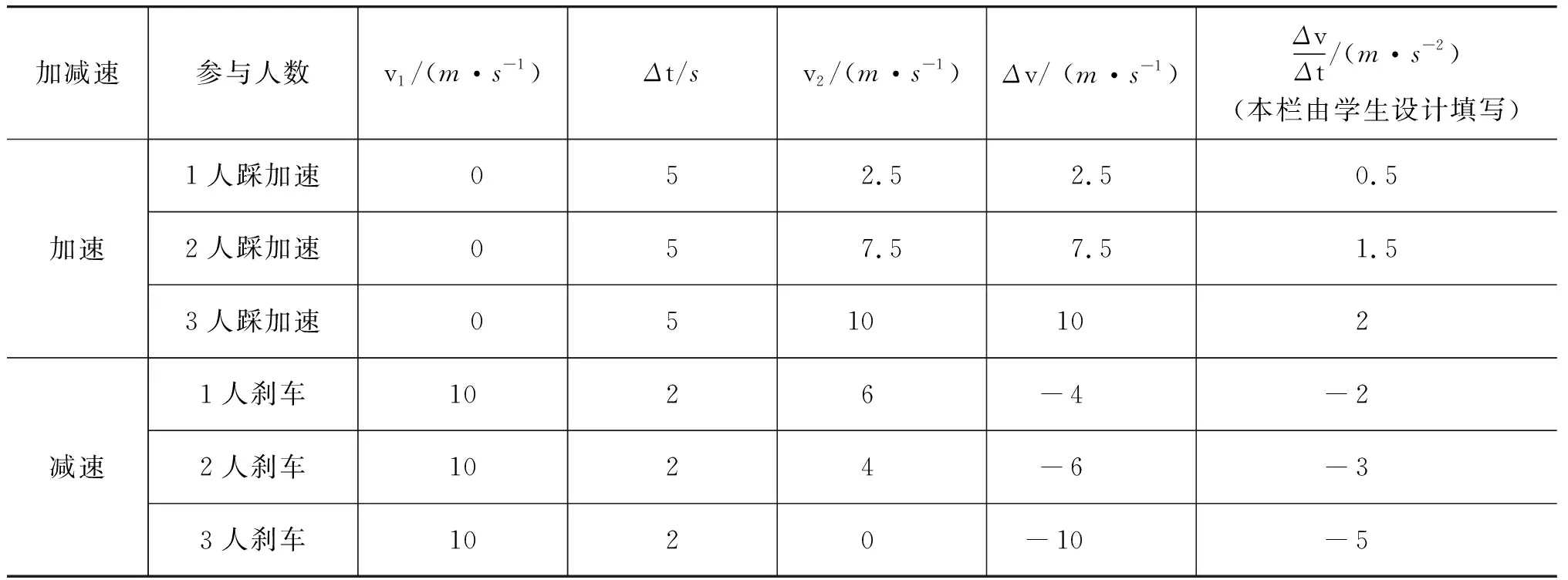
表2 三人自行车速度变化率

问题6:我们用什么量来描述三人自行车运动过程中加速和减速的快慢呢?请结合表2,提出你的想法,设计最后一栏,并加以归纳总结.

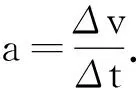
问题7:3人踩加速的加速度为2 m/s2,3人刹车时加速度为-5 m/s2,哪一个加速度更大呢?正负号有什么意义吗?

问题7起到了承上启下的作用,让学生将加速度的方向和速度变化量的方向联系在一起,即加速度的正负源于速度变化量的正负.既然速度变化量的正负表示方向,那么加速度的正负自然也表示方向,从而概括得出结论:“加速度正负表示方向,若选择v0方向为正方向,a>0表示物体做加速运动,a<0表示物体做减速运动,但不能脱离v0为正方向的前提.”

问题8:请大家回顾问题1,物体加速的快慢是由什么因素决定的呢?是Δv和Δt决定的吗?请大家结合表3,说说你的思考.

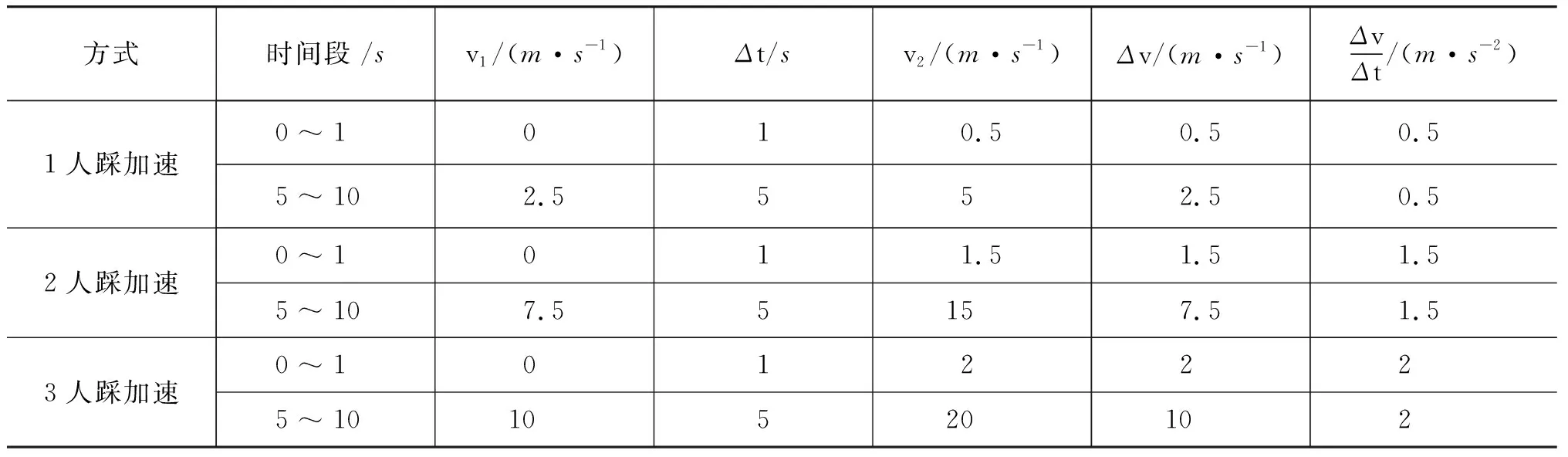
表3 三人自行车加速快慢对比

问题9:三人自行车行驶过程中,开始时由1人提供驱动力,接着由2人提供驱动力,最后由3人提供驱动力,这样的运动特点是什么样的?

问题9的提出目的是让学生深化加速度的理解,体会变加速度运动,这种运动很抽象,需要具体的实践帮助学生体验,这个实践又不能脱离运动本身.三人自行车就是一个很好的例子,学生经过前面的学习很容易就能概括总结出这个运动的特点,即做加速度逐渐增大的加速运动.同样的三人自行车,还可以先由3人提供动力,然后由2人提供动力,再由1人提供动力,对应着加速度逐渐减小的加速运动.刹车减速时,由1人制动到2人制动,再到3人制动,对应着加速度逐渐增大的减速运动;由3人制动到2人制动,再到1人制动,对应着加速度逐渐减小的减速运动.

2.5 辩证逻辑支撑下的加速度命名

经过前面的学习,学生对加速度有了比较深刻的理解,然而加速度的命名,有它的历史渊源.加速度英文名称是“acceleration”,来自拉丁语ad+celer,即“加+速”[5],英文含义有加快、加速、加速能力、加速的幅度等.国内直接被翻译为“加速度”,很容易让人错误地理解为增加的速度,这里把加速度理解为“速变率”或者“速变度”更为贴切,即速度变化的快慢程度.既然加速度和速度无关,是由力和质量决定,为何还要用从“速度”角度去命名呢,从辩证的角度去思考,人类认识自然过程中最初形成的概念是浅层次的初级概念,总是先反映对象的非本质属性,进一步形成的深层次概念才反映本质属性,加速度亦是如此,它呈现出来的首先是外部表现,是速度变化的快慢,而不是本质特征,因此从“速度”这个角度去命名更符合人类认识自然的规律.

3 结论

加速度是联系运动和力的重要桥梁,是非常抽象的概念,经历加速度概念的学习,不仅在物理思想上、物理方法上有重要意义,在培养学生的思维能力方面也有很大的作用.然而在学生的日常生活中,与加速度相关的体验并不多,这就给学生理解带来一定的困难,也给教学带来了很多困难,甚至一度被誉为最难构建的概念.

本文从逻辑学角度分析了加速度概念教学中常见的困难,并提供一种基于逻辑学的教学设计,比较科学地解决了这些困难.

4 结束语

加速度概念是中学物理教学的难点之一,因其涉及大小的计算和方向的确定,以及它与速度的关联性,对于中学生来讲是在学习时确实存在一定的难度.然而作为物理教师,如何正确有效地设计教学方案,如何引导学生深入思考,化解和降低加速度概念的理解难度,是有待我们继续研究的问题.