空间碎片多源数据融合定轨软件SPODFMD简介∗

杜建丽 徐 劲 杨 冬 曹志斌 马剑波

（1 中国科学院紫金山天文台 南京 210023）

（2 中国科学院空间目标与碎片观测重点实验室 南京 210023）

1 引言

空间碎片的轨道信息是空间态势感知的重点关注要素, 由其形成的编目数据库是太空资源开发利用、太空资产碰撞预警、太空垃圾清理等应用的基础, 其重要性得到了广泛的认可. 近20 yr来, 全球空间碎片专用、兼用和可用监测设备的数量大幅增长, 形成以美国空间监视网为代表的多个监测网, 设备类型主要为无线电雷达、光学望远镜和激光雷达, 同一目标被多个设备探测或跟踪的概率大大增加. 利用多站点、多类型设备获取的资料编目定轨是组网观测要解决的问题之一, 由于多站点组网改善了测量几何、增加了观测频率、可联合高精度资料, 融合定轨的精度优于单站定轨.

编目工作中的轨道计算有别于一般应用中的轨道计算, 不仅要求轨道计算的精度足以实现对空间碎片运动态势的精确掌控, 还要求有较高的轨道计算效率. 编目工作对轨道计算效率的最低要求是轨道计算的处理时间不能大于自动运行设备的数据采集时间, 以避免产生数据挤压的瓶颈效应, 使编目过程难以持续. 以编目目标2万、每天进行一次轨道更新计算为例, 单个目标的平均处理时间要求不大于4.32 s, 对编目定轨的计算效率要求很高. 当前编目工作中的轨道计算广泛采用分析方法, 例如美国采用SGP4 （Simplified General Perturbation）/SDP4 （Simplified Deep space Perturbation）分析模型, 国内编目工作通常采用拟平均根数法等. 虽然分析方法较好地解决了编目工作的时效性问题, 但随着观测技术的发展, 它的模型精度并不能与当前的观测精度（雷达测距精度优于20 m,光学测角精度优于10′′）相匹配, 从而不能达到理想的定轨精度, 制约了相关应用水平的提升, 因此数值方法在编目工作中具有潜在的应用价值. 另一方面, 现代计算机运算速度的不断提升也使数值方法应用于编目处理成为了可能. 数值法应用于编目定轨, 应转变应用于人造卫星定轨时“一星一方案”的处理思路, 重点解决通用性、时效性差的问题, 具体的研究方向为扩展数据类型、提升计算速度、全轨道类型适用以及海量数据带来的计算稳健性要求等.

作者在以下方面做了大量有益探索, 包括调研国内主流空间监测设备情况（设备类型、安装方式、资料类型等）,调研空间碎片数据处理现状和改造要求（精度和速度等）, 针对数值法轨道改进计算耗时的关键环节研发兼顾精度和效率的优化算法,针对极性奇点和数学奇点进行无奇点化处理, 针对多源数据先验精度失真进行自适应加权方法研究等, 以上调研结果和研究结果是形成SPODFMD（Space debris Precise Orbit Determination Fusing Multi-source Data）软件架构和定轨算法的基础.本文将首先介绍软件的功能和特点, 再介绍软件集成的关键技术, 最后利用多源数据进行测试并根据测试结果总结软件的性能.

2 软件的功能和特点

SPODFMD软件能满足绝大部分主流空间监测设备获取数据的融合需求, 并且具备多种特点.

2.1 软件功能（见附录）

2.2 软件特点

多资料:软件支持14类设备的数据输入和任意融合, 设备类型见附录.

高效性:软件的效率在定轨算法和编程技巧两方面得到了优化. 算法方面, 一方面采用了先积分再插值的策略替代逐点积分, 一个轨道周期积分的基点数随偏心率增大由25递增至最多80个, 实际构造的基点数只需要覆盖星历点即可, 由于插值效率很高,星历的计算时间约等于插值基点的积分时间,相比逐点积分密集星历节省了大量时间;另一方面,计算一次积分最为复杂的项是地球重力及其偏导数的计算, 其耗时程度随阶数的增加呈平方增长,M´etris系数变换法可以解决这一问题, 无论是计算重力势还是重力势的任意阶偏导数, 都可转换为球谐级数的求和, 球谐项的系数可事先通过变换一次求出, 再次节省了计算时间. 此外, 在计算大气密度相对于地固矩坐标的偏导数时采用了解析表达式,相比有限差分求导需要多次计算大气密度的效率要高. 编程技巧方面, 软件采用了高效的排序方法、搜索算法、滑动窗口法等进一步提高计算效率.

通用性:软件适用于低、中、高轨各种偏心率的全轨道空间碎片. 偏心率通用性主要通过非均匀插值基点构造方法和多种积分器来实现, 非均匀插值基点构造方法是针对大偏心率轨道利用均匀基点插值时近地点和远地点星历精度失衡这一状况提出的, 实际上适用于任何偏心率轨道, 可与任一单步法积分器结合使用; 软件提供了4种积分器以及3种组合积分器以适应轨道偏心率的变化, 其中AC （Adams-Cowell）积分器适用于偏心率小于0.1的轨道, 而RKF （Runge-Kutta-Fehlberg）、RKNF（Runge-Kutta-Nystrom-Fehlberg）和Everhart适用于任何偏心率轨道. 轨道高度的通用性主要通过定轨流程实现, 除6个轨道根数外, 高轨目标同时改进与光压相关的物理量,低轨目标同时改进与大气相关的物理量, 中轨目标同时改进与大气和光压相关的两个物理量, 通过对空间碎片轨道高度的区分实现了轨道高度全覆盖.

稳健性:软件的稳健性主要体现在无奇点上.软件集成了两种地球重力势及其偏导数算法, 分别为Balmino和M´etris系数变换法, 它们的共同特点是都进行了无奇点变换, 计算两极上空空间点的引力和偏导数均不会引起定义和计算的奇点.DTM94 （Drag Temperature Model）大气密度模型也具备无奇点变换的条件, 经过与地球重力势相同的处理后也达到了消除奇点的效果, 进一步提升了软件的稳健性.

模块化:软件采用模块化设计, 将功能独立且有重复使用需求的函数全部采用模块管理, 由此带来了程序设计的灵活性, 例如动力学模型共有24个相关模块, 分别用于定轨/预报、低/中/高轨、Balmino/M´etris、1/2阶积分器及以上4类配置选项的任意组合, 例如“定轨+低轨+M´etris+2阶积分器”对应一个单独的模块, 程序的修改、调用非常便利, 也便于实现更为复杂的功能.

灵活性:软件的灵活性是指多资料这一特点在概念上的延伸, 软件支持的14类设备是逻辑设备的概念, 逻辑设备可与实际设备一一对应, 也可与实际设备完全不同, 应根据数据特点和融合需求灵活设置设备的类型. 例如一台相控阵雷达, 由于测距精度远高于测角精度, 若仅使用测距资料与其他高精度测角设备获取的数据融合, 调用软件时仅需要将相控阵雷达的设备类型设置为激光雷达. 类似的场景还有将一台激光测距和测角设备作为单基雷达三元素设备进行输入等, 采用逻辑设备的理念使得数据融合场景更加丰富、人性化.

智能化:智能化体现在软件对物理参数改进方面的处理, 除6个轨道根数外, 定轨时还尝试同时改进与目标相关的物理参数, 如果迭代发散或改进值不合理则自动固定其物理参数重新改进, 整个过程无需人工干预.

信息全反馈: 软件处理的所有环节都会反馈必要的信息, 通过17类反馈信息的值可追溯不合理的输入、积分异常、堆栈异常等问题, 符合工程应用对软件的要求.

3 关键技术

SPODFMD软件集成的关键技术主要有地球重力势及其偏导数无奇点快速计算方法、无奇点DTM94大气密度模型及其偏导数的解析表达方法、大偏心率轨道密集星历精密快速计算方法以及稳健的自适应加权方法等. 这些算法虽然是为解决某一问题而提出, 但在开发过程中都兼顾了定轨对效率、精度、通用和稳健的要求, 它们的集成就是从各个角度同时对定轨过程进行优化, 最终决定了SPODFMD软件的效果.

3.1 大偏心率轨道密集星历精密快速计算方法

编目工作的轨道计算普遍涉及密集星历的产生和计算问题, 星历点密集时逐点积分步长不能得到充分伸展, 积分右函数计算次数大大增加, 严重降低数值方法的计算效率, 避免这一问题的有效技术手段就是运用内插方法. 目前产生密集星历的多种内插方法均采用了定步长划分插值基点的方式,这种方式适用于运动特征变化非常平缓的近圆轨道, 对于编目工作中经常涉及的运动特征变化较为剧烈的大偏心率轨道并不适用, 易造成近地点附近星历因插值基点稀疏导致插值精度低, 而远地点附近星历又因插值基点密集而精度过高的失衡状况.可通过增加插值基点的数量来改善这一失衡状况,但相应需增加数值积分时间,这又易降低计算效率.为兼顾大偏心率轨道整体的星历计算精度和计算效率, 提出一种非均匀插值基点构造方法[1–3], 具体为从已知星历的初始基点开始递次构造插值基点,待构造的基点由上一个基点的星历计算得出, 基点的星历由数值积分得出, 基点构造与数值积分计算交替进行,直到将涵盖所有插值点的基点构造完毕.非均匀插值基点的构造方法见（1）式,基点间隔是空间目标地心距的函数, 该方法可以与一般的单步积分法在星历计算过程中协调使用, 当与Hermite插值多项式结合使用时总效率最高.

其中, ∆Tl为第l个插值基点与待构造的第l+1个基点的间隔;a为轨道半长径; γ为时间变换参数; β为轨道周期变换因子;Rl为利用第l个基点星历计算得出的地心距;Pt为以时间变量t计算的轨道运动周期;N为一个轨道周期内插值基点的数量. 此外,γ和N为插值基点构造之前预先确定的常量, γ由数值实验结果确定的最佳普适数值为0.3, β由轨道偏心率e和γ的取值决定, 在基点构造过程中也是一个常量.

3.2 地球重力势及其偏导数无奇点快速计算方法

地球重力势通常表达为球坐标的函数, 这种表达方式引入了计算奇点, 表现为两点: （1）位于两极上空点位的经度定义不明确; （2）求解重力势相对于地固矩坐标偏导数时分母出现纬度余弦,在两极上空时引起分母为零. 从物理角度考虑,地球外部重力势连续分布不存在局部奇点, 上述奇点非本性奇点而是数学奇点, 通过引入适当的数学方法可以消除. Pines[4]首先引入了地球重力势的一种无奇点表达形式, 将由勒让德多项式表达的地球重力势球谐函数转换为由亥姆霍兹多项式表达, 并引入地心距和方向余弦取代球坐标;Balmino等[5]对Pines[4]的结果作了进一步的整理和完善, 他们的基本思想都是利用复合求导法则将重力势相对于地固坐标的一、二阶偏导数转化为相对于地心距和方向余弦的偏导数, 经转化后的偏导数不会在分母上产生纬度余弦的因子, 因此是无奇点的. Hotine[6]发现任何球谐级数相对于矩坐标的偏导数还可以表示为一个球谐级数, 于是将地球重力势相对于地固矩坐标的偏导数计算转变为一种系数变换, Bettadpur[7]做了进一步的研究和改进. M´etris等[8]吸收了Bettadpur[7]和Pines[4]方法的结论, 对重力势展开式中所有单个立体球谐项的Cunningham[9]结果进行求和, 并对和式中的立体谐函数按度和阶进行归并和整理, 得到了重力势相对于地固矩坐标偏导数的无奇点紧致公式, 偏导公式在形式上完全类似于原重力势表达式, 其谐系数和部分变量与原系数和原变量之间存在变换关系, 需要变换的量为:µ →µ′,N1→N′1,N2→N′2,以及L →L′的变换,上述变量的具体定义及变换方法见下文（2）–（3）式.

SPODFMD集成了Balmino和M´etris两种计算方法. 软件集成的Balmino方法对原公式中分开处理的地球中心引力项、带谐项和田谐项作了统一处理, 表达简洁且便于计算机程式设计, 其不足之处在于需要递推计算亥姆霍兹多项式及其一、二阶偏导数, 影响计算效率. M´etris方法实际为Hotine算法的一种推广, 是迄今为止能够实现地球重力势二阶以上高阶偏导数的唯一方法, 无论是计算重力势还是重力势的任意阶偏导数, 其计算形式是统一的, 均为球谐级数的求和, 只是球谐项的系数不同. 鉴于这些系数可事先通过对应的变换求得, 大大节省了计算时间, 当不考虑地球重力势谐系数的变化时（如忽略潮汐的影响）, 至少可节省30%的计算时间[10].

设U为重力势或其对地固矩坐标的任意阶偏导数, 且有形式:

原形式中,µ为地心引力常数;n和m分别为球谐级数展开式所截取的阶和度,N1和N2分别为n的下限和上限;L为z坐标偏导的阶次, 原形式中其值为零;Cnm和Snm为归一化的球谐系数,Hnm为归一化的赫姆霍兹多项式, 且有γm= cosm ϕcosmλ,σm= cosm ϕsinmλ,λ和ϕ分别为目标点的经度和纬度. 则U相对于矩坐标（x,y,z）求任意阶（i,j,k）的偏导数公式为:

3.3 自适应加权方法

具有不同测量精度的多类型资料融合时需重点考虑权的分配问题, 常见的做法是根据资料的先验精度加权, 先验精度失真易造成轨道改进质量的下降. 考虑到精度失真是一种常见现象, 提出了一种稳健的自适应加权方法, 自适应权是在固定权轨道改进收敛的基础上利用资料残差重新分配权重直至收敛的过程, 其特点在于: （1）自适应加权定轨利用了固定权轨道改进收敛的结果作为初根数, 因此启动前会默认先执行固定权定轨, 这样处理可避免直接使用自适应权时（自适应权由初轨预报值与资料值的残差确定）过度依赖初根数的精度, 这种依赖性使得轨道改进偏离真值的概率大大增加, 甚至出现发散现象;（2）自适应权定轨过程中不再剔除观测资料, 利用固定权轨道改进最后一次迭代剔除野值后的全部资料参与自适应定轨, 这样处理既对精度失真资料的权进行了一定程度的纠偏, 又保证了自适应迭代的稳健性, 通常自适应权定轨仅需要少量的迭代即可收敛, 不会显著增加计算时间.

3.4 无奇点DTM94大气密度模型及其偏导数的解析表达方法

在低轨目标编目定轨中需要考虑大气阻力摄动, 对于轨道特别低或者面质比特别大的低轨目标, 大气阻力摄动已与地球主要带谐项J2项摄动相当, 因此为了保证定轨迭代过程的收敛, 还必须计算大气阻力相对于目标位置和速度矢量的偏导数. SPODFMD采用了DTM94热大气模型[11], 其为三维模型具有精度高的优点, 但由于也采用球坐标作为基本变量, 因此模型本身及其相对于地固矩坐标的偏导数也存在极性奇点; 另一方面, 目前除Harris-Priester大气模型已有成熟的偏导数解析表达式外, 其他大气模型均因过于复杂难以求导,利用差分计算偏导数是常用的替代方法, 然而当模型不连续或不可微时, 差分计算结果失真.

鉴于DTM94原模型中存在勒让德多项式, 同样借鉴Pines[4]消除地球重力势球谐表达式奇点所用的方法, 用目标地心距以及方向余弦取代球坐标作为DTM94大气模型的基本变量, 变换后的大气密度模型是无奇点的, 且使得寻求大气密度相对于空间目标地固矩坐标的解析表达成为可能.借鉴Pines[4]提出的复合求导法则, 提出了大气密度ρ相对于地固矩坐标的表达公式[12]:

其中,j= 1,2,3,ρ=ρ（x,y,z）为x、y、z的连续可微函数, 且有X1=x,X2=y,X3=z,r、θ1、θ2、θ3分别为目标的地心距和地固坐标系下X、Y、Z轴上的方向余弦.相比差分求取偏导数的方法,解析表达式具有准确、稳健和高效的优势.

4 测试与分析

多源观测数据有两层含义, 一是指来源于多个测站, 二是指多种数据类型, 两者满足其一即可称为融合定轨, 以下将通过算例来测试软件的性能,主要关注指标为定轨精度和定轨时间.

4.1 单站资料定轨

单站资料指一台“逻辑设备”同时获取的测轨资料,例如雷达可同时获取测角和测距三元素资料,有的雷达还能获取包括测速在内的四元素资料. 同时获取的三元素或者四元素都是单站资料, 大部分单站资料都是由单台实际设备获取的, 也有部分单站资料涉及到收发分置的两台实际设备, 例如双基雷达的距离和资料以及无线电时差和频差资料, 此时一台“逻辑设备”由两台实际设备构成. 包含同类型数据的单站资料, 例如激光测距、光电测角这类资料由于仅包含一种元素或者精度相同的两种元素, 定轨时等权分配权重即可, 而三元素和四元素资料包含了不同精度的测角、测距和测速3类数据,即便来源于同一设备, 也涉及不同数据类型的融合问题, 空间碎片多源观测数据融合定轨软件采用马尔可夫估计理论, 利用数据的先验精度确定各元素的权重, 解算结果稳定准确. 以下通过例子来说明单站资料的定轨能力, 各算例的数据类型、时间跨度和数据量等关键信息列于表1, 利用这些资料的定轨性能主要指标列于表2, 采用的主要动力学模型和公共配置参数见表3.

表1 单设备（SE）获取的数据资料Table 1 Data from Single Equipment （SE）

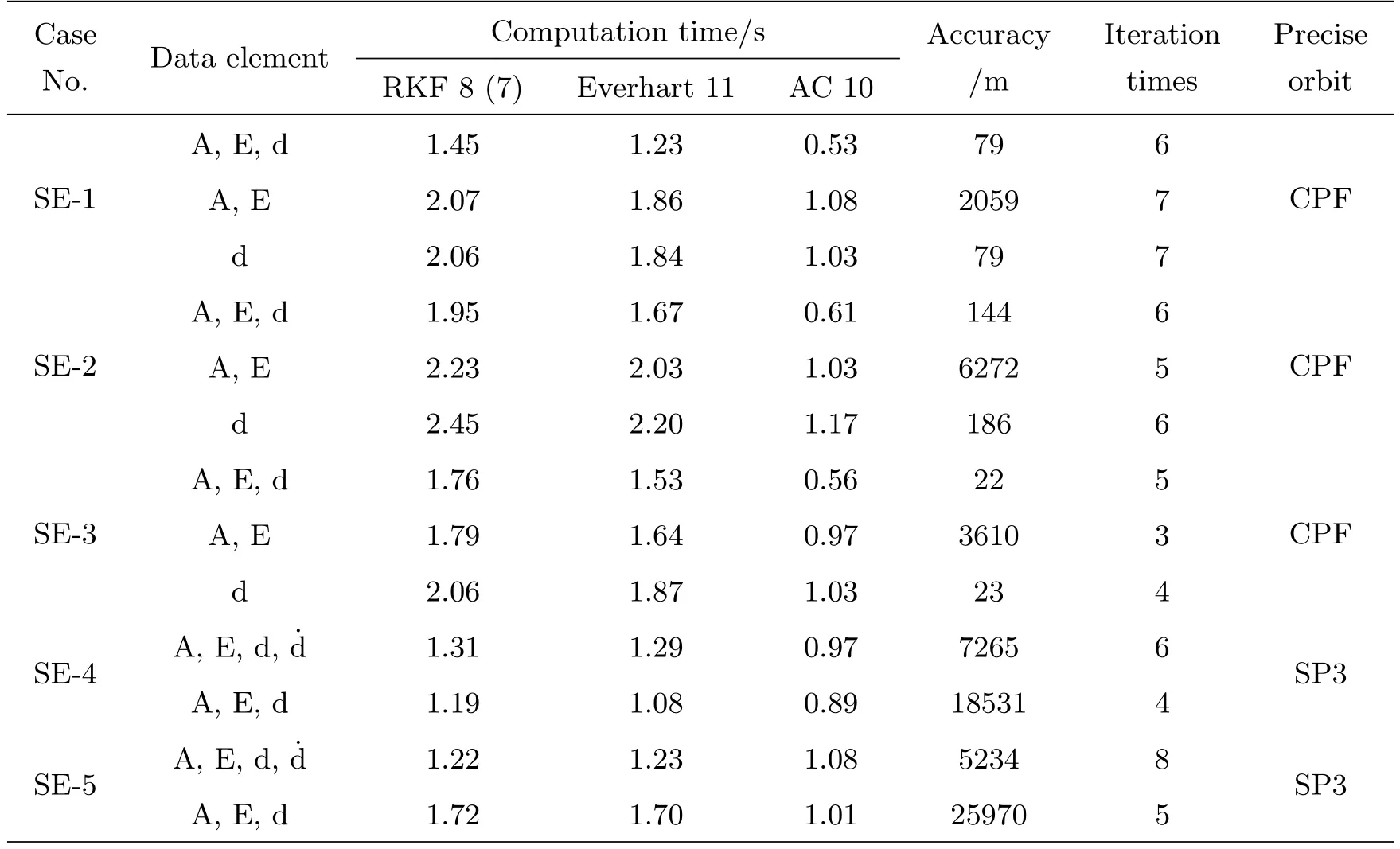
表2 SE定轨算例性能Table 2 Performance of SE orbit determination cases

表3 SE定轨的力学模型及公共参数Table 3 Force models and public parameters of SE orbit determination

算例1–5是较为典型的雷达获取空间碎片的数据条件, 数据的时间跨度约2–5 d, 每天能探测1–2次, 整体来说符合空间碎片稀疏性的特点. 稀疏数据条件下轨道改进收敛通常需要较多的迭代次数,由表2的统计结果可知以上算例在SPODFMD软件中的迭代次数为3–8次, AC、Everhart和RKF积分器的平均处理时间分别为0.91 s、1.62 s和1.78 s,积分器的计算效率以AC 10最佳, Everhart 11和RKF 8 （7）递次降低. AC积分器的高效众所周知, 然而可变步长的单步法积分器Everhart和RKF的计算效率接近AC积分器也是因为采用了先积分再插值的策略, 而星历精度的保障则主要归功于关键技术——非均匀插值基点构造方法的应用. 该方法可与任何一种单步法积分器结合使用, 达到兼顾各种偏心率轨道星历精度和计算效率的目的, 这一效果不论是定步长积分器AC还是变步长积分器逐点积分均不能实现.

数据条件是影响定轨精度的主要因素, 利用同一时刻获取多维资料中的不同元素及其组合定轨, 单站算例1–3仅利用了雷达测距元素的轨道改进收敛且定轨精度达到了百米甚至以下量级, 仅利用了雷达测角元素的轨道改进精度在公里级别, 同时利用测角和测距三元素的轨道改进精度不低于仅利用高精度测距元素的定轨精度;单站算例4–5针对高轨目标的雷达观测增加了测速元素, 仅利用测角或测距元素的定轨误差分别为25 km和18 km,增加高精度测速元素的融合定轨误差分别降至7 km和5 km.以上算例体现了高精度观测资料在单站轨道改进中发挥了决定性作用, 在各元素先验精度较为准确的情况下, 融合多维资料的轨道改进效果一般不逊于单维资料.

4.2 多源数据定轨

多源数据融合要求同一时间段内能获取到来自于不同设备的观测数据, 当组网观测或者协同观测时会产生多源数据融合定轨的需求. 以下用典型多站场景来测试软件的性能和融合效果, 表4列出了7个融合场景的数据特点, 表5为对应场景的定轨性能关键指标, 表6为主要的动力学模型及公共配置参数.

表4 多设备（ME）获取的数据资料Table 4 Data from Multi Equipment （ME）

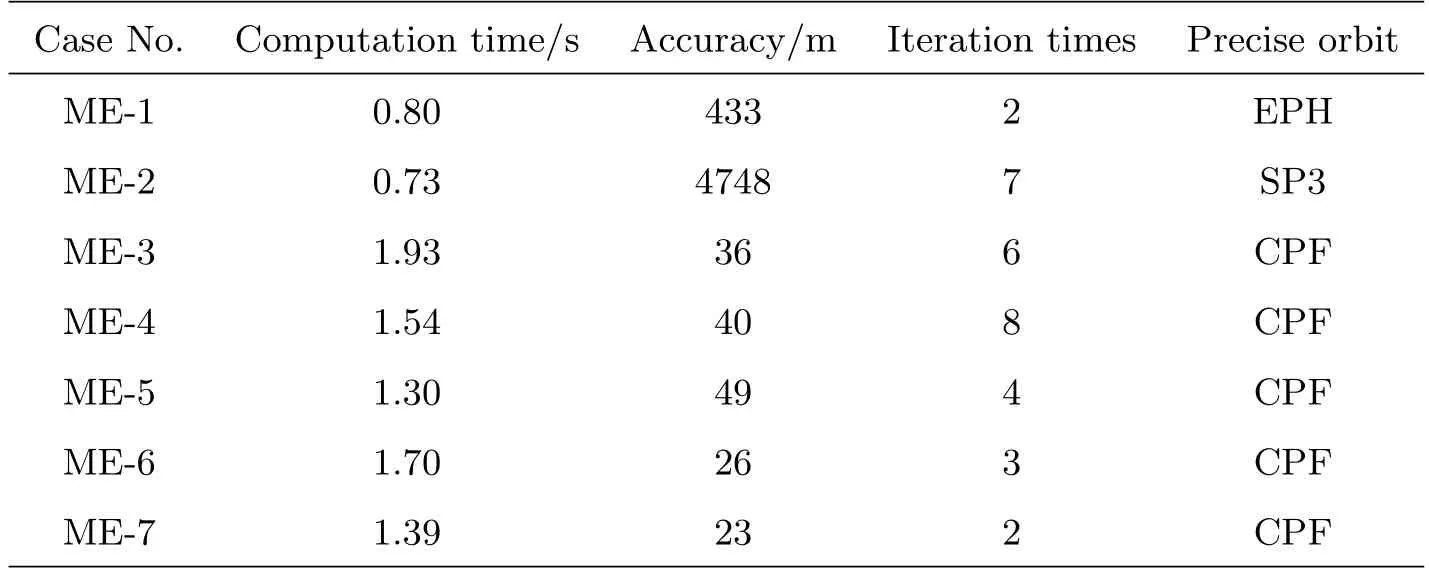
表5 ME定轨算例性能Table 5 Performance of ME orbit determination cases

表6 ME定轨的力学模型及公共参数Table 6 Force models and public parameters of ME orbit determination

表7 SPODFMD软件功能简述Table 7 Brief introduction of the software SPODFMD’s function

融合算例1–7展示了多源数据融合定轨的效果, 表5显示高轨目标37210利用1台天基光学和3台地基光学融合的精度达到了433 m, 相比利用单站雷达四元素资料7 km的定轨精度提高了一个量级以上; 高轨目标38091利用1台天基和1台地基光学的融合精度优于5 km; 低轨目标16908、7646和46469、1328和7647的融合精度均优于50 m.虽然依据以上少量算例不能直接得出多站融合精度高于单站的结论, 单从数值上分析, 融合的精度普遍高于单站, 这个提升主要由数据几何条件改善引起, 数据质量和数量是弱相关因素. 融合算例1–7利用AC积分器的平均计算时间为1.34 s, 虽然多站融合定轨处理的数据量相比单站有所增加, 但更加丰富的数据使得迭代次数减少, 总体而言计算时间仅有少许增加, 仍处于秒级水平.

4.3 动力学模型测试

SPODFMD软件支持70阶以内地球重力势及其偏导数的计算, 并可扩充附加潮汐、地球反照辐射压、行星引力等摄动力. 针对低轨目标7647和高轨目标37210, 图1和图2分别展示它们利用简约动力学模型和精密动力学模型进行轨道确定并预报轨道的位置误差（为表述方便, 由简约动力学模型定轨及预报的轨道称为F轨道, 由精密动力学模型定轨及预报的轨道称为P轨道）, 在定轨期内7647目标的F轨道与P轨道基本重合, 预报至2 d两者的偏差约50 m, 预报至6 d两者的偏差约230 m; 高轨目标37210整个定轨及预报期内F轨道与P轨道几乎重合. 在效率方面, 两个例子均显示利用了精密动力学模型的轨道改进时间相比利用简约动力学模型增加了约30%的计算时间. 已知编目目标的轨道更新频率约1–2 d 1次, 短期内简约动力学模型的定轨和预报精度与精密模型的差距不显著, 因此不推荐牺牲计算效率的精密动力学模型用于空间碎片编目定轨. 基于这一认知, SPODFMD软件在测试算例时, 均采用了简约的动力学模型, 配置方法如下: 低轨目标取地球引力场20×20阶, 中高轨目标取8×8阶, 地球重力势偏导数计算取4阶, 章动模型取4项, 考虑日月引力, 低轨目标考虑大气阻力, 高轨目标考虑太阳光压, 采用以上简约模型即可取得表2和表5中的定轨效果. 图1–2用于测试的精密动力学模型的配置如下: 低轨目标取地球引力场20×20阶, 中高轨目标取8×8阶, 地球重力势偏导数计算取4阶, 章动模型取108项, 考虑日月、行星引力和地球反照辐射压, 低轨目标考虑大气阻力和潮汐（海潮、固体潮、大气潮）, 高轨目标考虑太阳光压.

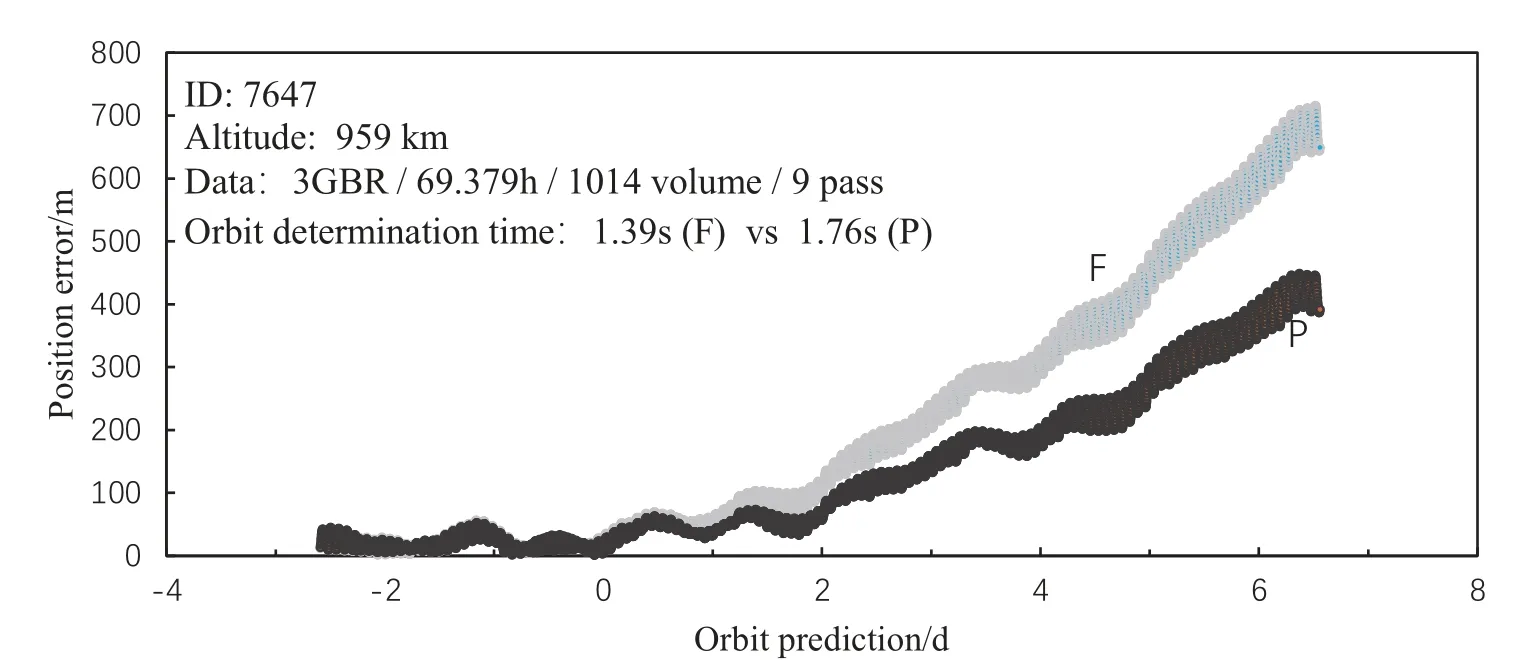
图1 低轨目标分别利用简约动力学模型和精密动力学模型定轨并预报轨道的位置误差Fig.1 Orbital position errors of a LEO object determined and predicted by using a simplified dynamic model and a precise dynamic model

图2 高轨目标分别利用简约动力学模型和精密动力学模型定轨并预报轨道的位置误差Fig.2 Orbital position errors of a GEO object determined and predicted by using a simplified dynamic model and a precise dynamic model

5 总结和展望

SPODFMD软件处理上述空间碎片典型多源融合算例的运算环境为:Windows 7; Inter Core i5-2400 CPU@3.10GHZ, 若采用主流i7及以上处理器,运算速度还有很大提升空间, 软件的定轨效率可以确切地说达到了秒级的水平, 在单台计算机上运行一天可执行约8万目标的编目定轨, 并行计算预计可管理数十万空间碎片, 在很长时间内轨道计算能力将不会成为空间监测组网的瓶颈. SPODFMD软件还是一款纯数值法定轨软件, 数值法的高精度特点已得到了国际国内同行的认可. 软件目前可针对14种主流设备获取的数据进行融合, 但尚不能涵盖所有的空间碎片观测设备, 下一步拟增加无线电测角测速、无线电时差频差设备类型以更好地适应多源数据融合的需求.