基于多层复杂网络的地铁系统脆弱性因素耦合分析

段晓红

(北方工业大学经济管理学院,北京 100144)

地铁作为城市交通的主动脉,它的安全稳定运行是城市安全管理水平的重要体现。然而,现代城市地铁线网密度大、覆盖范围广、客流强度高,在面临自然灾害、事故灾难、公共卫生事件、社会群体性事件等突发情况时,如果自身承载能力不足,将对城市交通系统产生巨大的影响,甚至威胁出行者的生命安全。因此,辨识地铁系统自身存在的脆弱性因素,明晰地铁系统脆弱性因素的耦合作用机理,对于实施科学精准的干预控制措施,并进一步提高地铁系统的本质安全水平至关重要。

近些年来,许多学者围绕地铁系统脆弱性开展了大量的研究。如:Avci等[1]基于关键性-脆弱性-影响性的风险分析模型,描述了地铁车站遭受威胁和脆弱性风险评估的通用程序,提出了缓解策略,并通过对比缓解策略实施前后的两次评估结果,验证了评估程序和缓解策略的有效性;宋英华等[2]针对公共汽车和地铁双层网络,选取最大联通子图比例、网络连通效率和网络效率3个指标,模拟计算与分析了城区内涝导致节点和连边失效情景下的双层交通网络脆弱性。

系统脆弱性的呈现是多个因素共同作用的结果,为此段晓红等[3]将两个或两个以上因素相互影响、相互作用导致系统脆弱性发生变化的现象定义为脆弱性因素耦合现象,并基于N-K模型量化分析了道路交通系统中多脆弱性因素的耦合效应;侯公羽等[4]在多因素耦合视角下分析了地铁施工安全系统的脆弱性,并从暴露性、敏感性和适应性三个方面选取地铁施工安全系统脆弱性因素,运用N-K模型识别了关键因素的耦合方式;Yan等[5]基于耦合的观点,选取城市排水管网脆弱性评价指标,并将熵权法和层次分析法相结合,构建了城市排水管网脆弱性评价模型;Xue等[6]为了识别山区公路交通事故多发路段,运用改进的经典耦合模型,揭示了风险因素的耦合机理,并计算了多风险因素的耦合度。

此外,还有一些学者将复杂网络理论引入地铁典型事件灾害链研究。如:王希良等[7]通过辨识地铁系统脆弱性干扰事件的链式影响关系,构建了干扰事件有向复杂网络模型,分析了网络结构特征,并基于互信息理论评估了网络节点的重要性,挖掘地铁系统脆弱性的关键干扰事件;Chen等[8]为了评估城市交通系统脆弱性,将灾害事件及其演化路径分别视为节点和边,构建了复杂网络模型,并提出了从微观和宏观两个层面量化节点、边和网络脆弱程度的措施。

复杂网络理论也适用于轨道交通事故致因分析。如:许未等[9]运用Apriori算法挖掘出铁路事故致因间的强关联规则,并基于复杂网络理论构建了以关联规则的提升度为边权的铁路事故致因网络,通过对网络结构特征的分析,把握事故发生的内在机理和规律;Zhou等[10]在识别事故-事故关系、致因-致因关系和事故-致因关系的基础上,构建了包含事故网络层、致因网络层及层间关系的双层地铁施工安全风险网络模型,并分析了网络的拓扑特征和鲁棒性。

通过分析已有文献可知,学者们对于地铁系统脆弱性因素及其耦合作用的研究较为丰富,部分学者探讨了复杂网络理论在事故链和致因分析等安全风险领域的应用,为本文研究提供了借鉴,但目前尚未见有学者在复杂网络视角下分析地铁运营脆弱性因素的耦合作用,更未拓展到多层网络分析视域。事实上,地铁系统脆弱性因素间存在多种耦合模式,与传统耦合模型相比,多层网络理论能够更加准确地反映地铁系统脆弱性因素间的多重耦合关系,并能从多维度、多层面分析和明确地铁系统脆弱性因素间的相互作用机理。因此,本文拟在地铁系统脆弱性因素辨识的基础上,以不同网络层表征地铁系统脆弱性因素间不同的耦合模式,构建了描述因素耦合关系的多层网络模型,并通过辨识网络中的关键节点和连接,来把握地铁系统脆弱性的形成机理和规律,明确实施安全管理的关键位置和环节。

1 地铁系统脆弱性因素耦合分析模型构建

1.1 地铁系统脆弱性因素辨识

脆弱性是系统及其组成要素易于受到扰动的影响和破坏,并缺乏抵抗干扰及恢复初始状态的能力[3]。事故致因理论认为,事故的发生是由人的不安全行为、物的不安全状态、环境和管理缺陷四类因素作用的结果。事故是系统脆弱性的外在体现,本研究借鉴事故致因理论的观点,并结合相关文献[3-5]中对脆弱性因素的分类方法,从人-机-环-管四个方面出发,识别地铁系统脆弱性的影响因素。

首先,通过文献[11-15]分析遴选出28项脆弱性因素;然后,对1969—2021年间国内外199起(国内131起,国外68起)地铁安全事故案例进行致因分析,提取引发每一起事故的致因关键词,并逐一对应为脆弱性因素;最后,剔除199起地铁安全事故中未涉及的8项脆弱性因素,最终获得的地铁系统脆弱性因素,见表1。

表1 地铁系统脆弱性因素

地铁安全事故案例来源于文献资料[16-19]、新闻报道和地铁官方通报(包括各城市地铁官方网络平台、微博官方公众号等),三种来源所占比例分别为68%、19%和13%,其中均包含对事故原因的详尽分析。根据事故性质将199起地铁安全事故划分为8种类型,各种类型事故的数量见表2。

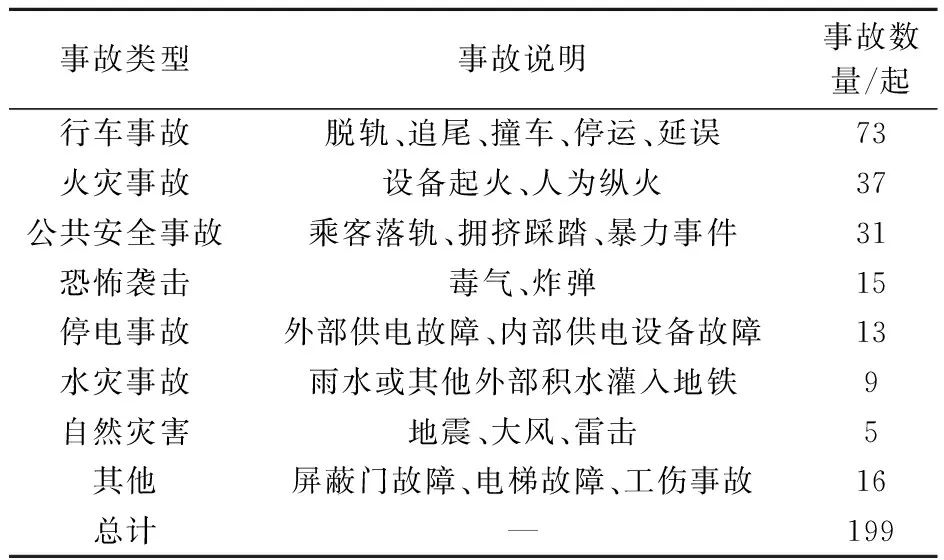
表2 地铁安全事故类型和数量

根据概念内涵和分析模型,系统脆弱性具有暴露性、敏感性和适应性3个特征要素。

暴露性强调系统暴露于扰动中的程度,取决于系统遭受威胁的几率和强度。在地铁系统中,人员不安全行为、乘客人为破坏等违规违章行为,地震等自然灾害,暴雨、雷电、大风等恶劣天气,大客流、外物入侵等外部环境异常,以及安全防范措施不足、安全与质量监管不到位等管理因素均会增加地铁系统处于威胁中的程度,因此归类为暴露性因素。

在同样的暴露条件下,敏感性刻画了系统受到不利影响的难易程度,与系统对于威胁的反应时间、反应幅度和反应限度相关。在地铁系统中,人因失误、人员安全意识薄弱、员工业务水平低等因素使人员在面对威胁时无法做出及时有效的反应,造成地铁系统敏感性的增加。尤其是地铁在出现供电系统故障、车站设备故障、车辆故障、信号系统故障、隧道和线路被破坏等系统自身故障时,外部扰动的作用更易对地铁系统产生不利的影响,因此将其归类为敏感性因素。此外,设计施工缺陷、设备检修不及时等设施设备的不利因素也将导致地铁系统敏感性的增加。

当系统在扰动影响下已经出现功能的改变时,适应性则描述了系统具有自我调节和恢复到可用功能的能力。在地铁系统中,与事件应急响应相关的人员应急处置能力,消防、应急照明等安全设备,应急救援水平等管理因素,直接影响地铁系统自身的适应和恢复能力,因此将其归类为适应性因素。

根据上述分析,并借鉴文献资料中的归类方法,将表1中因素纳入到地铁系统脆弱性的特征要素中,构建了地铁系统脆弱性层级分析体系,如表3所示。

表3 地铁系统脆弱性因素层级分析体系

1.2 地铁系统脆弱性因素耦合模式分析

1.2.1 地铁系统脆弱性因素耦合的概念和类型

系统脆弱性的呈现不是单一因素作用的结果,而是由多种因素共同作用导致的。将两个或两个以上脆弱性因素相互影响、相互作用导致地铁系统脆弱状态发生变化的现象定义为脆弱性因素耦合现象[3]。对脆弱性因素耦合作用的关注,扩大了地铁系统脆弱性的研究范畴。

对于特征要素层,根据参与耦合的要素数目不同,将特征要素耦合作用导致的地铁系统脆弱性分为以下2种耦合作用模式:

1) 双要素耦合系统脆弱性,指因两个特征要素之间相互依赖和共同作用而导致的地铁系统脆弱性,包括暴露性-敏感性耦合、暴露性-适应性耦合、敏感性-适应性耦合3种耦合方式。

2) 三要素耦合系统脆弱性,指因三个特征要素之间相互依赖和共同作用而导致的地铁系统脆弱性,包括暴露性-敏感性-适应性耦合1种耦合方式。

对于脆弱性因素层,根据参与耦合的因素数目不同,将脆弱性因素耦合作用导致的地铁系统脆弱性分为19种耦合作用模式。

1) 双因素耦合系统脆弱性,指因两个脆弱性因素之间相互依赖和共同作用而导致的地铁系统脆弱性,包括人因失误-人员不安全行为耦合、人因失误-人员安全意识薄弱耦合等190种耦合方式。

2) 三因素至十九因素耦合系统脆弱性,指因3个及以上脆弱性因素之间相互依赖和共同作用而导致的地铁系统脆弱性,包括人因失误-人员不安全行为-人员安全意识薄弱耦合、人因失误-人员不安全行为-人员安全意识低-人员业务水平低耦合等1 048 364种耦合方式。

1.2.2 基于N-K模型的耦合度计算

N-K模型最初由Kauffman提出,适用于量化分析复杂系统中组件之间的相互依赖程度。N-K模型具有N和K两个关键参数,N表示系统拥有组件的总数,K表示系统中具有相互依赖关系的组件个数,其取值为0～N-1。第n(n=1,2,…,N)个组件有On种状态可取。脆弱性因素的耦合作用使系统状态达到突变阈值时,地铁系统遭受破坏而导致事故的发生。系统中因素间在某种组合方式下引发事故的概率越高,则这些因素耦合得到的值就越大。

利用N-K模型衡量N个因素f1,f2,…,fn,…,fN之间的耦合作用程度,即耦合度T为

T(f1,f2,…,fn,…,fN)=

(1)

式中:Pon表示当第n个因素处于第on种状态时事故发生的概率;Po1,o2,…,on,…,oN为第1个因素的第o1种状态、第2个因素的第o2种状态、依次类推第n个因素的第on种状态、第N个因素的第oN种状态耦合作用时事故发生的概率。

1.3 地铁系统脆弱性多因素耦合网络模型构建

在传统单层网络模型的基础上,多层网络更强调复杂系统中的异质性,这包括对节点及其作用关系的异质性、层间节点之间作用模式的探讨与刻画。运用多层网络模型能够更为系统、全面地描述系统脆弱性因素之间的多重耦合作用关系。

多路复用网络考虑了同一组节点间关系的异质性,是多层网络的一种。该网络的每一层包含相同的一组节点,不同网络层描述节点间的不同关系或相互作用模式,将不同网络层中的相同节点对应相连,就形成了网络的层间连边。网络的数学模型如下:

利用超邻接矩阵G=(A,B)表示包含L层的复用网络,其中A={A[1],A[2],…,A[α],…,A[L]}为第α(α∈{1,2,…,L})层网络的邻接矩阵A[α]所组成的集合,B={B[1,2],B[1,3],…,B[α,β],…}为第α层与第β(β∈{1,2,…,L},β≠α)层的层间网络邻接矩阵B[α,β]所组成的集合[20]。

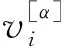
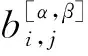
地铁系统脆弱性的特征要素存在两种耦合作用模式,脆弱性因素也包含19种耦合作用模式,针对特征要素和脆弱性因素分别构建多路复用网络模型,其中不同网络层代表要素或因素间的不同耦合作用模式。该模型不仅包含单层网络的全部信息,而且关注不同耦合类型间的异质性,每一层网络刻画一种耦合作用模式(包括双因素耦合、三因素耦合等),更符合多因素耦合分析的基本逻辑,有利于厘清因素间的耦合机理,把握耦合演化路径,进而实施分层分类的精细化预警和控制。

1.3.1 地铁系统脆弱性特征要素耦合网络模型构建

地铁系统脆弱性具有暴露性、敏感性和适应性三个特征要素,它们之间存在双要素耦合和三要素耦合两种耦合作用模式。将特征要素作为节点,每一层网络表征特征要素间的一种耦合作用模式,构造双层网络模型GC=(AC,BC),其中第一层网络分析双要素耦合作用关系,第二层网络分析三要素耦合作用关系。网络的超邻接矩阵为

(2)

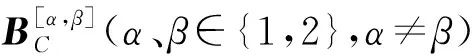
在特征要素耦合多路复用网络中,不考虑层间不同特征要素间的作用关系,故层间网络邻接矩阵为

(3)

N-K模型所需数据来源于国内外199起地铁安全事故的致因分析。一起事故中,若某一特征要素发生,其状态定义为1,否则为0。运用N-K模型计算h1、h2、h3三要素各类型耦合度的具体步骤如下:

1) 统计计算h1、h2、h3耦合发生次数和频率。将h1、h2和h3视为系统脆弱性的三个组件,各组件具有0和1两种状态,统计h1、h2、h3所有可能状态组合的发生次数和频率,其结果见表4。

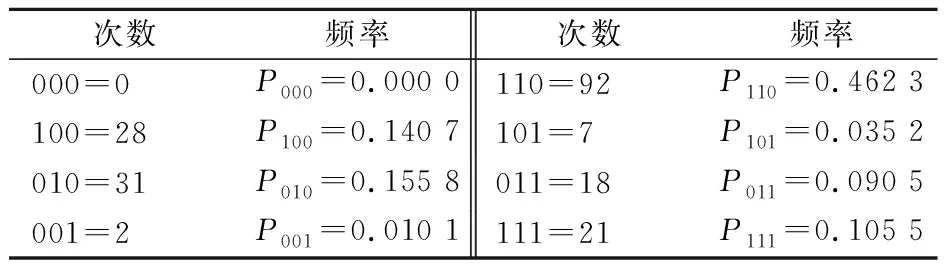
表4 h1、 h2、 h3耦合发生次数和频率

2) 计算各类型耦合相关概率。单要素耦合发生次数为0..=000+010+001+011=51,则单要素耦合相关概率为P0..=51/199=0.256 3,同理求得P1..=0.743 7、P.0.=0.185 9、P.1.=0.814 1、P..0=0.758 8、P..1=0.241 2。双要素耦合发生次数00.=000+001=2,则双要素耦合相关概率为P00.=2/199=0.010 1,同理求得P01.=0.246 2、P10.=0.175 9、P11.=0.567 8、P0.0=0.155 8、P0.1=0.100 5、P1.0=0.603 0、P1.1=0.140 7、P.00=0.140 7、P.01=0.045 2、P.10=0.618 1、P.11=0.196 0。

3) 计算各类型耦合度。由式(1)可知,h1、h2、h3三要素耦合度为

log2(Pt1,t2,t3/(Pt1..×P.t2.×P..t3)]=0.088 0

(4)

h1、h2双要素耦合度为

log2(Pt1,t2,./(Pt1..×P.t2.)]=0.044 8

(5)

同理求得:

T(h1,h3)=0.029 0,T(h2,h3)=0.000 0

由此获得第α(α=1,2)层网络的邻接矩阵为

(6)

(7)

特征要素耦合双层网络的结构示意图,如图1所示。

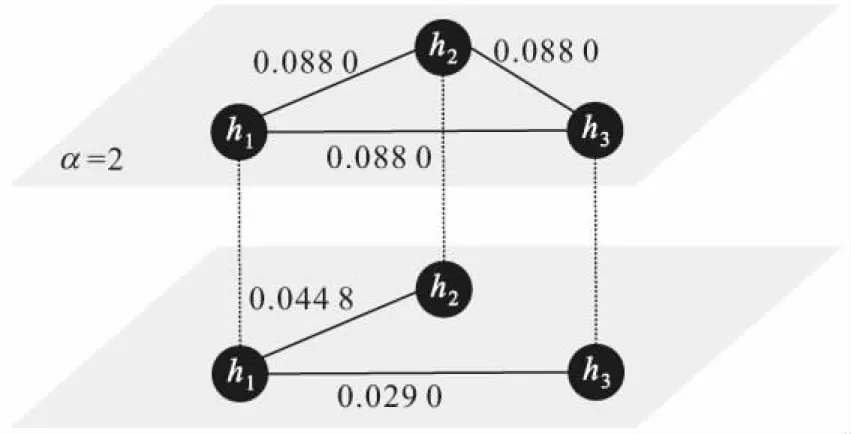
图1 特征要素耦合双层网络结构示意图Fig.1 Diagrammatic sketch of characteristic elements coupling bilayer network

1.3.2 地铁系统脆弱性因素耦合网络模型构建

地铁系统脆弱性因素层包含20个因素,它们之间存在双因素耦合、三因素耦合、以此类推直至二十因素耦合等多种作用模式。将脆弱性因素作为节点,每一层网络表征脆弱性因素间的一种耦合作用模式,构造19层网络模型GD=(AD,BD),其中第一层网络分析双因素耦合作用关系,第二层网络分析三因素耦合作用关系,以此类推第19层网络分析20因素耦合作用关系。网络的超邻接矩阵为

(8)

在脆弱性因素耦合多路复用网络中,不考虑层间不同因素之间的作用关系,故层间网络邻接矩阵为

(9)

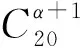
Fq=(Rq,Sq,Wq) (q=1,2,…,Q)

(10)

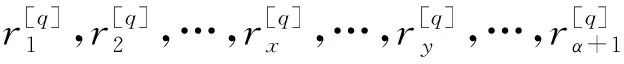
(11)

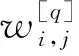
(12)

基于国内外199起地铁事故的致因分析,计算两两脆弱性因素间的耦合关系强度,具体步骤如下:

1) 将因素r1,r2,…,r20视为地铁系统脆弱性的20个组件,统计双因素、三因素、直至二十因素的不同耦合方式下发生事故的频率,并以此度量该耦合方式的耦合度。根据统计数据,本案例存在双因素耦合至六因素耦合5种作用模式,表5中列出了地铁系统脆弱性因素排名前五的耦合方式及其耦合度。

表5 地铁系统脆弱性因素排名前五的耦合方式及其耦合度

2) 对于第α(α=1,2,…,5)层网络,利用α+1阶完全图描述α+1因素耦合关系,并利用式(11)和(12)计算两两脆弱性因素间的耦合关系强度。地铁系统各网络层中排名前三的脆弱性因素及其耦合关系强度见表6,地铁系统脆弱性因素耦合多层网络的结构示意图见图2。鉴于图的可读性,仅标识耦合关系强度排名前六的连边及其权重,并忽略了层间相同节点之间的连边。

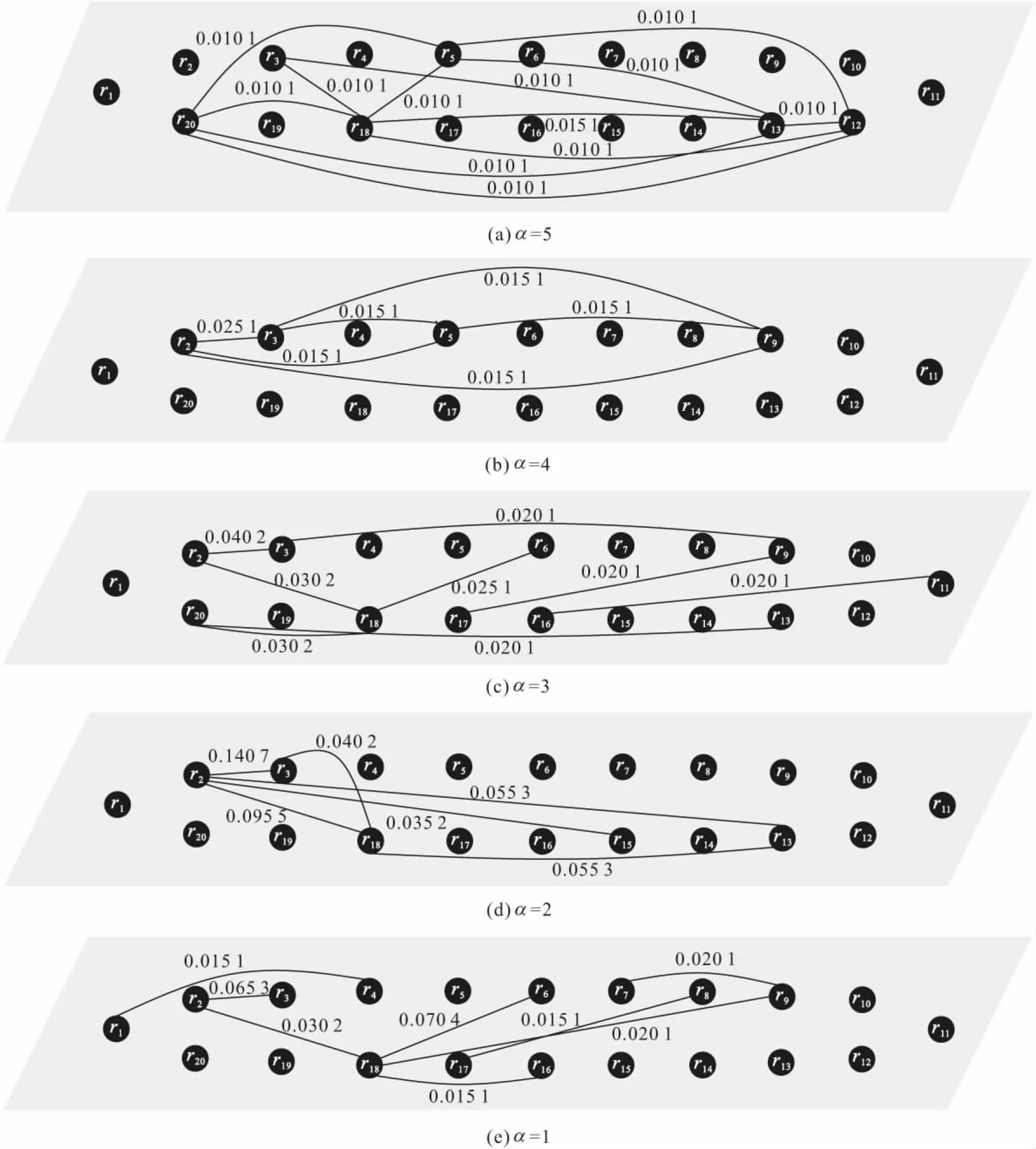
图2 地铁系统脆弱性因素耦合多层网络结构示意图Fig.2 Diagrammatic sketch of subway system vulnerability factors coupling multi-layer network

表6 地铁系统各网络层中排名前三的脆弱性因素对及其耦合关系强度

由图2可知:人因失误-员工业务水平低(r1-r4)、供电系统故障-车辆故障(r7-r9)、车站设备故障-设备检修不及时(r8-r17)、外物入侵-安全防范措施不足(r16-r18)在双因素网络中耦合关系强度较高,但当因素数目增加时,耦合效果不再显著,表明这四组因素往往以双因素耦合的形式存在(即为单一耦合形式),应重点对该耦合作用模式进行解耦控制;与此不同,人员不安全行为-人员安全意识薄弱(r2-r3)、人员不安全行为-安全防范措施不足(r2-r18)、乘客人为破坏行为-安全防范措施不足(r6-r18)在其他网络层中的耦合作用也相对明显,表明这三组因素呈现出多样化的耦合形式(即为复合耦合形式),因此在控制双因素耦合的同时,还需要持续监控其他因素出现的可能性,以防止更多因素参与耦合而导致脆弱性的增加。

同理,通过逐层分析地铁系统脆弱性因素间的耦合机理,形成的脆弱性因素分层分类控制策略见表7,地铁系统脆弱性各网络层中点度值排名前五的节点见表8。

表7 地铁系统脆弱性因素分层分类控制策略

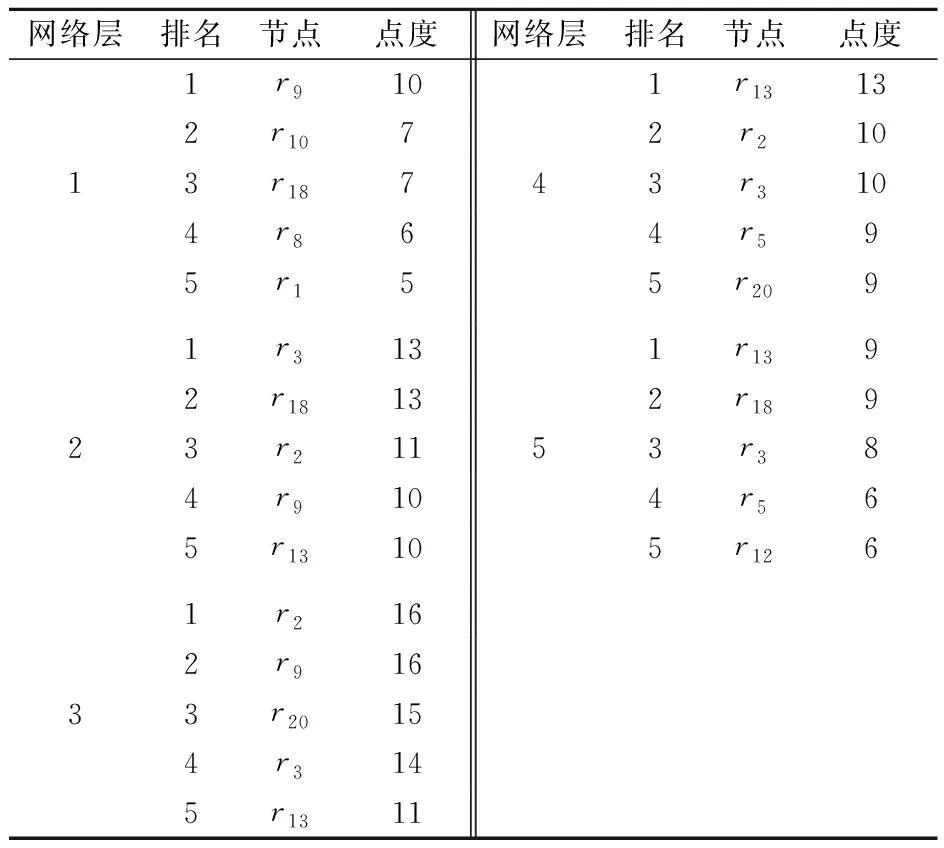
表8 地铁系统脆弱性各网络层中点度值排名前五的节点

由表8可知:地铁系统各网络层中有11个节点具有较高的点度值,说明与它们发生耦合的节点数目较多,是各网络层中的关键控制节点;进一步分析发现,人员安全意识薄弱r3、设计施工缺陷r13、车辆故障r9、安全防范措施不足r18、人员不安全行为r2、应急救援水平低r20、应急处置能力差r5在多个网络层中均为关键节点,对它们实施重点防控能够避免因素间复杂耦合作用的发生,从而有效降低地铁系统的脆弱性。

2 地铁系统脆弱性多因素耦合网络中关键节点和连接识别

2.1 聚合多层网络

将多层网络中各层所包含的所有节点和连接根据一定规则聚合到一个单层网络中,构成聚合多层网络。多路复用网络的每一层具有相同的节点,且不考虑层间不同节点的联系,因此可基于以下规则构造聚合多层网络:

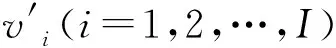
(13)

2.2 边的影响力度量

网络中边的影响力不仅取决于其端点之间的关联强度,还与邻接节点的重合度相关。若某条边的两个端点拥有更多相同的邻接节点,则它们之间的联系更加紧密,连接两者的边也具有更高的影响力。通常采用影响系数表征边的影响力,并运用Jaccard相似度加以衡量,由此将聚合多层网络中边ei,j′=(vi′,vj′)的影响系数定义为[21]

(14)

式中:Mi和Mj分别表示节点vi′和vj′的邻接节点所构成的集合;Mi∩Mj为Mi和Mj的交集;Mi∪Mj为Mi和Mj的并集,但不包括vi′和vj′本身;符号||表示集合中元素的个数。

2.3 节点的影响力度量

将节点的度中心性和K核分解法相结合,并综合考虑聚合多层网络中边的影响系数θi,j和权重ai,j′,定义多层加权度用以衡量节点的影响力[21]。节点的多层加权度计算公式为

(15)

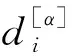
在计算节点的多层加权度值时,采用K核分解法的基本步骤为:①计算所有K核值最小节点的多层加权度值;②删除完成计算的节点及其连边,计算当前网络中K核值最小节点的多层加权度值;③重复步骤②,直至完成所有节点的计算。

2.4 特征要素耦合网络中关键节点和连接识别

将特征要素耦合网络GC聚合为单层网络GC′,根据式(13)计算得到GC′的邻接矩阵AC′为

(16)

根据式(14)计算得到聚合多层网络中边的影响系数矩阵为

(17)

根据式(15)计算得到特征要素耦合网络中节点影响力,见表9。

表9 特征要素聚合多层网络中节点的影响力

分析上述特征要素耦合网络的量化结果可知:

1) 特征要素间耦合度T(h1,h2,h3)>T(h1,h2)>T(h1,h3)>T(h2,h3),说明三要素共同发生时地铁系统脆弱性更加明显;对于双要素耦合效应,暴露性和敏感性的耦合作用效果最为显著,地铁安全管理人员应重点关注这两个要素同时发生的情况。

2) 暴露性节点的影响力最高,因此最为关键,敏感性次之,适应性最低,这与暴露性节点与其他两个节点均存在耦合效应且耦合强度较高相关。对表3中地铁系统暴露性的7个影响因素加以控制,能够从根本上减少地铁系统与外部扰动的联系,从而降低扰动对地铁系统的不利影响,这也体现出在地铁安全管理工作中,“防”比“救”更加重要。

2.5 影响因素耦合网络中关键节点和连接识别

将影响因素耦合网络GD聚合为单层网络GD′,根据式(13)计算得到GD′的邻接矩阵,其中影响因素聚合多层网络中元素值排名前五的边及其关系强度,见表10。

表10 影响因素聚合多层网络中边及其关系强度

根据式(14)计算得到边的影响系数,其中影响因素聚合多层网络中排名前五的边及其影响系数,见表11。

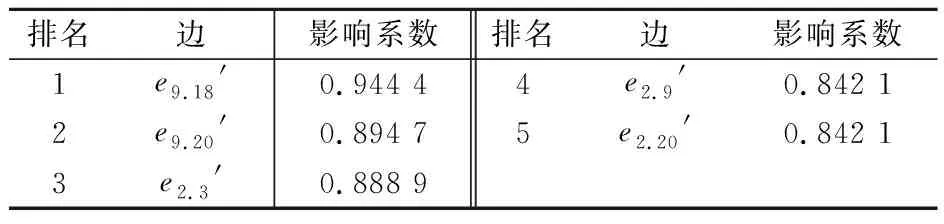
表11 影响因素聚合多层网络中排名前五的边及其影响系数

根据式(15)计算得到影响因素聚合多层网络中节点的影响力,其结果如表12所示。

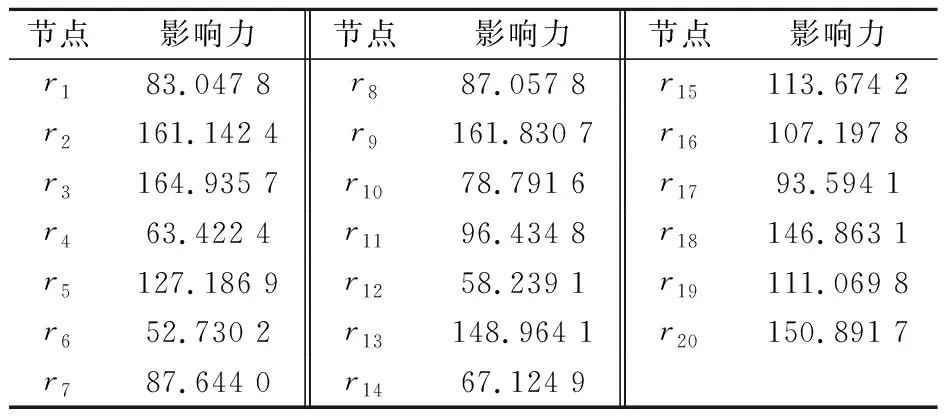
表12 影响因素聚合多层网络中节点的影响力

分析上述影响因素耦合网络的量化结果可知:

1) 从聚合多层网络中边的关系强度(表10)来看,人员不安全行为-人员安全意识薄弱耦合、人员不安全行为-安全防范措施不足耦合、乘客人为破坏行为-安全防范措施不足耦合的关系强度最高,这说明它们是脆弱性因素间的重要耦合作用方式,对地铁系统脆弱性的影响最为显著。进一步分析上述连边在各层网络中的情况,结果显示:人员不安全行为-人员安全意识薄弱耦合在双因素至五因素网络层中关系强度均排名前三,可见其在多种耦合作用模式下均为关键连接;人员不安全行为-安全防范措施不足耦合在双因素至四因素网络层中关系强度位居前三;乘客人为破坏行为-安全防范措施不足耦合仅在双因素网络层中关系强度排名前三。

2) 从聚合多层网络中边的影响系数(表11)来看,车辆故障-安全防范措施不足耦合、车辆故障-应急救援水平低耦合、人员不安全行为-人员安全意识薄弱耦合的连边具有最高的影响系数,说明它们拥有更多共同的邻居节点,因而更易相互影响。其中,人员不安全行为-人员安全意识薄弱耦合同时具有最高的关系强度,说明地铁系统脆弱性呈现时这两个因素往往同时发生,且与其中之一存在耦合关系的影响因素往往与另一因素也存在联系,同时也说明人员不安全行为-人员安全意识薄弱耦合是地铁系统最为关键的耦合作用模式,地铁安全管理部门应优先加以关注和控制。

3) 在多层耦合关系网络的视角下,人员安全意识薄弱、车辆故障和人员不安全行为的影响力最高,是地铁系统最为关键的脆弱性因素,它们分属于人的敏感性因素、机的敏感性因素和人的暴露性因素。因此,地铁安全管理部门应通过监控、培训、宣传、奖惩等手段逐步提高员工和乘客的安全意识,杜绝员工违规违章操作、超速驾驶、疲劳驾驶以及乘客跨越黄线、拥挤车门电梯、抢上抢下等人员不安全行为,并通过加强技术培训、提高车辆故障监测和处理技术水平、科学制定并严格落实车辆检修制度、强化外协维修管理等手段减少车辆故障,同时确保车辆故障的及时排除。

3 结 论

本研究的创新之处在于,在复杂网络和因素耦合视角下分析地铁系统脆弱性,拓宽了地铁系统脆弱性研究的理论视角。鉴于单层网络难以表征多种耦合类型,遵循多因素耦合分析的基本逻辑,引入多层网络理论,面向不同类型剖析脆弱性因素间耦合作用机理和演化路径,并兼顾聚合多层网络的整体特征和各网络层的局部特征,识别实施防控的关键因素和耦合方式,探索了分析和量化多因素耦合的新方法,为地铁风险预控和应急处置提供了理论与决策依据。

本研究的主要发现在于:①根据各网络层中脆弱性因素间的耦合作用机理和强度,得出不同耦合类型下的关键因素和耦合方式,如车辆故障、信号系统故障等是双因素网络中的关键因素,人因失误-员工业务水平低、供电系统故障-车辆故障等是该网络层的关键耦合方式;②根据关键耦合方式在不同网络层中分布的差异性,将其划分为单一耦合形式和复合耦合形式两种类型,并形成分层分类的脆弱性控制方案,如人因失误-员工业务水平低为单一耦合形式,可重点控制双因素耦合现象,而人员不安全行为-人员安全意识薄弱在双因素至五因素耦合网络中均存在且为关键连接,属于复合耦合形式,需持续监控其他因素存在的可能性;③综合聚合多层网络中边的连接强度和影响系数,暴露性-敏感性耦合、人员不安全行为-人员安全意识薄弱耦合是地铁系统脆弱性的关键耦合作用方式;④根据节点影响力分析结果,暴露性是地铁系统关键特征要素,人员安全意识薄弱、车辆故障、人员不安全行为则是地铁系统关键脆弱性因素;⑤与传统的单层网络和N-K模型相比,本文模型能够获得多维度、多层面的分析结果,且更具可读性和可操作性,因而更适于系统指导地铁安全管理工作,而基于地铁实际事故案例开展研究,分析结果符合地铁事故发生的内在机理和规律。

本研究今后的优化方向为:更新事故案例库并据此持续优化模型,使其更加客观地反映实际;本文耦合模型为无向加权网络模型,下一步研究中需关注耦合影响的方向性。

致谢:特别感谢北方工业大学信息学院周翰霖同学对本研究中数据处理和模型验证相关工作的协助。