面向低碳的退役农机多目标拆解序列规划研究
2023-10-09冯广圣杨永发
焦 洁, 冯广圣*, 袁 刚, 杨永发
(1.南京林业大学人文学院,江苏 南京 210037;2.东南大学机械工程学院,江苏 南京 211102;3.西南林业大学机械与交通学院,云南 昆明 650224)
随着复杂农机产品机械化、智能化、精准化的快速发展,以及农机产品生命周期的缩短,退役的农机产品大量产生,对其拆解的难度也日趋增加,具体表现为农机产品的拆解变得更频繁、零部件种类及数量众多、结构组织庞杂、拆解要素间存在空间、时间上的多重耦合等特点,对退役农机产品拆解方案的设计提出了新要求。 退役农机产品不仅含有电子元器件等对人体有害的零部件,而且蕴藏着大量的可再生资源,若不能有效地再生利用,将是对资源的极大浪费。 产品回收利用及其再制造已列入国家“十三五”节能减排领域的战略性新兴产业,同时国家“十四五”循环经济发展规划也强调废旧物资循环利用体系构建,对实现双碳目标和促进生态文明建设具有重要意义。
当前国内外学者对产品拆解规划进行了大量研究,其研究重点主要是确定性范畴问题,其研究假定各个零部件是完全可拆解,根据拆解工艺、拆解效率等展开产品可拆解性分析。 例如,Yang Y S 等[1,2]对废旧农机产品进行了多属性评价,提出了基于DEA 效率评估的可拆解性评估模型。 周亮等[3]基于拆装过程的稳定性并结合与或图实现了拆解序列规划。 张雷等[4]对产品结构关系信息表达实现了拆解序列规划。 Zussman 等[5]运用自适应算法实现了拆解序列优化。 Kongar 等[6]以产品的拆解时间最短、拆解方向变化次数最小及方向变化角度参数的变化最小等综合参数作为目标实现了拆解序列的决策研究。 Tian等[7,8]提出应用分散搜索和人工蜂群算法以最大化拆解收益和最小化拆解时间进行了最优拆解序列的决策。 考虑到拆解过程的不确定性特征,一些学者对不确定性产品拆解问题进行了研究。 Grochowski 等[9]针对不确定拆解规划问题提出了一种基于机器学习的求解方法。 陈伟达等[10,11]基于模糊理论进行了不确定条件下拆解序列规划研究。 Zhang Z 等[12,13]提出了基于模糊时间特征的可拆解性设计方法。
对于多目标拆解规划求解问题,一些学者提出了基于启发式算法进行求解计算。 蔡宁等[14]考虑能耗,建立多目标拆卸线平衡优化模型。 朱卓悦等[15]提出了一种多目标蚁群算法用于求解拆解效率和拆解危害的集成优化模型。 张则强等[16]提出了基于随机作业时间的U 型拆卸线平衡多目标优化模型。 Ren 等[17]提出一种多目标顺序相依拆卸线平衡模型,并设计一种自适应进化的变邻域搜索算法用于求解构建模型。 张雷等[18]提出一种基于环形拓扑结构的花授粉算法,求解得到了碳排放与收益的随机并行拆卸线平衡最优解。 脱阳等[19]提出一种改进樽海鞘群算法用于求解可变时间的双边机器人拆卸线平衡问题,通过汽车拆解案例验证了所提算法的可行性和高效性。 为了灵活高效地完成再制造中的拆卸过程,Xu W J 等[20]采用改进的基于Pareto 的离散蜜蜂算法求解人机协作的拆解规划问题。 王书伟等[21]提出变邻域蛙跳算法用于解决工作站数量确定的双边拆卸线平衡问题。 Liang J等[22]建立了基于概率的任务破坏性双边拆卸模型,结合扁虫算法的再生过程实现大型产品的双边拆解线平衡。 Singh R K 等[23]提出了一种新的平衡量子启发进化算法来优化拆解线平衡问题的利润和工作负载平衡。
通过以上分析可知,目前有关拆解规划的研究主要以拆解效率和经济性为目标函数。 随着当前对双碳目标的关注度越来越高,有必要引入以拆解碳排放为优化目标的拆解规划问题。 因此,本研究将拆解时间、拆解费用和拆解碳排放共同引入到废旧农机拆解规划问题之中,在满足拆解经济性和效率的同时,还可为废旧产品绿色拆解工艺设计及选择提供决策支持。
1 果蝇算法原理
果蝇优化算法因其参数变量少、求解计算快、寻优能力强等优点,已广泛应用于工程领域非线性问题求解。 果蝇算法的主要逻辑是模仿果蝇觅食过程的寻优行为,通过果蝇个体的嗅觉操作寻找食物气味浓度高的地方,再通过果蝇群体的视觉操作找到食物源具体位置,并通知其他群体飞向食物源位置。果蝇算法的逻辑步骤如下:
步骤1:种群初始设置参数。 种群初始化并设置参数,如种群规模,最大迭代次数,果蝇开始搜索位置 (X-axis,Y-axis) 。
步骤2:嗅觉操作。 果蝇个体通过嗅觉操作遍历SN 个位置,假设果蝇在嗅觉操作过程中选择随机方向和距离搜索食物,则个体位置公式如(1)所示。
其中,Randomx,Randomy为随机值;X-axis为个体初始横坐标;Y-axis为个体初始纵坐标。
步骤3:味道浓度计算。 果蝇个体间通过与原点的距离得到味道浓度判定值Si,然后得到味道浓度semlli,其计算公式如式(2)。
步骤4:根据气味浓度值,寻找味道浓度最高的位置。
步骤5:视觉操作。 果蝇通过视觉找到食物浓度最佳的位置,保留最佳浓度值及位置。
步骤6:判断是否达到算法终止条件,若g =max_gen,则算法结束,否则,重复步骤2 至步骤5,直到满足终止条件。
2 数学模型构建
退役农机产品拆解过程中会受到产品几何约束,失效程度等限制,拆解人员需要结合产品结构特征构建Petri 网,然后根据拆解优先关系实施拆解活动。 因此,结合农机产品特征,本研究提出一种多目标拆解序列规划模型,即考虑拆解时间、拆解成本、拆解碳排放,从而建立退役农机多目标拆解规划模型。
根据上述问题描述,结合农机拆解过程中最小时间、最小成本和最小碳排放目标函数,构建的多目标数学模型如下:
其中,公式(7)、(8)和(9)分别表示最小拆解时间,最小拆解成本和最小碳排放函数;j 为任务编号;m 是工作站编号;表示任务j 在机械m 上的拆卸时间;为机械m 的空闲时间;ej为任务j 的单位碳排放;cj为任务j 的单位拆卸成本;c0表示单位待机成本;CT 为节拍时间;Xjm,Ym为二元变量。
3 结果与分析
以某型号拖拉机变速器拆解为例,将本文提出的模型和算法进行应用验证。 拖拉机变速器三维结构图如图1 所示。 表1 给出了拖拉机变速器的拆卸实验的相关信息,包括拆卸方向、紧前任务、拆卸时间、零件需求量。 拆解时间选取实际操作的作业时间,部件对应的拆卸时间成本根据企业实际情况进行评估,变速器几何中心选为坐标原点,采用三维坐标法进行标注。

表1 拖拉机变速器拆卸信息
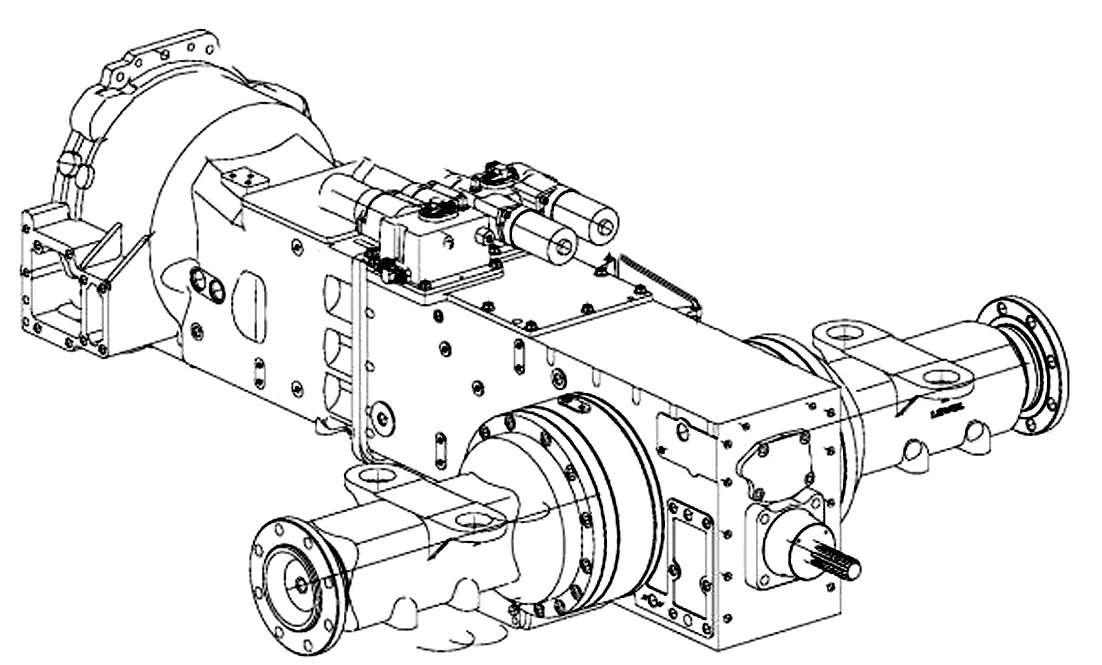
图1 拖拉机变速器三维结构图
以拖拉机变速器拆卸实例,在Win11 系统下使用Matlab2022 开发算法程序,运行环境为Intel ©Core i5@3.4GHZ,RAM 8.00G。 设置算法参数为:种群规模N=200,外部档案个数Q=15,邻域解个数S =9,最大迭代次数M =90,节拍CT =60 s,单位待机碳排放ε0=2 500 g CO2。
通过50 次算法迭代,果蝇算法的平均运行时间为36.25 s,每次运行得到9 个拆解序列的Pareto 解,表2 为果蝇算法求解得到的非劣解集。 若按照拆解方案1 执行拆解作业,则工作站数为4,拆解时间为256 s,拆解费用为73 元,碳排放为51 500 g CO2。 为了更好地反映Pareto 解的空间分布,在三维空间中反应解的分布情况,其中f1、f2和f3分别代表x 轴、y轴和z 轴。 因此,Pareto 解的空间分布如图2 所示。

表2 Pareto 非劣解集

图2 Pareto 解集空间分布
为了说明果蝇算法的有效性与稳定性,选择传统的遗传算法和人工蜂群算法进行对比分析。 遗传算法和人工蜂群算法的计算框架与果蝇算法相近,在工程研究中被广泛用作基准算法,可以作为本研究的对比算法。 为了体现果蝇算法求解的优越性,遗传算法和人工蜂群算法采用相同的编码解码规则以及目标函数,并选用特征指标超体积(HV)、收敛度量(CM)和间距度量(SM)作为对比指标特征,各算法的求解结果如表3 所示。 从表3 中可以看出,果蝇算法得到的非劣解个数最多;对于CM 值,SM值和HV 指标,果蝇算法表现出较好的性能;同时果蝇算法在运行时间上也少于另外两种算法。 因此,果蝇算法对于求解农机拆解模型有效且稳定性好。

表3 算法性能对比
4 结论
本研究针对退役农机产品拆解回收的规划问题进行研究,考虑了拆解完工时间、拆解成本以及拆解碳排放多目标优化问题,建立了多目标拆解规划数学模型。 根据退役农机拆解特点,提出了一种果蝇优化算法用于求解拆解规划模型。 运用拖拉机变速器拆解案例分析,将果蝇算法应用于实例求解,得到9 个Pareto 非劣解。 最后,与遗传算法和人工蜂群算法对比分析,验证了果蝇算法求解的有效性和稳定性。
