基于FLAC3D对某边坡天然及地震工况下稳定性分析

2023-10-09彭志盛中交四航局第二工程有限公司

珠江水运 2023年17期

◎ 彭志盛中交四航局第二工程有限公司

1.前言

当前稳定性分析有定性和定量分析两类方法。极限平衡法，极限分析法等是定量分析方法中比较常见的[1]。无论极限平衡法或是极限分析法具因其模型简单、计算方便，在工程实践中作为首选方法进行广泛应用，但分析边坡破坏发生和发展过程方面却力有不逮[2]；针对此问题，基于强度折减法理论的数值模拟软件FLAC3D通过搜索潜在滑动面及其位置可以有效解决极限平衡法的不足，计算呈现结果更加直观。进行数值模拟计算时，参数的选取至关重要，参数选取准确与否对计算结果影响重大，而当前岩土体，尤其是岩质材料的参数取值时往往进行以下简化：以岩石（岩块）室内试验所得性质代替真实岩体。工程实践中极少遇到未风化岩体，天然环境中的岩体受风化作用产生广泛分布的节理裂隙，影响岩体完整性，并使得真实岩体在物理力学性质上与岩块存在较大差异。

本文以某工程挖方边坡为例，对岩体材料基于更科学的方法进行取值，采用强度折减法进行天然工况及地震工况下分析边坡稳定性。

2.强度折减法

强度折减法中稳定性系数即边坡达到临界状态与初始状态对应的抗剪强度之比。岩体抗剪强度应用过程如下式所示。

式中：

Cd—折减后的粘聚力；φd—折减后的内摩擦角；C—折减前的粘聚力；φ—折减前的内摩擦角；Fd—折减系数。

FLAC3D软件进行迭代计算时，对岩体强度进行不断折减，直至边坡处于不稳定状态时，此时计算不收敛，此时的折减系数即为边坡稳定性系数；另外，抗剪强度进行不断迭代折减的过程，可以用来分析边坡的渐进破坏过程[3]。

3.RMR分类法及其应用

对于岩体抗剪强度参数选取方法，目前常用的有现场试验法、经验公式法等；现场试验能取得最为直接也比较可靠的参数，但费时费力，而室内试验以岩块为研究对象，不能准确反映实际岩体的各项性能。

工程实践中采用经验公式法进行保守估算是比较常见的做法。以Q值法、RMR法和BQ法为基础，通过结合各类强度准则甚至结合诸多文献资料中的现场试验数据来提出各自的经验公式是众多学者努力的方向，也涌现出诸多经验公式，但不同学者思维重点以及自身所处的区域性会导致根据其经验公式所得结果出现很大差异[4]。

许宏发等[4]根据《工程岩体分级标准GB50218-94》表C.0.1绘制[BQ]与各物理力学参数之间的关系曲线，见图1。该方法由于是对规范附表试验数据统计为基础，具有一定的可信度和广泛的适用性。

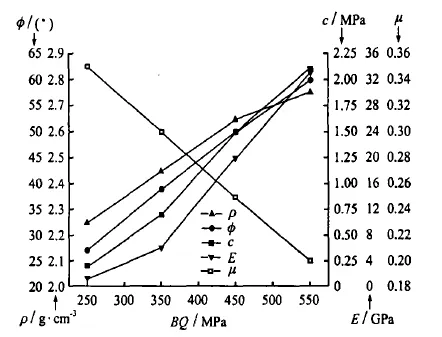
图1 岩体物理力学参数确定图[4]

随后，许宏发等[5]通过非线性拟合分析建立各物理力学参数与[BQ]之间关系的经验公式并按照一定等效原则，提出[BQ]值与RMR值之间的关系方程，如下式所示：

式中：

R M R— 岩体R M R 值；[BQ]—岩体修正BQ值；γ—岩体重度，单位N/m3；

φ—岩体内摩擦角，单位°；c—岩体内摩擦角，单位k P a；E—岩体弹性模量，单位M Pa；μ—岩体泊松比。

4.工程概况

拟研究边坡为位于某地的切方边坡，长约280米，高50米；表层覆盖砂砾石，厚度约为0.2米。边坡后部分布有当地居民房屋。坡体植被不发育。气温分布比较平均，常年无雨，场地地表水不发育。

4.1 地层岩性

主要由中风化板岩及闪长岩组成，板岩与闪长岩互层状产出，但存在两处全风化岩层，厚度在0.8—0.9m之间。在第一、二级坡面有砂层向坡体内延伸，但延伸距离不远。典型地质断面如图2所示。

4.2 地震

位于环太平洋地震带，地震多发，板块运动频繁，地质条件不稳定。场地地震专项研究表明，工程区当地50年超越概率10%的地震加速度为0.542g（相当于重现期475年），规范取值为0.45g，相当于国内最大抗震设防烈度9度，工程设计按照0.542g。

4.3 支护设计方案

坡体设置锚杆长度4或6m，锚杆与水平向夹角调整为1 5°，间距2.0m。锚杆直径18mm，由grade 60（ASTM A615）钢筋制成，钻孔直径50mm，灌注M30水泥浆。

5.边坡稳定性分析

5.1 岩土体物理力学参数选取

本文基于R M R 法进行参数估值，给出该边坡岩土体的力学参数，具体数值见表1和表2。

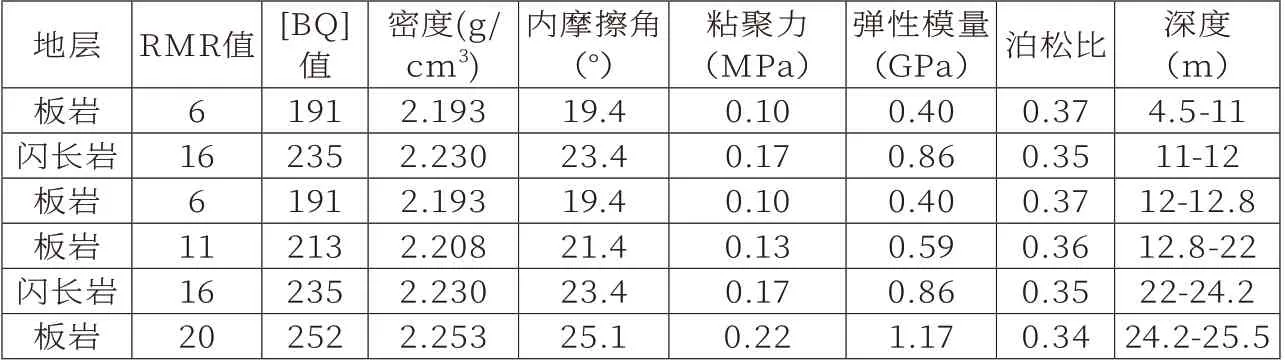
表1 各岩层物理力学参数

表2 ZK01砂层物理力学参数

砂层内摩擦角取值依据如下标贯击数与内摩擦角经验关系：

砂层其余参数参照《工程地质手册》（第五版）表3-1-24，得到参数如表2所示。

表3 锚杆参数表

场地中各岩体所取R M R值均小于2 1，围岩级别划为Ⅴ级（岩质极差），根据《工程岩体分级标准GB50218-2014》表D.0.1对于岩体物理力学参数的推荐值，与表1所取数据进行对比，可以发现，本次计算所用参数值均在规范推荐值的合理范围内。

5.2 数值模型建立及本构模型选取

由于模型的不规则性，现有FLAC3D版本建立模型比较困难，因此本次报告中按照CAD剖面图→迈达斯GTS→FLAC3D顺序建立三维地质模型。模型按照地层分布情况共划分7个组（group），为尽可能减少边界条件影响，计算范围选取：垂直方向取（2～3）倍边坡高度；水平方向取（1.8～3）倍边坡高度。在X、Y方向设置水平约束，在底部即Z=0面设置水平和竖向约束，模型顶部无约束，为自由面[6-7]。模型建立后，为提高计算准确性及效率，网格划分时按照自上而下逐渐加密的原则进行，网格划分后的模型如图3所示。

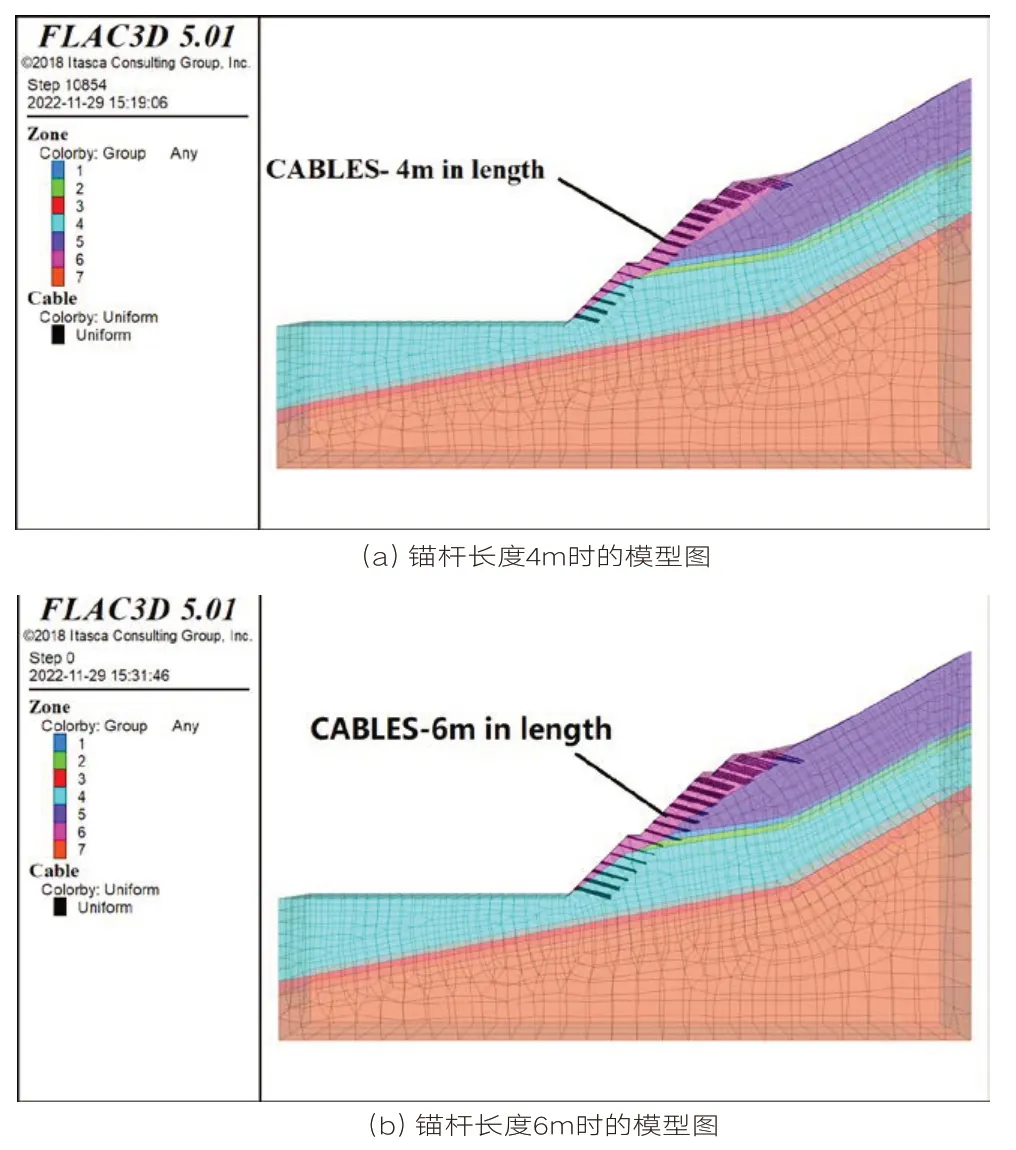
图3 不同锚杆长度时的模型图

本构模型选择方面，以该模型所包含岩土体在力学特性方面符合度高低为标准[8]，即本构模型的选择要以材料的力学特性以及该模型的适用范围为准。对全部岩土体材料采用摩尔－库伦本构进行计算。

5.3 计算结果及分析

5.3.1 天然工况下的稳定性结果

建好模型之后参照表1～表3中各参数进行赋值，并设置边界条件，即可得到基于强度折减法进行计算的各边坡稳定性结果，如图4所示。图中所示Factor of Safety即为边坡稳定性系数值。

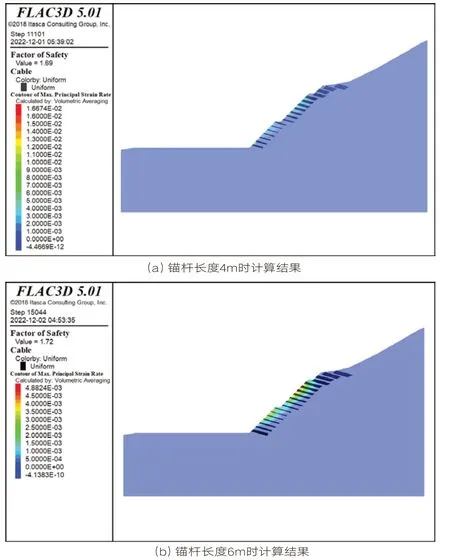
图4 天然工况下不同锚杆长度时的稳定性分析结果

对各模型计算结果进行统计，如表4所示。

表4 天然工况下稳定性计算结果

5.3.2 地震工况下的稳定性结果

我国现行抗震设计规范中，对于安全系数的计算均采用拟静力法。姚令侃等[9]指出，高烈度区域支挡结构破坏率仅为7%，这表明基于拟静力法设计的支挡结构是偏于保守的。拟静力法沿用边坡静力稳定性分析的基本思想，将地震作用等效为一个水平和竖向的单向加速度作用，并施加在潜在不稳定的滑体重心上，加速度的方向取为使边坡失稳的方向。笔者参考《滑坡防治设计规范》[10]中推荐的公式对地震荷载进行处理，计算公式如下：

式中：

Fh i—滑体i 的水平向地震荷载；aw—综合水平地震系数。

式中：

Wi—滑体i的重量；ai—滑体i的动态分布系数一般取值为1～3；Fvi—滑体i的竖向地震荷载；ah—滑体i的竖向地震荷载；ξ—折减系数，取0.25；g—重力加速度。

将建立好的模型赋予相应物理力学参数，并设置边界条件，得到地震工况下基于强度折减法进行计算的边坡稳定性结果，如图5所示。图中所示Factor of Safety即为边坡稳定性系数值。

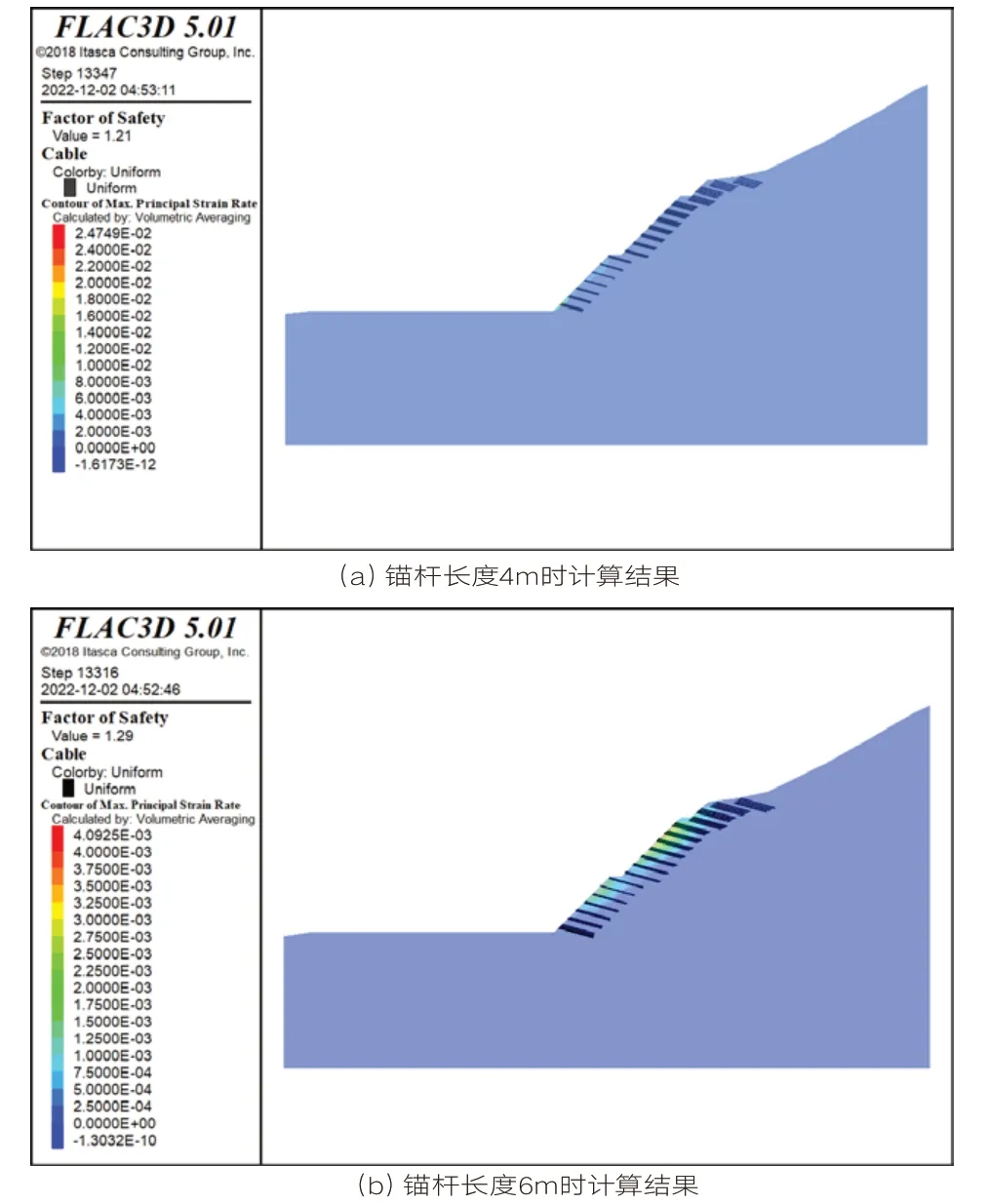
图5 地震工况下不同锚杆长度时的稳定性分析结果

对各模型计算结果进行统计，如表5所示。

表5 地震工况下稳定性计算结果

6.讨论

《建筑边坡工程技术规范》（GB50330-2013）中对边坡稳定性状态划分如表6所示。

表6 边坡稳定性状态划分[11]

对于边坡不同的安全等级状况，只要边坡稳定性系数不小于其需要的安全系数即可判定该边坡处于稳定状态。针对该边坡，按照安全等级为一级考虑，根据《建筑边坡工程技术规范》（GB50330-2013）中表5.3.2，对天然工况和地震工况下分别取1.35和1.15。

采用基于强度折减法对边坡计算结果显示：天然工况下，锚杆长度4m时，稳定性系数为1.69；锚杆长度6m时，稳定性系数为1.72；地震工况下，锚杆长度4m时，稳定性系数为1.21，锚杆长度6m时，稳定性系数为1.29。无论天然工况还是地震工况，稳定性系数均满足规范对安全系数的要求，边坡处于基本稳定状态。

但是笔者注意到，在分析过程中：①各岩体所取R M R值均小于21，围岩级别划为Ⅴ级（岩质极差），岩体相应物理力学参数也以此为基础取值，实际岩体质量应优于Ⅴ级；②砂层内摩擦角取值以表层0-3.5m内的标贯值为基础进行计算，实际上深部砂层性质要优于表层；③由于拟静力法计算特点，采用此方法对边坡进行地震工况下较为保守。综合以上分析可以看出，计算所得稳定性系数应是较为保守的，实际稳定性系数要大于计算结果，说明对于该边坡采用4m或6m锚杆进行支护，该边坡均是基本稳定的，但为留出足够安全余量，建议采用6m锚杆。