地下连续墙技术在港口航道工程中的应用

◎ 刘成斌 江西省路港工程有限公司

地下连续墙结构具有强大的截水、挡土、防渗性能，施工扰动小，整体刚度强，环境影响小，在深基坑支护方面应用广泛。地连墙成槽时，主要以已完工导墙为导向，借助成槽机开挖出深槽单元，再进行钢筋笼吊装及混凝土灌注。在成槽及钢筋笼吊装时，因地面超载及土体应力释放等原因，槽壁失稳的可能性较大，槽壁稳定问题也越来越受到工程界的重视。现行规范及施工中的一些控制性标准对土压力取值、拉杆设计等缺少明确规定，部分施工参数主要依托土工离心模型试验确定，而该试验存在比尺及边界效应，应用受到较大限制。

为此，本文以某港口航道整治工程为例，应用ABAQUS有限元软件构建地下连续墙整体结构模型，展开锚碇桩、地连墙形变特性及拉杆内力变化的模拟分析，为工程地下连续墙施工质量控制提供依据。

1.工程概况

某港口航道为三级航道，整治后护岸底板顶高程应达到-1.0m，如果采取重力式护岸形式，必将增大基坑开挖难度。为将整治施工对航道通航的不利影响降至最低，应在近护岸处采取无需开挖大规模基坑、振动小的地下连续墙结构。工程区为典型的亚热带季风气候，雨量充沛，四季分明，设计最高、最低通航水位分别为3.3m和0.6m。

结合地勘资料，工程区以长江中下游冲积平原地貌为主，从上往下依次为素填土层、淤泥质粉质黏土层、粉质黏土夹粉砂层、粉质黏土层。各地层特性见表1。

表1 工程区地质条件

2.施工方案设计

该航道整治工程护岸结构下部采用地下连续墙形式，上部为混凝土胸墙。钢筋混凝土地连墙按前后2排设计，排距为8.0m，墙身为C25混凝土，墙体厚度为0.6m，顶底高程分别为0.5m和-0.8m；纵向按8.8m间距增设1道横向地连墙，以形成格构，增强结构整体稳定性。在地连墙顶浇筑帽梁和盖板，其上再浇筑C25混凝土胸墙，胸墙顶高程2.5m，顶底宽0.3m和0.5m。

3.有限元分析

结合该港口航道工程实际及锚碇桩-拉杆-地下连续墙结构体系，构建包括锚碇桩、拉杆、地下连续墙、土体等在内的整体有限元模型[1]，见图1。其中，锚碇桩、地下连续墙及土体单元全部为平面4节点等参单元；拉杆则为平面2节点杆单元。在应用平面应变模型展开分析时，厚度按照单根拉杆影响厚度（即1.5m）确定。坐标系中x向与闸室垂直，向右为正向；y向与闸室平行，竖直向上为正向。所构建的有限元模型共包括8784个单元和9071个节点。

图1 二维有限元网格

3.1 材料本构模型

通过线弹性本构模型展开地下连续墙、锚碇桩、井字梁、拉杆等的数值计算。根据《水工混凝土结构设计规范》（SL 191-2018）拟定的材料参数见表2。在展开二维计算的过程中，锚碇桩弹性模量应按照刚度等效原则折减，最终折减为5940MPa。

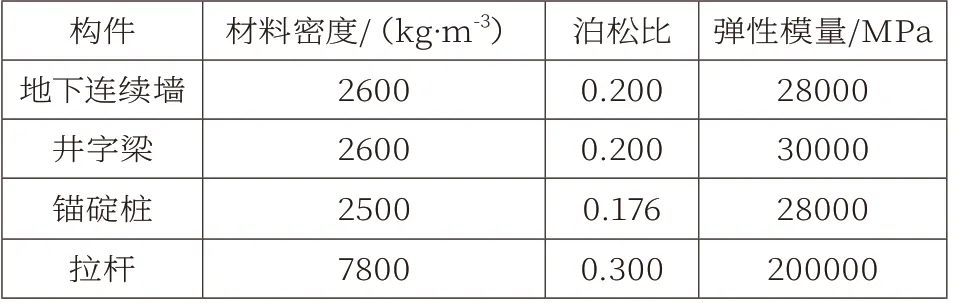
表2 材料参数

土体采用线弹性本构模型时，计算值与实际值存在较大差异，无法满足地下连续墙板桩结构形变规律；在采用Mohr-Coulomb和Drucker-Prager弹塑性本构模型时，因模型中并未将土体与地下连续墙间的非线性接触剔除，故计算结果无法收敛[2]。经过反复测试后，最终选用Duncan-Chang本构模型，以保证地下连续墙板桩结构形变规律契合工程实际，并保证计算结果的收敛性。Duncan-Chang本构模型属于非线性弹塑性模型，其弹性模量与应力状态呈函数关系，能对土体应力应变关系做出较好描述；还能针对卸荷、加荷土体选用不同模量，较好体现土体形变的弹塑性特征[3]。该模型无法反应土体剪缩性和剪胀性，但涉及参数少、参数确定过程简单，故具有较强的应用优势。

3.2 接触本构模型

地下连续墙和土体间采用点面接触形式，本构模型见图2；本构关系[4]可表示如下：

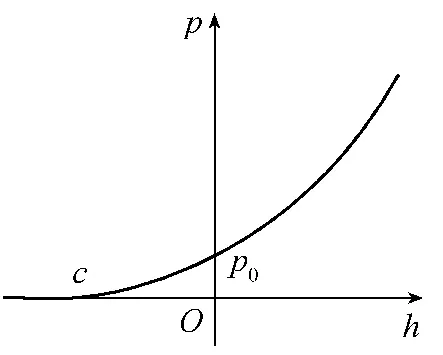
图2 接触本构模型

式中：P为地下连续墙与土体接触点的接触压力；P0为地下连续墙与土体的特征接触力；h为地下连续墙与土体接触面相对位移，嵌入时取正；c为地下连续墙与土体初始接触间距。

在h≤-c的情况下，地下连续墙和土体接触面为张开状态，接触压力为0；而在h＞-c的情况下，接触压力P与相对位移h呈指数关系。为将接触面两侧张开状态下相互作用控制在最低范围，并在接触面闭合时确保地连墙对土体的挤压力学特征能光滑过渡，应控制地下连续墙与土体初始接触间距c，同时增大P0值。在地连墙与土体接触面间嵌入深度足够小时，该模型收敛性较好，精度较高。综合以上分析并结合工程实际，c取0.05mm，P0取1.0MPa。

3.3 计算方案

结合工程实际，将该港口航道地下连续墙板桩结构填筑及开挖划分成21级和5种计算工况，具体见表3。土体开挖及填筑过程均应用ABAQUS软件的Model change功能模拟，闸室井字梁在浇筑前属于土体结构，浇筑后变为钢混结构，浇筑前后材料本构模型不同。考虑到ABAQUS软件不具备改变同一模型中同一结构单元材料本构模型的功能，只能通过其Import功能予以实现，故在分析时必然涉及数据传递。

表3 地下连续墙填筑及开挖工况

3.4 计算结果分析

3.4.1 锚碇桩及地连墙形变

根据模拟结果，在地下连续墙后土体回填及开挖施工期间，锚碇桩整体向闸室侧倾斜，且其顶部位移值最大，待此项施工任务结束后最大位移达到1.79m。进一步分析表明，锚碇桩变位受闸室土体开挖的影响较大，锚碇平台位移从工况2下的0.21cm增至工况3下的1.59cm；桩基位移增至工况3下的0.58cm；待完成闸室井字梁浇筑施工任务后桩基位移降至0.55cm。

此外，在地下连续墙后土体回填及开挖施工期间，地连墙也整体向闸室侧倾斜，最大位移发生在-2.00～0.00m高程之间，待结束填筑和开挖后最大位移达到3.17m。引起地连墙变位的主要原因同样为闸室开挖，地连墙位移从工况2下的0.22cm增至工况3下的2.69cm；墙体根部位移增至工况3下的0.76cm；待完成闸室井字梁浇筑任务后墙体根部位移降至0.64cm。

3.4.2 拉杆内力及影响

根据对不同施工阶段拉杆内力变化曲线（图3）的分析，地下连续墙后土体回填及开挖施工结束后拉杆内力值达到588.74kN；闸室的开挖使拉杆内力从开挖前的34.98kN快速增至开挖后的450.79kN；随后在回填地连墙板桩墙后土体期间，拉杆内力基本趋缓。

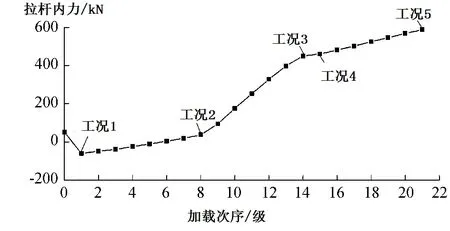
图3 1#拉杆内力变化曲线

与设置拉杆的情况相比，去掉拉杆后，锚碇桩水平位移从1.76cm降至1.32cm；地连墙水平位移则从3.01cm增至13.41cm，对闸室安全稳定极为不利。

3.5 实测值与模拟值的比较

为展开施工期间锚碇桩和地下连续墙形变情况的监测，预先在相应位置埋设了测斜管，并在拉杆上提前安装了应变计。通过对实测值和模拟值的比较看出，锚碇桩、地下连续墙形变模拟结果与实测结果基本吻合，锚碇桩最大水平位移实测值为1.75cm，与模拟值（1.7 9 c m）的误差仅为2.28%；地连墙最大水平位移实测值为2.96cm，与模拟值（3.17cm）的误差为7.09%；最大拉杆内力实测值为525.67kN，与模拟值（588.74kN）的误差为11.99%，均未超出规范允许值，故模拟结果合理可信。

4.施工工艺要点

4.1 挖槽、成槽、泥浆护壁及清底

待将地面整平后修筑导墙，导墙接头和地连墙接头应当错开布置，并在导墙内按1.0m左右的间隔增设上下两道木支撑，避免导墙发生形变和位移。

地连墙成槽所用泥浆必须在使用前展开配比试验，以确定原材料配合比和化学剂掺加量，测定出泥浆各项物理力学性能。新制备出的泥浆必须掺加分散剂或放置24h以上，确保黏土或膨润土充分水化后方可使用。施工期间应密切关注工程区地下水位的变化；成槽期间若出现漏浆，必须通过蛭石、木屑等挤塞填充泄露点。

槽底清淤后淤泥厚度应不超出15cm，待挖槽至设计高度后通过超声波测量槽段断面，一旦误差超出精度，必须修槽。挖槽结束并检查合格后清底。

4.2 钢筋笼吊放

将保护垫板增设在钢筋笼两侧，并按照设计要求设置钢筋笼吊点，配置吊钩和架空钢筋，受力钢筋笼骨架在施工过程中的变形不得超出要求。钢筋笼吊放入槽前，必须再次展开槽段检查，各项指标符合要求后再吊放。

4.3 混凝土浇筑

考虑到该港口航道工程地质条件的特殊性，应在地连墙施工时将混凝土提升一级强度等级展开配合比设计。待完成钢筋笼吊装并摆放到位后，通过导管浇筑混凝土；导管埋入混凝土中的深度应控制在2.0～4.0m，浇筑期间混凝土面升高速度应不低于2.0m/h，最终浇筑面应高出墙顶设计标高0.5m，以确保将涂浆层凿除后顶标高仍符合要求。

施工期间可能因地质条件、操作工艺等原因而引起槽壁坍塌，为此，必须事先根据水文地质及超前地质勘探结果，做好防范与应对。

5.结论

综上所述，对于港口航道整治工程而言，因地质条件复杂，施工现场干扰因素多，施工难度较大。在正式施工前通过有限元分析，对不同施工阶段锚碇桩、地连墙的形变情况及拉杆内力展开模拟，模拟结合与实测结果基本吻合，为施工过程控制提供了依据。工程应用结果表明，地下连续墙施工后结构性能合格，结构连续密实，稳定性好，综合利用价值高，投运后能极大提升港口航道通行质量，护岸墙后还配合设置了自嵌块结构二级生态护岸，具备显著的经济效益和环境效益。