改进鲸鱼优化算法及其在混流U型装配线平衡问题的应用
2023-10-09张凌波周剑扬
张凌波, 周剑扬
(华东理工大学信息科学与工程学院, 上海 200237)
鲸鱼优化算法(whale optimization algorithm,WOA)具有收敛速度快,性能稳定等优势,自从提出以来广泛应用于故障诊断[1]、参数调优[2]、水资源配置[3]和模型优化[4]。但同其他的智能优化算法一样,存在收敛精度较低,易于陷入局部最优等问题,已有许多学者对其进行了研究和改进。黄元春等[5]提出一种伪反向学习和高斯-柯西混合变异策略的改进鲸鱼算法,改善了算法的收敛速度和精度;吴坤等[6]将灰狼优化算法中的等级制度和微分进化算法中的贪婪策略引入鲸鱼优化算法,提升了算法的全局搜索能力;Jiang等[7]将差分算法和鲸鱼优化算法结合,并引入云自适应惯性权重,有效平衡全局和局部搜索。上述改进虽然改善了WOA的性能,但是在寻优精度和算法稳定性方面还存在不足,仍有改进空间。
装配线是由一些物料搬运设备连接起来连续生产线,由多个工位组成,每个工位完成整个装配过程的几个环节。由于任务分配的不合理,装配线各工位的负载并不均衡,就会出现“瓶颈工序”,造成资源的浪费和生产效率低下。装配是生产过程的重要环节之一,据调查,装配占用总生产时间的50%和总生产成本的20%。
装配线平衡问题(assembly line balancing problem,ALBP)是指根据装配线的已知信息,合理地将各工序分配至各个工作站,优化装配线某些指标的一系列复杂问题。常见的装配线平衡问题主要可以分为3类,即第1类装配线平衡问题(ALBP-Ⅰ)、第2类装配线平衡问题(ALBP-Ⅱ)、E类装配线平衡问题[8](ALBP-E)。ALBP-Ⅰ是已知装配线的节拍时间,最小化装配线的工作站数量;ALBP-Ⅱ是已知装配线的工作站数量,最小化装配线的节拍时间;ALBP-E是最小化工作站数量和节拍时间,提高装配线效率。装配线根据类型,可以分为直型线、U型线和并行线;根据生产产品的类型,又可分为单模、多模和混模。随着市场变化和精益生产的发展,越来越多的企业采用灵活性更好的混流U型线代替传统的单模直型线,这使得混流U型线的平衡问题(mixed model U-shaped assembly line balancing problem,MMUALBP)成为近几年的研究重点;彭运芳等[9]针对第2类混流U型装配线的平衡问题,构建了其混合整数规划模型,并提出了一种改进的遗传算法,采用3种工序分配方法,并通过实验验证了算法的有效性;刘佳楠等[10]针对直型线和U型线的混流装配线平衡问题,提出多目标的平衡方法,并采用改进的遗传算法进行优化;原丕业等[11]的研究兼顾工作站的平均和瞬时负荷,建立了混流U型装配线的多目标数学模型,并设计了一种自适应遗传算法求解;Aufy等[12]针对混流直型和U型线的装配线平衡问题,设计了一种工人-任务分配的启发式模型,并通过实例验证其模型的有效性;Zhang等[13]以最小化混流U型装配线的能源消耗和生产效率为目标建立了多目标模型,并设计了一种改进的多目标蜻蜓优化算法求解;Zheng等[14]基于任务选择因子的编码方式,提出一种混合交叉熵算法,用于解决混流U型线的平衡问题。如何合理地分配工序和更精准的求解,是混流U型装配线目前需要解决的问题。
针对鲸鱼优化算法在实际应用中存在寻优能力不足、求解效果不稳定和易于陷入局部最优等问题,现提出一种改进的鲸鱼优化算法(improve whale optimization algorithm,IWOA),并将其应用到求解混流U型装配线平衡问题。在WOA的基础上,现引入均匀设计方法进行初始种群的生成,提高初始种群的质量;融合NEWUOA算法,增强鲸鱼优化算法的局部搜索能力;提出一种新的越界处理方法,降低算法陷入局部最优的可能;引入非线性收敛因子和自适应权重,平衡算法的局部和全局搜索,增加算法的搜索精细度。通过7个基准测试函数,验证IWOA在寻优效果和求解稳定性方面的优越性。针对混流U型装配线平衡问题,以装配线节拍时间为优化目标,设计带阈值的工序分配方法。最后通过21个混流装配线标准算例,进一步验证本文提出的IWOA的有效性。
1 标准的鲸鱼优化算法
WOA是Mirjalili等[15]通过对座头鲸特有的气泡网狩猎方式进行研究和模拟,建立数学模型,而后提出的一种智能优化算法。该算法包括包围猎物、气泡网攻击和搜索猎物3个阶段。
1.1 包围猎物
WOA通过假定当前的最优个体所处的位置即为猎物或者最接近猎物的位置,以此吸引其他个体向着最优个体移动,完成对猎物的包围,其过程可以描述为
D1=|CX*(t)-X(t)|
(1)
X(t+1)=X*(t)-AD1
(2)
式中:D1为中间变量;t为当前的迭代次数;X*为最佳鲸鱼个体的位置;X为当前鲸鱼个体的位置;A和C为系数,定义为
A=2ar-a
(3)
C=2r
(4)
式中:r为[0,1]的随机数;随着迭代次数的增加,收敛因子a线性地从2减至0。
1.2 气泡网攻击
鲸鱼个体根据自身和猎物之间的距离,通过一种对数螺旋方程更新位置,其过程可以描述为
X(t+1)=D2eblcos(2πl)+X*(t)
(5)
式(5)中:D2=|X*(t)-X(t)|为当前鲸鱼个体和猎物之间的距离;e为自然常数;b为螺旋对数方程常数;l为[-1,1]的随机数。
为了更好地模拟座头鲸的这种独特捕食行为,WOA设置了一个概率阈值,用于在包围和螺旋更新两种行为之间进行选择,通常情况下,两种行为的概率都为50%,其数学模型为
(6)
式(6)中:p1为[0,1]的随机数。
1.3 搜索猎物
WOA会根据系数A的值来决定是靠近最优个体进行包围猎物或螺旋更新,还是远离最优个体进行随机搜索。当|A|>1时,WOA将随机选择参考个体Xrand,执行全局搜索,而不再是以最优个体为参考。过程可以描述为
D3=|CXrand(t)-X(t)|
(7)
X(t+1)=Xrand(t)-AD3
(8)
2 改进的鲸鱼优化算法
WOA具有实现简单、可调参数少和收敛速度快等优点,广泛应用于工程问题优化,但在实际应用中发现,WOA存在寻优精度不足、易于陷入局部最优等缺点。针对上述问题,在WOA的种群初始化、局部搜索、越界修正和收敛因子方面提出了几点改进措施,具体如下。
2.1 基于均匀设计的种群初始化策略
一般的智能优化算法使用随机方式进行初始种群的生成,这样的初始种群只具有一定的随机性,而不能保证有较好均匀性。均匀试验设计,简称均匀设计,是由Fang等[16]提出的一种试验设计方法,用于将试验点均匀的散布在试验区域内,尽可能地减少试验次数。以往采用均匀设计的智能优化算法[17-18]大多使用好格子点法进行均匀设计表的生成,但是好格子点法要求试验次数n和因子个数s满足式(9)的限制:
(9)
式(9)中:φ(⋅)为欧拉函数。
这要求优化算法的种群数量要足够大,但对于群智能优化算法,过大的种群数量意味着算法运行时间的增多。切割法[19]的思想是从一个较大的均匀设计中切割出一个符合条件的偏差最小的均匀设计作为近似均匀设计。相较于好格子点法,切割法只要求较大的均匀设计的试验次数p或p+1为素数,可用于算法求解高维复杂问题时初始种群的生成。IWOA采用基于切割法的均匀设计种群初始化方法,并使用方幂好格子法作为切割法的初始设计,混合偏差作为均匀性度量,混合偏差的公式为
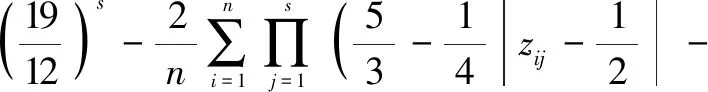
(10)
式中:zij为第i个点的第j维坐标。
2.2 基于NEWUOA的局部搜索算子
NEWUOA是一种无导数优化方法[20],用于求解求导困难、无约束的黑箱问题。NEWUOA是一种基于信赖域的确定性优化算法,采用二次逼近的方式,不需要计算目标优化函数的导数。因此,NEWUOA和智能优化算法具有很好的契合度。NEWUOA的流程可以描述如下。
步骤1选择初始插值点xi,计算F(xi)中的最优值,设定最优值对应的xi为xopt。构建初始的二次模型Qinit,设定参数ρ=ρbeg,Δ=ρbeg。
步骤2计算‖d‖≤Δ条件下Q(xopt+d)的近似最小值,其中d为信赖域子问题的近似解。如果‖d‖<Δ,则将参数CRVMIN的值设置为二次模型Q的最小曲率值。
步骤3如果‖d‖>ρ/2,则计算F(xopt+d),设定参数RATIO为[F(xopt)-F(xopt+d)]/[Q(xopt)-Q(xopt+d)],并在参数Δ≥ρ条件下调整ρ的值。将参数MOVE设置为0或者下次迭代过程中要舍去的插值点的索引。如果‖d‖<ρ/2,则跳至步骤11。
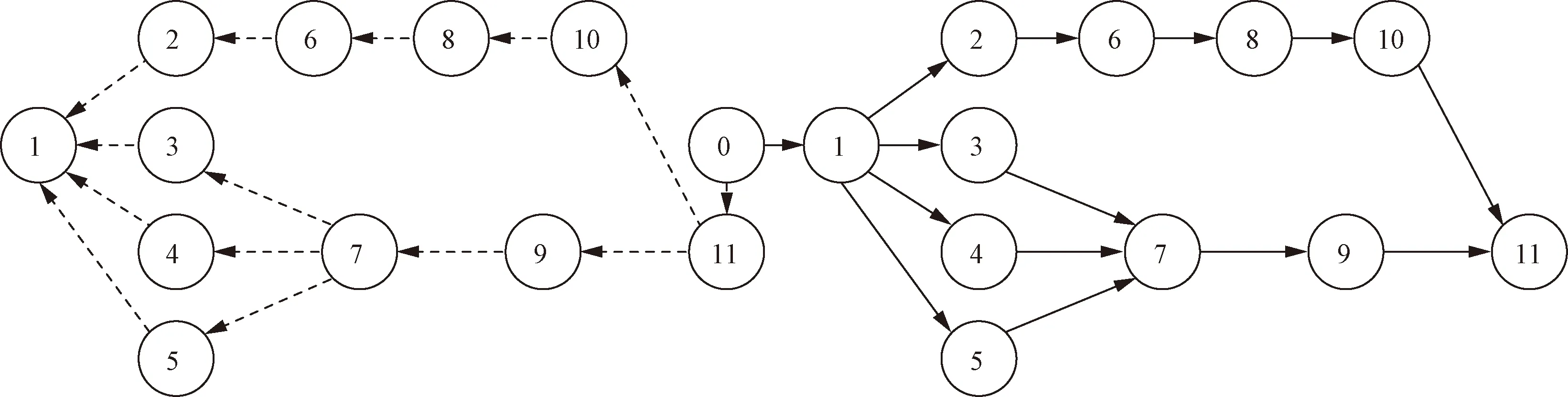
步骤4如果MOVE>0,则更新二次模型Q,将xMOVE替换为xopt+d。如果F(xopt+d) 步骤5如果RATIO≥0.1,则跳转至步骤2。 步骤6将xMOVE设置为当前迭代中使得距离参数DIST=‖xMOVE-xopt‖最大的插值点。 步骤7如果DIST≥2Δ,跳至步骤10。 步骤8如果参数d、Δ、RATIO满足‖d‖≤ρ,Δ≤ρ,RATIO≤0,转至步骤9;反之,转至步骤2。 步骤9如果ρ=ρend,转至步骤13;反之,转至步骤10。 步骤10将参数ρ在满足约束ρ≥ρend下缩小10倍,并将Δ设置为max{ρold/2,ρnew},跳至步骤2。 步骤11使用参数CRVMIN测试‖d‖的最近3个值和F-Q是否足够小,如果是,则转至步骤9,反之跳至步骤12。 步骤12设置参数ρ为原来的1/10且不低于其下界值,RATIO=-1,转至步骤6。 步骤13如果||d||<ρ/2,则计算F(xopt+d)后,算法终止;否则,直接终止算法。 NEWUOA具有优越的局部搜索能力,初始点的选取影响着优化结果,而WOA的种群更新依赖于引导个体,优秀的引导个体可以更好地引导种群的搜索方向。通过融合NEWUOA,由WOA提供全局最优个体作为NEWUOA的初始点,同时WOA借助NEWUOA进行更好的局部搜索,优化引导个体,从而提高自身的寻优能力。在算法初始运行时,对种群中最优个体执行一次NEWUOA,如果种群最优值发生变化,则继续对种群最优个体执行NEWUOA,反之,则停止执行NEWUOA,直到累计30次迭代,种群最优值都没有发生变化,则继续启用NEWUOA,重复上述过程。 大部分智能优化算法在处理越界问题上一般会舍弃越界个体或直接将越界个体修正至边界,这样可能会导致该个体频繁越界,致使算法陷入局部最优。采用一种基于环形区间和随机波动的越界修正策略,公式为 (11) 式(11)中:mod(n1,n2)为修正的按模运算,假设n1=pnn2+re,pn为正整数,re为余数,当re>0时, mod(n1,n2)=re;当re=0时,mod(n1,n2)=n2;p2和rand(0,1)为[0,1]的随机数;lb和ub分别为算法搜索区域的下界和上界;Xi(t)为个体第i维的坐标。 A是控制WOA进行全局搜索和局部搜索的关键参数,其变化受到a的影响。根据文献[5]中的研究,a不同变化趋势对算法的全局搜索和局部搜索存在一定程度的影响。为均衡算法的全局和局部搜索,引入的非线性收敛因子a的计算公式为 (12) 式(12)中:Max_iter为最大迭代次数。 经式(12)改进后,a在算法迭代过程中的变化趋势为先缓后急,增加了算法全局搜索所占用的迭代次数比例,增强了算法的全局搜索能力。此外,为进一步增加算法的搜索精细度,设计了一种自适用权重ω,随着迭代进程的推进,ω可以使得种群在最优个体附近进行更加精细的搜索,其计算公式为 (13) X(t+1)=ωX*(t)-AD1 (14) X(t+1)=D2eblcos(2πl)+ωX*(t) (15) 本文提出的IWOA伪代码如下。 注:T为迭代次数;Tmax为最大迭代次数。 图1给出了IWOA更加直观的流程图。 为了验证IWOA的性能,选择7个基准测试函数,如表1所示,与几种工程上常用的智能优化算法以及其他的改进鲸鱼算法比较,包括遗传算法(genetic algorithm, GA)、WOA、PWOA[5]、GWOA[6]、BWOA[21]、NWOA[22]和RWOA[23]。测试函数中,F1~F3为多模态函数,F4为固定维度的多模态函数,F5~F7为单模态函数。测试指标包括最优值、最差值、均值、标准差、和平均运行时间。测试软件为MATLAB2021b,测试环境为11th Gen Intel(R) Core(TM) i7-11800H @ 2.30 GHz,16 GB RAM。 表1 基准测试函数 参与测试的算法参数设置如下:遗传算法[24]的精英保留个数设置为2,交叉率0.7,变异率0.1;WOA和IWOA中参数b都遵循WOA,文献[15]设置为1,其余改进鲸鱼优化算法的参数设置均参考其原文献。所有算法的种群大小设置为30,迭代次数上限为500次,算法终止条件为|f(x)-fmin|≤10-5或达到最大迭代次数。为避免随机性,对每种算法独立运行1 000次。测试结果如表2所示。 表2 算法测试结果 由表2可知,在寻优精度方面,相较于其他算法,IWOA在测试函数F1~F2和F4~F7上求得的结果最优,仅在F3上略差于其他算法,这得益于IWOA采用NEWUOA算法作为其局部搜索算子的一部分,增强了算法的搜索能力,并通过引入了自适应参数,增加算法的搜索精细度;在算法求解稳定性方面,IWOA在7个测试函数中的最差值指标均是最小的,此外,在F1~F2和F4~F7中的均值和标准差指标也是最小的,即更接近最优值的均值和更小的标准差,仅在F3中的均值和标准差指标略差于PWOA,这表明在所有参与测试的算法中,IWOA在求解稳定性方面具有一定的优越性。 在平均运行时间方面,IWOA在F1、F3、F4和F6上取得了最短的平均运行时间,而在其余3个测试函数中要差于其他算法。图2给出了所有算法在迭代500次的过程中最优值的均值随迭代次数的变化曲线。由图2可知,IWOA在F2、F5和F7中的收敛曲线所表现出的特性为在迭代前期快速收敛,在中后期略慢于PWOA和GWOA,但最终仍可收敛至最优值;在F1、F4和F6中,IWOA在收敛精度方面表现出显著优势,并且可以在较小的迭代次数内快速收敛至最优值或其附近,收敛曲线位于所有算法的下方;在F3中,IWOA同样在前期有着最快的收敛速度,但其收敛精度要低于PWOA。 图2 收敛曲线 综合上述结果,相较于其他算法,IWOA具有更高求解精度和更好的求解稳定性,虽然所提出的改进措施对运行时间存在一定的负面影响,但仍可在前期加快算法的收敛。 第2类混流U型装配线平衡问题就是已知工作站的数量,在混合模型和U型装配线的情况下,最小化装配线的节拍时间。相较于一般的单模直线型装配线平衡问题,混流U型装配线平衡问题的复杂性更高,主要体现在:①单模的装配线只生产单一品种的产品,其各个工序的装配时间相对固定,而混流的装配线生产多种工艺相似,品种不同的产品,不同产品相同工序的装配时间存在差异;②直线型装配线的工序分配只能按照工序的顺序,例如从前往后或从后往前进行,而U型线的工序分配更为灵活,可以同时从装配线的前后进行工序的分配。为了降低混流装配线平衡问题的复杂度,一般采取的方式是根据各产品主生产计划(master production schedule,MPS),构建综合工序优先级图[25],将“混流”转换为“单模”问题,如图3所示,模型A、B、C的MPS为1∶1∶1。本文所建立的数学模型基于以下假设:①每中产品的工序所需的装配时间是固定值,不受其他因素的影响;②所有模型的优先级图都可以构成综合优先级图;③不同产品的相同工序须分配到同一个工作站;④所有产品的工序优先级相同。 圈中数字表示工序序号;圈上数字表示工序时间 针对第2类混流U型装配线的平衡问题,优化目标定义为最小化节拍时间Ct,如式(16)所示。 minCt (16) 模型同时需要满足相关约束: (17) (18) (19) (20) (21) (22) 式中:M为模型数量;dm为模型m的需求;D为模型总需求;K为工作站数量;N为工序数量;tjm为模型m的工序j所需装配时间;Tj为工序j的加权时间;P为工序优先级集合;xjk和yjk为决策变量,分别为分配顺序从前向后和从后向前时,工序j是否分配给工作站k,是则为1,反之为0。 式(17)为装配线上生产产品的总需求;式(18)为综合优先级图中各工序根据MPS计算得出加权装配时间;式(19)表示每一道工序都被分配至一个工作站;式(20)表示每个工作站的总装配时间不得超过节拍时间;式(21)和式(22)表示向后和向前的工序分配需要满足工序的优先级约束。 采用优先级权重的编码方式,初始对每道工序赋予[0,1]的随机数,作为该工序的优先级权重,以Jackson问题为例,其编码如图4所示。 图4 Jackson优先级权重编码 解码就是将种群个体的编码信息解释成工序分配信息,为更好地进行工序分配,本文提出一种带阈值的工序分配方法。根据影子约束关系[26],如图5所示,从前后两个方向进行分配,具体步骤如下。 图5 影子约束关系图 步骤2根据P,同时向前向后搜索无约束的工序,将无紧前工序的工序(P列和为0)放入P1中,无紧后工序的工序(P行和为0)放入P2中。 步骤3分别P1和P2中选择优先级权重最大的工序a和b并比较其权重大小,如果a的权重大于等于b,转至步骤4,否则转至步骤5。 步骤4如果满足|TSk+TSa-Ctbest|≤|Ctbest-TSk|且|TSk+TSa-Ctbest|≤B,则将工序a分配至工作站k,TSk=TSk+TSa,将P中工序a所在的行置为0并转至步骤2;否则尝试分配工序b,如果满足|TSk+TSb-Ctbest|≤|Ctbest-TSk|且|TSk+TSb-Ctbest|≤B,则将工序b分配至工作站k,TSk=TSk+TSb,将P中工序b所在的列置为0并转至步骤2,否则转至步骤6。 步骤5如果满足|TSk+TSb-Ctbest|≤|Ctbest-TSk|且|TSk+TSb-Ctbest|≤B,则将工序b分配至工作站k,TSk=TSk+TSb,将P中工序b所在的列置为0并转至步骤2;否则尝试分配工序a,如果满足|TSk+TSa-Ctbest|≤|Ctbest-TSk|且|TSk+TSa-Ctbest|≤B,则将工序a分配至工作站k,TSk=TSk+TSa,将P中工序a所在的行置为0并转至步骤2,否则转至步骤6。 步骤6如果k=K-1,将剩余工序分配至工作站K,输出分配结果,结束工序分配程序,否则k=k+1,转至步骤2。 图6给出了解码的流程图。 为了验证IWOA在求解装配线平衡问题上的性能,采用网站(https://assembly-line-balancing.de/)[27]中的混流数据集作为测试算例,具体数据信息如表3所示,选择与第3节中相同的算法作为对比算法。测试指标为节拍时间和对应的平衡率,平衡率RB的计算公式为 表3 混流装配线测试算例 (23) 4.4.1 参数设置 针对Thom、Kim、Arcus三组问题,设定算法的迭代次数为500。为避免随机性,对每种算法独立运行10次,取最优值作为最终结果,并对表中结果的最优值进行加粗处理,其余参数设置和测试环境与第3节中保持一致。 4.4.2 结果和分析 表4给出了8种算法的对比结果。根据表4可知,在简单问题Thom1~Thom3上,所有算法均可以求得最佳的生产节拍;在6个中等规模的问题Kim1~Kim6中,IWOA在所有的算例中都能够求得更小的节拍时间;在12个大规模的问题Arcus1~Arcus12中,IWOA在11个算例中求得了最小的节拍时间,这说明IWOA具有更好的寻优能力。Arcus9~Arcus12因为存在单个工序装配时间超过工作站平均装配时间的情况,所以无法达到100%的平衡率。 图7给出了所有算法在部分用例中的收敛曲线图。在简单算例Thom1中,所有算法都可以在前几次迭代快速收敛至最优值,而在中等算例Kim1和大规模算例Arcus3,IWOA虽然在前期的收敛速度要落后于其他算法,但仍可收敛至更优的值。上述的实验结果验证了IWOA的有效性,能够在复杂问题上求得更好的解。 图7 部分算例的收敛曲线 以最小节拍时间作为优化目标,建立了第2类混流U型装配线平衡问题的模型,并提出了一种改进的鲸鱼优化算法IWOA进行模型的求解。算法采用均匀设计作为初始种群的生成策略,提高初始种群的均匀性;采用NEWUOA算法作为IWOA的局部搜索算子,强化算法的局部搜索性能;在处理越界点时采用一种基于环形区间和随机波动的修正策略,降低算法陷入局部最优的可能;最后引入了非线性收敛因子和自适应权重系数,平衡算法的全局和局部搜索,增强算法的搜索精细度。针对第2类混流U型装配线平衡问题,IWOA的采用优先级权重的编码方式,并采用一种带阈值的解码方案,尽可能地得到更好的工序分配方案。通过7个基准函数测试和21个装配线标准算例测试表明IWOA在一般问题上的求解精度和稳定性高于对比算法,同时在复杂问题的优化效果也要优于对比算法,验证了算法改进的有效性,为工程中解决混流U型装配线的平衡问题提供了可行的解决方案。2.3 基于环形区间和随机波动越界修正策略
2.4 非线性收敛因子和自适应权重系数
2.5 IWOA步骤

2.6 算法复杂度分析

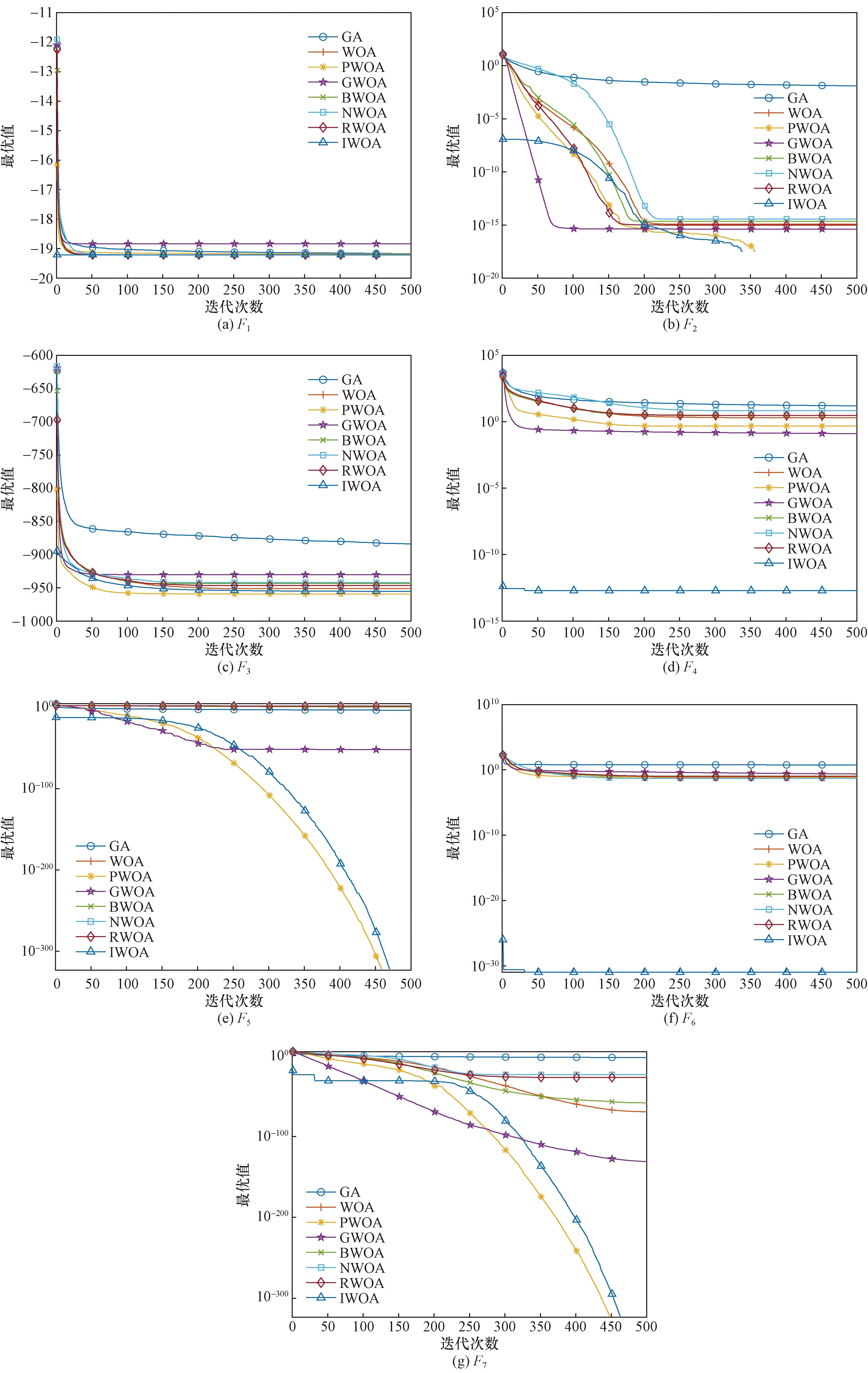
3 仿真实验结果与分析


4 基于改进鲸鱼优化算法的混流U型装配线平衡优化
4.1 问题描述

4.2 数学模型
4.3 编码与解码


4.4 算例测试结果与分析


5 结论
