区域乡村住宅耐久性指标全局敏感性分析方法

李垂帅, 唐贞云*, 高晓明, 王威

(1.北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124; 2.中国建筑标准设计研究院, 北京 100048)

近年来,国家对乡村住宅建设和发展的重视程度不断增加。2018年,中共中央、国务院印发《乡村振兴战略规划(2018—2022)》[1],明确提出要建设生态宜居的美丽乡村。中国乡村住宅长期处于村民自建,建造模式混乱,既有乡村住宅在住宅设计和施工质量上存在诸多安全性问题。在乡村振兴和生态宜居乡村建设的背景下,安全性能的提升,耐久性能的增强,实现住宅长寿化成为乡村住宅的未来发展方向,同时,乡村住宅新建和改造的需求也在不断提升。在乡村住宅新建和改造过程中,如何对乡村住宅的性能进行评价和敏感性分析,得到乡村住宅性能的敏感因素,确定住宅的改造方向成为重要问题。

当前中国已有学者对乡村住宅的性能和评价方法进行了相关研究,金虹等[2]、金玲等[3]、宋平等[4]和郑文亨等[5]对乡村住宅的热环境进行了研究,总结了中国严寒地区、粤东地区、重庆地区和桂北山区民居的室温和热舒适性规律。杜运兴等[6]、包相相等[7]、胡云香等[8]、田易卓等[9]和高源等[10]对乡村住宅的评价方法进行了相关研究,在安全性、建筑节能、基础设施适用性、混凝土碳化和低碳化改造等方面提出了相应的评价方法。张华等[11]、仇春华等[12]和张欣伟等[13]对乡村住宅的评价体系进行了研究,建立了室外通风、住宅设计和耐久性能的指标体系。胡恬等[14]和冯涛等[15]对乡村住宅的墙体和地面面层等建筑材料进行了相关研究,进一步推动了乡村住宅向生态宜居住宅的转变进程。

上述研究多集中于乡村住宅的热环境、建筑材料和性能评价方法,针对乡村住宅性能的敏感性分析方法的研究较少。李垂帅等[16]对乡村住宅耐久性能的敏感性分析方法进行了研究,提出了一种适用于单体乡村住宅和区域乡村住宅的敏感性分析方法,然而,该方法在用于区域乡村住宅的性能评价和敏感性分析时,未考虑敏感因素之间的相互影响,且需要对乡村住宅进行大范围实地调研。实地调研时间周期长,资金成本高,并且自新冠肺炎疫情暴发以来,对乡村住宅进行大范围跨地区实地调研的难度增加。在保证乡村住宅耐久性能的敏感性分析准确度的前提下,如何减小实地调研的范围,同时,获得足够用于敏感性分析和规律总结的乡村住宅样本成为困扰乡村住宅研究的难题。

鉴于此,现提出将扩展傅里叶灵敏度检验法(extended fourier amplitude sensitivity test, EFAST)和最小二乘支持向量机算法(least squares support vector machines, LSSVM)用于区域乡村住宅耐久性能的敏感性分析,提出乡村住宅耐久性能的敏感性分析方法,分析区域乡村住宅耐久性能的薄弱项。同时,在对乡村住宅进行性能分析时,对乡村住宅样本数量进行合理扩增,从而缩小乡村住宅实地调研的范围,节省调研时间,降低调研成本,减小疫情等不确定因素对调研活动的影响,以提高调研效率。

1 基于可拓学-EFAST的敏感性分析

为考虑乡村住宅耐久性敏感因素之间的影响,提高耐久指标敏感性分析的准确性,现将可拓学和EFAST方法相结合,用于乡村住宅耐久指标的敏感性分析。EFAST法在敏感性分析过程中考虑了敏感因素之间的相互影响,准确度更高,但EFAST法对样本数量的要求更多。可拓学的计算对样本数量要求低,可以初步筛选出耐久指标的敏感因素,但计算流程复杂,准确度较低。因此,将两者结合可以在降低样本量,减小计算代价的同时,提高模型计算的准确度。

下面从模型建立和数据分析两方面阐述本文区域乡村住宅耐久指标的全局敏感性分析方法的具体实现,技术路线图如图1所示。

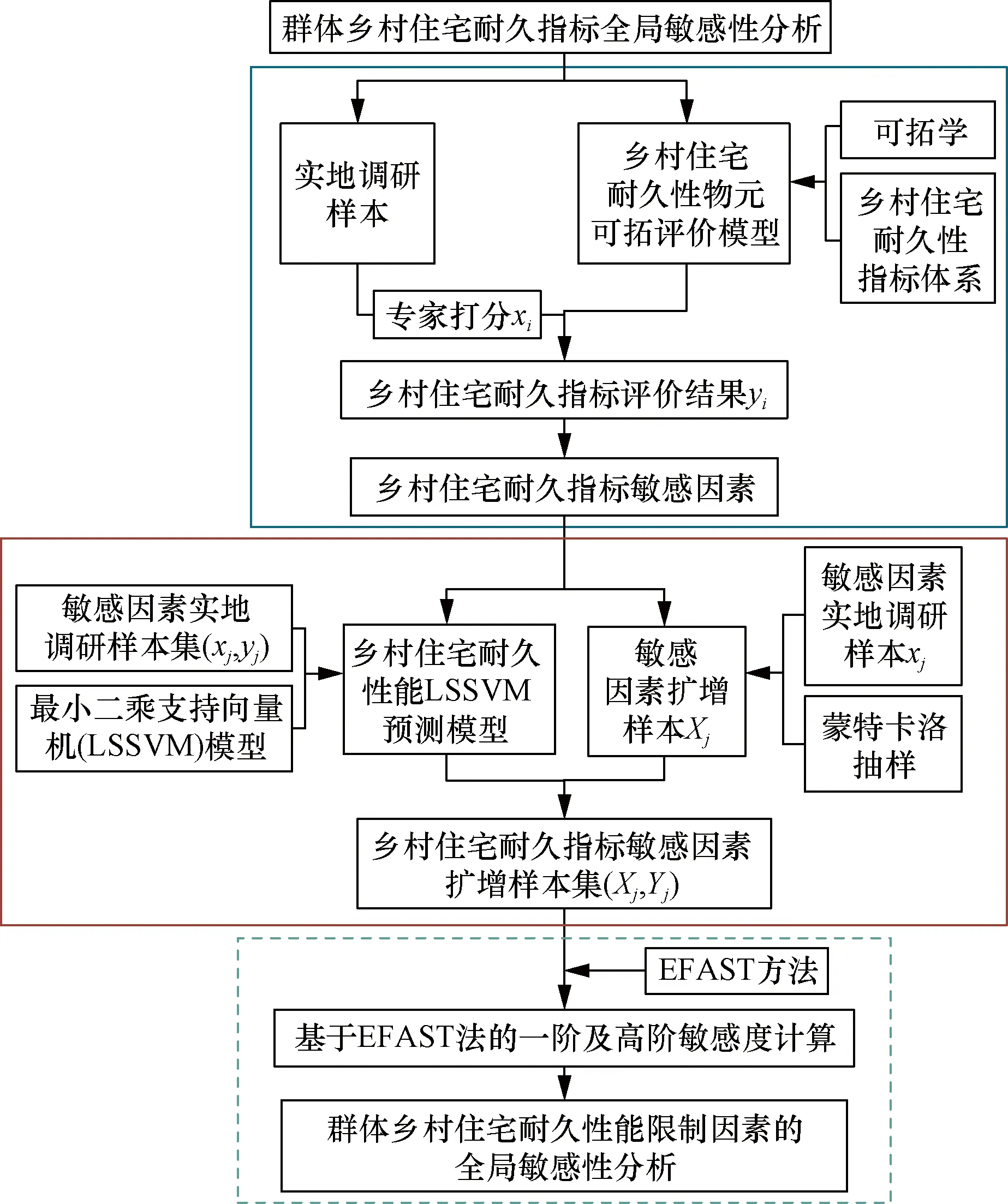
图1 区域乡村住宅耐久性的全局敏感性分析模型

首先,选用合适的乡村住宅耐久性能指标体系,依据指标体系的评价标准对乡村住宅实地调研样本进行专家打分;结合选用的指标体系和可拓学建立乡村住宅耐久性物元可拓评价模型;将专家打分的数据xi输入物元可拓评价模型,得到乡村住宅耐久性评价结果yi;对乡村住宅耐久性评价结果yi进行分析对比[16],得到乡村住宅耐久性能敏感因素,实现耐久指标的筛选。

其次,为获得足够数量的乡村住宅样本用于EFAST敏感性分析,对筛选得出的敏感因素实地调研样本xj进行蒙特卡洛抽样,实现敏感因素样本数量的扩增,得到敏感因素扩增样本Xj;将敏感因素实地调研样本集(xj,yj)用于最小二乘支持向量机(LSSVM)模型的训练和预测,得到符合乡村住宅耐久性能预测精度的LSSVM模型,实现乡村住宅耐久性的预测功能;将敏感因素扩增样本Xj输入乡村住宅耐久性能LSSVM预测模型,得到与扩增样本Xj相对应的耐久性能评价结果Yj。综上,本步骤通过蒙特卡洛抽样(Monte Carlo)和乡村住宅耐久性能LSSVM预测模型实现乡村住宅耐久性敏感因素样本集(Xj,Yj)数量的扩增。

最后,通过EFAST方法对扩增后的乡村住宅耐久指标敏感因素样本集(Xj,Yj)进行敏感性分析,得到敏感因素的一阶敏感度和总阶敏感度,实现区域乡村住宅耐久指标的全局敏感性分析。

2 乡村住宅耐久指标

为提高区域乡村住宅耐久性能的敏感性分析准确度,将EFAST方法引入乡村住宅的敏感性分析,但EFAST法要求样本数量至少为敏感因素数量的65倍以上。为保证敏感性分析的准确度,同时,减小用于EFAST法敏感性分析的乡村住宅样本,通过可拓学的计算对耐久指标的敏感因素进行初步筛选。可拓学基本原理[17]如下。

针对乡村住宅评价的不同性能,选择相应的指标体系。依据乡村住宅指标体系和指标实测值xi建立物元矩阵R,即

(1)

式(1)中:R为实测值物元矩阵;P为可拓评价与敏感性分析的对象;c1～cn依次为可拓评价指标体系的n项指标;x1～xn依次为指标体系的n项指标的实测值。

计算关联函数Kj(xk),即

(2)

式(2)中:

(3)

式中:j为评价等级;Kj(xk)为关联函数,表示待评价事物的指标ck关于评价类别j的归属度;|xjk|为指标ck的区间长度,即bjk-ajk;ρ(xk,xjk)为点xk与区间xjk的距;ρ(xk,xpk)为点xk与区间xpk的距。

计算关联度Kj(P),即

(4)

式中:Kj(P)为在考虑指标权重下,待评价事物各指标ck关于类别j的关联度的组合值;λk为各个指标的权重。

依据最大隶属度原则,确定评价等级,如式(5)所示,评定P为j0等级。

Kj0(P)=maxKj(P),j=1,2,…,m

(5)

计算级别变量特征值y,即

(6)

式(6)中:

(7)

级别变量特征值y的取值范围为(1,m),通过耐久指标级别变量特征值y和评价等级j0的横向、纵向对比得到乡村住宅耐久指标的敏感因素,完成耐久指标的初步筛选。

为了解中国乡村住宅的耐久性能现状,分析当前乡村住宅耐久性能的限制因素,选取江苏、浙江和安徽等20个省份的105个典型村庄进行了实地调研,调研村庄的分布情况如图2所示,调研过程发现,乡村住宅具有长期处于村民自建,缺乏专业的布局与结构设计,建造前未进行地质勘探,抗震防火措施布置不当,建筑材料质量差,设备管线安置不合理,建成后缺乏定期维护更新等特点。因此,规划布局、防灾设计、建筑材料、施工质量、维护性能是决定乡村住宅耐久性能和使用年限的重要因素。

括号中数值为乡村住宅数量

张欣伟等[13]参考中外现行住宅评价标准,结合中国乡村住宅的特点,建立了包含功能耐久性、物理耐久性、安全耐久性和耐久性维护的乡村住宅耐久性能指标体系,指标体系如表1所示,评价等级划分为B级、1A级、2A级、3A级。因此,级别变量特征值y取值范围为(1,4),y=1.0对应评价等级为B级,y=4.0对应评价等级为3A级。依据该指标体系的评价标准对实地调研的105个村庄进行专家打分,得到指标实测值x,通过可拓学计算得到乡村住宅的耐久性评价结果y(图3),乡村住宅耐久性能(目标层)的级别变量特征值y为3.0,依据目标层和二级指标评价结果的纵向对比,户型设计A2、设备管线A3、结构工程B1、连接设计C2、维护便捷性D2的评价结果低于目标层评价结果。

表1 选用的乡村住宅耐久性指标体系

图3 乡村住宅耐久性能二级指标评价结果

因此,该五项二级指标为乡村住宅耐久性能的敏感因素。

3 乡村住宅样本量扩增

为将可拓学计算筛选得到的敏感指标进行EFAST敏感性分析,需要大量乡村住宅样本,而对乡村住宅进行大范围实地调研费时费力,且受疫情影响进展困难。鉴于此,本文研究建立最小二乘支持向量机算法(LSSVM)代理模型,通过105个乡村住宅实地调研样本对LSSVM模型进行训练,实现乡村住宅耐久性的预测功能。符合预测精度要求的LSSVM模型,可以结合对敏感因素样本x蒙特卡洛抽样得到的扩增样本X实现乡村住宅敏感因素样本集数量的扩增。

3.1 LSSVM代理模型的构建

最小二乘向量机(LSSVM)是在支持向量机的基础上提出的一种变形算法。LSSVM利用二范数对目标函数的优化公式进行变形,并将支持向量机中的不等式约束条件转换为等式约束条件,从而将二次规划问题转换为线性方程组问题,简化计算流程,节省计算时间。LSSVM在具备了SVM泛化能力强、全局最优等特点的基础上,训练时间短,结果更具确定性[18]。

LSSVM建模的基本原理如下。

给定样本{(xj,yj),j=1,2,…,m},xj、yj分别为乡村住宅耐久性能敏感因素的输入值和输出值,m为样本数量。在高维特征空间中建立式(8)所示的线性回归函数。

y=wTφ(x)+b

(8)

式(8)中:w为权值向量;φ(x)为非线性映射函数;b为偏差量。

依据结构风险最小化原理,目标函数minJ(w,ξ)为

(9)

式(9)的约束条件为

yj=wTφ(xj)+b+ξj

(10)

式中:ξ为训练集的误差变量;ξj为第j个样本的误差;c>0,为正规化参数,用于减小模型复杂度,提高函数的计算速度。

最小化函数的Langrange求解方程为

L(w,ξ,α,b)=(w,ξ)-

(11)

式(11)中:αj为Langrange乘子。

KKT条件为优化问题的关键,依据KKT条件得

(12)

消去w和ξj,得到式(13)的方程组,即

(13)

LSSVM在计算过程中可依据分析对象的特点选用不同的核函数,由于径向核基函数(radial basis function, RBF)训练速度快、计算精度高[19],适用于乡村住宅耐久指标的训练与学习,本文研究选用RBF函数作为LSSVM的核函数。RBF核函数表达式为

(14)

式(14)中:σ为核函数的宽度参数。

在引入RBF核函数后,得到LSSVM回归函数为

(15)

为验证准确性,进行单位根检验,对训练结果进行误差有效度计算[20]。

(16)

式中:M为LSSVM模型有效度;n为测试样本数;y(xj)为第j个样本的真实值;y′ (xj)为第j个样本的测试值。

为实现乡村住宅耐久性能的预测功能,建立乡村住宅样本扩增的基础,减小调研时间和费用成本,需要建立LSSVM代理模型。将实地调研的105个村庄分为训练组和测试组,训练组包含80个村庄,用于LSSVM代理模型的训练和学习;另外25个村庄用于检验LSSVM代理模型的预测精度。LSSVM代理模型的学习、训练和预测均在MATLAB中实现。测试组的预测结果如图4所示,由图4可知,LSSVM模型的预测结果精准,仅有少量误差,为进一步计算LSSVM模型的精确度,通过式(16)计算模型误差有效度,计算结果为有效度M=0.99,预测结果与真实结果十分接近,符合乡村住宅耐久性能预测模型精度要求。

图4 LSSVM模型预测值与真实值对比图

3.2 蒙特卡洛抽样

对可拓学计算筛选得到的耐久指标敏感因素进行数据分析,得到敏感因素实地调研样本的数学分布规律,如正态分布、均匀分布和指数分布等类型。依据敏感因素的分布类型进行蒙特卡洛抽样(Monte Carlo),实现敏感因素(LSSVM模型输入值xj)的扩增,将扩增后的敏感因素样本Xj输入LSSVM模型,得到扩增样本的乡村住宅耐久性能(LSSVM模型输出值Yj)。扩增的敏感因素样本(Xj)和乡村住宅耐久性能(Yj)满足样本的数量要求和精度要求,可用于EFAST敏感性分析。

将可拓学计算得到五项乡村住宅耐久性能二级指标敏感因素(户型设计A2、设备管线A3、结构工程B1、连接设计C2、维护便捷性D2)按照正态分布进行蒙特卡洛抽样,抽样数量为965,为敏感因素的193倍,将蒙特卡洛抽样后的敏感因素样本值Xj输入LSSVM模型,得到乡村住宅的耐久性能Yj,实现乡村住宅敏感因素样本数量的扩增。

4 乡村住宅耐久指标全局敏感度分析

扩展傅里叶灵敏度检验法(EFAST)[21]是在傅里叶灵敏度检验法(FAST)和Sobol法的基础上改进的一种基于方差分析的全局敏感性分析方法。乡村住宅结构类型复杂多样,建筑质量参差不齐,难以进行定性定量评价。而EFAST方法基于大量的参数取样,具有应用范围广,计算精度高,可进行一阶和高阶的敏感度计算,且计算结果不受模型形式影响的优点[22],因此,EFAST方法适用于乡村住宅耐久指标的敏感性分析。其算法原理如下。

EFAST方法中输出变量Y和输入变量X之间的关系表达式为

Y=f(X1,X2,…,Xm)

(17)

式(17)中:X为输入变量,即蒙特卡洛扩增后的乡村住宅耐久性能敏感因素样本;Y为输出变量,即LSSVM模型输出的乡村住宅耐久性能。

通过傅里叶变换将式(17)转换为式(18),即

(18)

式(18)中:

(19)

式中:uj为Xj的振荡频率;βj为Xj的随机初相位,取值范围为[0, 2π];s为标量变量,取值范围为[-π, π];p为傅里叶变换参数;Ap和Bp为傅里叶系数。

参数Xj变化引起的模型输出方差Vj为

(20)

模型总方差为

(21)

将模型总方差进行分解:

(22)

式中:Vj,q和V1,2,…,m为参数间相互作用的方差。

归一化处理后,Xj的一阶敏感度Sj和总阶敏感度STj为

(23)

式中:Sj为Xj的一阶敏感度,表示Xj对模型总方差V的直接贡献率;STj为Xj的总阶敏感度,表示Xj及Xj与其他参数的相互作用对模型总方差V的贡献率;V-j为不包含Xj的其他参数方差之和。

为提高乡村住宅耐久性能敏感性分析的准确度,选用EFAST法进行敏感性分析。将上文中敏感因素扩增样本Xj和LSSVM模型输出的敏感因素扩增样本的耐久性能Yj用于EFAST敏感性分析,分析过程借助SIMLAB敏感性分析软件实现。EFAST敏感性分析结果如图5所示,乡村住宅耐久指标总阶敏感性从强到弱依次为结构工程B1>设备管线A3>连接设计C2>维护便捷性D2>户型设计A2;一阶敏感性从强到弱依次为结构工程B1>连接设计C2>维护便捷性D2>户型设计A2>设备管线A3。

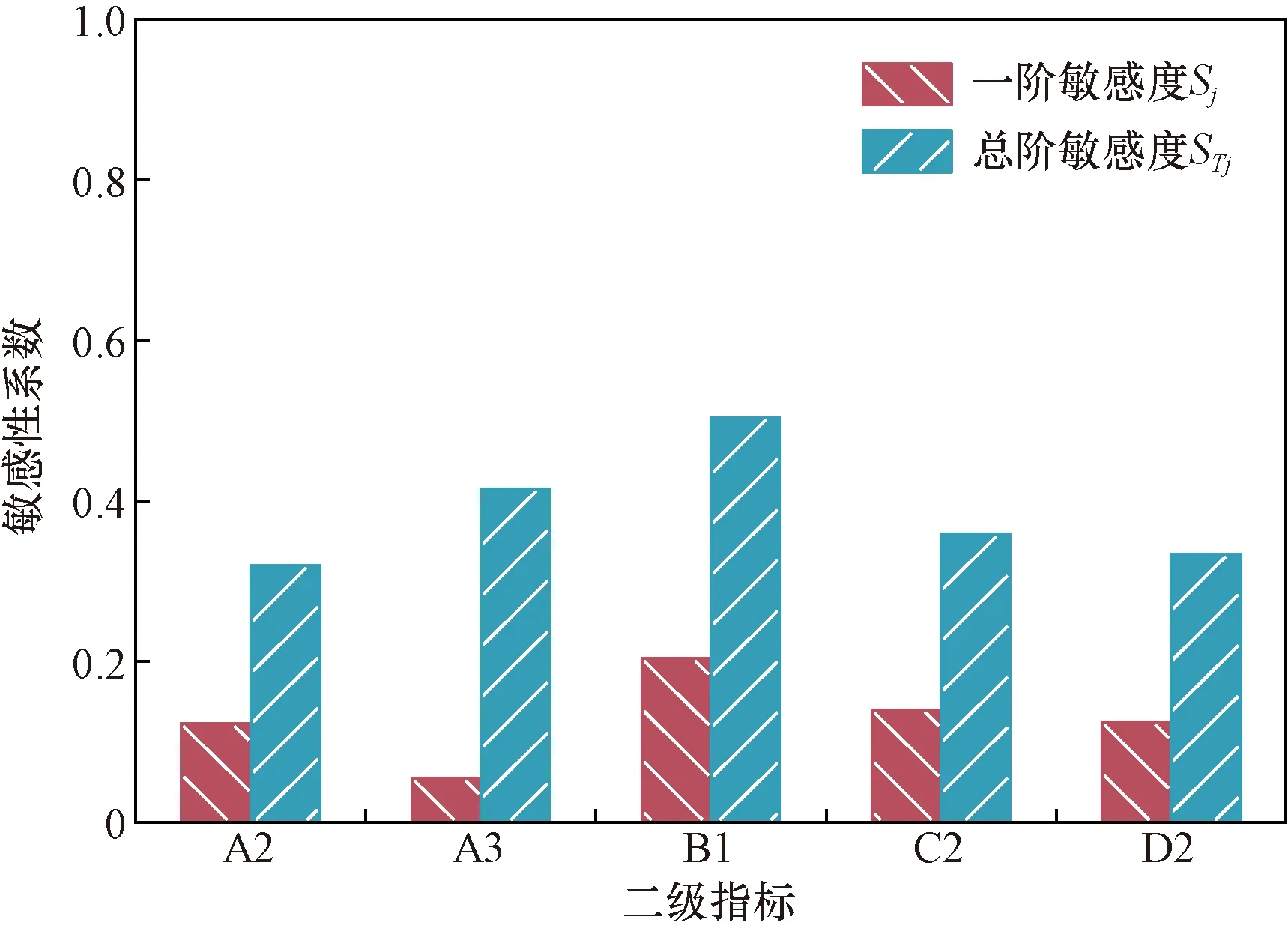
图5 乡村住宅耐久指标敏感性系数

为反映乡村住宅耐久性能的总阶敏感度和一阶敏感度的变动幅度,按照式(24)对敏感因素的敏感度变动比值U进行计算,计算结果如图6所示,设备管线A3受耐久指标间相互影响的作用最大,户型设计A2、结构工程B1、连接设计C2、维护便捷性D2受耐久指标间相互影响的作用较为接近。

图6 乡村住宅耐久指标敏感度变动比值

敏感度变动比值为

(24)

依据上述分析结果,中国既有乡村住宅结构类型以砖混结构为主,受材料选择、施工方法等因素,住宅的结构质量得不到保证,结构安全是影响乡村住宅耐久性能的关键因素。电气和给排水管线的布置欠佳,墙柱、墙梁等连接节点处理不当,住宅部品不便于更换维修,住宅空间体系不合理是限制既有乡村住宅耐久性能的主要因素。同时,电气和给排水管线的布置合理性易受住宅的结构可靠性和部品更新维护便捷性等因素的影响。未来乡村住宅在新建或加固改造过程中应着重对上述问题进行处理。

5 结论

针对区域乡村住宅耐久指标的全局敏感性分析方法进行研究,并应用于区域乡村住宅实例,给出了我国乡村住宅耐久性能的敏感因素和敏感性系数,得出如下结论。

(1)针对区域乡村住宅耐久性问题,结合乡村住宅自身特点,本文研究提出基于可拓学和扩展傅里叶幅度敏感性检验法(EFAST)对乡村住宅进行耐久指标敏感性分析,可拓学可初步筛选出乡村住宅耐久指标的敏感因素,降低EFAST分析的计算代价;EFAST方法可考虑耐久指标之间的相互影响,提高区域乡村住宅耐久性能敏感性分析的准确度。基于该方法可以得到区域乡村住宅耐久性能限制因素的敏感性强弱,为乡村住宅的改造和发展提供了科学依据。

(2)针对乡村住宅大范围实地调研时间周期长、成本高等问题,提出了将LSSVM模型和蒙特卡洛抽样应用于乡村住宅,该方法可以依据少量调研样本实现样本数量的扩增,且该方法精确度高,有效度为0.99。

(3)依据20个省份105个村庄的实地调研情况,结合最小二乘支持向量机模型和蒙特卡洛抽样,扩增出965个乡村住宅样本。通过可拓学-EFAST敏感性分析方法,分析得出,结构安全是影响乡村住宅耐久性能的关键因素;管线布置欠佳,连接节点处理不当,住宅部品更换不便,空间体系不合理是限制乡村住宅耐久性能的主要因素;管线的布置合理性受其他指标参数耦合作用的影响最大。