圆柱斜切体涡激振动压电俘能器的输出特性研究

2023-10-09王航王军雷田海港

科学技术与工程 2023年26期

王航, 王军雷, 田海港*

(1.郑州大学机械与动力工程学院, 郑州 450001; 2.河南省交通科学技术研究院有限公司, 郑州 450001)

随着低功耗的便携式设备和微型无线传感器等微机电系统的应用日益增加,以及能源日益短缺,持续供能问题矛盾突显。传统以化学电池和电子等储能源进行供能,但存在环境污染和需定期更换等问题。以储能源供能的弊端尤为明显,特别在一些偏远更换储能源困难的特殊场合,如偏远山区、原始森林、高楼和桥梁等。结合国家为实现“碳中和”而大力推广的新能源技术,如何为微机电系统持续稳定的自供能成为目前研究的热点之一[1-4]。近些年利用振动俘能技术俘获周围环境振动能并转化为有用的电能,为微机电系统持续稳定的自供能已经成为新能源技术之一,受到了中外学者的广泛关注。利用流致振动收集能量可以在较低的流速下获得较大的电能,能够较好地解决流体速度慢、能量收集难的问题[5-8]。

近年来相关学者对流致振动能量收集做了大量的研究。王军雷等[9-11]提出了一种基于流机电多物理场耦合下的涡激振动能量收集模型。研究了外界载荷对三相耦合圆柱绕流涡激振动能量转换的影响,并且使用矩阵法分析了外界载荷对涡激振动能量转换系统阻尼和固有频率的影响,使用准稳态近似理论推导获得机电耦合系统电压输出的准稳态解析式。研究了完全湍流剪切层下雷诺数对涡激振动动态响应的影响。Wu等[12]研究了不同压电片的长度、不同安装位置对涡激振动压电能量采集的影响。丁林等[13]采用风洞实验,研究了钝体质量、形状以及压电片长度对风致振动能量转换特性的影响。吕振等[14]利用风洞实验研究了低质量比圆柱对涡激振动最大位移响应分支转换特性。Zhou等[15]提出了一种新型的双串联圆柱涡激振动能量采集系统,由两个相同的悬臂式压电涡激振动能量俘能器组成,分别安装在风洞中与来流方向平行的一个平面上,采用格子-玻尔兹曼方法对圆柱涡激振动的振动强度和圆柱周围压力分布进行了数值计算,研究了空间距离对系统能量收集性能的影响。杨敬东等[16]根据压电理论和尾流振子模型建立了二维涡激振动的压电能量收集数学模型,对圆柱加双压电臂的能量收集装置进行计算分析。张敏等[17]采用xFlow与OpenModelica建立了流-机-电耦合计算模型,求解了涡激振动与高斯定律联立方程,通过对涡激振动压电能量收集的数值分析,得到不同电阻下的电压及功率输出。孙洪源等[18]从响应幅值、受力分析方面分析了涡激振动的响应特性。白泉等[19]提出了一种基于汽车减振器的磁力耦合压电振动俘能器,建立了磁-机-电耦合模型并进行了实验,得到增加随机振动信号的幅值能够提升俘获的电压。杨菁等[20]修正了变截面悬臂梁压电俘能器总参数的模型,对相对运动传递函数引入了修正系数,对幅值进行了修正,并对总参数模型得到进一步应用和推广。凌乙峰等[21]研究了并联的双稳态非线性悬臂梁压电俘能器的动力学和俘能特性,得到能够提高俘能效率,拓宽了工作频带宽度。文晟等[22]研究了由金属及压电片组成的复合型压电俘能器的动力学及力电转换特性,分析了压电俘能器的几何参数、不同金属材料对力电转换特性的影响。

目前,利用涡激振动进行能量收集尚存在许多关键问题亟待解决,其中如何通过改变流致振动能量采集器的空气动力学响应来提高能量收集效率具有重要的研究意义。现设计一种斜切角度α分别为30°、45°、60°的圆柱斜切体涡激振动压电俘能器,采用风洞实验对该能量收集装置进行测试和分析,并探究其是否能够提升能量收集效率。

1 物理模型

涡激振动是一种典型的自激振动,结构的非流线型会导致其在流体的作用下产生周期性的旋涡脱落,从而使结构受到与流向垂直的周期性气动力,进而激发结构的横向运动[23]。因此,钝体的结构外形会对涡激振动压电俘能器的振动响应和输出电压产生重要影响[24]。研究了一种斜切角度α分别为30°、45°、60°的圆柱斜切体涡激振动机理。如图1 (a)所示,风垂直于斜切体中轴线的方向流过,在其后方会形成周期性的旋涡脱落,脱落频率达到系统固有频率时,斜切体会产生振动。

图1 圆柱斜切不同角度涡激振动机理示意图

由于悬臂梁和斜切体是固定的,所以位移变化只产生在y轴方向,因此系统可以简化为M-C-K单自由度系统[25]。如图1 (b)所示,悬臂梁等效为弹簧振子。因此该系统的控制方程及机电耦合方程[26]可以表示为

(1)

(2)

表1 压电俘能器系统参数

通过求解机电耦合方程的线性解,获得外接电路对该系统的负反馈效应,从而消除电压项,使得流机电耦合弹簧-振子方程降维,机电耦合方程组的线性形式[27]为

(3)

(4)

(5)

式(5)中:ζ为结构阻尼比。

式(5)可以表示为矩阵形式:

(6)

Z可表示为

Z=[Z1,Z2,Z3]T

(7)

系数矩阵C(R)Z可以表示为

(8)

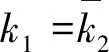
涡激振动系统的振动振幅可以表示为正弦波形式[28],即

y(t)=yvarsin(ω1+φ)

(9)

式(9)中:y为振动振幅;yvar为振幅时变最大值;ω1为机电耦合固有频率;φ为相位角。将式(9)与式(2)进行联立求解,此时的机电耦合输出电压形式[6]为

(10)

由P(t)=V(t)2/R,可以得到机电耦合输出功率P(t)的表达式为

(11)

2 参数测定

制作的实验装置如图2所示,将实验装置放到长度为4 m、直径为0.4 m的圆形风洞中,使用导线与线性电阻负载相连。实验中用到的压电片尺寸为长3.5 cm、宽1 cm、厚0.03 cm,置于铝制悬臂梁顶端,悬臂梁的尺寸为长20 cm、宽2.5 cm,斜切体振动产生的简谐波可以由示波器(ISDS220B)采集。

图2 实验装置

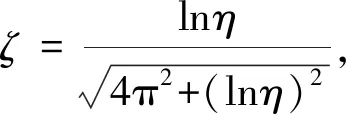
图3 自由衰减实验

3 实验分析

本节分析了在最优负载下,采用不同斜切角的圆柱斜切体涡激振动压电俘能器的输出电压和输出功率随风速的变化规律。

图4为风速分别是2.509、2.646 m/s时,涡激振动压电俘能器输出功率随负载电阻增大的变化情况。两个风速下输出功率均随着负载电阻的增大,先增大后减小,输出功率的最大值均出现在电阻为0.5 MΩ时,所以本次实验最优负载为0.5 MΩ。

图4 风速分别为2.509、2.646m/s时输出功率随电阻的变化曲线

图5为最优负载(0.5 MΩ)下,圆柱斜切角度α分别为30°、45°、60°和光滑圆柱涡激振动压电俘能器的输出电压随风速的变化曲线。当风速在1.413～1.961 m/s时,输出电压均随着风速的增大而增大,且在相同的风速下,输出电压随着斜切角度α的增大而增大,光滑圆柱的输出电压大于斜切角α为60°斜切体的输出电压。风速在2.098～3.194 m/s时,输出电压随着风速的增大先增大后减小,在相同风速下,斜切角度α越小,输出电压越大。在风速为2.509 m/s,光滑圆柱的输出电压最大值为3.022 V。斜切角度α为60°、45°、30°达到最大输出电压对应风速分别为2.783、2.921、3.057 m/s,输出电压最大值分别为3.338、3.708、4.274 V,意味着输出电压最大值向右偏移。压电俘能器的输出电压最大值随着斜切角α的减小而增大;斜切角α为30°的圆柱压电俘能器的输出电压最大值较45°、60°和光滑圆柱分别增加15%、28%和41%。

图5 光滑圆柱及斜切角α为30°、45°、60°圆柱的输出电压随风速的变化曲线

图6为最优负载(0.5 MΩ)下,圆柱斜切角度α分别为30°、45°、60°和光滑圆柱涡激振动压电俘能器(bare cylinder)的输出功率随风速的变化曲线。从图6中可以看出:风速在1.413～1.961 m/s时,输出功率均随着风速的增大而增大,且在相同的风速下,输出功率随着斜切角度α的增大而增大,光滑圆柱的输出功率大于斜切角α为60°钝体的输出功率。风速在2.098～3.194 m/s时,输出功率随着风速的增大先增大后减小,在相同风速下,斜切角度α越小,输出功率越大。当风速为2.509 m/s,光滑圆柱输出功率最大值为0.018 mW;斜切角度α为60°、45°和30°达到输出大功率最大值为0.022、0.027、0.037 mW,对应的风速分别为2.783、2.921、3.057 m/s;涡激振动压电俘能器的输出功率最大值随着斜切角α的减小而增大;斜切角α为30°的圆柱涡激振动压电俘能器的输出功率最大值较45°、60°和光滑圆柱分别增加37%、68%和106%。因此,设计的压电俘能器可放置于沿海、高山、高楼、桥梁等自然界风场中,为低功耗的无线传感器等微机电系统提供一种可持续、有效、绿色的供能方式。