基于ICEEMD-ICA准则进行数据处理的基坑变形组合预测研究
2023-10-08马琳
马 琳
(杨凌职业技术学院建筑工程分院,陕西咸阳 712100)
0 引言
近年来我国加大了对地下空间的开发利用,随之产生了数量较多的基坑工程,在带来巨大经济效益的同时,也引发了不少安全事故(侯凯,2017;齐宏伟等,2018;韩庆华等,2018;赵永,2020;鞠兴华等,2021),使得基坑施工过程的变形控制显得格外重要(刘思敏等,2019;任彦华等,2020;曹浪等,2020;李鉴博等,2020;李常茂和祝和意,2021;李兴盛,2021),因此,开展基坑变形预测研究具有重要的实用价值。一般情况下,在变形预测中,组合预测相较单项预测具有更优的预测精度及稳定性,如王飞(2019,2021)通过组合预测实现了基坑高精度预测,其研究虽取得了一定成果,但其未考虑变形数据的分解处理,忽视了变形数据中误差信息的影响(郭健等,2020),因此,仍可进一步开展基坑变形组合预测。在基坑变形预测中,胡雨菡等(2020)、曹恩华等(2018)验证了相关向量机在基坑变形预测中具有较优的适用性;钟国强等(2019)也验证了广义神经网络在基坑变形预测中的适用性,因此,考虑到相关向量机和广义神经网络具有较优的预测效果,可将两者作为基坑组合预测的基础模型。综合上述,在本文组合预测模型的构建过程中,先开展基坑变形数据的分解处理,然后利用相关向量机和广义神经网络构建组合预测模型,以实现基坑变形预测。通过本文研究,旨在为基坑变形预测提供一种新的思路,并期望变形预测结果可为安全施工提供一定的理论指导。
1 基本原理
在引言分析基础上,将论文分析流程总结为:(1)利用ICEEMD-ICA 准则(Improved Complete Ensemble Empirical Mode Decomposition -Independent Component Analysis,ICEEMD-ICA)对基坑变形数据进行分解处理,即将其分解为趋势项和随机项。
(2)以蛙跳算法(Shuffled Frog Leaping Algorithm,SFLA)、相关向量机(Relevance Vector Machine,RVM)和广义神经网络(General Regression Neural Network,GRNN)为基础,构建基坑变形组合预测模型。
(3)利用传统GM(1,1)模型、支持向量机(Support Vector Machine,SVM)和BP 神经网络对基坑变形数据进行单项传统预测,并将其预测结果与本文模型预测结果对比,以佐证本文组合预测思路的有效性。
结合上述流程,将涉及方法的基本理论详述如下。
1.1 数据分解准则的构建
在基坑变形监测过程中,施工机械、仪器误差及人为因素等都会一定程度上影响变形监测值的真实性,使得监测数据会含有一定的随机信息,因此,可将基坑变形实测数据yt表示为:
式中:qt为趋势项,属基坑真实变形信息;st为随机项,属基坑随机变形信息。
由于随机项具较强的非线性特征,会一定程度上影响变形预测精度,所以,有必要开展基坑数据的分解处理(马还援等,2016;秦鹏飞,2017;孙九春等,2019;苗兰弟等,2021;牛全福等,2022)。
经验模态分解(Empirical Mode Decomposition,EMD)是一种自适应信号处理方法,在变形数据的分解处理中已得到广泛应用,适用性较强,因此,以其为基础构建基坑变形数据的分解准则。
但是,在EMD模型的分解过程中,易出现端点效应、模态混叠等现象,此会影响分解效果,许承权等(2021)则采用引入白噪声等方法,构建了CEEMD模型(Complete Ensemble EMD,CEEMD),有效避免了模态混叠问题,并提高了计算效率和精度;由于CEEMD模型又存在冗余模态问题,许承权等(2021)则进一步对其进行改进处理,构建出ICEEMD 模型(Improved CEEMD,ICEEMD),且此模型的实现流程如下:
(1)通过EMD 模型对原始信号进行1 次分解,并得到第一个余项r1:
式中:<>为整体平均符号;x1为第1 阶模态的原始信号;M()为均布均值的算子符号。
(2)对第1阶的模态IMF1进行计算,即:
式中:x为原始信号。
(3)类比,再对第k阶余项及第k阶模态进行计算,即:
式中:rk-1为第k-1 个余项;xk为第k阶模态的原始信号。
(4)通过上述步骤,可得到所有模态。
同时,为充分保证分解效果,再在ICEEMD 模型分解上,引入独立分量分析(Independent Component Analysis,ICA),以解决分解幅值的不确定性问题。考虑到许承权等(2021)已详述ICA 的基本原理,本文不再赘述。
再进一步将ICEEMD-ICA分解准则详述如下:
(1)先通过ICEEMD 模型对基坑变形数据yt进行有效分解,并计算yt与各IMF 分量间的相关系数,且当k-1 阶处具有相关系数的极小值时,可认定其以前的IMF分量为噪声分量。
将k-1 阶前的IMF 分量进行重构,以得到虚拟噪声noise:
(2)一般来说,实际噪声和虚拟噪声越接近,说明分离效果越准确,且考虑到ICEEMD 模型分解后的高频信号中还可能会含有一定的有效成分,因此,提出对noise信号进行二次分解,以获得更为准确的noise2信号。
(3)将noise2和yt信号输入至ICA 的多维观测通道中,通过FastICA 算法再进行信噪分离,以获得更为有效的信息分解数据。
基于ICEEMD-ICA 准则,已将基坑变形数据分解为趋势项和随机项,但其分解质量仍需进一步评价。结合陈竹安等(2020)的研究成果,提出利用信噪比和均方根误差进行分解效果评价,前者代表原始信号和噪声间的有效功率关系,其值越大越好;后者主要是评价趋势项与真实值间的差异程度,其值越小越好。
1.2 组合预测模型的构建
由于已将基坑变形数据分解为了趋势项和随机项,此节再构建对应的组合预测模型(王兴科等,2017;王雪妮等,2017;余少平等,2017;王更峰,2019;奚家米等,2019)。
1.2.1 趋势项预测模型
考虑到RVM 是于21 世纪提出的新型机器学习算法,能在筛除不相干点参数的基础上,保留核心特征向量,具有明显的预测优势,因此,利用其构建趋势项预测模型。若基坑变形数据表示为{xt,yt}(t=1,2,…,n),可将RVM模型的输出定义为:
式中:ot为预测值;n为监测样本数;wi为权重向量;K(x,xi)为核函数;w0为偏差向量;εi为噪声。
但是,在RVM 模型的应用过程中,核函数类型、连接权值等参数一定程度上依赖使用者的经验,因此,为保证RVM 模型的参数最优性,提出对其进行优化处理。由于SFLA 算法是一种较优的仿生优化算法,具启发式协同搜索能力,其核心思想是:将优化问题看作为一个青蛙种群的寻优问题,即将青蛙群体划分为若干子群,各子群间再进行搜索和信息交换,以实现全局寻优。因此,利用其实现RVM 模型的参数寻优是可行的。
结合SFLA 算法的基本原理,可将其优化流程总结如图1所示。
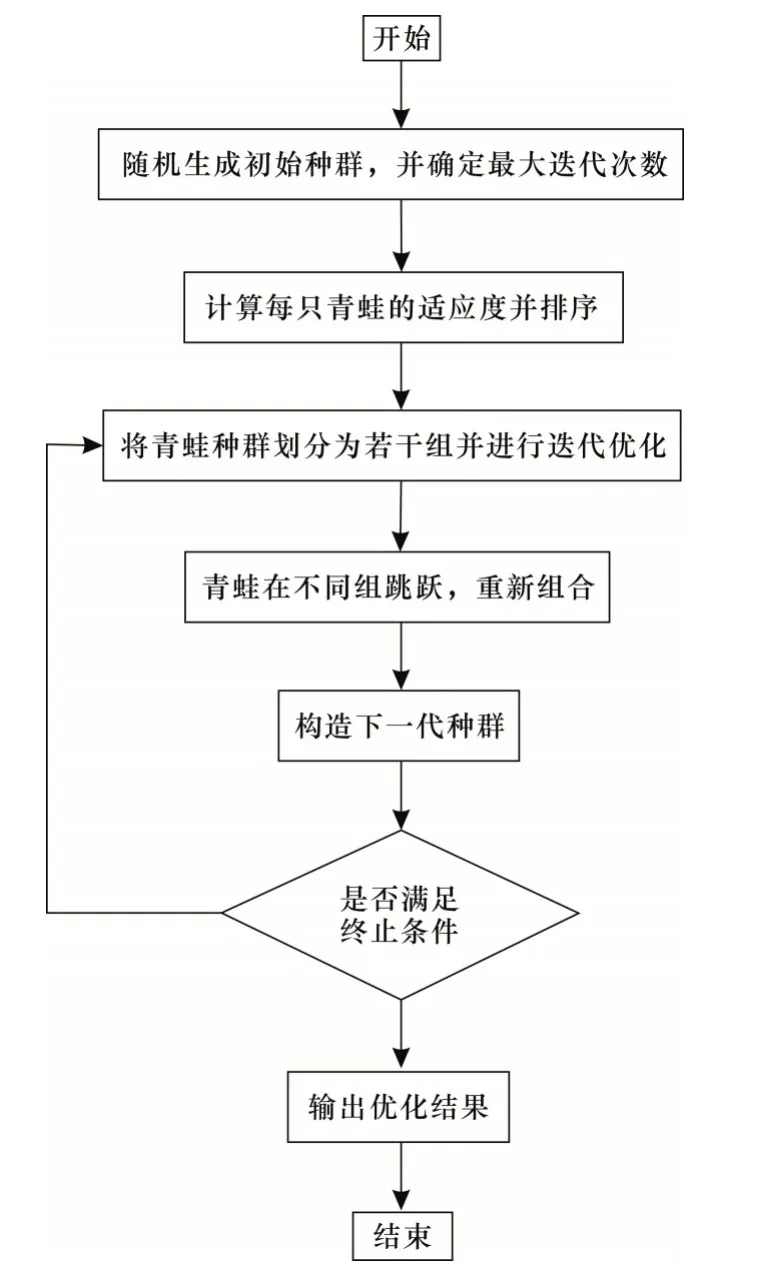
图1 SFLA算法的流程Fig.1 Flow chart of SFLA algorithm
标准SFLA算法的距离更新方式为:
式中:R为0~1间的随机量;Xb为局部最好解;Xw为局部最差解。
但是,由于标准蛙中的最次蛙可能被限制位置,使得其可能被限制搜索范围,降低了收敛速度,易出现早熟现象。为解决该问题,按照李涧鸣等(2018)的思路,引入改进SFLA算法,即ISFLA算法,其距离更新方式为:
式中:Pw为Xw经过的最佳位置。
经过ISFLA 算法优化处理有效保证了RVM 模型的参数最优性,因此,以ISFLA-RVM 模型实现趋势项预测。
1.2.2 随机项预测模型
为充分保证预测精度,将趋势项预测误差与随机项相加,组成新的随机项序列,且GRNN 模型是20 世纪由Specht 提出的改进型神经网络,其具有较强的非线性逼近能力,因此,提出利用其构建随机项序列的预测模型。
结合GRNN 模型的基本原理,其网络拓扑结构主要可分为四层,即包括输入层、隐含层、求和层及输出层,并将各层的功能分述如下:
(1)输入层主要是接受输入信息,其节点个数与输入维度相同。
(2)隐含层节点与输入层节点一一对应,其激励函数多为高斯函数,公式为:
式中:hi为隐层节点输出值(对应第i个节点处的);m为输入向量;wi为隐层训练向量;S为光滑因子。
(3)求和层比输出向量多1个维度,并在其训练过程中,主要构建出如下两参数:
式中:A为求和参数;q为隐层节点数;Gj为求和变化参量;kij为求和层训练向量。
(4)输出层主要是输出预测结果,即:
式中:zj为预测结果。
最后,将GRNN 模型预测结果与趋势项预测结果相加,即为基坑变形的组合预测值。
1.3 对比验证模型的构建
为验证本文组合预测模型的有效性,提出了两种对比验证思路:
其一,是选取多个监测点进行本文模型的预测研究,以相互对比本文预测模型的有效性。
其二,考虑到传统GM(1,1)模型、支持向量机和BP神经网络已被广泛应用于基坑变形预测中,因此,提出再以此三类模型进行类似预测,并将预测结果与本文预测结果对比,以佐证本文预测模型的效果。
2 实例分析
2.1 工程概况
吉林省医院大楼基坑位于长春市信义路和红旗街的相交处,开挖深度为17.4 m,属超深基坑,其支护设计等级为一级,主要采用“桩锚+喷砼”支护。基坑周边建、构筑物较多,加之管线广泛分布,在基坑土体连续开挖过程中,易导致建、构筑物和管线的形变,因此,基坑施工过程中的变形控制显得格外重要。
结合设计资料,基坑周长为363.7 m,拐点相对较多,造成基坑周边边长变化差异较大,因此,在基坑变形监测过程中,共拟布设了四个测量基准点,22 个水平位移监测点。限于篇幅,难以对所有监测点均进行分析,考虑到西侧基坑边较为平直,并紧邻医院6#楼,因此,以此边5 个监测点(JC18~JC22,监测点由南向北展布)为数据来源,开展本文组合预测模型的适用性验证。基于监测成果,各监测点共计监测了29个周期,统计各监测点的现有最大变形值如图2 所示。由图2 可见,基坑不同位置的水平位移值存在一定差异,其中,JC19 监测点的位移值相对最大,已达22.30 mm,而JC22 监测点的位移值为18.90 mm,相对最小。因此,得出基坑西侧水平位移的变形范围较小,差值仅3.40 mm,且此边由南至北,水平位移值具先增加后减小的规律,即此边中部的水平位移值相对更大。

图2 各监测点累计变形值对比Fig.2 Comparison of cumulative deformation values of various monitoring points
同时,再对各监测在各周期的水平位移值进行统计,详见表1。由表1可见,随监测时间持续,各监测点的水平位移值呈持续增加趋势,且大致前期具相对更大的变形速率。由于基坑水平位移值具持续增加趋势,侧面说明了开展基坑变形预测研究的必要性,即能更好地掌握基坑变形发展规律。
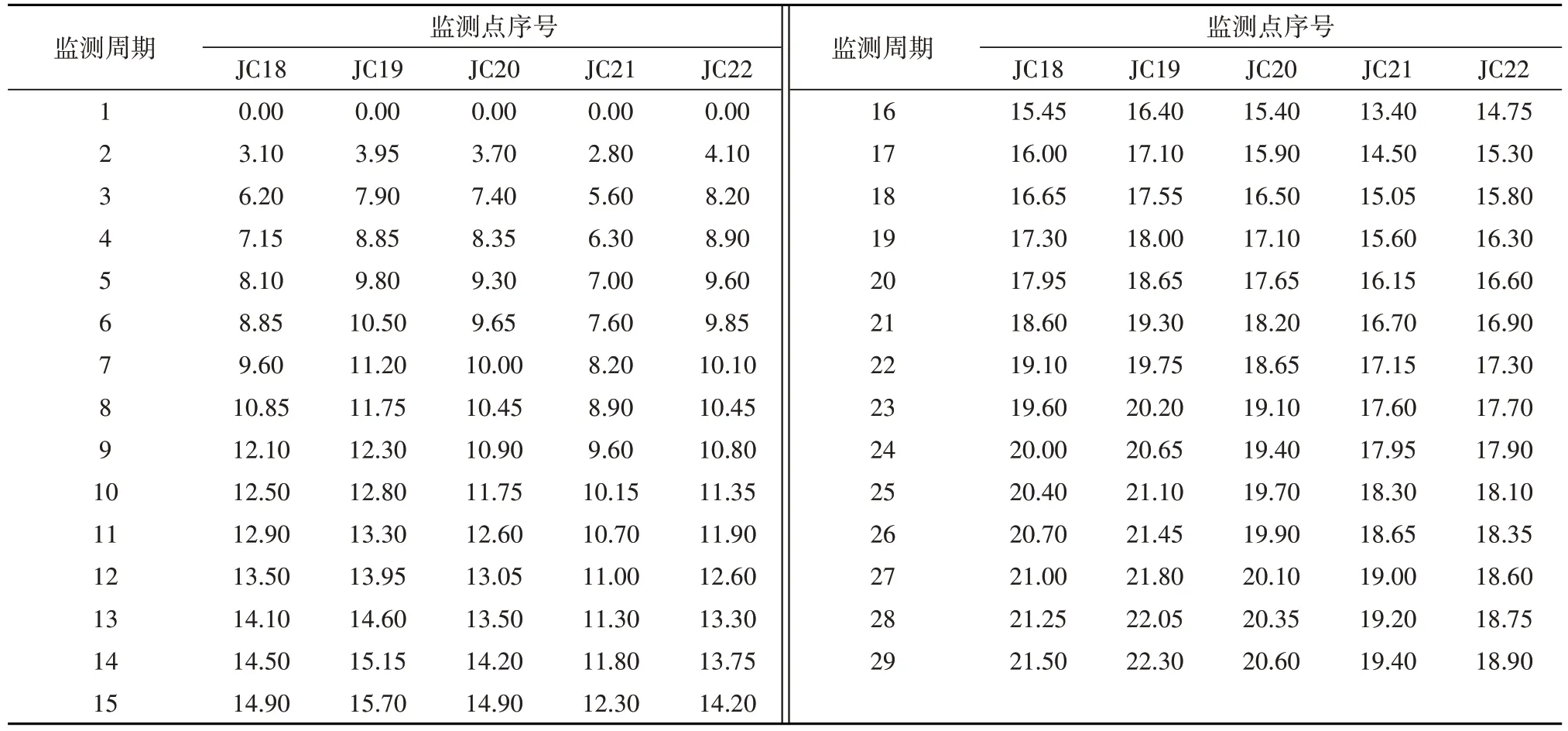
表1 各监测点的水平位移值统计(mm)Table 1 Statistics of horizontal displacement values(mm)of monitoring points
2.2 变形预测研究
根据前述,本文变形预测模型包含了三个阶段,即数据分解处理、组合预测及对比性验证,三者的具体结果如下。
2.2.1 数据分解处理效果评价
在基坑水平位移数据的分解处理过程中,为尽可能地探讨本文分解思路的合理性,对ICEEMDICA 准则各优化组合阶段的分解效果指标均进行统计,以对比递进优化过程的有效性,结果见表2。由表2 可见,从EMD 模型至ICEEMD 模型再至ICEEMD-ICA 模型,信噪比指标逐步变大,而均方根误差指标逐步减小,说明随着ICEEMD-ICA 准则的逐步构建,分解效果越来越好,充分验证了ICEEMD-ICA 准则在构建过程中的合理性。对比ICEEMD 模型和EMD-ICA 模型的分解结果,以前者分解效果相对略优,侧面说明本文分解准则构建过程中的流程也很重要,不能随意处理。

表2 不同阶段的分解效果指标统计Table 2 Statistics of decomposition effect indicators in different stages
总结本节分析结果,得ICEEMD-ICA 准则具有较优的分解效果,优于传统分解模型,能将基坑变形数据合理分解为趋势项和随机项。
2.2.2 组合预测结果分析
在前述基坑变形数据分解处理基础上,本节再进一步开展基坑变形的组合预测研究。在基坑组合预测过程中,先以JC18 监测点为例,分述不同组合阶段的预测结果,再对其余监测点进行最终预测结果统计;在预测过程中,将1~24 周期数据作为训练集,24~29期数据作为验证集,外推周期数为4期。
(1)JC18监测点的预测结果分析
首先,进行JC18 监测点的趋势项预测,且为充分验证ISFLA 算法的优化效果,分别构建了三种趋势项预测模型,即RVM 模型、SFLA-RVM 模型和ISFLA-RVM 模型,经统计,得三者的预测结果如表3所示。由表3可见,三类模型的预测效果存在显著差异,其中,在RVM 模型的预测结果中,相对误差变化范围为3.07%~3.28%,平均相对误差为3.12%;在SFLA-RVM 模型的预测结果中,相对误差变化范围为2.40%~2.76%,平均相对误差为2.61%;在ISFLARVM 模型的预测结果中,相对误差变化范围为2.08%~2.19%,平均相对误差为2.14%;三者结果对比,得出ISFLA-RVM 模型具有相对更高的预测精度。
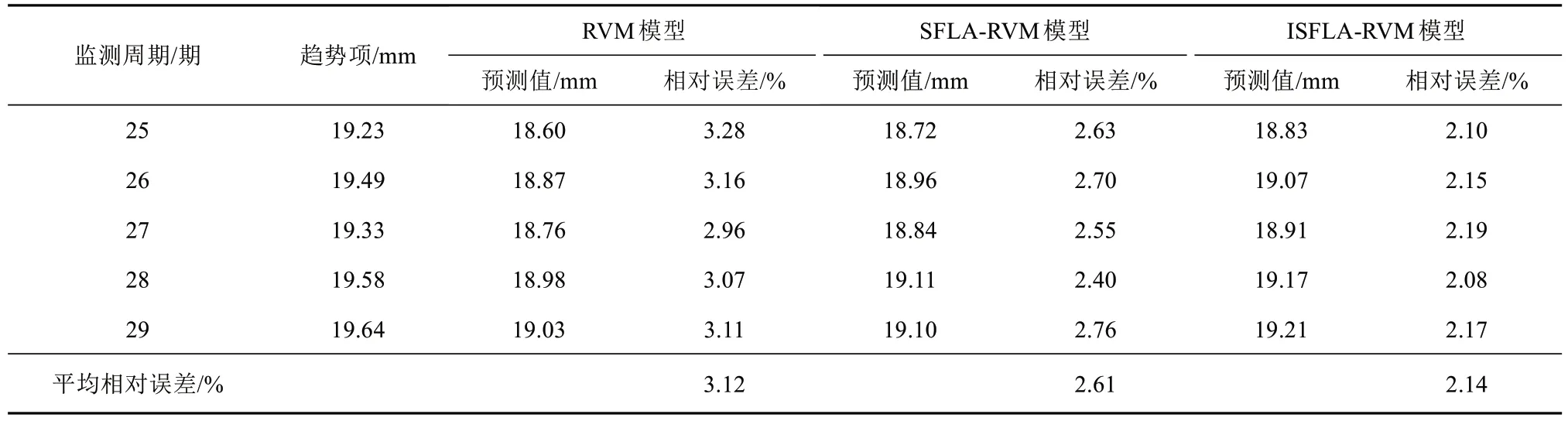
表3 JC18监测点的趋势项预测结果Table 3 Trend item prediction results of JC18 monitoring points
其次,在趋势项预测基础上,再利用GRNN模型开展随机项预测,所得结果如表4所示。由表4可见,在JC18监测点的最终预测结果中,相对误差变化范围为1.88%~2.07%,平均相对误差为1.99%,不仅具有较高的预测精度,还优于趋势项的预测效果,初步验证了本文组合预测模型的有效性;根据JC18监测点在30~33周期的外推预测,得出JC18监测的水平位移仍会进一步增加,但增加幅度相对较小。
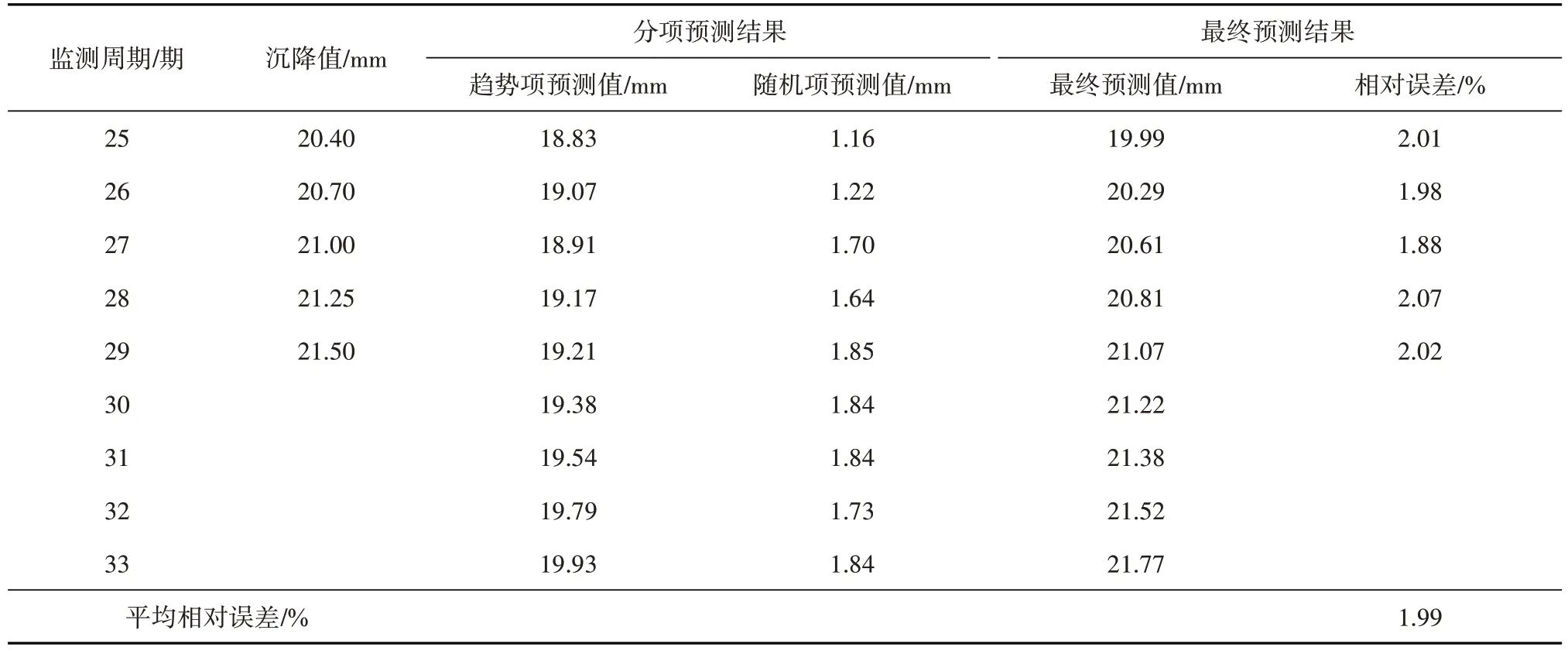
表4 JC18监测点的最终预测结果Table 4 Final prediction results of JC18 monitoring points
为进一步验证本文组合思路的合理性,再以训练时间为评价指标,开展了预测模型的训练速度研究,且将组合过程的对比模型划分为:组合阶段1,通过RVM 模型直接开展基坑变形预测;组合阶段2,通过ISFLA-RVM 模型直接开展基坑变形预测;组合阶段3,通过ISFLA-RVM-GRNN 模型开展基坑变形的组合预测。
经统计,组合阶段1 至组合阶段3 的训练时间依次为96.52 ms、85.44 ms 及61.41 ms,因此,随组合阶段的深入,对应预测模型的训练时间由96.52 ms减少至61.41 ms,说明收敛速度越来越快。
总结本节前述分析结果,得ISFLA-RVMGRNN 模型不仅能实现基坑变形的高精度预测,还具较快的收敛速度。
(2)剩余监测点的预测结果分析
再利用ISFLA-RVM-GRNN 模型对JC19~JC22监测点进行组合预测,所得结果如表5所示。由表5可见,在JC19~JC22监测点的预测结果中,所得相对误差均不大,其中,最大的相对误差值为2.11%,最小的相对误差值为1.92%,平均相对误差的变化范围为1.97%~2.07%,进一步验证了ISFLA-RVMGRNN 模型具有较优的预测效果。在此四个监测点的外推预测结果中,变形均是呈小速率增加,与前述JC18监测点的预测结果一致。
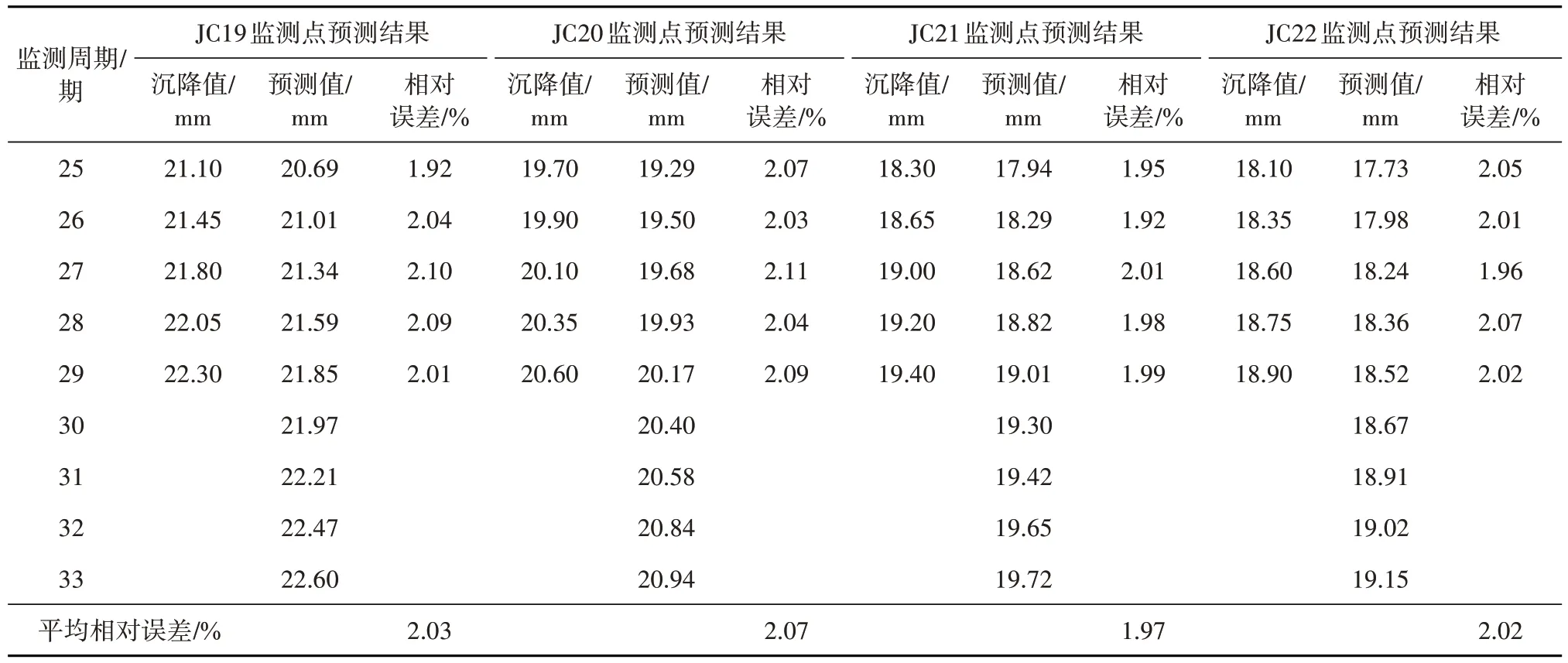
表5 剩余监测点的预测结果Table 5 Prediction results of remaining monitoring points
为进一步评价基坑水平位移的发展趋势,基于五个监测点的外推预测结果,按JC18监测点至JC22监测点的顺序,统计其30 期至33 期的变形速率均值依次为0.18 mm/周期、0.19 mm/周期、0.19 mm/周期、0.18 mm/周期及0.16 mm/周期;各监测点在外推预测结果中的速率均值主要间于0.16 mm/周期~0.19 mm/周期,均相对偏小,得到基坑水平位移后续呈小速率增加,且趋于稳定方向发展。
总结本节分析结果,得本文组合预测思路具有较优的预测效果,并经外推预测,得基坑水平位移仍会进一步增大,但总体增加速率较小,趋于有利。
2.2.3 预测效果的对比性验证
结合前述对比验证模型的构建思路,本节再利用传统GM(1,1)模型、支持向量机和BP神经网络对基坑变形进行类似预测,并以预测结果的平均相对误差和训练时间为指标,开展对比评价。经统计,结果如表6所示。由表6可见,各监测点在不同预测模型中的统计指标存在一定差异,按其平均值,在训练时间方面,本文预测模型<SVM模型<GM(1,1)模型<BP神经网络模型;在平均相对误差方面,本文预测模型<BP神经网络模型<SVM模型<GM(1,1)模型。两者综合,得出本文预测模型不仅具有相对更高的预测精度,还具有更快的训练速度,因此,得出本文预测模型相对其余三种预测模型具有更优的预测效果。
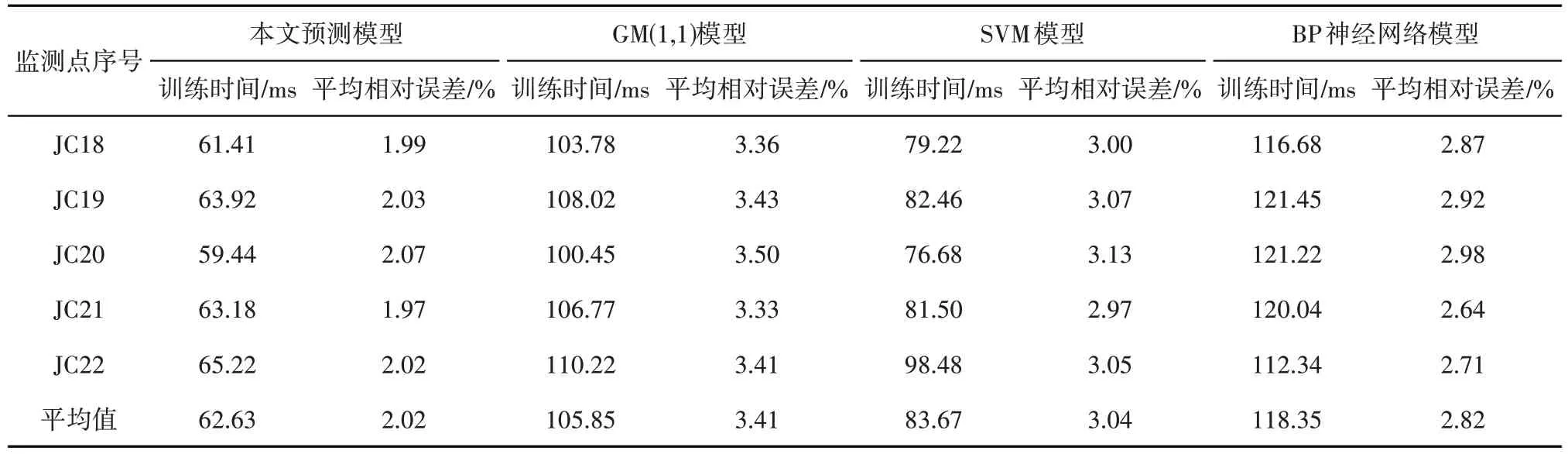
表6 不同预测模型的对比统计结果Table 6 Comparative statistical results of different prediction models
总结本节分析结果,得本文预测模型较传统预测模型具有更优的预测效果,侧面验证了前述预测结果具有较高的可信度。
3 结论
通过对吉林省医院大楼基坑的组合变形预测研究,主要得出如下结论:
(1)基坑变形数据中的随机信息会一定程度上影响其预测效果,而ICEEMD-ICA 准则具有较优的分解能力,可有效地将基坑变形数据分解为趋势项和随机项。
(2)ISFLA-RVM-GRNN 模型在本文实例预测过程中,具有较高的预测精度,所得预测结果显示,基坑水平位移仍会进一步增大,但总体增加速率较小,趋于稳定方向发展。
(3)通过不同模型预测效果的对比性验证,得出本文预测模型在预测精度和训练速度方面均具有显著优势,验证其较传统预测模型具有更优的预测效果,适用于基坑变形预测。
