由算例理解电磁场等效定理
2023-10-07汤一铭
张 明 汤一铭 包 扬
(南京邮电大学 电子与光学工程学院、柔性电子学院, 南京 210023)
电磁场等效定理最早由Love[1]提出,后经Schelkunoff[2]扩展,已在电磁场计算中得到广泛应用[3-4]。Harrington在其著作《Time Harmonic Electromagnetic Fields》[5]中给出了场等效定理的一般形式,自此场等效定理已逐渐成为大学和研究生阶段“电磁场理论”课程教学的重要内容之一[6-8]。然而对于初学者,难以在其众多的变化中找到规律并应用于电磁场计算。
本文通过简单场景电磁场问题的多种等效问题,从数学和物理两方面解释电磁场等效定理,案例形象直观,有助于初学者完整理解场等效定理。
最后将其推广到一般形式,用两个电磁场散射问题说明电磁场等效定理一般形式的使用方法,为学生在今后应用场等效定理解决实际电磁场问题计算时提供参考。
1 电磁场边界条件和唯一性定理
在讨论电磁场等效定理之前,先回顾电磁场切向分量的边界条件及电磁场唯一性定理[7]。
1.1 边界条件
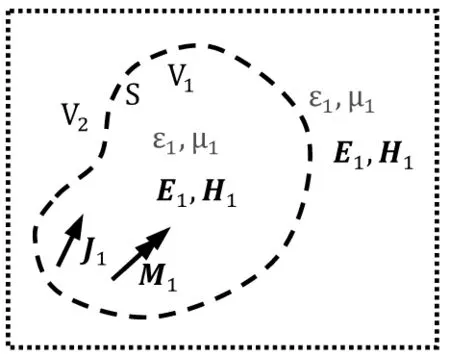
如图1所示,曲面S将媒质1(介电常数和磁导率分别为ε1和μ1)和媒质2(介电常数和磁导率分别为ε2和μ2)分为两个区域,分界面两侧的电磁场分别为E1,H1和E2,H2。如在媒质分界面上有面电流密度JS和面磁流密度MS,则分界面两侧电场强度和磁场强度的切向分量分别满足

图1 电磁场切向分量的边界条件
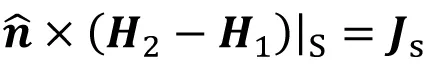
(1)
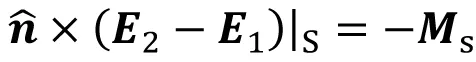
(2)
由边界条件(1)和(2)可知:
(1)如果分界面上不存在面电/磁流,则分界面两侧电/磁场强度的切向分量保持不变,或分界面两侧电/磁场强度的切向分量连续。
(2)如果人为改变某一侧电/磁场的切向分量,则会造成分界面两侧电/磁场强度的切向分量不连续,此时必须有相应的面电/磁流出现,以弥补分界面两侧电/磁场强度的切向分量不连续造成的差。这是场等效定理的操作依据。
1.2 电磁场唯一性定理
电磁场等效定理源自电磁场唯一性定理。以时谐场为例,电磁场唯一性定理为:
(1)区域边界上电场强度E的切向分量确定;
(2)区域边界上磁场强度H的切向分量确定;
(3)区域部分边界上电场强度E的切向分量确定,剩余边界上磁场强度H的切向分量确定。
三个条件只要满足其中任意一个,则该区域内由电流源Ji和磁流源Mi产生的电磁场E和H是唯一的。
电磁场唯一性定理为场等效定理提供了理论基础,即只要保证区域内电/磁流源不变,区域内媒质不变,区域边界上的边界条件不变,则区域内的电磁场就不变,而区域外的场和媒质可以按需要变化(选择)。
2 Love场等效定理
首先看一个最基本的场等效问题。
2.1 Love场等效的原问题
如图2(a)示,在整个空间有媒质(ε1,μ1),电流源J1和磁流源M1在整个空间产生的电磁场为E1和H1。现用一封闭曲面S包围电/磁流源,曲面S将空间分为含电/磁流源的区域V1,和不含源的区域V2。
(a)原问题
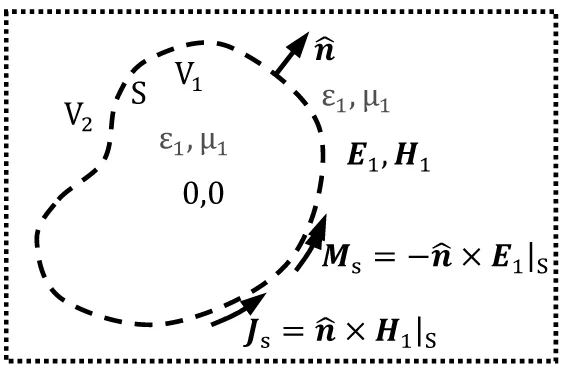
(b) 区域V2的等效问题图2 Love电磁场等效原理
2.2 V2区域场等效问题
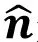
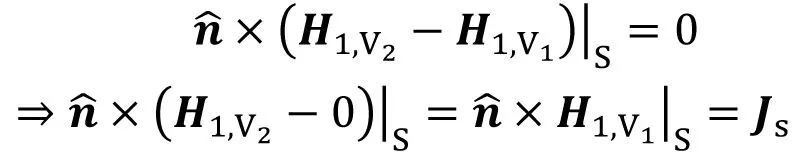
(3)
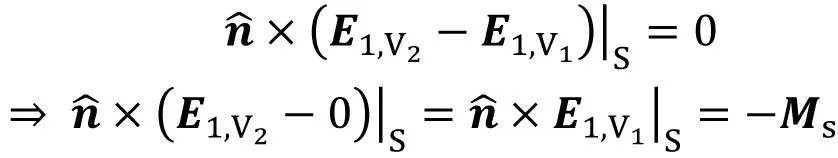
(4)
式中H1,V1和H1,V2分别是表面S两侧的磁场强度,由原问题可知,H1,V1︳S=H1,V2︳S=H1︳S;同理E1,V1︳S=E1,V2︳S=E1︳S。因此,V2区域内的电磁场E1,H1可以看成是由S面的等效面电流密度Js和等效面磁流密度Ms在整个空间都是媒质(ε1,μ1)情况下产生的。因为对于V2区域而言,等效前后区域内电/磁流源没有发生变化(都不存在电/磁流源),区域边界S上,电/磁场强度切向分量等效前后没有发生变化,根据电磁场唯一性定理,等效问题V2区域内的电磁场与原问题一样。
我们还可以理解为,原问题V2区域内的电磁场是V1区域的电磁场通过S面“传递”到V2区域,等效问题将V1区域的电磁场设为零,V1区域无电磁场通过S面“传递”到V2区域,则需要在S面上添加等效源来产生V2区域的电磁场。电磁场唯一性定理和边界条件保证了S面上(3)和(4)所示的等效源在V2区域产生与原问题一样的电磁场。
3 一个特殊场景的电磁场等效问题
为了检验上述场等效定理,Rengarajan[9]用无限空间向+z方向传播的均匀平面电磁波为例,等效z>0半空间的电磁场,及在z=0平面上的等效电/磁流。为便于进一步扩展,现将其复述如下。
3.1 原问题
如图3(a)所示,整个空间媒质参数为(ε,μ),极化为+x的沿+z方向传播的均匀平面波可表示为
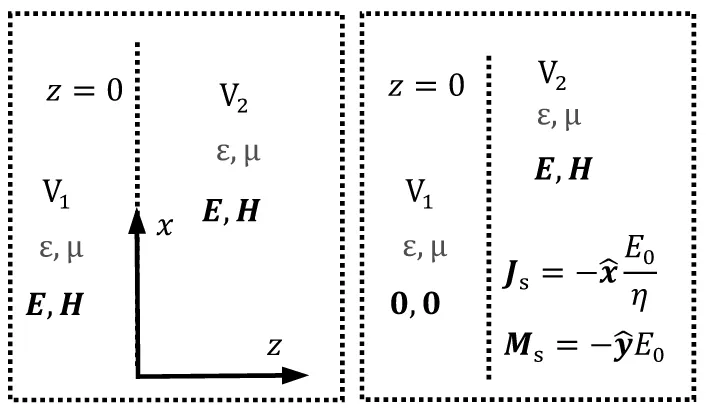
(a)原问题 (b)V2区域等效问题1图3 场等效原理算例
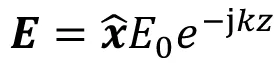
(5)
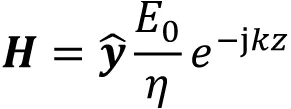
(6)
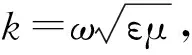
3.2 等效问题1
如图3(b)所示,将z<0半空间的电磁场设为零,根据式(3)和(4),在z=0平面上的等效电/磁流源为
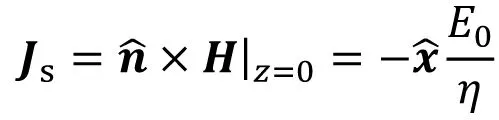
(7)
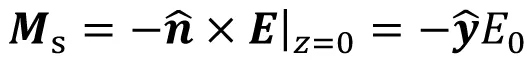
(8)
由电/磁流源JS和MS产生的电磁场分别如表1和表2所示。
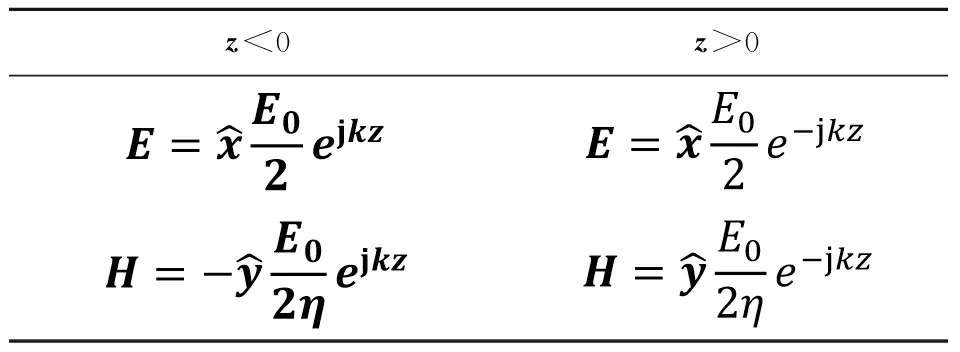
表1 z=0平面上等效面电流源JS产生的电磁场

表2 z=0平面上等效面磁流源Ms产生的电磁场
表1和表2电磁场的具体计算见文献[9]附录。由表1和表2很容易发现,等效面电/磁流源在z<0区域产生的总电/磁场为零,而在z>0区域产生的总电/磁场恰好是公式(5)和(6)表示的原问题的电磁场。
电磁场唯一性定理并未对V1区域的媒质和电磁场做限制,因此V2区域可以有更多的等效。
3.3 等效问题2
如图4(a)所示,z<0半空间设为理想电导体(perfect electric conductor PEC),内部电磁场为零,在z=0平面上的等效电/磁流源也为式(7)和(8)所示。此时V2区域内的电磁场等效为z=0(PEC平面上)的等效面电/磁流密度所产生。应用电磁场互易定理可知PEC表面的电流不产生辐射[9],而磁流源产生的电磁场可利用无限大PEC表面的镜像法[7],即V2区域内的电磁场由移去理想电导体后两倍式(8)所示磁流源产生。利用表2的公式,容易得到与式(5)和(6)相同的电磁场。
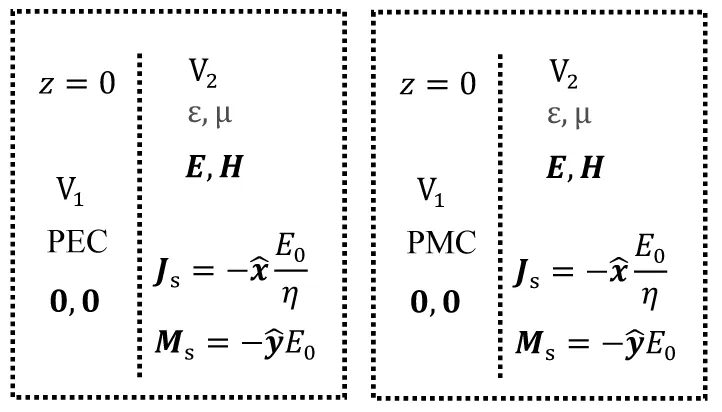
(a) V2区域等效问题2 (b) V2区域等效问题3图4 场等效原理算例
3.4 等效问题3
如图4(b)所示,z<0半空间设为理想磁导体(perfect magnetic conductor PMC),电磁场为零,在z=0平面上的等效电/磁流源也为(7)和(8)。由互易定理知PMC表面的磁流不产生辐射,利用无限大PMC表面的镜像法[7],V2区域内的电磁场由移去PMC后两倍式(7)的电流源产生。由表1的公式可得此等效的电磁场与式(5)和(6)相同。
3.5 等效问题4
如图5(a)所示,将z<0半空间改为与原媒质不同的另一种媒质(ε1,μ1),电磁场设为零。在z=0平面上的等效电磁流源还是如式(7)和(8)所示。V2区域的电磁场等效问题描述为:整个空间由媒质(ε1,μ1)和媒质(ε,μ)各占一半,分界面是z=0,在媒质(ε1,μ1)的表面上有式(7)和(8)所示的等效面电/磁流源,这一对电/磁流源在V2区域将产生与原问题一样的电磁场。请注意此时与等效问题1不同,整个空间不是同一种媒质,不能直接用表1和表2所示的计算结果(因为不能用无界空间的格林函数积分得到电/磁流源的磁/电矢量位)。

(a)V2区域等效问题4 (b)V2区域等效问题5图5 场等效原理算例
要计算半空间表面上的电/磁流源产生的电磁场需要使用半空间表面上的格林函数[10],这里我们用表1和表2的结果分析推算。将图5(a)中电/磁流源从z=0移到z=z0,z0>0,计算此时电/磁流源在z>z0空间的电磁场,然后让z0→0,即是V2区域的等效电磁场。
z=z0处的电/磁流在0
值得注意的是,比较等效问题4和等效问题1,两者等效面电/磁流密度一样,但在V1区域的媒质不同。等效问题1中V2区域的场由等效面电/磁流源在全空间相同媒质情况下产生。而等效问题4中,V2区域的场由与等效问题1相同的电/磁流源在半空间为媒质(ε1,μ1),半空间为媒质(ε,μ)情况下产生。但在V2区域,两种等效问题的场与原问题一样。
3.6 等效问题5
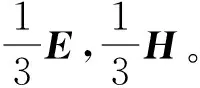
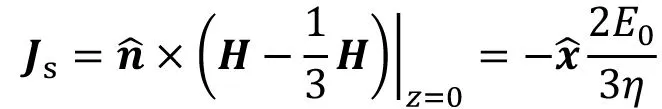
(9)
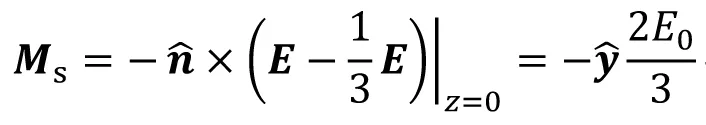
(10)

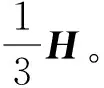
由以上等效问题的讨论可得如下结论:
(1)被等效区域外的媒质可任意假设;
(2)被等效区域外的电磁场可任意假设,但必须为该区域电磁场问题的真实解;
(3)被等效区域内的场由三部分叠加而成:①区域内原本的源产生的场;②边界等效源产生的场;③边界外“传递”进来的场(等效问题中区域外未设成零场的情况)。
4 电磁场等效定理一般形式
至此可将电磁场等效定理推广到一般形式[5]:
4.1 原问题a

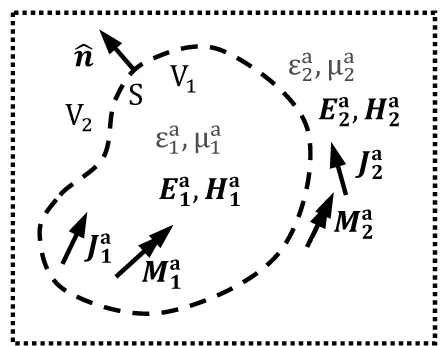
(a) 原问题a

(b) 原问题b
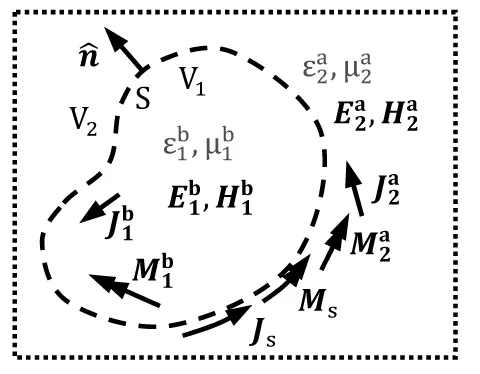
(c) 等效问题1

(d) 等效问题2图6 电磁场等效原理一般形式
4.2 原问题b

4.3 等效问题1
如图6(c),V1区域等效原问题b,同时V2区域等效原问题a,等效面电/磁流密度为
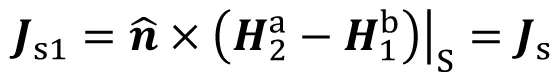
(11)

(12)
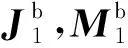
4.4 等效问题2
如图6(d),V1区域等效原问题a,同时V2区域等效原问题b,等效面电/磁流密度为
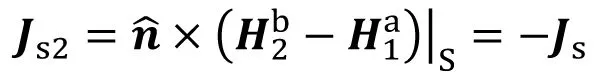
(13)
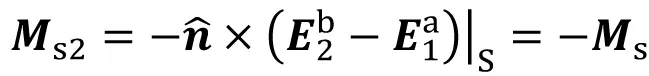
(14)
上两式中用到原问题a和b的边界条件。各区域产生的场分析类似于等效问题1。
最后以理想电导体和介质体的电磁散射问题为例,说明如何使用上述电磁场等效定理的一般形式。
4.5 PEC目标散射
设自由空间(ε0,μ0)一均匀平面电磁波入射到一PEC目标上,电磁场在PEC内部为零,PEC外的总场包括入射场和PEC产生的散射场。为计算PEC目标的散射场,应用电磁场等效定理一般形式如下:
原问题a:V1区域为导体,场为零,无源;V2区域为媒质(ε0,μ0),电/磁流源产生均匀平面波,即是入射场。
原问题b:整个空间都为媒质(ε0,μ0),电磁流源为零,场为零。
应用等效问题1中V2区域等效,V1区域为原问题b的媒质,与V2区域媒质一样,整个空间为媒质(ε0,μ0)。根据原问题a的边界条件:PEC表面电场强度的切向分量为零,因此S表面的等效磁流源为零。等效面电流密度为
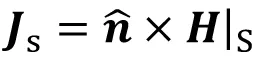
(15)
式中H为PEC表面的总磁场强度。由理想电导体表面边界条件得散射电场强度的切向分量等于入射电场强度切向分量的负值,
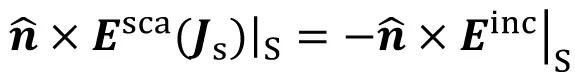
(16)
其中V2区域原本的源产生入射场Einc为已知。散射场由等效面电流密度JS产生,等效问题的整个空间为媒质(ε0,μ0),使用自由空间格林函数,可写出由JS计算散射电场的表达式Esca(JS)[5]。代入式(16)即为理想电导体的电场积分方程。用矩量法[12]解出JS,就可计算散射电磁场。
4.6 介质体散射
设自由空间(ε0,μ0)中一均匀平面波入射到一均匀介质体(ε,μ)上,在介质体内电磁场为总场(E1,H1),介质体外的电磁场(E2,H2)包括了入射场和介质体产生的散射场。为计算介质体的散射场,应用电磁场等效定理的一般形式如下:
原问题a,V1区域为介质体(ε,μ),场为(E1,H1),无源;V2区域为自由空间(ε0,μ0),电磁流源产生均匀平面电磁波,即是入射场。
原问题b,V1区域为自由空间(ε0,μ0),无源,场为零;V2区域为介质 (ε,μ),源和场都为零。
应用等效问题1中V2区域等效,V1区域为原问题b的媒质(ε0,μ0),与V2区域的媒质一样,因此整个空间为同一媒质(ε0,μ0)。根据原问题a的边界条件,表面S内外电/磁场强度的切向分量连续。等效面电/磁流密度为

(17)

(18)
式中H2|S为S表面的总磁场强度,E2|S为S表面的总电场强度。由于在此等效问题中,整个空间都是媒质(ε0,μ0),可以写出用自由空间格林函数计算V2区域内散射电磁场的计算式[11],简记为Esca(JS,MS)和Hsca(JS,MS)。
再应用等效问题2中V1区域等效,V1区域为原问题a的均匀介质体(ε,μ),V2区域的媒质为原问题b的(ε,μ),此时整个空间都是媒质(ε,μ)。V1区域内是总场(E1,H1),V2区域的场为零。S表面的等效面电/磁流密度分别为-JS和-MS,用媒质(ε,μ)完整空间的格林函数可写出这对电磁流源在V1区域产生总场表达式,简记为E1(-JS,-MS)和H1(-JS,-MS)。最后利用S表面的边界条件得电磁场积分方程

(19)
和
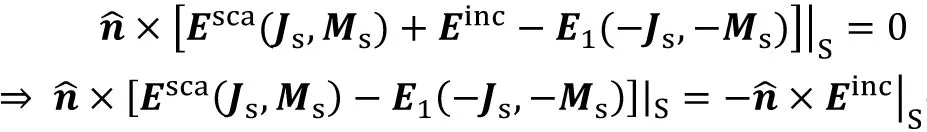
(20)
上述两积分方程右端入射场为已知,用矩量法[12]解出JS和MS,并由JS和MS计算散射场。
在实际应用中,为了计算简便,常用两种等效问题:
原问题整个空间不是同一媒质,等效后为同一媒质,由此可使用完整空间的格林函数。在计算喇叭和抛物面口径天线辐射时常使用该等效方法。
分界面为无限大平面时,可将非计算区域等效为半空间的PEC或PMC,由此可使用镜像法。此等效方法在计算缝隙天线辐射,腔体散射等问题时常被应用。
5 结语
电磁场等效定理过于理论和抽象,是电磁场理论教学中的难点之一。本文通过一个典型算例演示了多种电磁场等效问题,形象直观,有助于理解抽象的理论并改善教学效果。最后引入电磁场等效定理的一般形式,通过举例说明其应用,可帮助学生将来应用场等效定理计算电磁场问题。
