平面波与高斯函数或样条函数复合基组*

张广迪 毛力2)† 徐红星2)3)4)‡

1) (武汉大学物理科学与技术学院,武汉 430070)

2) (武汉量子技术研究院,武汉 430205)

3) (武汉大学微电子学院,武汉 430072)

4) (河南省科学院,郑州 450046)

通过将平面波与高斯函数或者样条函数结合到一起,本文构建了一种新的复合基组.利用格拉姆-施密特正交化方法或者Löwdin 正交化方法,对复合基组进行正交归一化.通过选择平面波函数中波矢的绝对值,选择性地求解某个能量区间内的本征态,将大型哈密顿矩阵的计算转变为多个小型矩阵的计算,以及通过减少电子势能平缓部分展开基矢数目,极大地加快了计算速度.以一维有限深势阱为例,通过与严格计算方法的对比,验证了本文复合基组能够在加速计算的情况下保证求解精度.同时,本文还研究了不同的参数设置对计算精度的影响,包括复合基矢的疏密度、高斯函数的宽值,以及样条函数不同区域占函数总宽度的比值等参数.最后该复合基组可以直接应用到对大尺寸纳米金属结构的等离激元数值计算当中.

1 引言

金属微纳结构(纳米金属棒、颗粒或板)间的纳米间隙具有很重要的性质,在物理、化学和生物等领域都有着广泛的研究与应用[1,2],比如在表面等离激元方面的应用[3,4].表面等离激元是电磁场与固体中自由电子集体振荡强耦合形成的一种元激发,它可以将光场局域在突破衍射极限的亚波长范围内.例如金属颗粒之间的纳米间隙[5-10],人们称之为“热点”.其中的电场强度被等离激元共振增强,增强倍数甚至可以达到102,从而使得间隙内部的分子拉曼散射信号极大增强(由于拉曼信号正比于电场的4 次方,所以最大可达108),这就是表面增强拉曼光谱[11-13].一般而言间隙间距越小电场增强越大,但是间隙小到纳米尺度时量子效应会起作用[14-17],以往仅利用经典的电磁学方法计算电磁场[18-20]会失效.此时可以使用密度泛函理论进行计算[21,22],以获得更准确的结果.

密度泛函理论(DFT)[23-26]以及含时密度泛函理论(TDDFT)[27,28]是研究多电子体系的重要方法,在物理和化学的很多领域都有着广泛的应用.密度泛函理论基于Hohenberg-Kohn 定理: 给定一个在特定初始状态下的电子系统,外部的势能和电子密度之间存在着一一对应关系.相互作用电子系统的基态密度和势场分布可以由对应的无相互作用系统的Kohn-Sham 方程组的解确定.因此,密度泛函理论的关键在于快速准确地求解Kohn-Sham 方程组[29,30].然而,在实际应用中,很多器件总体尺寸在微米量级.如果使用密度泛函的方法,为了使计算结果足够准确,需要使用足够多的波函数进行展开,Kohn-Sham 方程组中的哈密顿量的矩阵维度将会非常大.以直径10 nm 长1 μm 的金纳米棒为例,电子数目将达到百万级,由于需要计算哈密顿量的矩阵元,以及对矩阵进行对角化,矩阵维度过大,此时计算量将会变得非常大(对角化矩阵的计算复杂度为O(N3) ,同时需要计算N2量级的势能积分).这样会给计算资源带来很大压力,甚至可能因为矩阵维度过大而无法计算.如果直接减少波函数的数目来加快计算速度,将会导致计算结果的误差较大.因此,急需新的算法来加快大尺度密度泛函理论的计算速度.

减小矩阵的维度有不同的方法,例如Meng等[31,32]发展了混合量子力学和经典电磁学(QM/EM)方法,将系统依据特征划分为量子区间与经典区间,在经典区间用时域麦克斯韦方程组求解.在量子力学区间用量子非平衡格林函数求解,量子力学和经典区间界面处的瞬态电势分布和电流密度分别用作量子力学和电磁模拟的边界条件.由于此时量子区间非常小,可以有效地减少矩阵维度.除此以外还可以通过基组的选取减小矩阵维度.在DFT的计算中,选取合适的基组,是一个非常重要的问题,合适的基组可以使得计算准确与快速.很多研究都在关注基组的选取,例如何禹等[33]通过研究基函数效应,找到了DFT 理论中B972-PFD 方法的最具有性价比的基组.另外将不同的基矢复合到一起,作为新的基矢对研究的系统进行展开,有时可以得到比单一基矢更好的结果.段宜武等[34]发展了少体物理中的简谐振子展开方法,引入了低能态波函数并将其与简谐振子波函数混合作为基矢,利用初步的近似波函数,与一些没有使用过的简谐振子乘积波函数乘到一起,构成新的复合基矢,从而减小基矢总数.本文将使用复合基组的方法,将平面波与高斯函数或者样条函数乘在一起来减小密度泛函理论中矩阵的维度.

在第一性原理计算中,平面波基组应用非常广泛(例如著名的VASP 软件)[35],它在处理周期系统时非常有效.然而,在开放系统中,体系尺寸往往较大,有的地方需要精确的密集数据,有些地方只需要少量的稀疏数据就可以得到较精确的结果.例如在求解银纳米棒的表面等离激元激发时,银纳米棒的两端以及表面电子势能变化快,往往需要精确计算.而纳米棒“棒芯”部分由于电子势能平缓,原则上仅需少量信息就可以描述.因此并不需要花费过多的计算资源在占比极大的中间部分.作为一种非局域基矢,平面波基组需要大量的平面波来对物理空间的所有部分进行展开,包括对我们的问题不重要的中间区域.因此选择线性复杂度的局域基组(例如高斯基组[36]),可以根据需要调整不同区域的基矢疏密度,减少所用的基矢总数,从而加快计算.尽管如此,高斯基组间的间距也是原子尺度,在介观尺度下需要的基组数目仍然非常庞大.本文基于这一点,发展了一种新型的高斯函数或含有多项式的样条函数与平面波复合的基组.这种基组同时利用高斯函数或者样条函数的局域特性,通过选择不同平面波波矢来控制求解能量区间,实现了对哈密顿矩阵的分区求解.在每一个小区间可以显著地减少使用的基矢数,在保持相应精确度的情况下实现最终的加速计算.

2 计算方法

2.1 初始复合基组

本文使用高斯函数或样条函数与平面波函数相乘,得到一组新基矢:

或样条函数,这里σ为高斯函数的宽值,xn为不同高斯函数或样条函数中心的位置,样条函数参数cij和u0由宽度参数al计算得到,高斯函数或样条函数的疏密度可以方便地进行调整.使用的高斯函数与样条函数如图1 所示.

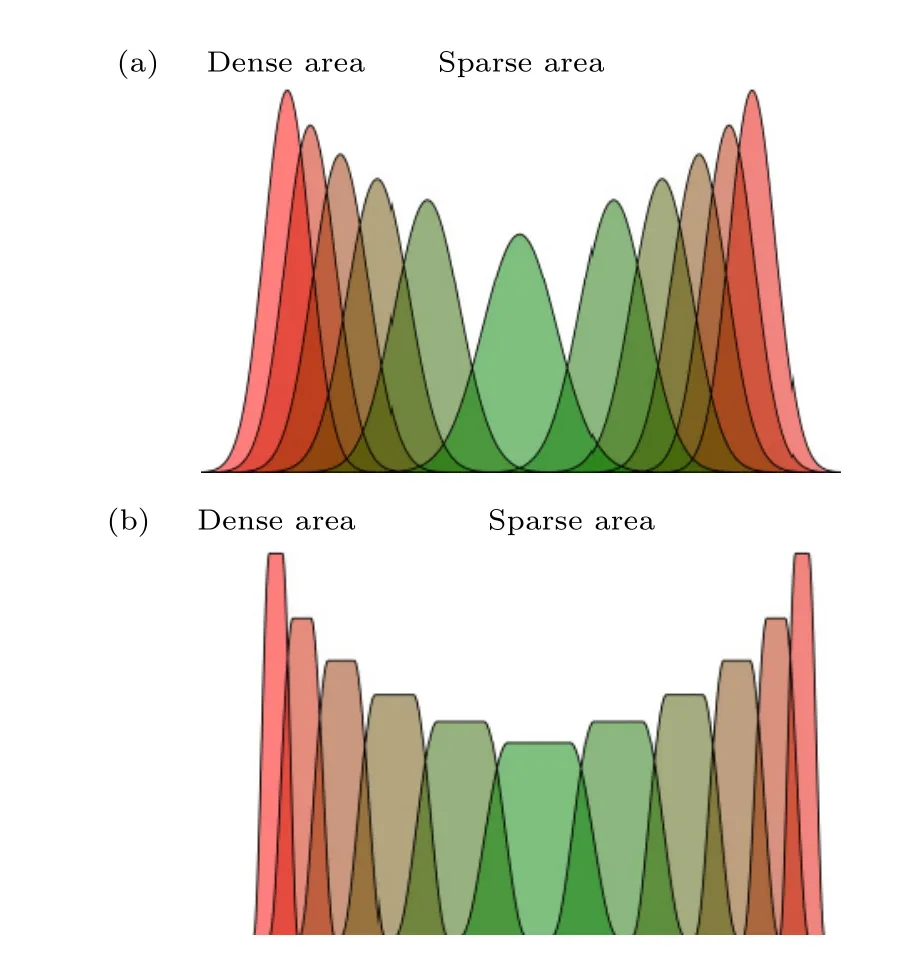
图1 用来复合的高斯函数与样条函数 (a)高斯函数;(b)样条函数Fig.1.Gaussian wave function and spline function for composition: (a) Gaussian wave function;(b) spline function.

可以通过将平面波函数与高斯函数或样条函数簇相乘得到一系列未正交归一化新基矢,即(1)式.由完备性考虑平面波波矢k应该同时选取正负某个值,通过改变k的绝对值可以选择求解的本征值区间.特定k值的平面波相当于一个在势能平缓区间的试探解,算法自动组合各局域高斯或样条函数来匹配试探解与严格解之间的k值差距.

在量子力学的相关计算中,基组的选取与构建需要遵循一定的原则.可以看出,本文的复合基组有以下特点: 首先,由基矢的傅里叶变换可知,基组在动量空间中±k附近是近似完备的;其次,基组是正交归一化的,2.2 节将进行基组的正交归一化处理;然后,基组中基矢的形式在数学上是便于积分的,高斯函数或样条函数,以及它们与平面波函数的乘积,均可以求出解析的积分结果;最后,由于复合基矢的形式中含有平面波,基矢的形式与系统波函数有一定的类似性.在满足上述原则的情况下,本文的复合基组可以很好地应用于具有电势边界变化剧烈而内部平缓这一特征的物理体系.另外,由于复合基矢同时包含空间局域化函数(高斯函数或样条函数)与空间扩展函数(平面波函数),便于通过改变高斯函数或样条函数的空间分布疏密度,以及改变平面波波矢的选取这两种途径,来加速本征值的求解.

2.2 复合基组的正交归一化

新基矢的数目需要根据系统的长度和精度要求进行调整.在进行计算前还需要对它们进行正交归一化.本文使用格拉姆-施密特正交化方法[37,38],或者Löwdin 的正交化方法[39],得到一系列新的正交归一化基矢.

格拉姆-施密特正交化方法的基本流程是,选第一个原基矢作为第一个新基矢,不断构建新的基矢,使每个新基矢与前面所有的新基矢正交,并且对新基矢进行归一化.格拉姆-施密特正交化方法可以用如下公式表示:

其中ψn为正交归一后的基矢,ϕn为原基矢,ψ1=ϕ1,由表达式可知其是一个迭代方法,直接用(4)式一般不太稳定,研究者们提出了许多改进方法,格拉姆-施密特正交化本质上等价于对矩阵做QR 分解,可以直接调用现在非常成熟的线性代数包求正交矩阵Q和系数矩阵R来计算.

Löwdin 正交化方法通过构建一个变换矩阵来把原基矢进行正交归一化:

Si为(6)式中矩阵的第i个特征值,可以得到变换矩阵:

本文使用上述两种正交化方法对复合基组进行正交归一化,并进行比较,可以发现,两种方法均可以对复合基组进行足够精确的正交归一化处理.然而由于格拉姆-施密特正交化方法需要不断地迭代,当两个基矢相距较近时,会使得分母接近于零从而导致误差的积累,需要进行更细致繁琐的参数调整来进行处理.因此本文使用Löwdin 正交化方法,或者调用科学计算库中(例如GSL)的QR分解(以代替格拉姆-施密特正交化方法),来进行正交归一化处理.

3 结果与讨论

3.1 一维有限深势阱的能级分布

利用复合基矢计算时,某些情况下有严格的解析结果,可以通过对比误差来分析它的有效性.本文利用复合基矢计算一维有限深势阱的能级分布与波函数.一维有限深势阱为

该系统有解析解[40].下面用前文得到的基矢对一维有限深势阱进行展开,求得能量值后与解析结果进行对比.

系统的哈密顿量为

其中m为电子质量,ℏ 为约化普朗克常数.用本文的复合基矢可以求得哈密顿矩阵的矩阵元为Hmn=〈ψm|H|ψn〉,将(2)式或(3)式中的函数代入其中并数值对角化即可求得能量本征值.这些计算值与理论值之间的相对误差与系统的长度、使用的基矢的数目、基矢结构参数均有关系.在图2 中横坐标为不同的本征值,纵坐标为计算值与理论值之间的相对误差,我们仅使用少量基矢,发现即使在这种情况下面相对误差也很小.但是图2 可以说明本文方法精确度非常高.计算的相对误差基本上都在10-5和 10-6的量级.可以看出,减小中间基矢的数目,从而减小总基矢的数目,仍然可以得到足够精确的结果,同时又可以明显加快计算速度.当系统的物理尺寸较大,因而需要较多的基矢总数时,3.3 节将通过调整基矢中平面波波矢的值来提高计算的效率.

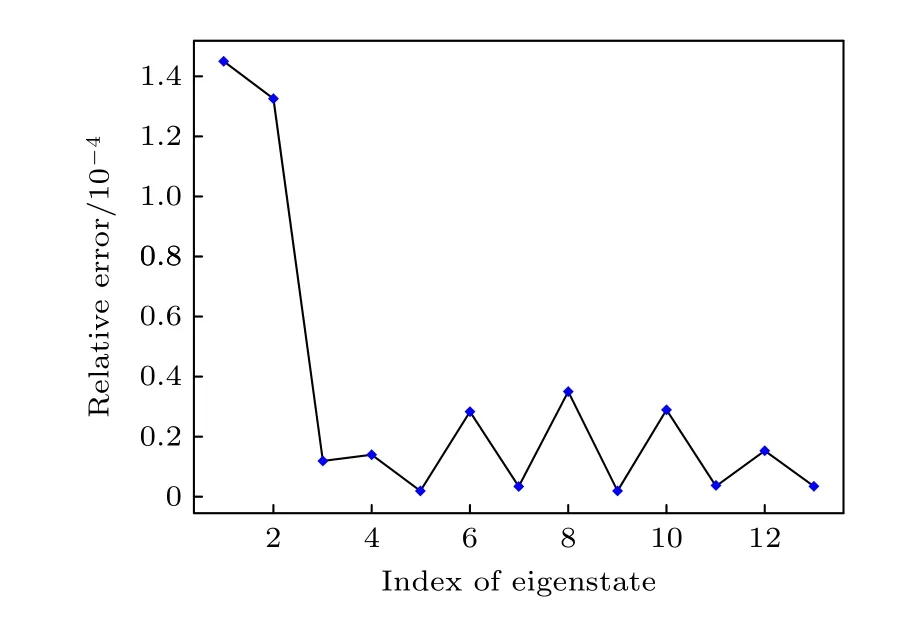
图2 仅使用少量基矢时,计算值与理论值的相对误差(x 轴为不同的本征态,y 轴为计算值和理论值之间的相对误差,后文相同)Fig.2.Relative error between calculated and theoretical values when only a small number of base vectors are used(x-axis,different eigenstates;y-axis,relative error between calculated and theoretical values;the following image is the same as the Fig.2).

3.2 不同的函数设定对精度的影响

由于高斯函数或样条函数均与坐标有关,并且可以改变高斯函数的宽值,或者分段函数各段的长度,因此,本文研究了不同的参数对新的复合基矢精度的影响.以高斯函数构成的复合基矢为例.由于本节使用了较多的基矢,计算的相对误差与2.1 节相比会有略微的不同.

首先考虑不同的疏密度比率对精度的影响.如图3 所示,横坐标为不同的本征态计数,纵坐标为计算值与理论值之间的相对误差,r为疏密度比率,疏密度比率是单位长度内系统两端(即电子势能变化快速部分)使用的基矢数与系统中间部分(电子势能平缓部分)使用的基矢数的比值.从图3 可以看出,即使在疏密度比率等于1 时,也就是系统两端部分和中间部分的基矢密度相等时,复合基矢仍然保持着较高的精度,所求的系统本征值与理论本征值之间的相对误差的数量级在 10-4的位置.而随着疏密度比率逐渐增大,相对误差逐渐减小,直到 10-5的位置.由于系统中间部分需要最低数量的基矢来展开,因此随着疏密度比率的增大,相对误差不会无限减小,在本文对应的程序里面可以根据不同的系统求出一个相对误差接近最小的疏密度比率.综上,通过调整基矢疏密度确实能够提高精度,图3 显示大约可以提高一个量级.

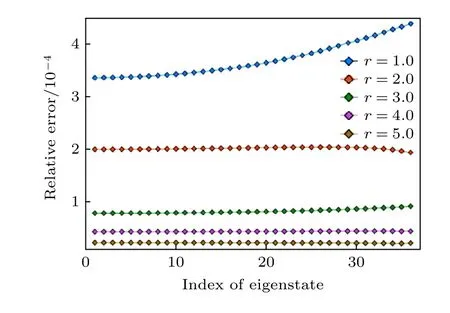
图3 不同的疏密度比率对精度的影响Fig.3.Effect of different degree of closing on precision.

接着讨论不同的基矢宽度对精度的影响.图4横坐标为不同的本征态计数,纵坐标为利用复合基矢求得的本征值与理论本征值之间的相对误差,s为基矢宽度与基矢之间距离的比值,图中疏密度比率为5.可以看出,整体的相对误差数量级在10-5的位置.相对误差随着基矢宽度变宽先减小然后增大,在疏密度比率为5 的条件下,最优基矢宽度大概为0.85 相邻基矢间距.

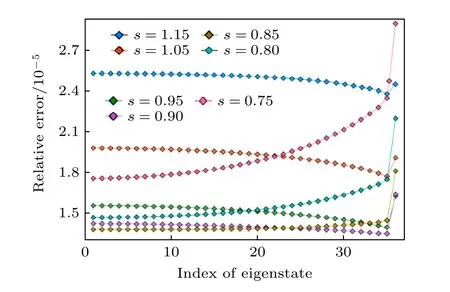
图4 不同的基矢宽度对精度的影响Fig.4.Effect of different basis sets width on precision.

对比图3 和图4 可以看出,基矢的不同疏密度比率对精度的影响,比不同的基矢宽度对精度的影响更大,疏密度比率是更具决定性的影响精度的因素.

3.1 与3.2 节仅计算了能量最低(平面波波矢k的取值为0,即不乘平面波只用局域基)的少量本征值.要想精确求解大量本征值,传统方法需要加大展开基矢数目,但是这样会显著增加计算量.本文方法可以通过选取平面波波矢的绝对值来计算特定能量区间的本征态.同时选择样条函数能够进一步提高计算精度.

3.3 基组中平面波波矢的值对计算效率的影响

以1 μm 厚度的银纳米板为例,势阱深度大约10 eV,费米能5.5 eV,银纳米板对应在厚度方向大概3800 条能级被占据,如果用以往方法大约需要数万数量的基矢,才可得到比较精确的计算结果.利用本文方法可以极大减小这个数值.例如求解费米面附近的电子时,在势阱里面的区域选择201 个样条函数,势阱外选择60 个,由于平面波基矢用到了正负的k,这样总共的基矢空间为522(为了进一步减小基矢空间,也可以在势阱外不再乘以平面波,也就是只使用样条函数,此时基矢空间为462).通过对角化哈密顿矩阵,得到522 个能量本征值.由于选择的基矢数目非常少,只有能量在 ℏ2k2/(2m) 附近非常有限的能量本征值准确(能够算准的个数大约为1/10 中间样条函数个数).在上述条件下总共需要约190 次这样的计算.于是这种方法就相当于把对大型矩阵的计算,转变为对许多小型矩阵的计算,从而提高计算效率.通过计算能量在 ℏ2k2/(2m) 附近波函数与坐标轴交点个数,可以判断出它们对应于哪个严格解,并且通过对比它们的本征值与严格解,也确认了该挑选方法是准确的.

接下来计算这种方法的相对误差,并分析不同的参数设置对相对误差的影响.势阱不同区域样条函数疏密度的比值对精度有很大影响.由于势阱中间部分势能平缓,原则上讲少数样条函数足以描述;但是在势阱壁势能变化剧烈,需要使用较密集的函数.在基矢总数保持不变的条件下,两端边缘部分与中间部分的样条函数疏密度比率对精度影响很大.图5 为疏密度比率对精度的影响,可以看出r为11.94 时计算精度最高.

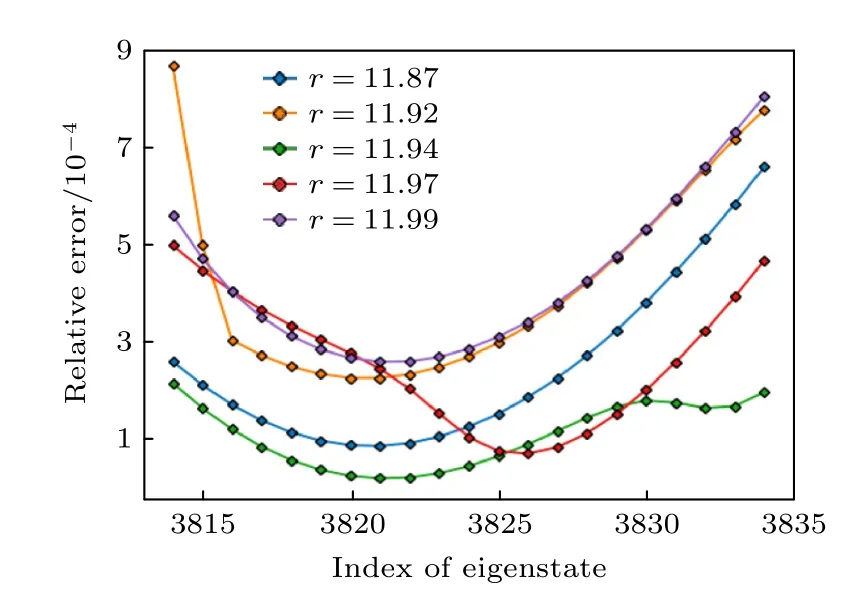
图5 不同的疏密度比率对精度的影响Fig.5.Effect of different degree of closing on precision.

样条函数不同区域与整个函数的宽度比值对计算精度也有一定影响.如(3)式和图1 所示,样条函数包括两边的多项式区域和中间的直线区域,为了计算方便,可以令样条函数的多项式区域,正好与两个样条函数相互交叠的区域完全重合.在图6 中,s为某个样条函数与下一个样条函数相互交叠的部分,与该样条函数间距的比值.可以看到每次计算也就对应着每选取一个波矢,有少数能量本征值(例如图5 中的绿线,大约有中间样条函数个数除10,即20 个)可以被准确地计算.耦合部分与函数间距的比值对计算精度有明显的影响,原则上选择的交叠部分宽度应该比(1)式中的平面波波矢所对应的电子波长小一个量级.至于具体哪个值最优可以通过试探、拟合的方式找到.

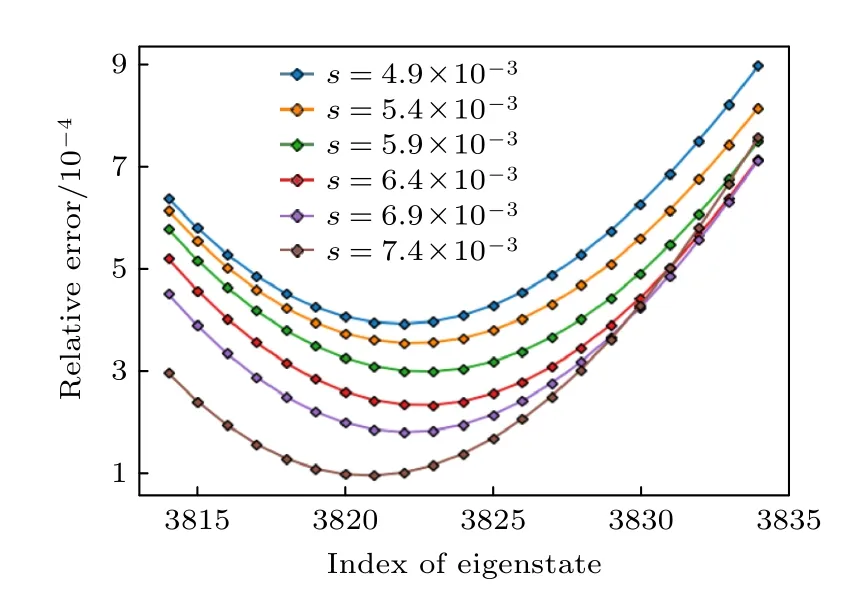
图6 耦合部分与函数宽度的比值对精度的影响Fig.6.Effect of the ratio of coupling part to function width on precision.

对比图5 和图6 可以发现,与3.2 节类似,与耦合部分占函数宽带的比值相比,基矢的疏密度比率是更具决定性影响精度的因素.

最后估算该方法的计算效率相的提升.本文的等离激元数值计算中,最费时的地方一般是哈密顿矩阵的矩阵元与对角化计算.对于矩阵元的计算,需要求解N2个积分.对于矩阵的对角化来说,其计算复杂度为O(N3) .因此基矢总数的减少对计算速度的影响非常大,如果使用通常的平面波基矢对上述系统进行展开,大约需要数万的基矢,则计算量达到了约 1013的量级.而使用本小节的方法矩阵对角化的计算量约为 190×5223,大约在 1010的量级,在保持较好的计算精度的同时,计算效率大大提高.

4 结论

本文利用平面波函数与高斯函数或者样条函数相乘,构建了一种新的基组,并利用格拉姆-施密特正交化方法和Löwdin 正交化方法,对构建的基矢进行正交归一化.通过选择平面波函数中波矢的绝对值,选择性地求解某个能量区间内的本征态,将大型哈密顿矩阵的计算转变为多个小型矩阵的计算,以及通过减少电子势能平缓部分展开基矢数目,极大地加快计算速度.为了方便研究算法精度本文选择一维有限深势阱,发现新的复合基组在保持精度的前提下,可以显著提高计算效率.同时研究了基矢宽度和疏密度比率对精确度的影响,探讨了怎样选择最优的参数.

一维有限深势阱势能在边界跳变,在其他地方为常数,它和金属电势具有类似的变化规律.以纳米金属平板为例,电势在一个费米波矢内从零变化到最小,而后在几个费米波矢内边振荡边衰减到平均值[41].上述计算方法在一维有限深势阱效果很好,因此可以推论该方法能够应用到银纳米板或者其他金属纳米结构等离激元DFT 计算中.给定一个合理的试探性的初始态,利用DFT 理论,通过自洽求解,可以求解系统的基态电子密度分布,之后利用TDDFT 理论求解系统电磁场分布以及光学等性质.