季节冻土区路基土的损伤本构模型研究

李永靖， 程耀辉， 赵涛锋， 陈博文， 马 瑞， 宋 洋

（1. 辽宁工程技术大学 土木工程学院，辽宁 阜新 123000； 2. 辽宁工程技术大学 建筑与交通学院，辽宁 阜新 123000）

0 引言

在我国东北地区年温差较大，路基土随着温度的变化呈现冻融循环现象，属于季节性冻土，易引起东北地区路基在服役期间严重变形，出现冻胀隆起、翻浆冒泥等路基病害，导致土体结构发生改变，路基刚度降低，承载性能变差，而应力-应变关系可有效表征土体的受力变形规律，建立合理的冻融损伤模型对季节性冻土路基结构设计具有指导意义，由此可见，针对冻融循环及围压作用下不同含水率路基土的应力-应变关系及损伤机理进行研究，对季节性冻土路基病害防治具有现实意义［1-3］。

在国内外，人们对冻融条件下路基及路面进行较多的研究，Zhou 等［4］通过冻融、三轴、蠕变以及应力松弛试验发现黄土试件的刚度、黏结参数与冻融循环次数的增加呈负相关趋势。Liu 等［5］对细粒粉砂进行三轴及冻融循环试验发现其应力-应变曲线、破坏强度及弹性模量等力学性能在冻融循环作用下均具有不同程度的影响。Yamamoto 等［6］通过剪切试验研究了人工冻土试样在温度介于-3.0 ℃和-0.3 ℃之间的各种应力路径下的力学行为，并利用声发射从微观角度探索土样内部变形机制。Ismeik等［7］探索冻融循环作用下路基土的工程特性变化，发现冻融循环可导致路基土的无侧限抗压强度降低，而石灰可提高路基土在冻融循环作用下的耐久性。Saberian 等［8］首次探索冻融循环对含有RCA胶粒的路面基层和底基层的工程性能的影响。结果表明，冻融循环次数的增加可导致含有RCA 胶粒的路面基层和底基层的弹性模量升高，无侧限抗压强度降低。Lei 等［9］和Lin 等［10］分析了冻融循环时间、冻结温度、混杂压力等因素对路基土壤累积塑性应变的影响，并建立了可以描述土壤累积塑性应变的数值模型。崔宏环等［11］考虑荷载-冻融耦合作用，基于混凝土损伤本构模型，建立可以描述寒区改良路基土的应力-应变规律。

综上所述，专家学者对路基土的冻融循环特征研究较为成熟，而季节冻土区路基土的损伤本构模型研究较少，且由于季节冻土区路基土的复杂受力特性，所涉及的参数众多，现有的本构模型的使用范围受限。因此本文考虑这一缺陷在前人研究的基础上，引入统计损伤理论，首先对试验路段的路基土选取土样，通过冻融循环试验及三轴压缩试验，探究不同含水率路基土应力-应变曲线随不同冻融次数及围压的变化规律，建立损伤本构模型，分析荷载及冻融循环作用下路基土的损伤特性，从而为季节冻土区路基结构设计及病害防治提供理论参考。

1 试验设计

1.1 原材料

本文以辽宁阜新某公路路基土为研究对象，采用环刀法在路基底部以下约1m 的位置选取土样。根据《公路土工试验规程》的规定，土样均为粉质黏土，其物理性质见表1，其级配曲线见图1。

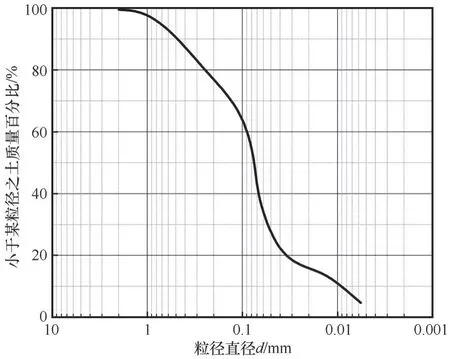
图1 土样的级配曲线Fig. 1 Gradation curves of soil samples

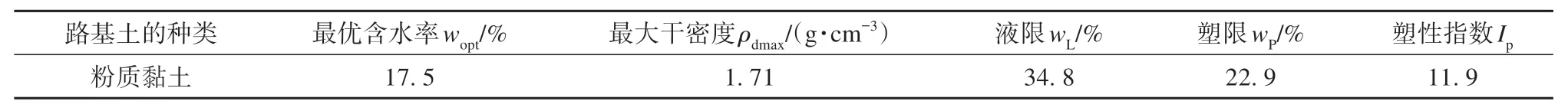
表1 土样的物理性质Table 1 Physical properties of soil sample

1.2 试验方案

依据土工试验规范要求，所取土样需进行烘干，碾碎后用2 mm 筛子进行筛分，将过筛后的土样制备含水率w分别为12.5%、15%、17.5%、20%、22.5%的土样，分三步夯实在模具中，制作5 组φ3.91 cm×8.0 cm的圆柱形试件，每组7个，为防止偶然现象发生，设置三组平行试验，试件脱模后进行养护。

冻融试验仪器：LXSYYQ-40 型号低温试验箱。为防止水分流失，将养护好的试件用塑料薄膜包裹，置于低温试验箱，选取-20 ℃作为试件的冻结温度，20 ℃作为试件的融化温度，24 h 为一次冻融循环：前12 h 进行冻结试验，后12 h 放置室温进行融化，分别进行1、2、3、4、5、6、7次冻融循环试验。

将冻融循环后的试件进行三轴试验，采用GDS非饱和土三轴试验仪器，加载速率选择0.5 mm·min-1，根据现场实际的外部荷载作用在路基土中的附加应力范围为50～300 kPa，因此围压取：100 kPa，200 kPa 及300 kPa，逐渐增加轴向压力，待试件破坏后，停止试验，做好试验记录，并利用体应变与轴向应变及径向应变之间关系计算得到各试件的径向应变。

2 试验结果与分析

2.1 应力-应变关系

冻融循环改变了土体内部结构，影响路基土的力学性能，对其体积变形影响也十分严重［12-13］，这是因为在冻结作用时，试件内部含水率越大，土体冻胀程度越高，对试件内部颗粒间的黏结破坏越大，融化后试件孔隙率也越大，导致试件抗压强度降低，这一现象可通过应力-应变曲线直观表现出来。因三种围压作用下测得的应力-应变曲线呈现的规律相似，以下只针对冻融循环后围压为100 kPa 时的不同含水率试件三轴压缩试验得到的应力-应变曲线进行分析，该应力-应变曲线描述应力σ与ε1是轴向应变及ε3是径向应变的关系，其中径向应变数值为图中数值的绝对值，如图2所示。

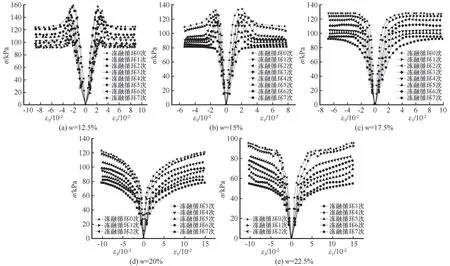
图2 围压为100 kPa时三轴压缩全应力-应变曲线Fig. 2 Total triaxial compression stress-strain curve at 100 kPa confining pressure

由图2 分析可知：含水率为12.5%试件的7 次冻融循环和含水率为15%试件的前6 次（第7 次呈应变硬化特征）冻融循环，应力-应变曲线均出现峰值应力，呈应变软化特征，且随着含水率的增加曲线的应变软化特征逐渐减弱，含水率为12.5%试件的第0 次冻融循环曲线峰值应力为157.41 kPa，冻融循环7 次后曲线峰值应力为99.31 kPa，下降36.91%，含水率为15%试件的第0 次冻融循环曲线峰值应力为133.54 kPa，冻融循环6 次后曲线峰值应力为94.26 kPa，下降29.41%；含水率为17.5%（最优含水率）、20%、22.5%试件的7 次冻融循环，应力-应变曲线均表现为应变硬化，且随着含水率的增加试件曲线的应变硬化特征逐渐明显。相同应变水平下，试件的应力随着冻融循环次数的增加而大幅减小。由上可知，试件含水率小于最优含水率时，随着含水率的降低，曲线的峰值应力增大，且随冻融循环次数的增加而减小，试件含水率大于最优含水率时，随着含水率的增加，曲线没有峰值应力，呈明显的应变硬化特征，这说明最优含水率为季节冻土区路基土试件应力-应变曲线由应变软化转化为应变硬化的界限含水率。

围压可使试件内部土颗粒之间更为紧密的连接，使试件初期强度增大，阻碍试件径向变形，为研究围压对冻融循环作用后土样全应力-应变关系的影响，由以上分析可知，小于最优含水率情况下出现应变软化现象，因此以下只针对含水率为15%试件的试验数据绘制4 组不同围压下冻融循环全应力-应变曲线，如图3所示。

由图3分析可知：冻融循环次数为1次和3次的试件，三种围压下，试件的应力-应变曲线均可见峰值应力，呈现出应变软化特征，冻融循环次数为5次的试件，在围压为100 kPa 时呈现应变软化现象，围压为200 kPa 和300 kPa 时，曲线均呈现应变硬化特征，冻融循环次数为7 次的试件，三种围压下，试件的应力-应变曲线为应变硬化曲线，均没有峰值应力。由以上可知，当试件含水率小于最优含水率时，随冻融循环次数及围压的增大，应力-应变曲线越容易出现应变硬化特征。

3 损伤本构模型研究

3.1 损伤本构模型建立

由于路基土在服役过程中需受荷载及冬季温度的扰动，其颗粒受力状态具有一定的离散性及随机性。当路基土内部出现损伤时，该土体特征由均质性变为非均质性，因此基于统计学原理，在冻融条件下路基土的强度满足随机分布。

假设土体变形为弹性变形，其弹性应变设为εt、此时泊松比为μt，在三向受力状态下，土体在各方向的应变为：

式中：ε1，ε2，ε3为土体各个方向对应的应变。

则土体的体应变εv为：

三轴条件下，三向应力满足σ1>σ2=σ3要求，因此公式（3）可改写为：

设径向弹性应变ε3t和轴向弹性应变ε1t满足下列关系式：

式中：λ为常数，可通过试验测得，仅和应力状态有关。

联立式（4）及式（5）可得：

由Lemaitre有效应力原理［14］可得到应力σi和有效应力σi*之间存在以下关系：

式中：D为损伤变量。

则由广义胡克定律可得［15］，三向受力状态下土体在三个方向上弹性应力与应变之间满足关系式：

式中：E为弹性模量；σ1，σ2，σ3为三向受力状态下土体所受的应力。

根据式（8）能得出：

可推算出试验系数λ满足的等式为：

则土体的体积应变εv为：

联立式（8）及式（11）得：

联立式（6）及式（12）得：

式（13）为考虑土体的体积变形而改进的损伤模型。

由于路基土在服役过程中受到冻融循环及上部荷载双重作用，因此损伤变量D表示为：

式中：Dl为荷载作用下的损伤变量；Df为冻融循环作用下的损伤变量。

而Df可通过冻融循环前后弹性模量所表示，即：

式中：E0、En分别为初始弹性模量及n次冻融循环后的弹性模量。

在1939 年，科学家Weibull 基于“最弱环假设”提出了可以精确描述出材料内部的损伤分布、材料受损后的损伤演化规律的材料破坏强度理论，即为Weibull分布函数。自该函数提出以来，已被国内外专家学者广泛应用于分析土体的强度等参数，进一步证明Weibull 分布函数与土体损伤之间的相关性［16-18］。因此本文假设路基土是由强度不同的微元体所组成。荷载条件下，土体的损伤规律满足Weibull 分布［19］，且根据Kachanov 对土体损伤的定义可知Dl的计算公式［20］：

从微观视角来讲，当作用在土体上的外荷载强度达到屈服强度F时，出现于土体内部的微元损伤数量达到Nf

［21］，即：

式中：f（x）为Weibull 分布函数的概率密度函数［22］，其满足的关系式为：

式中：m，F0为对数分布参数。

因此Dl满足的关系式为：

联立式（19）、式（15）及式（14），可以得出土样在冻融与荷载作用下的损伤变量D为：

式中：F为土体内部微元强度随机分布量，满足的关系式为：

式中：φ为土体内摩擦角，可由摩尔库伦准则计算得到。

联立式（13）及式（20）可以得到有围压土体在弹性应变条件下的损伤本构方程为：

3.2 模型分布参数确定

损伤本构方程式（22）中参数En可由三轴试验得到，轴向应力、泊松比及围压包含在参数λ中。而分布参数m及F0则由不同条件下试件应力-应变曲线上的特殊点间的关系确定，如图4所示。

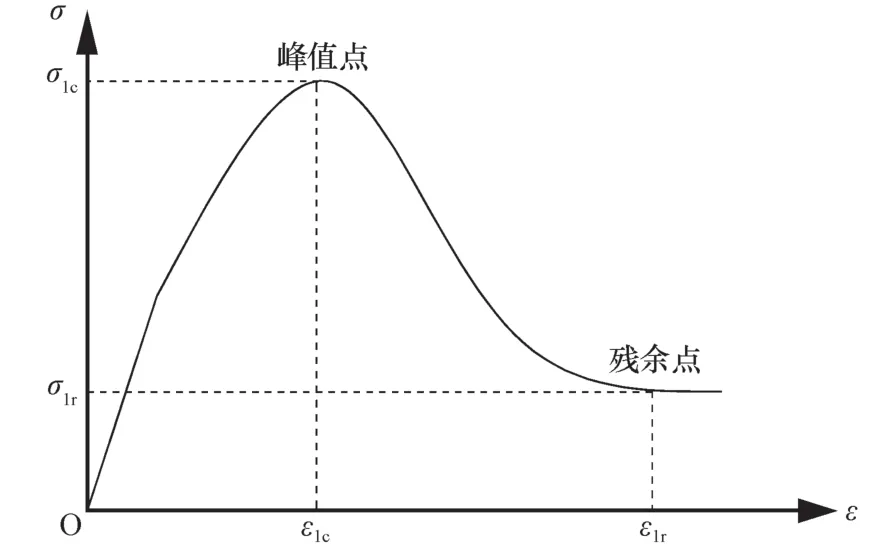
图4 应力-应变曲线Fig. 4 Stress and strain curves

在土体峰值应力位置存在以下几何关系：①ε1=ε1c时，σ1=σ1c；②ε1=ε1c时，dσ/dε=0。

将几何关系（1），带入式（22）可得：

结合几何关系（2）与式（21）、（23）可得：

联立式（21）、（22）、（24）可得分布参数m及F0所满足公式：

式中：F1c、D1c分别为季节冻土区路基土的峰值强度、应力-应变曲线峰值处的损伤变量，二者满足以下关系：

σ1c、ε1c为根据围压变化的量。

3.3 模型与试验结果验证

为验证所建损伤本构模型的合理性及准确性，现根据表2数据绘制对应应力-应变曲线图，并与试验数据进行对比，其中分布参数中所涉及的土样内摩擦角φ采用不同围压作用下的莫尔应力圆计算获取，为三组平行试验的平均值，计算结果为18.03°，如图5所示。

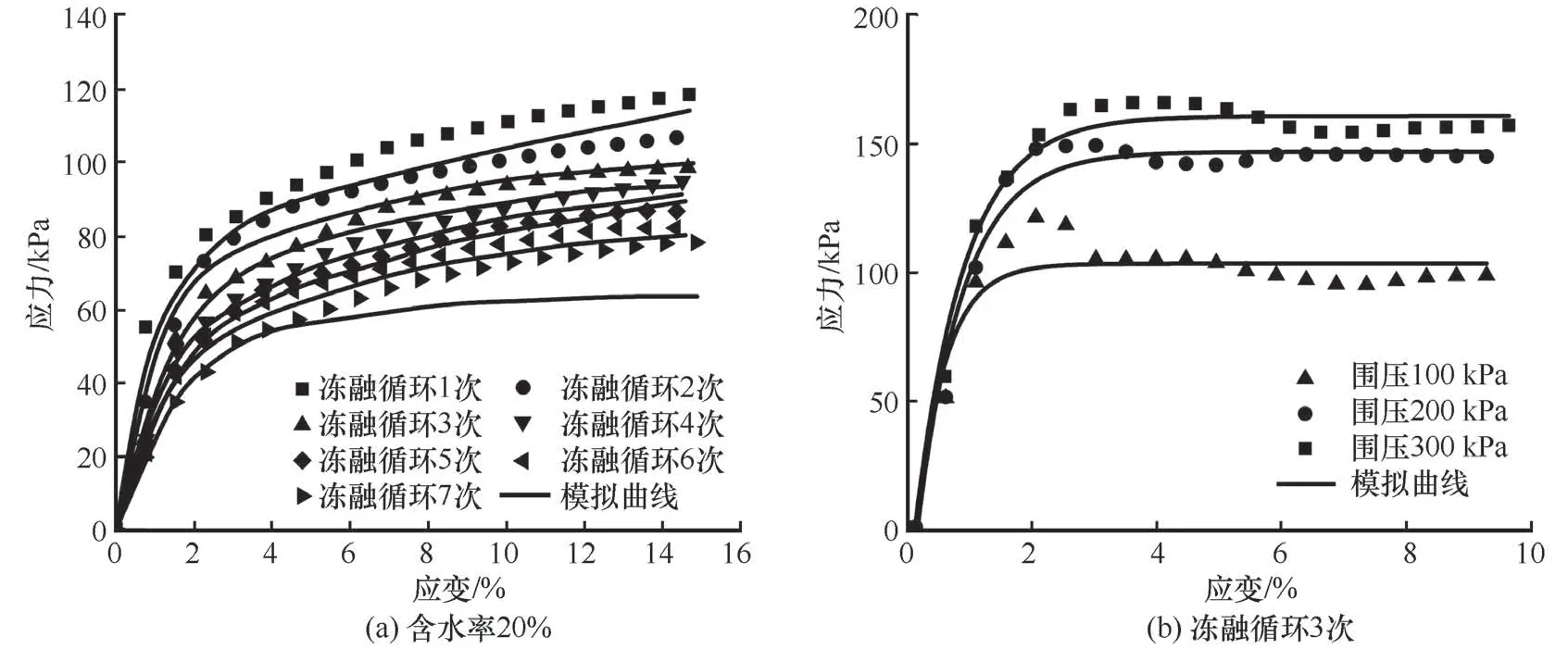
图5 模型曲线和试验曲线对比Fig. 5 Comparison of model curve and test curve

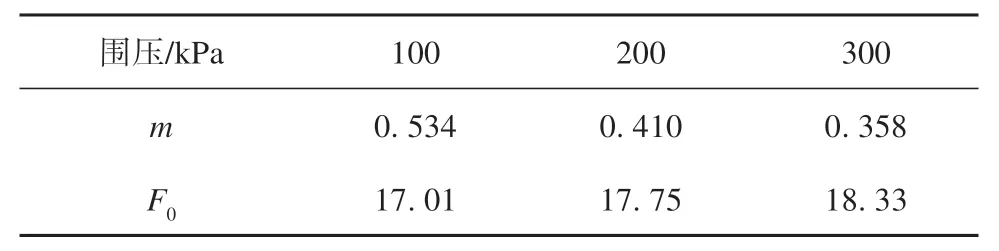
表2 参数计算值Table 2 Parameter value

由图5 分析可知，模型曲线与试验曲线吻合度较好，两曲线所呈现的变化规律基本相同，均表现为先快速增长后平稳的趋势，说明所建立的损伤本构模型能够将季节冻土区路基土的应力应变特性较为准确地反映出来，为研究东北地区季节冻土区路基土的冻融损伤特性提供了理论依据。

4 结论

（1）试验结果表明，季节冻土区路基土的最优含水率为其应力-应变曲线由应变软化转化为应变硬化的界限含水率，当含水率小于最优含水率时，随着含水率的降低，曲线的峰值应力增大，且随冻融循环次数的增加而减小，当试件含水率大于最优含水率时，随着含水率的增加，曲线没有峰值应力，呈明显的应变硬化特征。

（2）实验分析表明，随冻融循环次数及围压的增大，季节冻土区路基土的应力-应变曲线越容易出现应变硬化特征，说明影响季节冻土区路基土内部结构变化的主要原因为冻融循环，而周围土体压力可以起到抑制其内部结构破坏的作用。

（3）基于Lemaitre 有效应力原理，结合Weibull分布建立了季节冻土区路基土损伤本构模型，与试验曲线吻合度较好，可反映出季节冻土区路基土的应力-应变曲线呈先增长后趋于平稳的变化规律，说明所建模型能够较好地描述季节冻土区路基土的应力-应变关系。