油田站库PID 控制器参数鲁棒整定及其应用
2023-10-05宋伟强大庆油田有限责任公司第四采油厂
宋伟强(大庆油田有限责任公司第四采油厂)
油田的转油站和联合站等站库应用变频器控制调节外输泵实现外输,游离水脱除器通过控制气动阀调节实现自动放水,这些变频器和气动阀等均采用PID 控制器进行控制。PID 控制算法中比例、积分、微分参数设定直接影响PID 控制性能[1-3]。
PID 控制器的参数整定,无论是在理论上还是在工程实现上方法都很多。近年来,PID 参数整定方法更是融合了许多新的特性,大体上有参数辨识法[1]、频域指标法[2]、鲁棒整定法[3-4]、最小可达方差整定法[5-6]、内模法[7-8]、参考模型法[9]和智能搜索法[10-11]等参数整定法。这些算法都为PID 参数整定提供了丰富的选择。然而,单一目标的PID 参数整定常常得不到期望的结果。这是因为有多个PID 参数可以满足单一目标,故在实际应用中更加关注的是多目标融合的PID 参数整定方法[12]。
目前油田站库在用PID 参数整定主要以经验试凑法为主,一般由系统开发人员根据经验设置,虽能满足基本生产控制需求,但实际生产过程中存在节能效果不佳、变频器和气动阀振荡运行、液位和界面波动大等情况。根据现场实际情况,开展研究油田站库PID 参数鲁棒整定技术,通过采集输入、输出及控制参数等数据,建立数据驱动的鲁棒模型,之后实施鲁棒模型下的多目标融合的鲁棒PID参数整定。
1 鲁棒建模
1.1 模型结构及模型阶次
通常,实际对象的模型结构均可描述成如下的输入输出结构见式(1):
式中:θi和βi为待辨识的参数;ε为自噪音;x和y分别是过程的输入和输出信号,为避免不同量纲引起的建模误差,通常建模采用的数据为无量纲的标准化数据。在方程中,有两个参数即所谓的模型阶次m,n需要事先确定。通常采用赤池信息准则(AIC)或贝叶斯信息准则(BIC)来确定。
转油站和联合站的结构类似,系统基本结构见图1。实际建模显然可以建立设定值和液位之间的闭环模型,也可以建立变频器到液位之间的开环模型。虽然可以通过机理的方式来确定模型,但输油泵含有非线性环节且需要考虑老化问题,直接利用机理模型困难较大且不一定满足现场实际情况,为此采用数据驱动方式建模。

图1 系统基本结构Fig.1 Basic structure of the system
现场采集的数据包括液位设定值,变频器频率和实际液位值,设定值、频率和液位的变化曲线见图2。从采集的数据看,现场的数据波动较大,与常规的工业过程平稳监控数据差异较大。直接利用这些数据按最小方差准则来建模可能得不到期望结果。为此,从鲁棒建模的角度出发,建立具有一定鲁棒性的模型。

图2 设定值、频率和液位的变化曲线Fig.2 Change curve of set value,frequency and level
建模之前需确定模型的结构。在模型确定阶次时,只需要关注系统基本结构模型,即建立变频器的频率和液位之间的模型。在确定模型阶次之前,还需确定系统是否存在滞后环节,为此对有关数据进行相关分析,相关系数分析结果见图3。由图3可确定变频器频率和液位之间有滞后存在(对于该采样数据,滞后为一个采样周期时相关度最大)。另一方面,被控对象和泵大多是在线性区间工作,因此可假定系统的模型结构为G(s)e-τs形 式,其 中G(s)为线性部分的传递函数,e-τs为滞后环节的传递函数。

图3 相关系数分析结果Fig.3 Results of correlation coefficient analysis
对于有滞后环节的系统,在确定阶次时需要首先给定滞后时间常数。对于该样本采用最小二乘法简单辨识,模型拟合残差(%)与参数个数关系见图4。在图4 中,蓝色框是AIC 准则给出的最优模型参数个数,红色是基于所给数据能获得的最佳拟合效果的参数个数。但AIC 准则给出模型参数个数达21 个,此时它对应一个高阶模型。高阶模型无论是在控制器设计,还是在系统性能分析中,都不是一件简单的事。实际上,模型参数为3 个时AIC准则的值与21 个时对应的AIC 值相差很小。结合图4 的框图看,被控对象为储油罐,它与一阶惯性环节近似,泵在线性区间工作时也可由一阶惯性环节描述,因此,图4 中黄色框内的模型用二阶系统描述就可满足大部分需求。模型阶次和拟合曲线见图5。图5 给出了AIC 推荐的模型和选定的模型的拟合曲线,虽然AIC 模型在一定程度上更好地匹配了数据变化趋势,但该结果仅仅是从数据拟合的角度来考虑,建立的模型是否符合实际并没有考虑。另一方面,选定的结构虽然没有AIC 准则高,但其拟合曲线也能很好地匹配设定值的阶跃变化趋势。
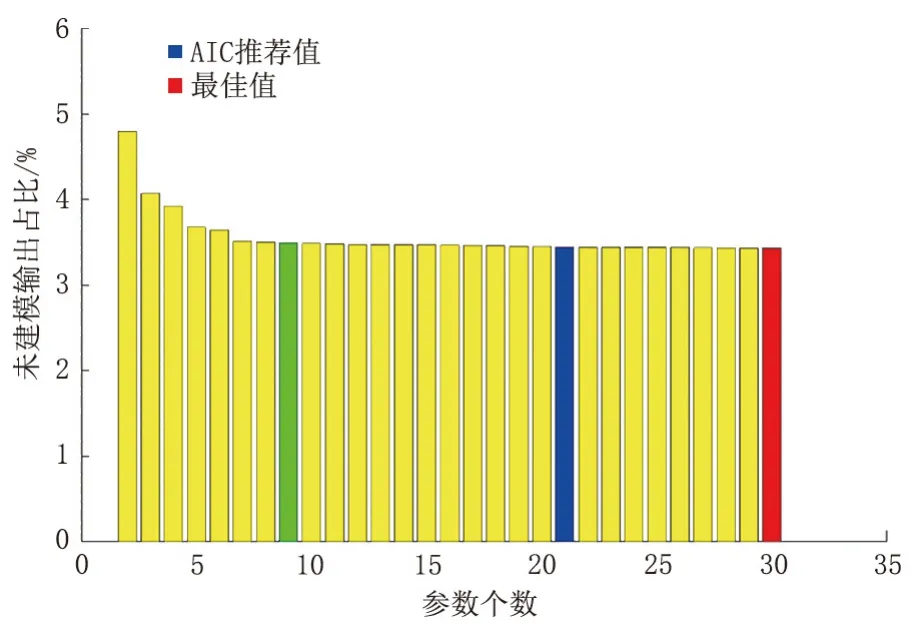
图4 模型拟合残差(%)与参数个数关系Fig.4 The relationship between fit residuals(%)and the number of parameters

图5 模型阶次和拟合曲线Fig.5 Model order and fitting curve
尽管AIC 准则给出的推荐值与选定值有一定距离,但图4 给出的结果就给出的数据选用2 阶模型来说,带来的风险和AIC 准则的最优值差异不是很大。另一方面,选定的结构模型结构简单,便于后续分析。因此,综合考虑,在接下来的分析中,将采用2 阶滞后模型结构作为最优的模型结构。
1.2 数据驱动鲁棒建模研究
目前优化目标有多种方法可实现数据驱动建模。比如在数据预处理按格拉布斯准则剔除异常数值后利用最小二乘法实现数据驱动建模;也可以不剔除异常值,直接利用最小一乘实现数据驱动鲁棒建模。由于现场数据波动较大,很难区分异常值与正常值,故对异常值敏感的最小二乘法不能满足现场实际需求。为了提升模型的鲁棒性同时保全样本,在建模优化目标中优先选用了具有对异常值不敏感的最小一乘法。
最小一乘法只要求各实测点到回归直线的纵向距离的绝对值之和为最小。它不要求随机误差服从正态分布,“稳健性”比最小二乘法好。在数据随机误差不服从正态分布时,此法的统计性能优于最小二乘法。最小二乘法的目标函数是:
式中:yi(i=1,2,…,N)是实际系统第i为;为yi的估计值。最小二乘回归直线是一条均值直线,最小二乘回归也可称为均值回归。最小一乘法的目标函数是:
最小一乘回归直线是一条中位数直线,因此最小一乘回归也可称为中位数回归。
在建模中面临的问题实际上是一个多元回归问题。可抽象描述为对p个自变量x1,…,xp和因变量y进行N 次观察(即N 次采样),得观察数据,记为x1(i),…,xp(i),y(i),一般要求N>p,满足下列线性关系:
最小一乘线性回归须使目标函数最小。对于此项目来说,实际面临的回归问题是一个自回归问题,见式(5):
由上一节的模型结构可确定式中的m和n,通过最小一乘回归即可辨识θ和β,进而可获得相应的数据驱动模型。
2 控制回路参数鲁棒整定
基于PID 控制器的动态性能和鲁棒性能的实际需求,采用内模控制(IMC)和绝对累计误差(ISE)相融合的方法来整定PID 参数,在保障控制的动态性能的前提下,实现整定好的控制器具有一定的抗干扰性。内模控制是一种基于过程数据模型的控制策略,其结构是将被控对象系统与过程模型并联,取系统输出与模型输出的偏差作为反馈。虽然不同的IMC-PID 略有差异,但总体类似。IMC 控制结构及等效形式见图6。
稍加推导可得常规PID 反馈控制器与IMC 的关系见式(6):
第一步:对对象模型进行分解,分解为两部分见式(8)
式中:f(s)为低通滤波器;λ为低通滤波器的设计参数;i为滤波器的阶次,与的阶次密切相关。与常规IMC-PID 不同,为满足PID 控制器的动态性能,λ满足式(12)要求。
式中:e(t)为设定值与输出值的偏差。该目标函数的目的是在给定的滤波器结构下,寻求合适的参数λ使得对应的控制器作用下的系统的绝对误差累积极小化。
3 现场应用
基于上述算法,采用C#开发了IMC-PID 软件包。为验证PID 参数整定软件的适应性,采集了某转油站的阶跃信号,该站初始PID 参数为Kc=50,Ki=2.5 s-1,需要注意的是该站的积分增益Ki和积分时间Ti的关系是Ki=1/Ti。利用该阶跃信号和PID 参数进行闭环辨识。选择模型结构选为零极点结构。相应的参数辨识为a=3.241,b=3.911×10-7,c=0.007 64;d=3.545 s,系统辨识曲线见图7。

图7 系统辨识曲线Fig.7 System identification curves
图7 中的阀位输出值是软件模拟的阀门开度变化曲线。采用模型IMC-PID 法进行参数整定,PID参数整定得Kc=87.8576;Ti=0.198s(Ki约等于5s-1)。
该转油站整定后连续2 d 采集液位信号,液位设定值为2.2 m,系统能够稳定控制,正常时液位波动值在±3 cm 以内,在来液有波动或干扰情况下,系统能够快速达到设定值,恢复稳定控制。
参数整定15 d 后,对整定前后能耗作了对比评估。评估结果表明整定前吨液耗电0.289 8 kWh,整定后吨液耗电0.259 0 kWh,整定后平均节电约为10.6%,从耗电量和液位控制看,整个系统运行稳定,耗电量等关键指标优于预期指标。整定前后能耗对比见图8。

图8 整定前后能耗对比Fig.8 Comparison of energy consumption before and after tuning
4 结论
针对油田转油站和联合站的变频器以及游离水脱除器的气动阀等关联控制器的实际情况,构建了基于鲁棒模型的多目标融合的PID 参数整定架构。首先采用相关分析法和AIC 信息准则确定了模型结构中的滞后环节和模型阶次,并根据现场实际情形确定了将转油站的模型结构选择为二阶滞后模型结构;接着针对油田站库的控制回路输出波动大采用了最小一乘法来建立具有一定鲁棒性的模型。在此基础上,利用内模控制法实现了PID 参数整定,特别地,在滤波器的参数选择上采用了误差绝对值累积极小化技术。在某转油站开展现场应用表明,利用采集的阶跃信号通过软件平台整定的PID 控制器参数能够满足现场控制要求,整定后平均节电约为10.6%,优于预期目标。
