基于大数据分析的电力用户综合能效评估模型
2023-10-05马秋波朱廷俊夏成璧朱李铀潘艳青
马秋波,朱廷俊,夏成璧,朱李铀,潘艳青
(国网甘肃省电力公司庆阳供电公司,甘肃庆阳 745000)
建立健全的电力用户能效评估指标体系,是提升该领域用户能源利用率的首要环节[1-9]。在配电侧降低线路损耗、用户侧降低设备损耗是提高企业电能利用率的基本准则。随着大数据技术的推广,电力用户的各种用电行为早已“有迹可循”,这些痕迹为调研不同行业的电力用户提供了技术支持[10-12]。在科学的评价指标体系引导下,电力用户能及时改进经营策略,而电力公司可有效降低线路损耗,从而达到配用电的双赢。在此背景下,该文从实用性、科学性与可观测性的角度出发,对电力用户在综合能效评估时所使用的大数据分析及存储方法进行了研究。基于多维矩阵的大数据分析技术对电力用户的观测值加以扩展,并使用熵值评估法(Entropy Method)避免了评估过程中的主观因素影响,再利用最小二乘法(Generalized Least Squares,GLS)进行算法集成,进而提升了评估的精度。
1 理论基础
1.1 大数据分析技术
在对电力用户进行能效评估时,随着企业数据采集密度的增长,各种状态数据通常采用时间序列的形式在服务器上加以存储。记x为电力设备某个指标在复数空间上的T维时间序列,则N个序列可以构成如式(1)所示的观测矩阵:
式中,C为复数空间。当N远小于T时,可将xi继续拆分,并叠加得到更高维度的X′:
对电力用户按照指标体系进行数据采集后,再对各个指标下的数据加以采集,随后便能建立状态量数据集的高维矩阵,最终通过大数据模型即可实现对能效的评估。数据采集后,首先需量化所采集的状态量与能效评估间的相关性。因此,该文引入了置信度指标A来进行相关性的度量:
其中,P是事件发生的概率,σ是方差,Li,j表示状态量i在j条件下出现异常,Mi是状态量在观测值中出现异常。随后,借助ARMA 模型(Auto-Regressive and Moving Average Model)研究高维矩阵的样本协方差矩阵并实现数据挖掘[13-15],以获得该矩阵的谱分布,从而得到电力用户的异常能效指标。ARMA 是基于自回归(Autoregressive Model,AR)与滑动平均(Moving Average,MA)的复合模型。对于记录了某个指标在n个状态的高维矩阵X′=(x1,x2,…,xn),其时间序列xt的功率谱密度计算方法如下:
首先将高维矩阵转化为以p、q为模型参数的ARMA(p|q)过程,且记B为延迟算子,ϕ、θ为比例因子,则有:
其中,εt是基函数,a和b为展开阶数。
此时,记Φ为序列经傅里叶变换后的功率谱密度,则其计算方法为:
其中,ω为傅里叶变换中的角频率。
当a、b均为1时,即可得到该文使用的ARMA(1,1)模型。对于该模型,可根据式(6)得到功率谱密度的计算方式为:
其中,φ是[-1,1]的常数。对于采样矩阵X,其协方差矩阵的计算方法如下:
对Sn进行p个时刻的采样,并计算Sn的能量谱密度(Energy Spectrum Density,ESD),其计算方式为:
其中,I是采样点中出现异常数据的概率。接着对式(7)进行斯蒂尔切斯变换,即可得到极限谱密度函数,此处仍以ARMA(1,1)模型为例,有:
1.2 大数据评估方法
在对样本数据进行检测后,还需确定评价指标的权重值。由于电力用户的指标体系较为复杂,故该文采用基于最小二乘原理的熵值评估法确定各级指标的权重。
信息熵(Information Entropy)是信息理论中评价空间内部信息分布无序程度的评价指标,信息的无序程度越短,其携带的信息量便越大。在大数据评估中,通过指标观测值提供的信息量大小可确定该指标的权重,这便是熵值评估法的基本思想。
对于电力用户在m个评估项目,n个评价指标下,能够得到观测数据矩阵R=(rij)m×n,其可表示为:
对于第j个指标,其权重uj的计算方法如下:
在实际的能效评估时,由熵值评估法取得的权重为客观权重uj。由于在现有的评价体系下,存在固有的主观评价权重wj,故需尽可能降低两套权重间的偏差。为此,该文引入最小二乘法进行综合集成,记最终的综合权重为W=(W1,W2,…,Wm),则优化的目标函数H为:
由于两种权重赋值方法所得到的权重是离散分布的,因此引入对熵h(u1,u2),并将该问题转化为数学规划问题,记d为集合权重:
根据最小二乘法,该数学规划模型的最优解如下:
此时,可得到综合赋权后的客观权重a1与主观权重a2:
2 方法实现
2.1 大数据存储与读取结构实现
该文基于某地区200 家重要电力客户数据集进行模型的验证,由于数据量大,为提升数据的运算分析效率,需基于指标评价体系对数据的存储体系加以设计[16]。该文的指标体系共分为三级,其中,一级指标体系包括技术能效A1、经济能效A2、管理能效A3。图1 给出了技术能效A1的部分指标。

图1 文中设计的部分指标体系
由于该文使用的原始数据均按照各个指标存储于389 213 个小文件中,而传统的HDFS(Hadoop Distributed File System)更适合于大文件的流式存储,故该文使用图2 所示的策略对存储方式进行优化。
图2 中设计了小文件合并的数据接口,归并后的大文件元数据结构如表1 所示。

图2 小文件优化存储策略
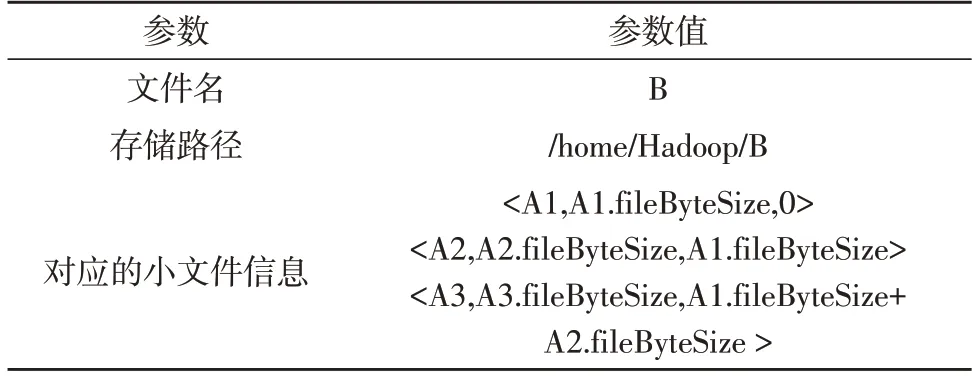
表1 归并后大文件的元数据结构
在经历前期的数据采集后,依据该指标体系与高维矩阵分析方法,得到了不同指标观测值的扩展序列。然后再使用并行化的HDFS 大数据处理技术按照指标体系进行数据存储,且采用1 个Master 和7个Slave 存储节点,单个Master、Slave 节点的配置均如表2 所示。测试结果表明,相较于传统的单服务器存储,数据的访问效率提升了64.5%。

表2 Master与Slave节点的配置
2.2 工程实现
随后通过读取HDFS 文件系统上的观测数据,确定评估模型的各项指标。在确定指标体系中一、二级指标的权重时,采用最小二乘法集成赋权,各个指标的权重值计算结果如表3 所示。
从表中可以看出,在进行电力用户的能效评估时,在该文的评估模型下,用户的技术指标对用户影响较大,权重为57.13%。而用户的管理效能对用电能效的影响则较小,权重仅为10.93%。在三级指标的权重赋值中,由于各指标下的观测值已采用高维矩阵进行了序列扩展,故可直接使用熵值评估法进行权重赋值。以B8下的三级指标C16-C21为例,各个指标的熵值、差异系数及熵权重的计算结果如表4所示。

表3 一二级指标权重值
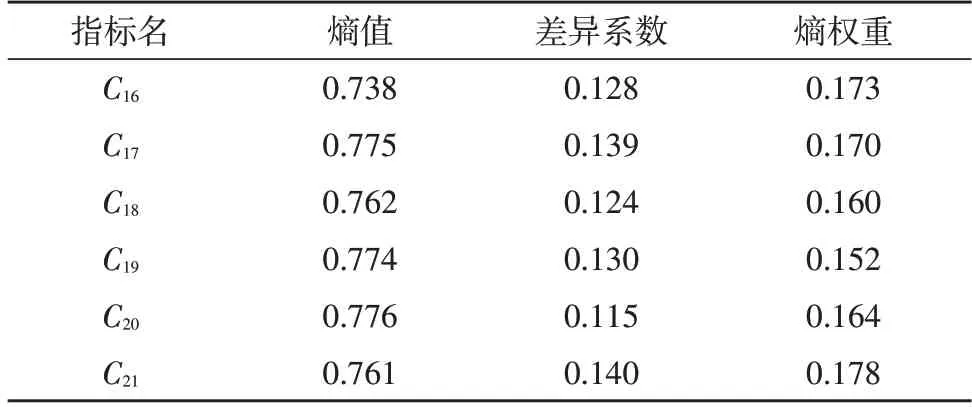
表4 B8下各指标权重计算结果
表5 给出了200 家电力用户在技术、经济与管理这3 个一级指标下的评价结果。
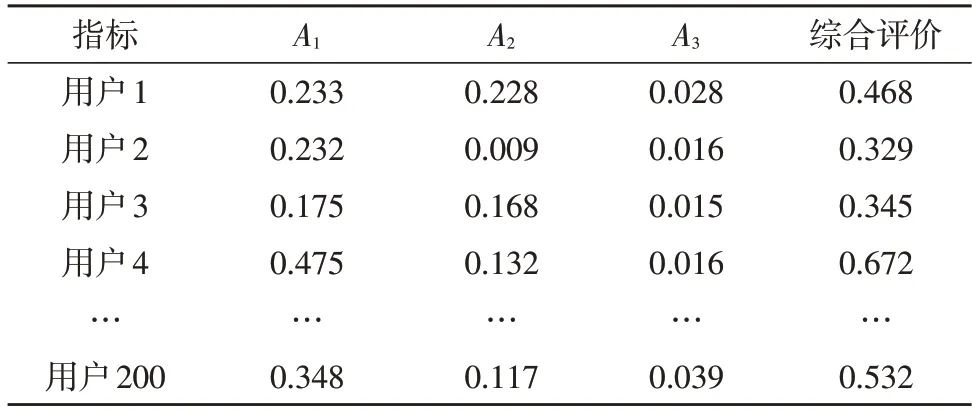
表5 企业能效评估结果
以表中所显示的5 家用户为例,通过综合评价其能效水平依次排序为用户4>用户200>用户1>用户3>用户2。通过综合性的能效评估,各用户均能够评估自身在能效上的弱势项,并针对该项进行专项提升,从而更优地提升生产效率。
3 结束语
该文引入了大数据分析方法进行电力用户的综合能效评估,基于HDFS 大数据存储结构建立了完备的评价指标体系。在数据处理上,基于ARMA方法建立了观测样本的协方差矩阵,在确认评估模型的三级指标时,使用了信息熵理论中的熵值评估法,有效避免了评价过程中的主观因素影响。计算样例证明,该方法能够通过打分的形式有效评估用户的当前能效水平,并可为能效的提升给出合理的改进方向。
