基于TSNS-RAE的多模态过程故障检测

郭小萍，李志远，李 元

(沈阳化工大学 信息工程学院，沈阳 110142)

0 引言

随着现代工业过程生产规模的不断扩大以及生产过程复杂性的不断提高，为了保证整个生产过程的安全性和可靠性，及时有效的故障检测变得越发的重要，对其的研究也具有重大意义[1-2]。

现代工业生产过程大多是多模态的工业过程。多模态工业过程同时还具有动态性和非线性的特征。因此相较于普通单模态过程，多模态过程的监控要更加复杂。芯片制造过程[3]，青霉素发酵过程[4]和半导体生产过程[5]是最常见的多模态工业过程。

复杂多模态过程的监控，可以从数据标准化方法和故障检测方法两个方面进行研究。

多模态过程的一种监控策略是选择合适的数据标准化方法。目前最常用的数据标准化方法是Z-Score标准化方法，但是该方法并不适用于多模态过程。局部近邻标准化(NS)的数据处理方法[6-7]的提出有效的解决了Z-Score不能处理多模态数据的缺陷，NS方法虽然可以将多模态数据合并成单模态，但是忽略了样本的时序相关性，在处理动态过程时检测效果不佳。为了进一步完善NS在处理动态性生产过程的不足，冯等提出了时空近邻标准化的数据处理方法[8]，该标准化方法不仅将多模态数据融合为单模态数据，同时还能消除前后数据之间的动态相关性，进而将故障数据与正常数据更好的分离开，达到更好的故障检测效果。

多模态过程的另一种监控策略是选择合适的故障检测方法，主成分分析(PCA)[9]、偏最小二乘方法(PLS)[10]和独立成分分析(ICA)[11]是最常用的故障检测方法。这些方法都是基于数据驱动的传统故障检测方法。它们都是线性学习的降维方法，在处理非线性数据时效果不佳。

近年来，深度学习方法在图像分类、目标检测、自动驾驶等领域都有着深入的研究。相对于传统的基于数据驱动的方法，深度学习模型可以提取多变量数据更深层次的数据特征，表现出强劲的处理各种非线性信息的能力[12]。常见的深度学习方法有卷积神经网络[13]，循环神经网络[14]，自动编码器[15]。其中自编码器的应用更为广泛。目前常用的自编码器模型有堆叠自编码器(DAE)，鲁棒自编码器(RAE)，正交自编码器(QAE)，变分自编码器(VAE)。

本文选择时空近邻标准化方法(TSNS)为数据的标准化方法，选择鲁棒自编码器(RAE)模型为故障的检测方法，将两种方法进行结合，提出基于TSNS-RAE的故障检测方法来对多模态工业生产过程进行故障检测。

1 数据的预处理

1.1 标准差标准化(Z-Score)

在进行故障检测之前，需要对采集的数据集进行预处理。针对工业过程的特点选择最合适的预处理方法来对数据进行标准化，对之后的故障检测有着十分重要的意义。

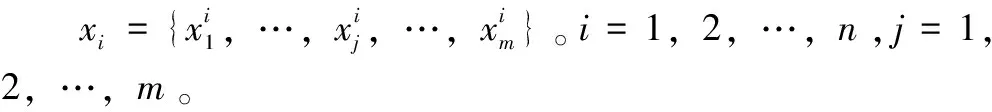
(1)

(2)

(3)

Z-score 标准化使样本集的每个特征具有均值为 0 标准差为 1的特点，消除了数据量纲的影响，使不同变量的方差(离散程度)相同。普通的Z-Score标准化方法在处理多模态数据时，无法将多模态数据转换成单模态数据，导致检测效果不佳。

1.2 邻域标准化(NS)

为改善Z-Score方法处理多模态数据时的不足。Ma等提出了邻域标准化方法(NS，neighborhood standardized)，该方法使用最近邻样本的近邻集标准化当前样本，NS的步骤如下：首先寻找样本x的最近邻样本x1，其次寻找x1的前N近邻样本集，计算此近邻集的均值m(N(x(1)))和标准差s(N(x(1)))，最后使用式(4)对x进行标准化：

(4)

邻域标准化方法(NS)虽然可以将多模态数据转换成单模态数据，但是该方法只考虑了空间上的近邻信息，忽略了时间上的近邻信息。所以NS在处理动态过程的工业数据时，往往忽略了数据的动态性，无法消除之前时刻样本对后面时刻样本的影响。无法保证所用的近邻样本应来自于样本的相近时刻。

1.3 时空近邻标准化(TSNS)

为了进一步改善NS方法的不足，冯等提出了TSNS方法。TSNS的步骤如下：首先在训练集中寻找样本x在时间方向上的前N近邻样本集N(x)= {x1(x)，…，xt(x)，…，xN(x)}，再寻找xt(x)在空间方向上的前K近邻样本集N(xt(x))={x1(xt)，…，xf(xt)，…，xK(xt)}，使用式(5)和(6)计算此样本集的均值m(N(xt(x)))和标准差s(N(xt(x)))，最后 使用式(7)将x进行标准化处理得到标准化之后的样本。

(5)

(6)

(7)

TSNS方法对数据进行标准化时不仅单纯使用空间近邻信息，还充分考虑时间序列信息的影响，使用来自于相近时刻的样本近邻集。经过TSNS处理之后的样本在消除数据多模态的同时也消除了动态性，能够实现故障与正常样本在空间上的分离。为之后对过程数据进行故障检测奠定基础。

2 基于鲁棒自编码器(RAE)的故障检测

2.1 普通自编码器(AE)原理

普通的自动编码器(AE)是一种常用的降维神经网络，经常用于数据的降维和特征提取。它分为编码器和解码器两部分，其结构如图1所示。在对原始数据进行数据降维处理和特征提取时，需保持输出层数据维数与输入层输入维数相同，而中间隐藏层数据维数则可以根据实际情况而设定。

图1 自编码器网络结构示意图

自编码器由编码和解码两步构成，输入层原始数据经过编码过程进行降维处理，在隐藏层得到数据的特征，然后对隐藏层特征进行解码在输出层得到原始数据的重构。自编码器模型结构如下式：

hi=f(W1xi+b1)

(8)

(9)

式中，i=1，2，3···，I是采样时间，xi∈RJ×1是第i个样本，hi∈RK×1是原始输入xi的特征。W1∈Rk×J和b1∈RK×1是输入层到隐藏层之间的投影权重和偏置。r(xi)∈RJ×1是对提取特征hi的解码或者说是对输入数据xi的重构。W2∈RJ×K和b2∈RJ×1是隐藏层到输出层的投影权重和偏置。

公式(8)和(9)中f(i)，g(i)是隐藏层和输出层的激活函数，根据实际工业生产过程的特点，激活函数的选择如下：

(10)

g(x)=x

(11)

一个好的自编码器模型在提取数据特征时，应保持输出端重构数据r(x)与输入端原始数据X的差异尽可能的小。这个差异就叫作损失函数就是我们需要最小化的目标函数。普通自编码器的目标函数如下：

(12)

式中，xi是第i个样本数据点，r(xi)是第i个样本的重构值。通过累积贡献率方法选择好好隐藏层的节点数K，设置好训练次数之后，可以选择Adam优化算法来对编码器模型进行训练，当损失函数值慢慢下降并最后收敛趋于稳定之后，编码器的训练阶段完成。得到最小化的损失函数和自编码器模型参数值。我们可以将此训练好的编码器用于之后的故障检测之中。

自编码器通过提取数据的深层特征来表示原始的过程数据。自编码器模型训练的效果与模型复杂度和待训练的数据集的质量有着密切的联系。当训练集数据量较少或训练集包含噪声的时候，训练出来的模型容易出现过拟合现象，即测试集数据在模型上的表现效果远差于训练集在模型上的表现效果。为了提高训练数据集质量，在训练之前需要把正常数据与噪声隔离开。但是单纯的把噪声和冗余从训练集数据中剔除是十分困难的做法。

2.2 鲁棒自编码器(RAE)原理

为了避免编码器因为训练数据量较少或噪声干扰在模型训练时出现的过拟合情况，对普通的自编码器(AE)进行改造，提出鲁棒自编码器(RAE)的概念。

鲁棒自编码器相对比于普通编码器，能够将被噪声污染的原始数据进行编码解码并且很好的提取数据特征和输出原始数据的重构。这样的编码器更有利于处理复杂多变的过程数据。

因此在训练模型之前可以人为的给训练集加上高斯噪声，达成对数据的损坏，编码器如果可以从人为损坏的训练数据集提取出数据特征，并且重构出原始数据，那么这个编码器就便具有识别噪声的能力，具有抗噪性，有更好的鲁棒性，从而提高模型的泛化能力。

RAE就是通过对输入数据进行一定程度的损坏，通过训练来将其还原为原始数据空间来学习数据中关键特征的自编码器。

RAE模型的示意图如图2所示，和普通自编码器有着相似的结构[17]。

图2 鲁棒自编码器示意图

RAE与普通AE的区别就是训练阶段时在原始数据基础上人为加入高斯噪声ε，用加入噪声之后的数据来作为模型输入数据，而模型的训练目标依旧是未加入噪声的原始数据，鲁棒自编码器的目标函数如式(13)：

(13)

在理想情况下，公式(13)可以被等效成一个加了正则化项的自编码器：

(14)

RAE模型的训练过程与AE类似。分别选择sigmod函数和恒等函数作为AE神经网络的激活函数。通过累积贡献率方法选择好隐藏层的节点个数K，设置好训练次数。选择Adam算法作为优化器来加速神经网络的训练。将原始训练数据x加入噪声之后送入AE进而形成RAE模型。RAE模型随着训练次数的增加，损失函数越来越小，编码器神经网络的权值参数与偏置参数也在不断的更新，当损失函数的值慢慢下降并最后收敛趋于稳定之后，RAE的训练阶段完成。得到最小化的损失函数和RAE模型参数值。

RAE模型训练完成之后，原始训练数据x被分成输入数据的重构r*(x)和重构误差ξ*(x)两部分。分别对应于RAE的模型空间和残差空间。如式(15)所示：

x=r*(x)+ξ*(x)

(15)

r*(x) 和ξ*(x)分别对应于输入向量x的输出重构值和残差。在训练阶段，x在模型空间的投影就是模型输出r*(x)，而在残差空间的投影就是模型重构误差ξ*(x)，与测量噪声ε成正比关系。

2.3 RAE故障检测方法

RAE模型训练完成之后，将未加入噪声的原始数据x送入离线训练好的RAE模型中得到输出的重构r*(x)。训练好的RAE模型将原始数据空间分为模型空间和残差空间，其中模型空间对输入变化具有鲁棒性，而残差空间对输入变化敏感。所以在残差空间选择SPE统计量作为故障监测统计量。RAE模型的训练数据SPE统计量为

SPER=(r*(x)-x)T(r*(x)-x)

(16)

选择核密度估计法(KDE)来计算残差空间统计量SPER的阀值SPE_lim，这个阀值就是之后测试阶段判断是否存在故障的控制限。

3 基于TSNS-RAE的故障检测方法

将TSNS与RAE进行结合，形成TSNS-RAE故障检测方法。TSNS-RAE故障检测流程图如图3所示。TSNS-RAE模型故障检测主要分为离线建模和在线监测两个阶段。

离线建模阶段和在线监测的步骤如下。

离线建模过程：

1)对正常工况运行下的原始数据进行时空近邻标准化处理得到标准样本X。

4)将未加入噪声污染的标准样本X送入训练好的RAE模型之后，在残差空间计算重构误差从而求得SPE统计量。

5)利用核密度估计方法求SPE统计量的控制限SPE_lim。

在线监测过程：

1)从在线过程获得新的测试集数据并运用TSNS进行预处理得到Xt。

2)将Xt直接送入离线过程训练好的RAE模型并获得输出的重构值r*(Xt)。

3)计算在线监测时的SPE统计量并检查其是否超过离线过程设定的控制限SPE_lim。若超过控制限就表示发生故障，若没有超则表示正常。

4 数值案例仿真

使用一个动态非线性的数值案例过程来进行仿真。通过z-score，NS，TSNS这3种标准化方法的纵向对比来证明TSNS预处理对多模态过程检测有着重要作用。数值案例过程有两个输入变量θ，t和两个输出变量x1，x2，模型如下：

(17)

其中：a为过程参数，本文取为0.3，e1和e2为随机噪声。过程正常运行产生500个样本作为建模数据。再次，让过程正常运行，但从2π时刻起在变量t上添加幅值为-3的阶跃型扰动信号，共产生500个样本作为测试数据。分别使用z-score标准化方法，NS标准化方法，和TSNS标准化方法对训练数据和测试数据进行标准化处理，其中NS标准化的近邻数N=4，TSNS标准化的时间近邻数K=4，空间近邻数N=5，数据经过3种方法标准化之后的结果如图4所示。

图4 3种标准化方法对多模态数值例子的处理结果

通过对图三的几种标准化方法相比较可以发现，普通的Z-Score标准化方法无法将故障数据与正常数据进行分离。NS标准化方法只考虑空间上的近邻，忽略时间上的近邻，无法消除过程动态性，所以一部分故障可以与正常样本分离，而另一部分故障则没有分离出来。TSNS标准化方法同时考虑了时间和空间上的近邻，并且可以完全将故障样本与正常样本实现分离。

完成了对训练数据的标准化处理之后，我们给标准化的数据额外加上高斯噪声送入AE中形成RAE模型并进行训练，隐藏层的维数设置为1，隐藏层的激活函数选择sigmod函数，输出层激活函数选取恒等函数。优化算法选择为Adam优化算法，训练次数设置为1 000次。用训练数据训练好RAE模型之后，根据核密度估计法在残差空间求SPE统计量的控制限SPE_lim，然后将校验数据和故障数据合并当成测试数据集进行标准化处理之后送入RAE模型，得到测试集的SPE统计量并和SPE_lim进行比较进而监测故障，为了方便观测图形，我们算SPE相关统计量时按照以10为底取其对数。3种标准化方法的故障检测图如图5所示。

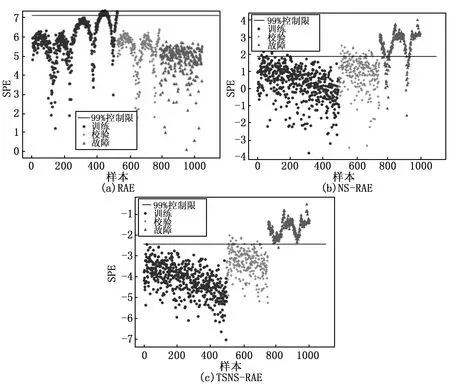
图5 3种方法对多模态数值例子故障检测结果

表1是RAE、NS-RAE、TSNS-RAE三种方法对多模态数值例子的故障检测误报率和检测率的结果对比。从表1中可以看出，Z-Score标准化之后的RAE检测结果最差，虽然没有误报，但是也没有检测出任何故障。NS-RAE故障检测效果较RAE有一定的提升。而TSNS-RAE方法的故障检测效果比RAE和NS-RAE方法的故障检测效果都要好，通过这3种方法的纵向对比可得知TSNS-RAE方法有较低的误报率和更高的检测率，更好地验证了TSNS在处理负杂多模态数据时的优越性。

表1 多模态数值例子的检测结果对比

5 青霉素生产过程数据仿真

青霉素生产发酵过程是一种具有时变性，不同操作阶段动态有不同特性，线性化程度不同以及非高斯性特点的典型的多模态生产过程。青霉素发酵过程中的代谢变化分为菌体生长，青霉素合成和菌体自溶3个阶段[18]。图6给出了青霉素发酵过程工艺流程图。

图6 青霉素发酵过程工艺流程图

本文采用pensim仿真平台生产青霉素数据，基于RAE，NS-RAE，TSNS-RAE算法进行故障检测。pensim仿真平台是由Cinar教授为首的研究小组创建开发的一款仿真软件，专为研究青霉素发酵过程而设计。pensim仿真平台在故障检测研究中有着十分广泛的应用[19]。同时由于其平台数据具有多模态过程数据的特点，为验证深度学习方法在多模态过程故障检测与诊断方面带来了很多便利。该平台有5个输入变量控制发酵过程参数变化，9个过程变量是菌体合成及生长中产生的，5个质量变量影响青霉素的产量[20]。设定仿真时间为400 h，采样间隔为0.5 h，先在正常工况下产生一组数据作为离线训练样本。青霉素发酵过程可以在通气率、搅拌功率和底物流速率这3个变量上引入干扰，分别有斜坡和阶跃两种干扰模式，通过调整两种模式的幅度、干扰引入时间和终止时间来产生故障。本文采取了青霉素发酵过程中的12个主要变量进行实验，同时设置了6种不同类型的故障作为待检测样本来验证所提TSNS-RAE算法的有效性，故障类型如表2所示。

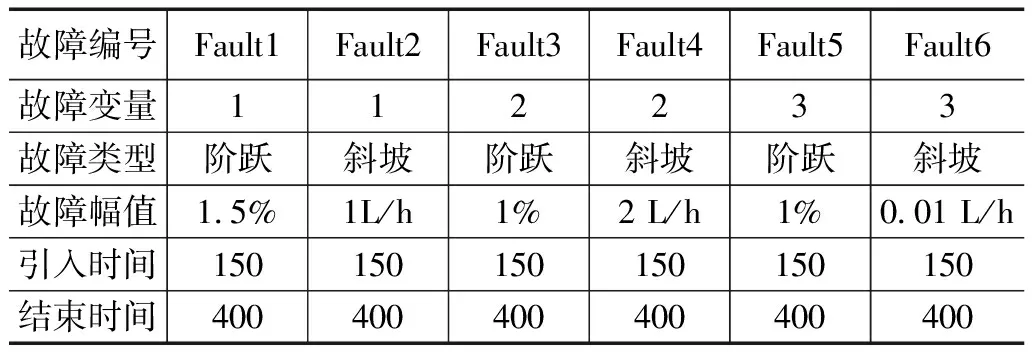
表2 青霉素生产过程的6种故障类型

基于数据驱动的故障检测最常用的检测方法是主成分分析(PCA)算法和K近邻(KNN)算法。将这两种检测方法和TSNS相结合，形成TSNS-PCA和TSNS-KNN算法。选用TSNS-RAE算法法来进行故障检测，并将其检测结果与TSNS-PCA，TSNS-KNN进行横向比较。TSNS方法的时间近邻个数N=5，空间近邻个数K=5。这些故障检测方法均以置信水平为99%来确定监测模型的控制限；其中PCA依据85%的累计贡献率来选取数据降维之后的主元个数。KNN算法的近邻个数k=5。RAE模型依据85%的累计贡献率选取编码器隐藏层节点个数为6；激活函数依旧选择Sigmod函数和恒等函数，选择Adam算法为优化器加速RAE的训练。RAE的训练次数设置为1 500。完成编码器的建模与故障检测之后。我们选择故障3和故障6的检测结果来作图，为了更好的图形显示效果，SPE相关统计量按照以10为底取对数。检测效果图如图7和图8所示。测试所用的不同方法的故障检测率和误报率均列在表3和表4中。

表3 不同方法的故障检测率/%

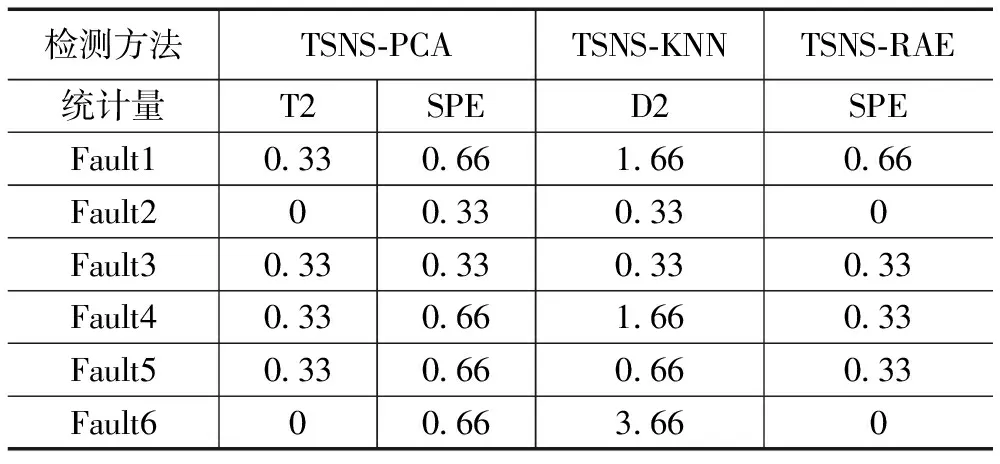
表4 不同方法的故障误报率 %

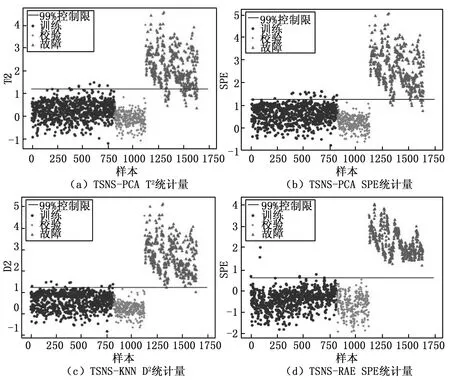
图7 不同方法对故障3的检测结果图

图8 不同方法对故障6的检测结果图

PCA作为最常用的故障检测方法，将过程数据分成降维之后的主成分空间和残差空间，分别对应T2统计量和SPE统计量，PCA原本只适用于单模态正态分布的数据，TSNS方法与PCA的结合消除了青霉素生产过程的多模态和动态性提升了PCA的检测效果。但是PCA无法考虑过程的非线性，所以TSNS-PCA的检测率与TSNS-KNN和TSNS-RAE相比效果不是很好。由故障3和故障6的实验结果图可以更直观的看出检测率较低。

KNN检测方法使用过程数据样本与其前k个近邻样本的距离平方和D2作为统计量，KNN方法考虑了工业过程的非线性，与TSNS方法结合之后对于多模态故障检测有着不错的检测效果，在检测率上会比PCA方法更好一点，误报率较高，故障1，故障4和故障6有着很高的误报率。由故障6的检测结果图可以更直观的看出校验数据存在着误报。结合检测率与误报率，整体的检测效果不如TSNS-RAE。

RAE作为深度学习方法，与传统的基于数据驱动的方法相比，有着更好的特征提取和数据降维效果，训练模型的损失函数越小，RAE对原始数据的重构越效果好。同时RAE模型有着抗噪性和鲁棒性。对青霉素数据使用TSNS-RAE方法进行故障检测，基本都有较好的故障检测效果。由表3可知，故障2，故障3，故障5和故障6的SPE统计量的检测率都达到了100%，故障1和故障4 的SPE统计量的检测率分别达到99.1%和99.6%。由表4可知整体的误报率都比较低。因此结合整体的检测率与误报率，通过对TSNS-PCA、TSNS-KNN、TSNS-RAE三种方法进行横向对比可知TSNS-RAE对于复杂多模态过程有着更好的检测效果。

6 结束语

根据多模态工业生产过程的数据特点，本文提出了一种基于TSNS-RAE的故障检测方法。通过数值案例，将TSNS方法与常用的Z-Score方法、NS方法方法进行比较，突出TSNS方法在预处理复杂多模态数据时的优势。通过青霉素生产过程实验，将TSNS-RAE与TSNS-PCA、TSNS-KNN进行横向对比，结合检测率与误报率，突出了TSNS-RAE在处理复杂多模态工业过程的优越性。

自动编码器除了鲁棒自编码器之外，还有堆叠自编码器，正交自编码器，变分自编码器等。每一种编码器都有各自的优势，今后的实验可以针对不同的工业过程将TSNS方法与其他编码器模型进行结合进行故障检测。