基于强度折减法的坑中坑整体稳定性数值模拟分析

2023-09-27陈林靖孙瑞轩罗一鸣

城市地质 2023年3期

陈林靖　孙瑞轩　罗一鸣

摘要：近年来国内外发生了多起因设计计算过程中忽略了内外坑的影响而造成坑中坑基坑失稳的重大事故，因此坑中坑的整体稳定性分析问题亟待解决。为解决此类问题，文章借助ABAQUS建立三维坑中坑有限元模型，采用强度折减法分析坑中坑基坑内外坑相互影响规律及坑中坑基坑破坏形式，并与传统理论计算方法进行对比。结果表明：主动区塑性区范围及滑裂面位置主要受外围护结构深度影响；坑中坑基坑内外坑间距增加，基坑安全系数不断逼近极限值。

关键词：强度折减；坑中坑；稳定性；极限破坏；安全系数；数值模拟

Numerical simulation of overall stability for pit in pit with strength reduction method

CHEN Linjing， SUN Ruixuan， LUO Yiming

（Institute of Geotechnical Engineering， Fuzhou University， Fuzhou 350108， Fujian， China）

Abstract： Recently there have been major accidents at home and abroad， in which pit in pit lost stability due to neglect of the influence of the inner and outer pits in the process of design and calculation. Therefore， it is necessary to carry out analysis of overall stability for pit in pit. In this paper， the strength reduction method was used to analyze the stability of the interaction law and the failure form of the pit in pit in comparison with the traditional theoretical calculation method. The results show that the plastic zone range of the active zone and the location of the slip surface were mainly affected by the depth of the outer protection structure. With the increase of pit spacing， the safety factor of foundation pit was approaching the limit value. Numerical simulation was conducted to study the influence of pit spacing on the overall stability of pit in pit.

Keywords： strength reduction; pit-in-pit; stability; ultimate failure; safety factor; numerical simulation

近年來，我国工程实践经验和科研理论水平达到了新的高度，但对于坑中坑基坑的设计规程尚未有系统的、具体的规定。坑中坑支护设计是基坑工程中的关键一环，为了保证工程的安全性，基坑设计需要考虑内外坑间距等多种因素对基坑整体稳定性的影响。在实际工程中，国内外发生了多起因设计计算过程中忽略了内外坑的影响而产生工程事故，轻则使基坑主体结构位移偏大，重则造成基坑失稳危害整个基坑工程的安全（王曙光，2005）。

基坑整体稳定性分析主要采用数值模拟法。有限元软件打破了传统理论计算的诸多限制，极大程度上提高了极限分析法的求解精度以及适用性。商兆涛等（2022）采用FLAC 3D软件以及强度折减法计算结果显示，随着开挖深度增加，安全系数不断降低并逐渐趋于平缓，围护结构的深度对基坑稳定性有一定的影响；薛子龙等（2021）通过分析发现坑中坑内外坑间距以及内坑深度的增加会使基坑整体变形增加，基坑的稳定性降低；何忠明等（2022）利用FLAC 3D分析了基坑开挖工程中支护结构的水平位移及周围土体地表沉降的变化规律；钱天平（2012）运用Plaxis数值模拟和正交试验相结合的方法得出坑中坑对基坑的影响不能忽视，选取等效深度代替基坑深度进行计算分析时要慎重；杨才等（2019）为了更深入地探究坑中坑整体稳定性的影响因素，对坑中坑3个主要尺寸参数进行了控制变量研究；杨明等（2014）与何岩（2016）运用有限元软件对坑中坑土体强度参数进行折减破坏，得出当内外坑间距较近时必须考虑内坑对外坑的影响；郝志斌等（2019）针对澳门某深基坑支护，采用有限元法得出深基坑局部挖深对基坑整体稳定影响较大，可影响内撑系统轴力分布。以上研究以数值模拟方式论证了坑中坑整体稳定性问题。

可见，国内外在坑中坑相关问题的研究与基坑有限元极限分析中已经取得了一些成果，但对于不同内外坑间距对坑中坑整体稳定性影响的研究还较少，特别是针对围护结构埋深达60 m的超深坑中坑基坑开挖工程还未有研究（龚晓南，2005；郑颖人等，2005）。本文借助ABAQUS有限元软件，采用强度折减法对坑中坑基坑内外坑相互影响规律及坑中坑基坑破坏形式进行了稳定性分析，并与传统理论计算方法进行对比。旨在揭示坑中坑基坑内外坑互相影响的规律，同时探究软土地基坑中坑主被动区整体破坏形式及塑性区发展机理，为软土地区相似坑中坑基坑工程的设计提供依据。

1 极限分析中基坑破坏的判据

对于岩土工程中的整体失稳破坏，一般表现为岩土体沿破裂面发生滑落或坍塌，岩土体不能继续承载，滑裂面达到极限平衡状态，并且使得滑面的位移与应变突增。对于基坑失稳的判断依据主要有3种：

1）塑性区是否贯通。当岩土体塑性区贯通时，即可以认为岩土体发生破坏。通过ABAQUS软件处理后，塑性应变将以云图的方式准确清晰地显示出塑性应变值的大小、塑性区位置及塑性区范围的发展状况（连镇营等，2001；栾茂田等，2003）。

2）特征部位位移是否发生突变。当特征部位X、Y、Z方向的位移发生突变，产生拐点，判断已失稳，则在3个方向中取最大者为基坑安全系数（李土亮等，2016）。

3）有限元数值计算是否收敛。非线性有限元方程组的迭代求解计算至基坑达到极限平衡状态，则显示不收敛。但应用于岩土工程中有一定局限性，适用性差（Griffiths et al.，1999；Dawson et al.，1999）。

目前国内外仍没有对岩土体整体失稳破坏判据形成统一认识。郑宏等（2002）认为是土体滑面上全部达到极限平衡时发生整体失稳破坏，因此第一种破坏判据为岩土体滑面上塑性贯通；赵尚毅等（2005）将有限元计算是否收敛作为边坡破坏的依据，并认为通过岩土体塑性贯通表示岩土体发生破坏是合理的，但塑性区贯通是发生破坏的必要条件并非充分条件，还需要进一步观察岩土体是否产生很大的且无限发展的位移和塑性变形，即在有限元计算中产生较大的塑性应变和位移突变。

本文为真实工程案例分析，以特征部位位移的突变性作为基坑失稳的判断依据相较于塑性区贯通及有限元计算不收敛更符合工程实际。即通过特征部位位移突变来确定基坑的整体稳定安全系数，并且通过塑性区的贯通对其进行补充。

2 流动法则的选取

屈服准则采用Mohr-Coulomb屈服准则（郑颖人等，2019），即：

式中，F为塑性势函数，I1为应力张量第一不变量，J2为应力偏量第二不张量，θσ为应力罗德角（°），c为土体黏聚力（kPa），φ为土体内摩擦角（°）。

流动法则的选取：若ψ=φ（膨胀角等于内摩擦角），为关联流动法则；若ψ≠φ，为非关联流动法则。岩土工程材料不适应关联流动法则，此法则计算出的土体变形与实际差异较大（李春忠等，2006）。为尽可能地接近实际情况，本文将采用非关联流动法则，且取膨胀角为内摩擦角的二分之一（孔位学等，2009）。

3 坑中坑极限破坏数值模拟分析

3.1 工程概况

在建的潘墩站（原会展中心站）为福州市地铁六号线的第一个车站，车站位于仓山区潘墩路与林浦路的交叉口，沿林浦路东西向布置，地下三层岛式车站。主体采用明挖顺作法施工，两端区间采用盾构法施工。项目实景相片如图1所示，基坑平面如图2所示。

3.2 模型的建立

坑中坑外坑采用? 850 mm @ 600 mm的SMW工法桩结构作围护，内坑围护结构则是厚1 m、深47.8 m的地下连续墙。SMW工法桩桩身采用P42.5级普通硅酸盐水泥，桩长24.3 m，采用隔一插二法内插H700 × 300 × 13 × 24型钢。对于SMW工法桩，将其按等效刚度原则折算成厚度为h的地下连续墙，折算厚度由下列任一公式换算：

式中，h为折算后的地下连续墙厚度（mm），d为围护桩直径（mm），t为围护桩净间距（mm）。

取模型水平方向外边界到工法桩止水帷幕外侧为120 m，结合基坑情况建立一个长×高（即沿x、y方向）为272.7 m × 80 m的土体模型，模型两侧边界限制径向位移（X方向），模型顶面和前后面均为自由边界，模型底部限制X、Y方向位移，如图3所示。由现场勘察报告得到的土体及支护结构的相关参数见表1。

图4所示为无内坑情况时有限元分析所得的塑性滑裂面以及特征点水平位移拐点。其中FS为基坑整体稳定安全系数，U1为基坑土体侧向位移。为了验证有限元模型的合理性，同时采用理正深基坑7.0软件（软件采用传统的瑞典条分法以验算最危险的圆弧滑动面）对坑中坑无内坑情况进行整体稳定性分析，并与有限元极限分析法结果对比，如图5所示。

结果表明，通过理正岩土软件计算的基坑整体稳定安全系数（FS）为2.43，与数值模拟结果所得的基坑整体稳定安全系数（FS=2.51）结果非常接近，两者相差仅3%，由此可见用该有限元模型对基坑进行整体稳定性安全分析是合理的、科学的。

3.3 坑中坑整体稳定性极限分析

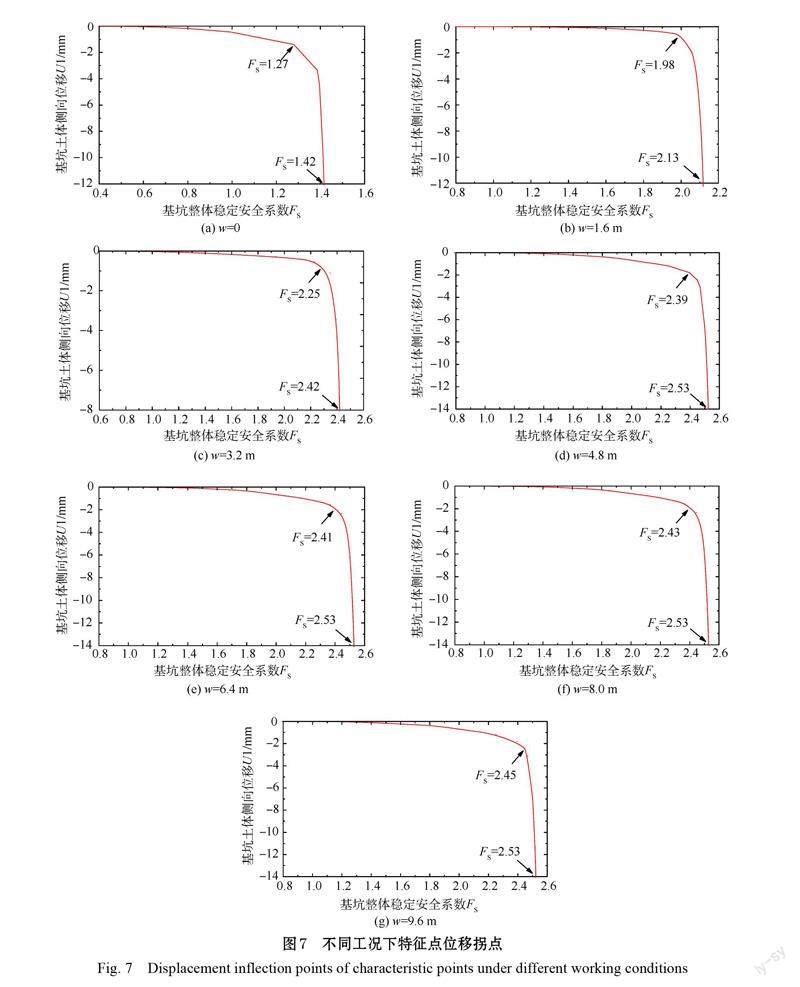
坑中坑整体的稳定性与内坑的尺寸有着极大的关系，主要体现在内坑深度h、宽度b以及内外坑间距w共3个方面。本文假设内外坑间距w分别为0、1.6 m、3.2 m、4.8 m、6.4 m、8.0 m、9.6 m，探究内外坑间距对坑中坑整体稳定性的影响。各模拟计算工况下坑中坑整体稳定破坏时的塑性滑裂面以及特征点水平位移拐点，见图6、图7。

1）整体破坏滑裂带及塑性分析

基坑破坏塑性区是由所有进入塑性应力状态点集成的区域，而剪切带就是基坑最终破坏时的潜在滑裂面，从坑中坑整体稳定破坏时塑性区的范围（图）来看，除了无内坑的情况，坑中坑主动区塑性区范围基本处在24～28 m范围内，被动区塑性区范围在9.5 m到18.6 m之间变化。坑中坑整体稳定破坏时的塑性区范围要远大于滑裂面范围，在坑中坑主动区的可见塑性区范围大致为滑裂面范围的2倍。

从基坑受内坑影响程度上分析，在有内坑的情况下，主动区塑性区宽度在26 m左右變化，滑裂面宽度基本在8 m左右，两者受内外坑间距w的影响甚小。由此可猜测主动区塑性区范围及滑裂面位置主要受外围护结构深度影响，此时塑性区范围约为外坑地连墙深度的1倍，而滑裂面位置约在外坑地连墙深度的0.5倍，滑裂角约为45°。

如图4，对没有内坑的坑中坑模型进行整体稳定性分析，得到的基坑整体稳定安全系数（FS）为2.15，塑性区同样发展到了基坑顶面且产生明显的滑裂面，形成了贯通区域。与有内坑但是内外坑间距w为0的坑中坑（图6-a）相比，虽然塑性滑裂面均已贯通，但有内坑时主动区塑性区范围与塑性应变数值均变大，且形成了绕地下连续墙底的弧形塑性区，此时的基坑整体稳定安全系数（FS）为2.17，两者安全系数差异超过了50%，因此在设计基坑支护时必须考虑内坑的影响。

处于坑中坑基坑被动区的塑性区范围受内坑间距影响较大，内外坑距离w为0时，如图6-a，外坑与内坑深度均为23 m，地下连续墙入土深度约为24.3 m。此时塑性区范围37.5 m，约为地下连续墙入土深度的1.5倍；滑裂面外边缘位于坑面x=16 m处，约为地下连续墙入土深度的2/3；滑裂面内边缘位于地下连续墙深度12 m处，约为地下连续墙入土深度的1/2，平均滑裂角为45°。

内外坑距离w为1.6 m时（图6-b），外坑深7.6 m，内坑深23 m，内工法桩入土深度为49 m，此时内外坑土体一起进入塑性应变状态。与申明亮（2013）等学者研究的理想坑中坑模型基坑破壞模式不同的是，本文坑中坑实例模型发生整体破坏时的被动区土体并没有产生明显塑性滑裂带，滑裂带仅出现在主动区土体。笔者分析是由于内侧地下连续墙较深，仅凭土体自重无法使塑性应变在土与土之间传递至被动区土体（形成绕桩底的弧形塑性滑裂带），而是直接借助刚性工法桩向被动区土体传递挤压应力，从而在被动区产生塑性区但不至于产生塑性滑裂带。此时由于内外坑距离较短，内外坑隔着桩墙的塑性区像是“贯通”了起来，有了工法桩的嵌入，基坑整体稳定安全系数（FS）从1.27提高为1.98，增幅达56%。

内外坑距离w为3.2 m时（图6-c），被动区塑性范围进一步扩大到13.7 m，而滑裂面外边缘仍在x=16 m处破坏，塑性应变进一步减小，基坑整体稳定安全系数（FS）增大到2.25。随着内外坑间距不断增大（w分别为4.8 m、6.4 m、8.0 m、9.6 m），滑裂面外边缘位置一直维持在x=16 m左右无变化，被动区塑性区范围随着内外坑间距增大而相应增大，但变化规律总体不变。由图6-f和图6-g可发现，随着内外坑间距的增大，被动区塑性范围逐渐脱离外工法桩内侧。内外坑的塑性区真正意义上并不是贯通相连的，不管是内坑还是外坑，塑性区其实都是集中在桩墙两侧，因为此处土体的挤压应力是最大的，极易发生塑性应变。

2）整体稳定安全系数分析及统计

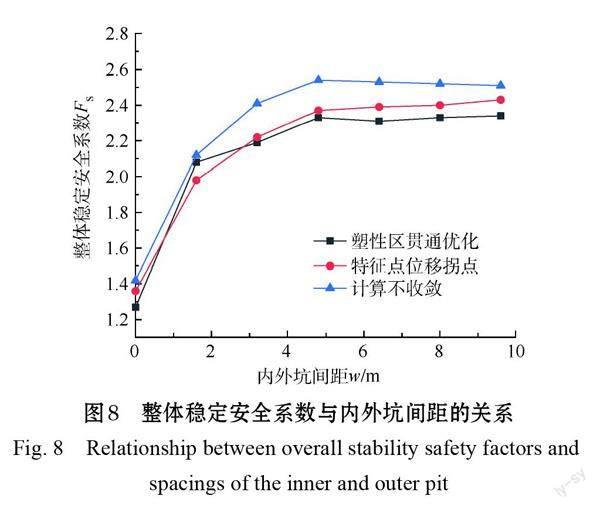
常用的土体失稳判据有3种，与之相对应的是3个不同的稳定安全系数。现按照计算不收敛、塑性区贯通、特征点位移拐点3种失稳判据，将坑中坑各工况下对应的稳定安全系数与内外坑间距w的关系绘制在图8中。

以特征点位移拐点为主要判据进行分析时，由图7-a可知，当内外坑间距w为0时坑中坑整体稳定安全系数最小，约为1.27。由图7-b可知，无内坑时坑中坑整体稳定安全系数（FS）为2.51，稳定性在各种工况中最高。上述两模型（无内坑与内外坑间距为0）内外坑间距相同（都为零），最大的差别在于土体开挖深度不同，却导致了最大的基坑稳定性差异，由此可见土体开挖深度在某种程度上对基坑稳定性的影响程度远大于内外坑间距的影响。通过分析可得，当较深的坑中坑开挖在外坑的围护结构周围时，在基坑被动区土体的作用下使得围护结构产生抗力损失进而使得围护结构向坑内的位移趋势增加，最终导致基坑整体失稳。

随着内外坑间距w的增加，坑中坑整体稳定安全系数不断增大，且越来越逼近无内坑工况下的基坑整体稳定安全系数。观察可知：当内外坑间距w=0～3.2 m时，基坑整体稳定安全系数增长速率最快；内外坑间距w=3.2 m时，基坑整体稳定安全系数已达到了2.25；而当w≥4.8 m时，基坑整体稳定安全系数增长变得非常平缓，基本在2.43左右。

与此同时，我们发现3种不同的判据所得整体稳定安全系数均呈现出一定的规律。以计算不收敛为判据所得整体稳定安全系数曲线整体上要高于其他2种判据所得安全系数曲线。有分析认为，有限元计算不收敛大概率发生在塑性区贯通和特征点位移拐点之后（Grifffiths et al.，1999）。在有限元软件ABAQUS计算最大迭代次数内计算不收敛表明没有出现能满足破坏准则和整体平衡的应力分布状态，经过残余力多次的迭代，此时土体早已破坏，故以计算不收敛为判据所得整体稳定安全系数整体上会偏大一些；而以塑性区贯通与特征点位移突变为判据所得的安全系数曲线两者不相上下。理论上，材料的抗剪强度随着基坑整体稳定安全系数的增大而不断降低土体塑性区范围，直至产生连续的塑性滑动带（即塑性区贯通），此时因为基坑或边坡内开始发生滑动破坏，基坑特征点位移突然增大。

4 结论

1）对坑中坑进行整体稳定性分析时，主动区塑性区范围及滑裂面位置主要受外围护结构深度影响，受内外坑间距影响较小，在坑中坑主动区的可见塑性区范围大致为滑裂面范围的2倍。在具有坑中坑的实际工程中应按照规范施加外围护结构。

2）坑中坑基坑破坏时，不管是内坑还是外坑，塑性点更多地集中在桩墙两侧，因为此处土体的挤压应力最大，极易发生塑性应变。土体开挖深度对基坑稳定性的影响程度大于内外坑间距的影响。实际工程中尽量避免在外坑围护结构附近开挖深度比较大的坑中坑。

3）在极限分析时，以计算不收敛为判据所得稳定安全系数整体上要高于以塑性区贯通及特征点位移拐点为判据所得安全系数。而由于基坑发生滑动破坏时往往同时伴随着特征点位移突变，故后2种判据所得安全系数较为接近。

参考文献

龚晓南，2005. 关于基坑工程的几点思考［J］. 土木工程学报（9）：99-102+108.

郝志斌，王道伟，2019. 基于Plaxis的深基坑局部挖深对支护结构的影响模拟［J］. 水运工程（9）：309-315.

何岩，2016. 中航廣场二期深基坑支护结构分析与研究［D］. 南昌大学.

何忠明，王盘盘，王利军，张耀，陈勇超，2022. 超大深基坑开挖变形演化规律及优化设计［J］. 长沙理工大学学报（自然科学版），19（3）：69-77.

孔位学，芮勇勤，董宝弟，2009. 岩土材料在非关联流动法则下剪胀角选取探讨［J］. 岩土力学，30（11）：3278-3282.

李春忠，陈国兴，樊有维，2006. 基于ABAQUS的强度折减有限元法边坡稳定性分析［J］. 防灾减灾工程学报（2）：207-212.

李土亮，刘宝奎，阮东伟，2016. 基于ABAQUS强度折减法的边坡稳定性影响因素分析［J］. 内蒙古公路与运输（3）：11-14.