模型未知LTI系统的数据驱动预测控制

徐 凯，陈 珺

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122)

0 引言

基于被控对象数学模型的现代控制理论自20世纪60年代被提出以来，已经形成了一套十分成熟的理论体系，并在工业过程、航空航天等领域中得到了大规模的成功应用[1]。然而，对于机理模型或辨识模型可获取但却带有无法描述性质的系统、模型复杂且阶数较高的系统、模型无法获取的系统这三类系统的控制问题，现代控制理论目前还未有较好的解决方案[2]。

数据驱动是一种利用被控系统的在线和离线数据实现系统基于数据的预测、评价、诊断、监控、决策和优化等各种功能的思想[3]。

在系统的控制问题之中，轨迹跟踪问题是一个十分值得研究的问题。在轨迹跟踪问题中，模型预测控制(MPC，model predictive control)是应用最广泛的控制方法之一，因为它允许在控制设计中考虑安全因素[4]，可以通过约束保障系统的稳定运行。使用模型预测控制方案的关键是一个精确的系统参数状态空间模型，但是这样的模型往往不能直接获取。因此将数据驱动的思想与之相结合变得很有意义。近年来，有许多学者对两者的结合进行了研究并发表了相应研究成果，文献[5]对Vienna整流器提出了一种利用电压和电流信息数据实现的超局部模型替代Vienna整流器精确模型的无模型预测电流控制方法；文献[6]针对时滞系统难以获取模型的情况，结合跟踪-微分器获取微分信息的能力，利用Smith预估器预测未来时刻输出有效提高了控制系统的响应速度；文献[7]中使用数据驱动的神经元预测器拟合系统的模型结合预测控制实现了ASV的速度控制；文献[8]结合了深度强化学习和预测控制实现了一种高精度的无人驾驶方式；文献[9]通过子空间预测控制方案构建了电机的电压平衡模型，从而实现了电机的无偏移跟踪；文献[10]中采用深度学习训练通过Koopman理论简化得到的通用结构模型，实现了非线性模型的最优轨迹跟踪；文献[11]提出一种将循环神经网络与模型预测控制算法相结合的算法，在保持了控制器性能的同时，有效提升了算法执行速度并减少了存储数据占用的内存；文献[12]将子空间辨识和预测控制思想相结合并提出一种最优调优方法，简化了预测模型的建立过程，解决了控制器参数调整过程复杂的问题；文献[13]将模型预测控制与比例、积分、微分控制方案相结合，减少了传统模型预测控制方法调整的复杂度，并解决了其计算量大、系统动态性能易受影响的问题，同时将模糊理论与模型预测控制相结合，获得了比PID算法更好的抗干扰能力，同时减少了预测范围；文献[14]将数据驱动概念集成到鲁棒模型预测控制结构中，用数据估计模型替代预测，在解决了传统方法保守性高、计算困难的问题的同时提高了系统的闭环性能；文献[15]提出了一种全新的数据驱动模型预测控制方案，通过调整系统不同部分之间的耦合条件，将系统分为不同的子系统并通过分散的模型预估独立控制，有效提升了系统的稳定性。

虽然目前已经有很多种基于数据驱动的预测控制方法被提出，但都是利用系统的历史数据并根据具体被控系统的数学原理来进行建模，或者是使用神经网络等方法拟合出被控系统的模型，模型获取过程十分繁琐，同时获得的模型不具备通用性，在系统参数调整时模型精度显著下降，而且大都没有考虑测量噪声对系统控制效果的影响。

文中对于仅有测量数据可得的LTI系统提出了一种数据驱动的预测控制方案，根据系统行为学理论[16]和平衡子空间辨识方法[17]利用测量数据直接设计了控制器，解决了传统模型预测控制方法获取预测模型困难且控制律难以设计的问题，并考虑了系统测量数据中存在的随机噪声所带来的扰动对控制性能产生的影响，通过引入辅助松弛变量和L2正则化项抑制了噪声扰动，提高了算法的鲁棒性，最后采用多步滚动时域优化方法求解优化问题并对系统施行控制，实现了系统对设定值的轨迹跟踪。基于Python平台和CasADi工具箱对算法进行仿真验证，将所提方法应用于一个四容水箱系统并与同样基于数据驱动的子空间模型预测控制方法相比较，仿真结果证明了所提方法的有效性和优越性。

1 系统行为学理论

基于根据文献[16]中提出的系统行为学理论，一个动力系统可以被定义为一个三元组∑=(T，W，B)，其中T⊆R表示时间轴，W表示系统的信号空间包含该系统所有可能的输入输出信号，B⊆WT是系统的行为，B中的每个元素为系统的轨迹。文中考虑的是离散LTI系统，对于此类系统有以下结论成立：T=N，W=Rω是一个有限维度的向量空间，B是一个线性空间且满足B⊆σB(时延算子σ定义为σf(t)：=f(t+1))，同时B在点态收敛拓扑中是封闭的。综上所述，离散LTI系统按照系统行为学理论可以表示为∑=(N，Rω，B)。

对于该LTI系统的轨迹ω(t)∈B通常可以表现为式(1)：

R0ω(t)+R1σω(t)+…+Rlσlω(t)=0

(1)

其中：Rτ∈Ri×ω，τ=1，…，l，i表示等式的个数，ω表示信号空间的维数，l表示方程的阶数。定义多项式矩阵R(σ)为式(2)：

R(σ)=R0+R1σ+…+Rlσl∈Ri×ω[σ]

(2)

式(2)是一个i×ω的矩阵，每个元素都为时延算子σ的多项式。根据线性代数中核空间kernel的定义，式(2)可以表示为式(3)的形式：

ker(R(σ))：={ω|R(σ)ω=0}

(3)

因此B可以写为B：=ker(R(σ))。在前述定义下，对于系统的任意两个轨迹ω1，ω2∈B，存在ω∈B，使轨迹ω1在一定时间T后转变为ω2，如图1所示。

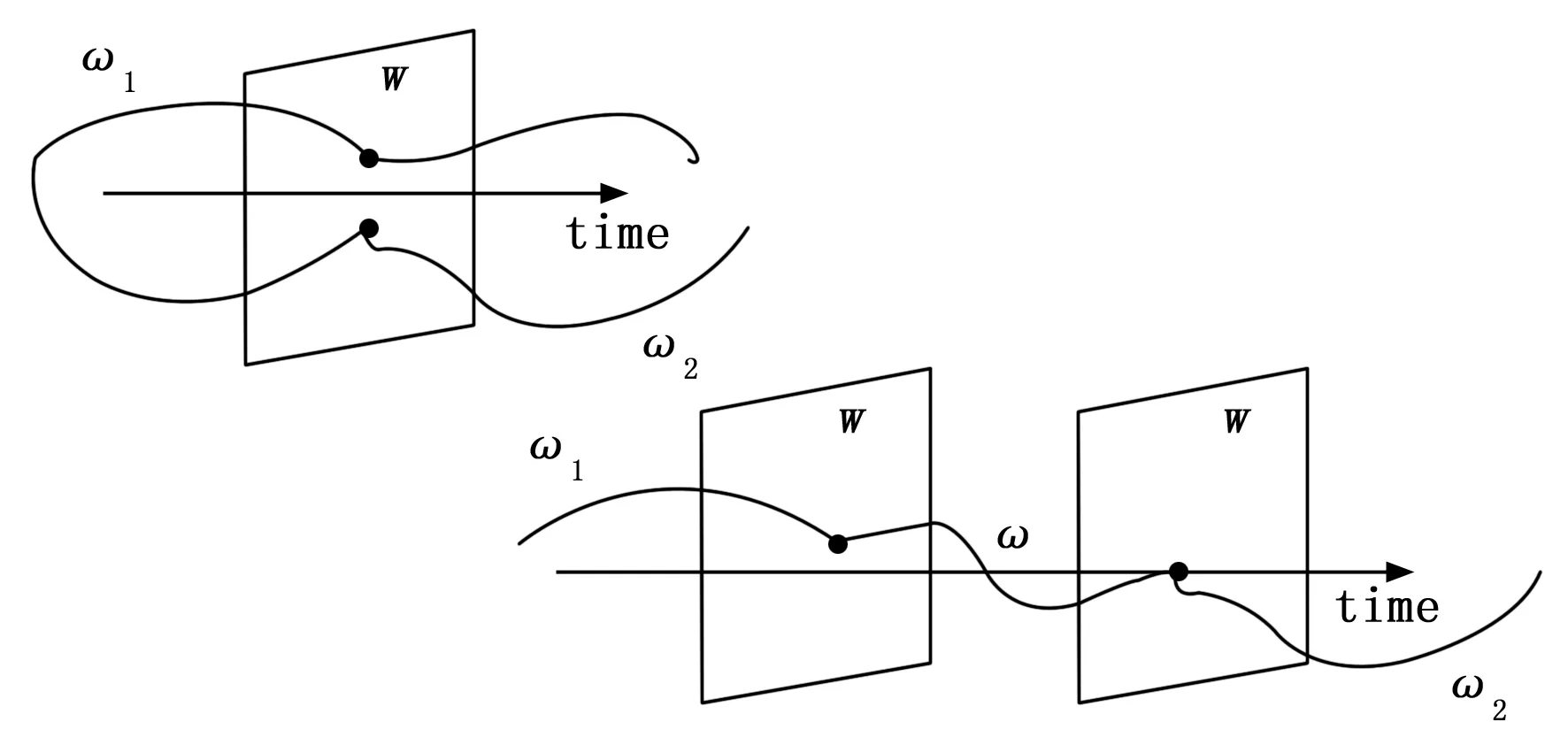
图1 系统行为学理论下LTI系统轨迹变化示意图

即对于同一个LTI系统，如果两条轨迹初始状态相同，被观测到的输出也相同，那么认为其过去的输入累积效果也相同。

2 平衡子空间辨识方法

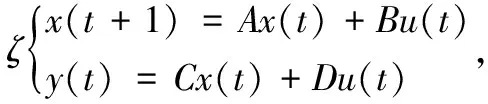
系统信号的时间序列为f=(f(1)，...，f(T))。定义该信号的块Hankel矩阵为：

HΔ(f)=

其中：Δ为有限时间平衡参数。根据以上算法。

算法1：输入：系统轨迹ω=(u，y)，系统阶数的上界Πmax，有限时间平衡参数Δ>Πmax。

步骤1：找到系统脉冲响应矩阵的前2Δ样本H(0)，…，H(2Δ-1)，并令H：=col(H(0)，…，H(2Δ-1))。

步骤5：通过求解线性系统等式

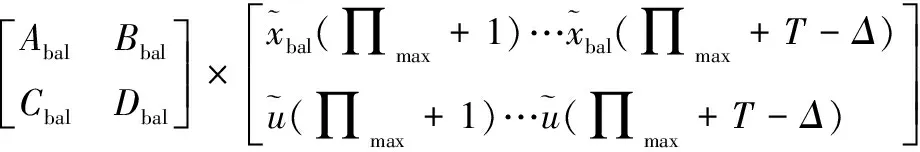
根据系统行为学理论，有以下基础引理。

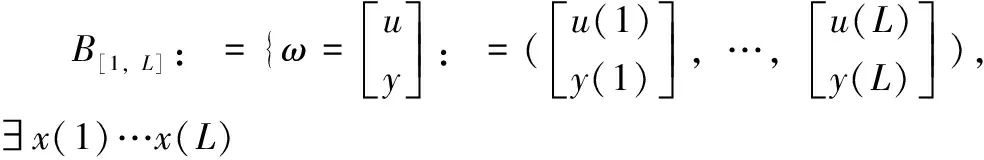
定义row dim为矩阵的块行数，Up，Uf，Yp，Yf如下：

其中：row dim(Up)=row dim(Yp)=lmax，row dim(Uf)=row dim(Yf)=2Δ。

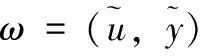
(4)

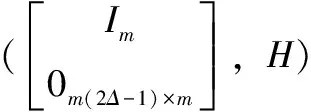
(5)

如上所述，可以将获得的数据分为过去和未来两个部分，据此提出算法2。

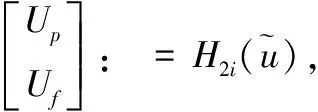
步骤6：通过代入求解前述算法步骤5中等式的可以获得系统相应的平衡表示Abal，Bbal，Cbal，Dbal。

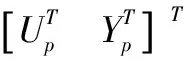
根据上述结论，在系统采集的数据满足充分持续激励阶时，该系统可被充分识别，可以通过历史数据确认系统的模型和当前状态。

3 算法原理及实现步骤

3.1 非参数模型的建立

根据第一节所述系统行为学理论，提出如下定义。把B中每个轨迹中[t1，t2]内的部分截断出来，组成新的集合(6)：

B[t1，t2]={ω：[0，T-1]→Rω|

∃υ∈B：ω(t)=υ(t) ∀t1≤t≤t2}

(6)

根据式(1)、式(2)、式(3)可以得到零空间式(7)：

rB={r∈Rω[σ]|rT(σ)B=0}

(7)

根据式(2)定义式(7)的阶数形式为式(8)：

每个元素的阶数均小于等于ψ}

(8)

考虑如下离散时不变系统模型(9)：

(9)

式(7)中u(k)∈Rm，x(k)∈Rn，y(k)∈Rp分别为系统的输入、状态和输出量，A，B，C，D是具有合适维度的矩阵，且满足(A，B)可控，(A，C)可观测。

从0时刻起，在系统(9)中采样长度为T的信号f：f∈B|[0，T-1]。定义一个Hankel矩阵如式(10)。

(10)

(11)

根据式(11)可以得到式(12)成立：

(12)

同样由于LTI系统的线性特性，可以得到式(13)成立：

colspan(HL(f))⊂B|[0，T-1]

(13)

定义1：假设信号f=[0，T-1]∩N→Rω当且仅当式(14)满足时持续激励L阶。

rank(HL(f))=Lω

(14)

其中：ω是信号空间W的维数，对于系统(7)有ω=m+p，即由输入和输出拼接成系统信号轨迹。

(15)

colspan(HL(f))=B|[0，T-1]

(16)

定理1的证明见文献[16]。

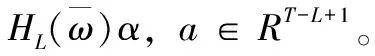
(17)

式(17)即为离散LTI系统的非参数模型，其完全由系统的输入输出数据构成，系统的任意一段长度为L的轨迹都可以由系统测量数据的Hankel矩阵的列线性张成。

3.2 算法实现

算法主要由数据采集，优化问题求解和滚动时域优化三部分组成。

对于数据驱动的控制方法，数据的采集是必不可少的。根据定义1和定理1的要求，采集的数据轨迹需要满足式(14)且必须采集自一条连续的系统轨迹。由于判断Hankel矩阵的秩比较困难，一般通过保证采集的数据点个数满足条件T>(m+1)(L+n)-1来保证定理1的条件成立。

控制系统结构如图2所示。

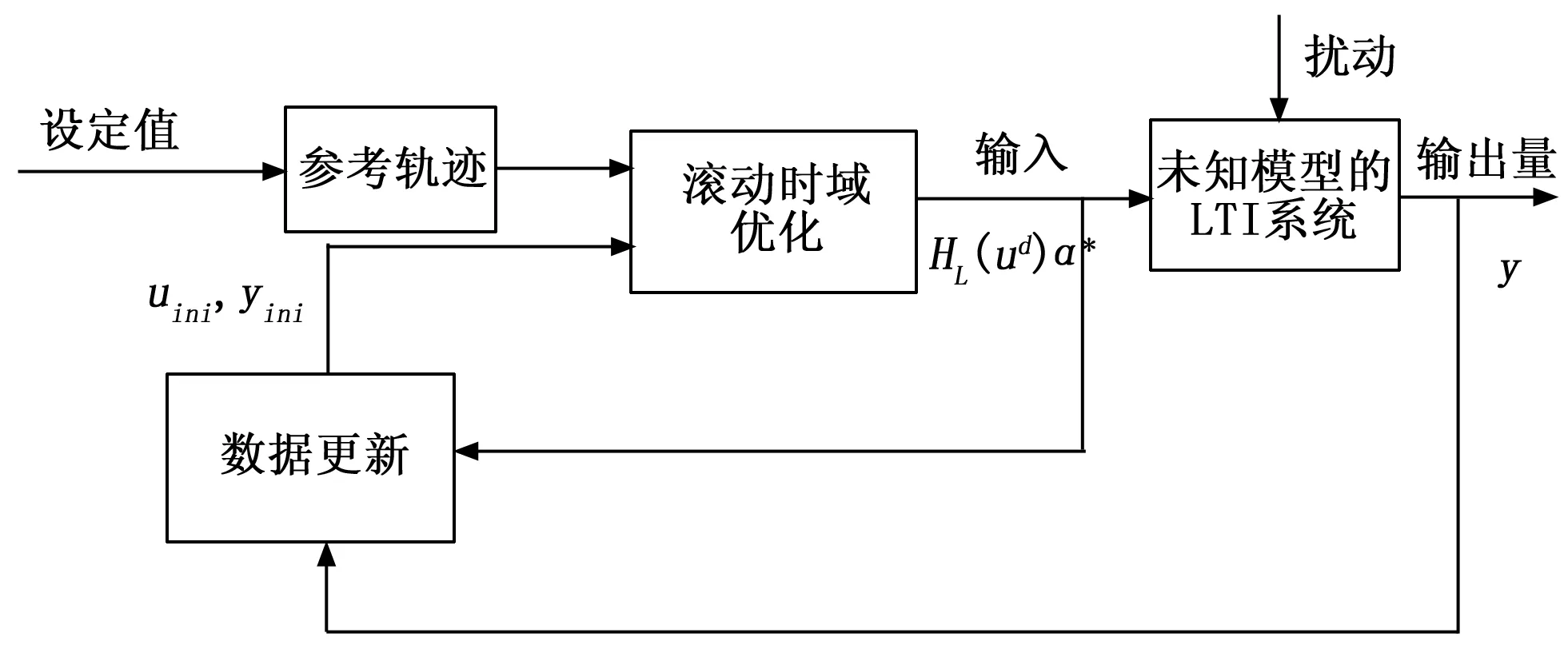
图2 基于数据驱动的预测控制系统结构框图

如图2所示，系统在每次决策过后更新当前数据。根据文献[17]中的平衡子空间辨识法，把式(17)分解为式(18)的形式：

(18)

用式(18)作为预测模型代替传统模型预测控制中如式(9)的系统状态空间模型表示和系统状态估计，设计目标函数如下式(19)：

(19)

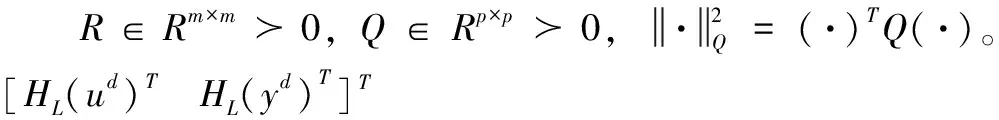
通过求解优化问题(19)可以得到对系统下一步采取的控制决策。

为了提升算法效率，减少迭代次数，采用多步滚动时域优化策略，一次预测多个未来值，其具体步骤如下。

步骤1：采样T对连续的系统输入输出数据构建如式(18)的系统非参数模型作为目标函数的约束条件，设置控制器基本参数如预测时域N，权重矩阵Q、R等。

步骤2：在t时刻，求解目标函数得到最优决策变量α*。

步骤3：计算最优输入序列u*=HL(ud)α*。

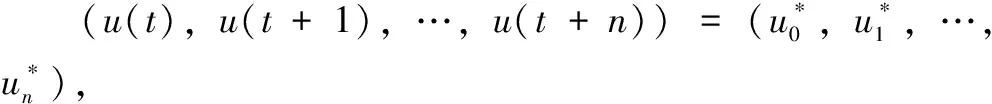
步骤5：令t=t+n，更新目标函数约束中的uini和yini为新测量得的Tini对输入输出数据。

步骤6：返回步骤2直到预测结束。

3.3 鲁棒性改进

对于系统测量数据中存在有界加性高斯噪声的系统，其输入输出测量信号模型为：

(20)

式(20)中的v(k)∈Rm、z(k)∈Rp为符合正态分布的有界加性高斯噪声。加入噪声扰动后如式(18)的约束条件将变得难以满足，此时对(19)进行以下改进。

松弛变量常被用于支持向量机SVM(support vector machines)，通过允许一些数据样本不满足硬间隔约束条件，可以防止SVM分类器过拟合，避免模型过于复杂，降低模型对噪声点的敏感性。L2正则项则可以约束松弛变量，同时可以使目标函数的求解变得稳定和快速。

引入松弛变量可以保证约束的满足，L2正则项则可以保证变量不产生过大的变化，改进后的目标函数如式(21)：

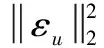
(21)

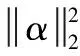
4 仿真实验

4.1 实验数据的采集

为了验证算法的有效性，采用一个典型的多输入多输出的四容水箱系统作为实验对象，并对该四容水箱的跟踪控制问题进行仿真验证。

根据四容水箱的工作原理，建立对象的非线性机理模型为式(22)[18]。

(22)

在平衡点(数据见表1)处对式(22)进行线性化处理，四容水箱系统的输入为水泵电压u=[u1u2]T，状态为水箱液位高度x=[x1x2x3x4]T，输出为水箱1和水箱2的液位高度y=[y1y2]T。水箱选取参数和初始条件如表1所示[19]。

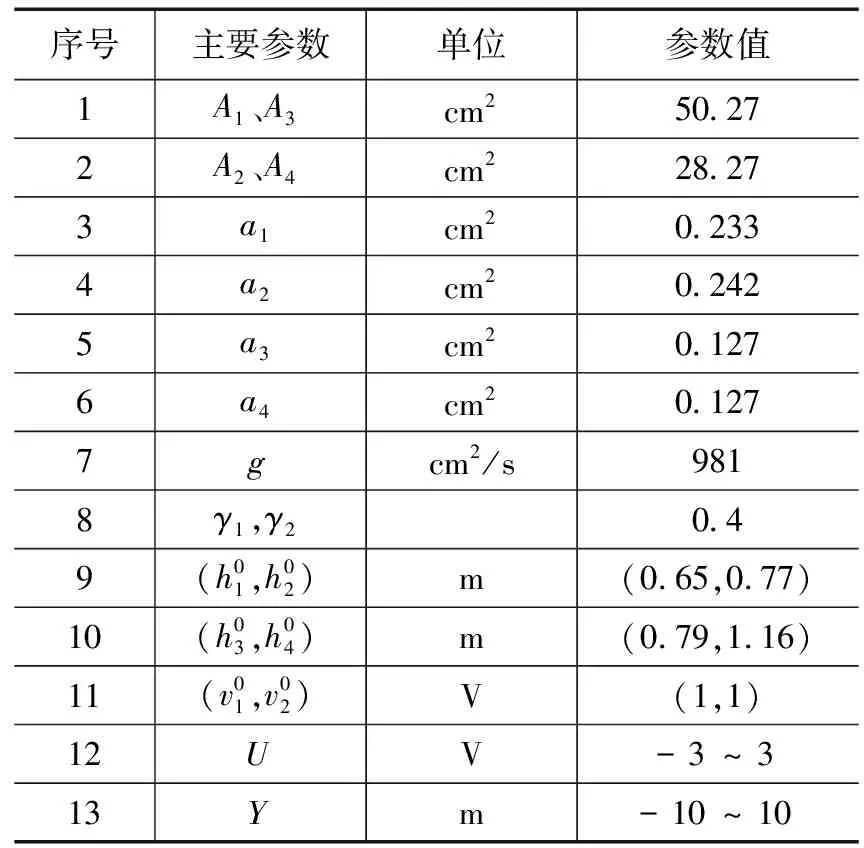
表1 四容水箱系统相关参数

输入选取范围在[-3，3]之间的随机激励信号，系统初始状态设置为零初始状态。对于四容水箱，输入和输出维度m=2，p=2，状态维度n=4。选取初始数据序列长度Tini=4，预测时域N=40，L=Tini+N=44，根据定理1的要求采样数据序列长度需要满足T>(m+1)(L+n)-1=143，因此选择采样数据点个数为T=150，采样间隔选取为0.1 s，总采样时间为15 s。采样输入输出数据序列为U(k)=[u1(k)，u2(k)]和Y(k)=[y1(k)，y2(k)]，采样数据如图3。

4.2 算法仿真验证

为了验证所提方法的有效性，先考虑测量数据中不含噪声的情况。选择ys=[0.65 0.77]T为参考轨迹。控制器参数选择为N=40，即预测时间为4 s，初始轨迹长度Tini=4，权重矩阵Q=10Ip，R=0.1Im，其中Im和Ip是二阶单位矩阵。

为了证明所提算法的优越性，将文中所提方法与文献[20]中提出的基于数据驱动的子空间预测控制(data-driven subspace predictive control，DDSPC)方法进行比较。先证明DDSPC算法的有效性：同时给辨识模型和实际模型相同的激励信号，将两者产生的响应进行对比，结果如图4所示。

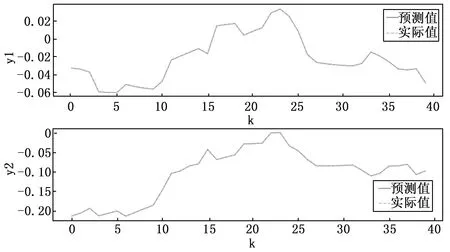
图4 DDSPC真实值和估计值响应曲线

如图4中仿真结果所示，虚线表示实际四容水箱模型在激励信号下的输出响应，实线表示根据子空间辨识得到的模型在相同激励信号下的输出响应，两条曲线重合，表示根据DDSPC方法得到的辨识模型能够精确匹配实际四容水箱系统模型。

基于DDSPC方法有效的情况下，将文中所提算法和DDSPC算法进行仿真比较，仿真结果如图5和图6所示。

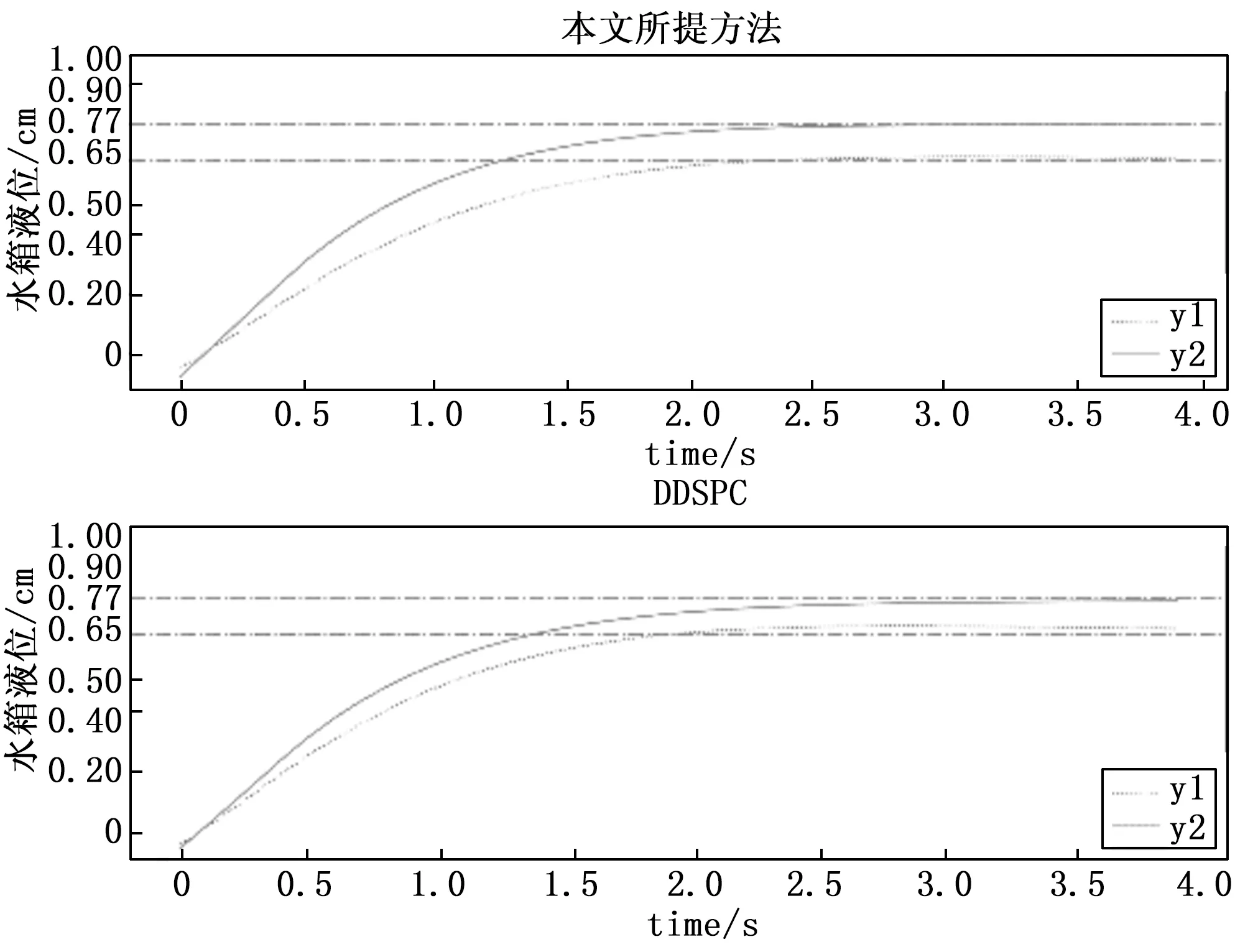
图5 本文方法与DDSPC方法跟踪控制对比

如图5和图6所示，对于四容水箱系统无噪声的情况，文中所提方法和DDSPC都有较好的控制效果，但是文中所提方法跟踪精度更高，过渡时间更短，超调量更小，具有更好的动态性能。

4.3 鲁棒性检验

为了验证改进后算法的鲁棒性，在四容水箱的每个测量输入输出数据中都添加一个大小在(-10-3，103)之间的随机高斯噪声模拟扰动，增加完噪声后的采样数据如图7所示。

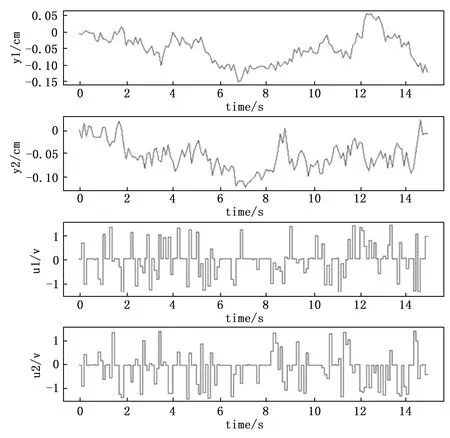
图7 含噪声的采样数据

控制器参数选择为Q=15I2，R=0.1I2，λu=λy=10-4，λα=1。参考轨迹设定值为[0 0]T，系统初始状态随机生成。为了便于观察，只展示水箱2的液位变化情况。分别比较了文中算法改进前后，改进后算法和DDSPC算法的预测输出和真实响应曲线，仿真结果如图8和图9所示。

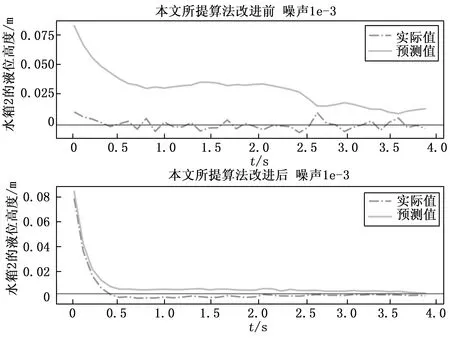
图8 噪声情况下改进前后方法对比

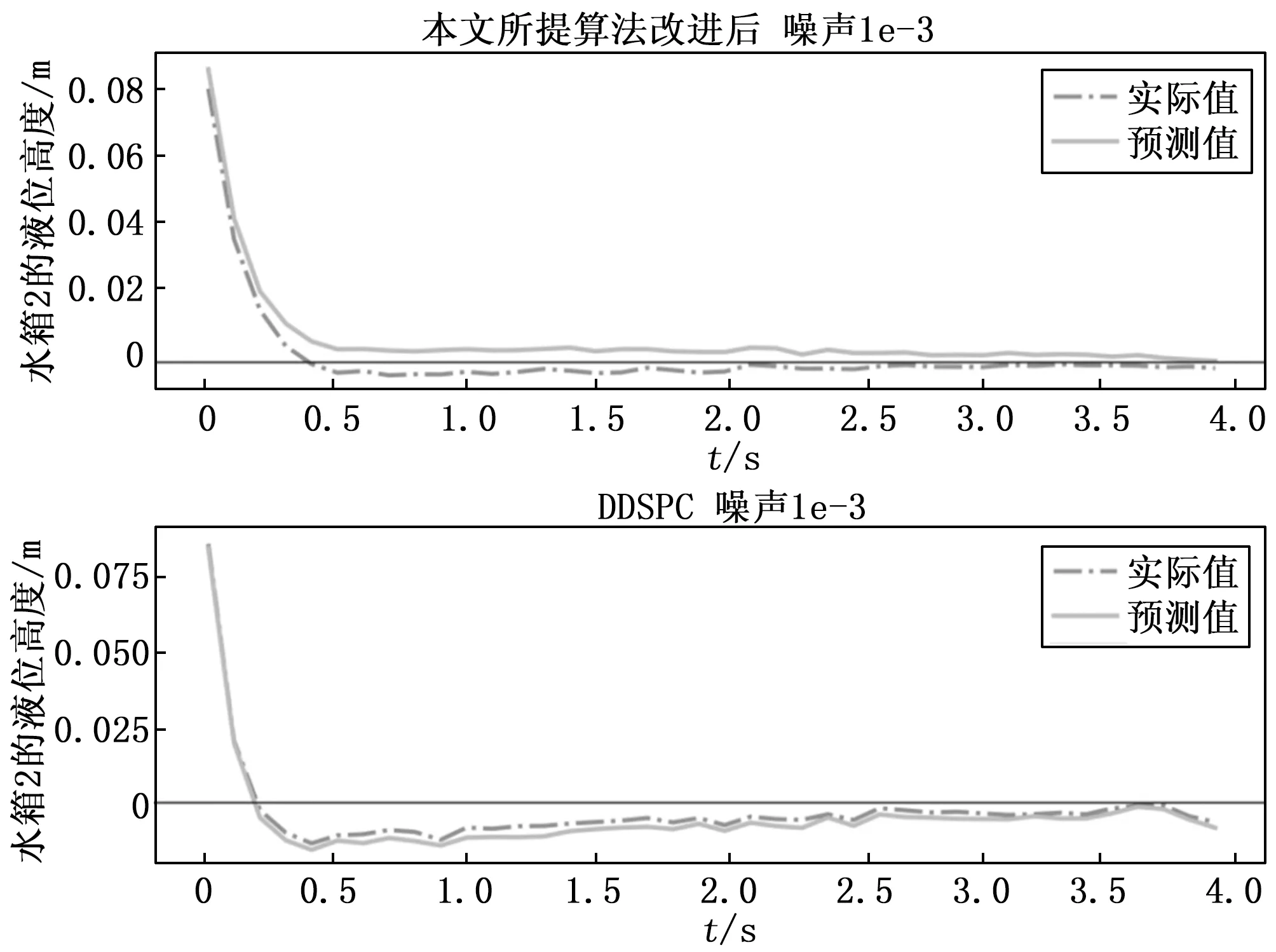
图9 本文方法与DDSPC方法对比

如图8中仿真结果所示，当系统含有测量噪声时，改进前的方案跟踪精度降低，不再能完成控制任务。引入松弛变量和L2正则项改进后，真实响应和预测值之间的偏差显著减小，跟踪效果大大增强。

如图9中仿真结果所示，与DDSPC方法相比，本文所提改进后算法跟踪精度更高，能更好的贴合参考轨迹，且系统的抖振更小。

为了进一步验证改进后算法的鲁棒性，将前述噪声扩大十倍后加入系统测量数据再进行仿真实验，控制器参数选择和之前保持一致，仿真结果如图10和11所示。

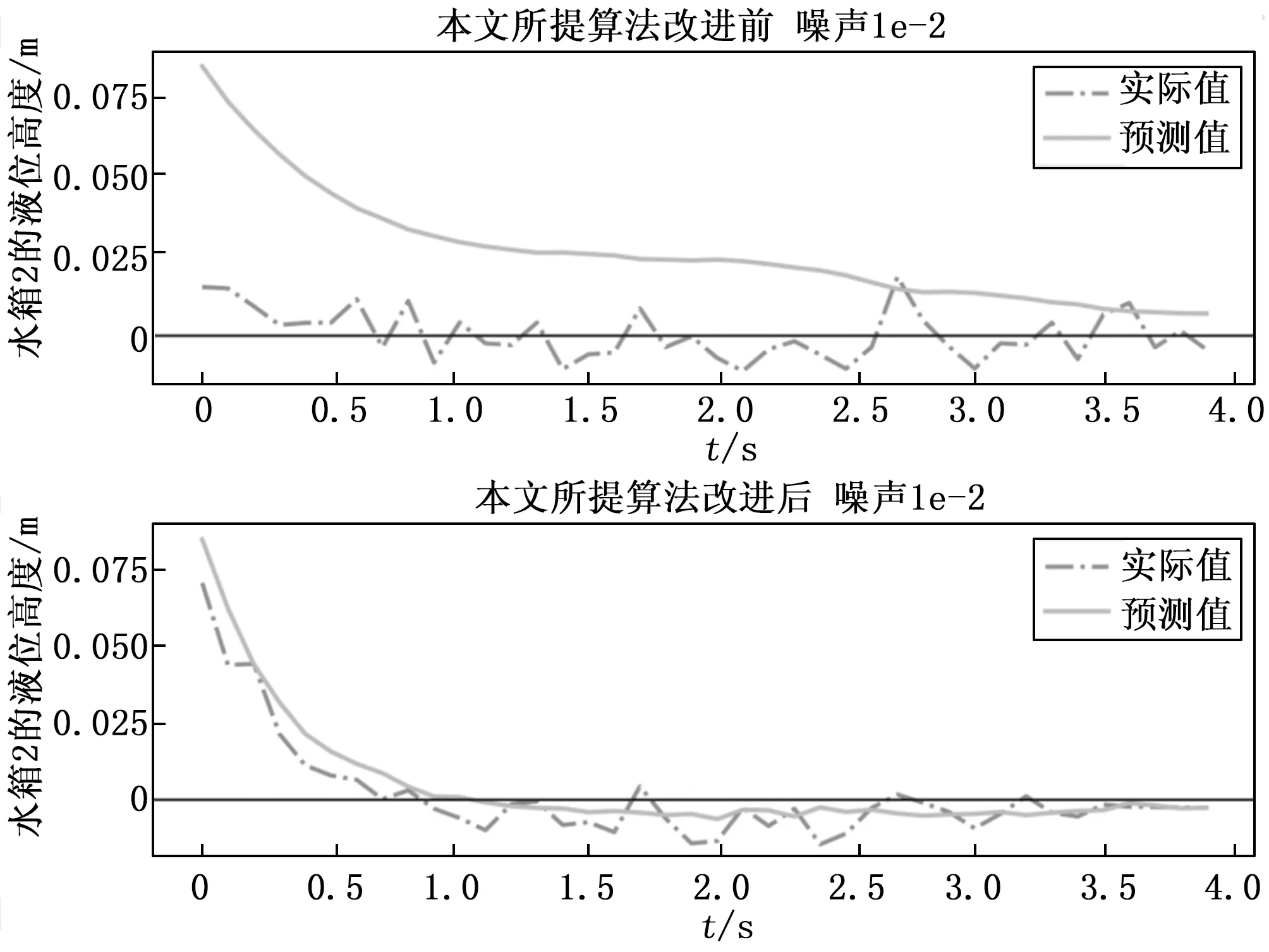
图10 噪声放大后改进前后算法对比

如图10中仿真结果所示，在将随机噪声范围扩大十倍后，改进前算法对系统的控制效果进一步变差，系统响应抖动变大，且系统无法收敛到平衡点，改进后算法有效抑制了噪声扰动，控制效果远优于改进前。如图11所示，将噪声扩大后，DDSPC算法的预测输出和实际响应产生了较大偏离，表明此时子空间预测模型和实际模型严重失配，跟踪效果进一步降低，本文所提改进后算法比DDSPC算法抗噪声扰动能力更强。为了更直观显示文中所提方法的抑制扰动能力，提出以下指标衡量抗干扰能力，其值越小表示抗干扰能力越强：

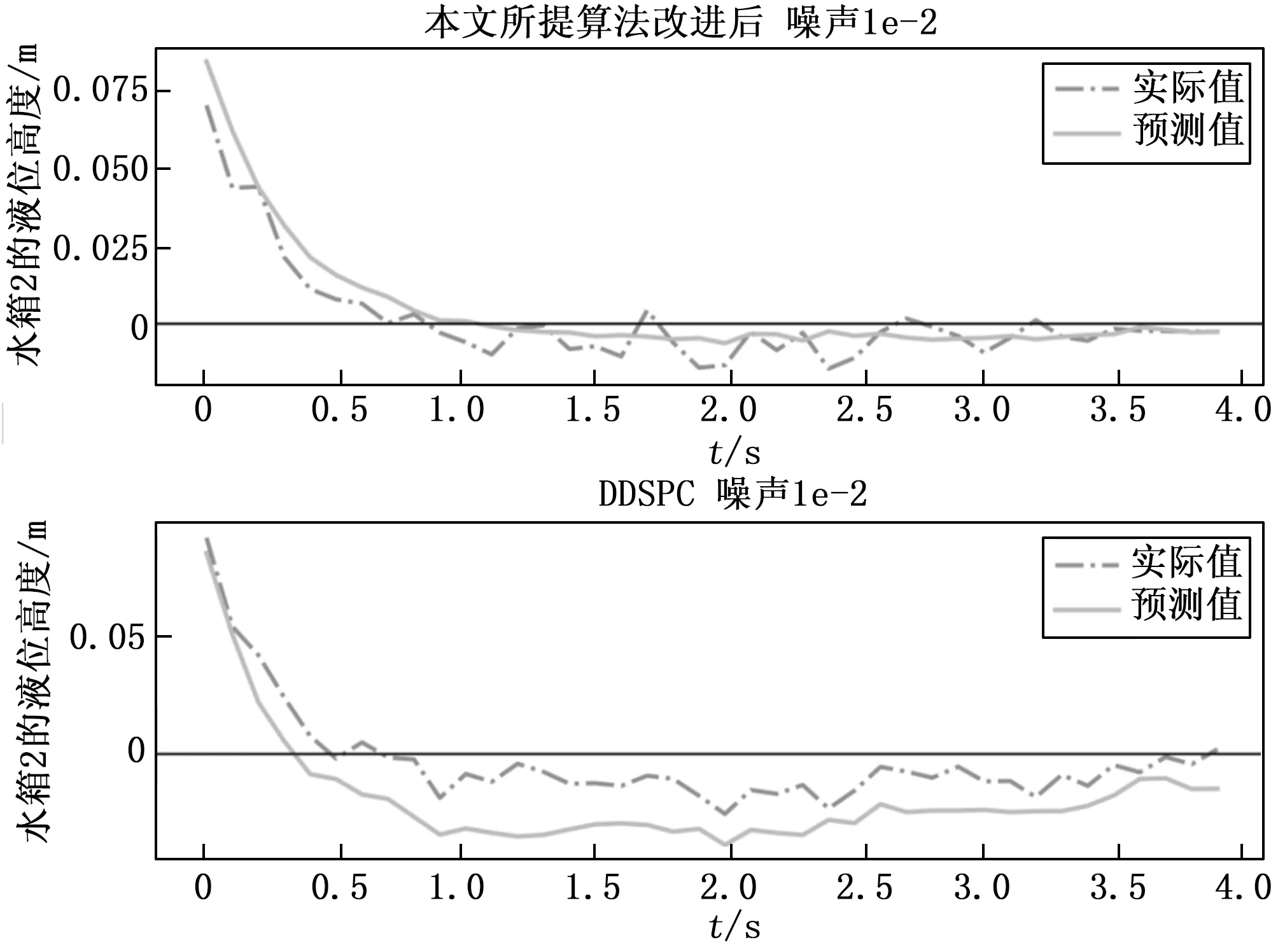
图11 噪声放大后与DDSPC算法对比

(23)

分别计算噪声为0.001和0.01时本文所提改进后算法和DDSPC算法的K值，结果如下：

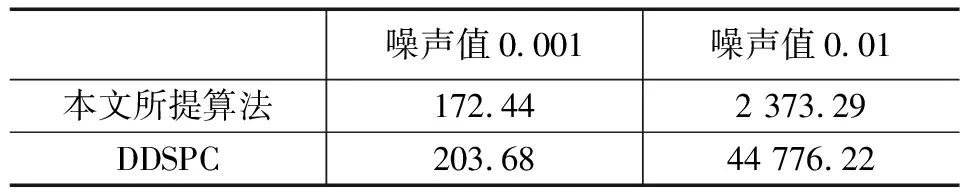
噪声值0.001噪声值0.01本文所提算法172.442 373.29DDSPC203.6844 776.22

根据上述计算的K值，在随机噪声较小时，本文所提改进后算法仅是略优于DDSPC算法，而在测量数据中含有的随机高斯噪声较大时，本文所提算法的K值仅为DDSPC算法的0.053倍，即在此指标下，本文所提算法抗干扰能力是DDSPC算法的20倍，远强于DDSPC算法。因此与DDSPC算法相比，本文所提算法在改进后具有更强的鲁棒性。

综上所述，文中所提的仅使用系统测量数据直接设计控制器的预测控制方法能有效实现对系统设定值的轨迹跟踪，具有较好的控制品质的同时也具有较强的鲁棒性。

5 结束语

本文针对测量数据中含有随机噪声的模型未知LTI系统，提出的将基于系统行为学理论的非参数模型和预测控制方法相结合的控制策略，通过直接使用系统的测量数据设计控制器解决了传统模型预测控制中预测模型设计过程复杂、精确度低且缺乏通用性的问题，同时充分考虑了有界加性高斯噪声对系统控制效果带来的影响，通过在目标函数设计和其终端约束中引入辅助松弛变量和L2正则项有效抑制了噪声带来的影响，显著提升了算法的鲁棒性。通过将该算法应用于四容水箱系统并进行仿真验证，仿真结果表明了该算法的有效性，并与同样基于数据驱动的子空间预测控制方法相比较，所提方法在具有更好动态性能的同时，抗噪声干扰能力也提升了十余倍，具有良好的控制品质和较强的鲁棒性。