基于分数阶理论的铁路基础设施形变监测数据分析与挖掘
2023-09-27封博卿蒋丽丽李聪旭杨美皓
刘 亿, 李 平, 封博卿, 蒋丽丽, 李聪旭, 王 虎, 杨美皓
(1.中国铁道科学研究院研究生部, 北京 100081;2.中国铁道科学研究院集团有限公司, 北京 100081;3.中国铁道科学研究院集团有限公司电子计算技术研究所, 北京 100081;4.综合交通大数据应用技术国家工程实验室, 北京 100081)
0 引言
铁路作为国民经济的大动脉,是国家综合交通运输体系的骨干,在经济社会发展中有着十分重要的作用。国家铁路局《2022年铁道统计公报》数据显示,截止到2022年末,全国铁路营业里程达到15.5万千米,其中高速铁路营业里程4.2万千米。由于我国幅员辽阔、疆域广大,铁路线大多横跨东西、纵贯南北,铁路在运营过程中面临着多种复杂地质、气候、自然环境考验[1]。随着北斗高精度定位技术的不断发展成熟,通过在铁路沿线隐患点布设北斗高精度定位终端,可以实现全天候毫米级的连续自动化监测,通过设置系统安全阈值,能够对铁路边坡溜坍、路基沉陷等较大形变进行快速诊断并及时预警,有效保障行车安全[2]。目前围绕铁路北斗高精度定位技术的研究工作主要集中在以下3个方面:1)通过改进北斗接收机定位算法或融合其他导航定位系统实现定位精度的提升,如戴连君[3]等人开展了基于北斗卫星载波相位平滑伪距的列车定位方法研究;严丽[4]等人提出基于北斗和GPS融合的精密定位理论。2)结合北斗高精度定位系统优势,实现与铁路业务的融合应用,如强小俊[5]等人实现北斗高精度定位技术在高速铁路桥梁的沉降形变监测中的应用;乐建炜[6]等人提出铁路编组站现场作业人员高精度定位系统。3)通过应用系统开发或对监测数据进行分析挖掘等实现北斗高精度监测数据的综合应用,如马昆[7]等人详细阐述了基于北斗定位技术的铁路基础设施监测系统的架构、功能和接口设计;朱颖[8]等人提出通过小波变换消除卫星信号中的多径误差,实现桥梁沉降量的准确预测;路志远等[9]提出利用LSTM实现对形变趋势的精准预测。目前北斗高精度定位技术已应用于京沪高铁、京张高铁、浩吉铁路、朔黄铁路等重点线路的铁路基础设施形变监测领域,为防范风险隐患、保障安全运输提供了坚实的技术支撑。
由于铁路北斗监测系统受噪声等因素影响,铁路基础设施实际位移数据会叠加±2 mm的随机噪声,因此,目前铁路北斗形变监测系统主要是通过设置系统安全阈值,在发生较大形变后再报警,属于被动管控。如何进一步通过对历史监测数据进行分析,挖掘形变演化规律,捕捉形变发育阶段的风险信息,在较大形变发生前就采取措施,从而排除列车行车风险隐患,确保铁路列车运行安全,已成为亟待解决的重要课题。传统的监测数据分析方式主要是对形变数据进行拟合,然后通过一段时间内的位移极差大小来判断基础设施形变程度,但由于受噪声等因素影响,实际监测数据会在一定区间内波动,拟合的曲线难以真实反映基础设施形变情况,另一种监测数据分析方法是对数据去噪,然后进行时间序列预测等操作来预测或判别不同隐患区风险概率,但在较小时间尺度下实际位移波动程度会远小于噪声波动程度,换言之,若通过滤波去除噪声会导致实际位移严重失真,难以保证数据分析的可靠性和准确性[10-11]。综上,由于噪声等因素导致传统数据分析方法在北斗高精度形变监测数据分析领域均难以表现出很好的效果,本文提出了利用分数阶方法分析较大时间尺度下原始数据整体趋势变化情况,挖掘隐藏在监测数据中的深层次数据特性,在数据层面判别铁路基础设施稳定状况,从而为铁路基础设施运维等相关部门提供辅助决策,实现铁路外部风险管控与隐患治理,有效保障铁路的安全运输。
1 形变监测数据分析方法
1.1 形变监测数据分析方法总体框架
基于北斗高精度定位技术的铁路基础设施形变监测系统通常布设在铁路桥梁、隧道、路基、高陡边坡等位置,用于全天候监测基础设施形变,然而这些监测位置大多处于自然条件恶劣、地质结构不稳定等区域,具有易滑坡溜坍、信号覆盖弱等特点,此外,北斗形变监测系统常受列车行驶振动、以及外部噪声等干扰,导致输出信号呈现出不同的非高斯特征,而这些非高斯特征其中就蕴含着监测区域某些特有的机理信息,本文利用分数阶分析方法对监测数据非高斯特征所反映出的不同机理信息进行分析与挖掘。分析框架见图1。
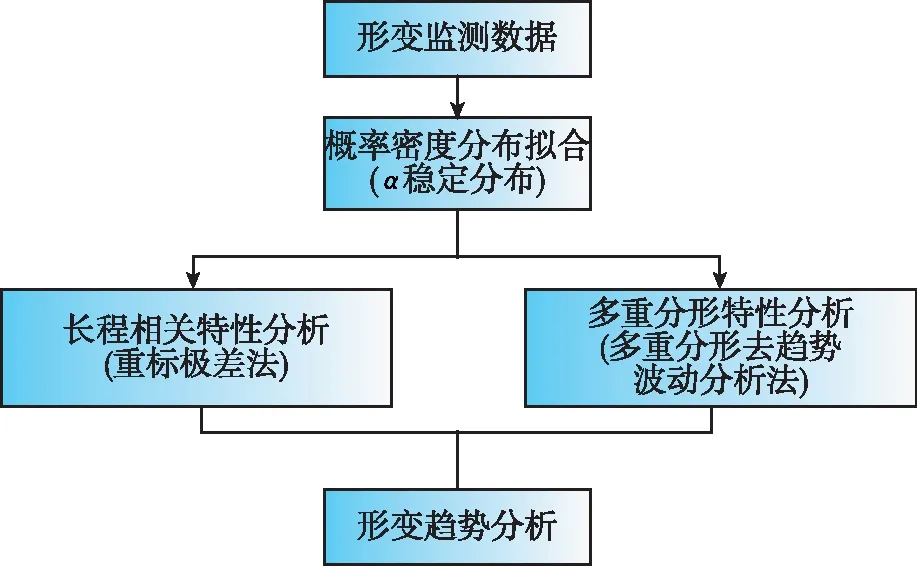
图1 铁路基础设施形变监测数据分析框架Fig.1 Analysis framework of railway infrastructure deformation monitoring data
首先利用α稳定分布对原始数据进行概率密度拟合以实现数据的非高斯特性估计,如果原始数据拟合的概率密度服从高斯分布,表示数据非高斯特征不明显,则可以采用传统方法进行分析;如果数据的概率密度不服从高斯分布,则表示数据具有非高斯特征,可以进一步通过分数阶方法对数据进行分析,从而挖掘数据在发展和演化过程中的某些相似特征与动态规律。
长程相关特性分析与多重分形特性分析是两种典型的分数阶分析方法,长程相关特性分析刻画了时序数据在较大时间尺度下的自相似性,即数据的长期趋势变化,而多重分形特性分析能通过选取不同时间标度较好地描述局部特定时间尺度下数据的不规则现象。基于此,提出利用上述分析方法分别从长期和短期两种维度挖掘数据深层次特性,以实现对监测数据的整体趋势判别,并对铁路基础设施形变所表现出的机理现象进行合理解释。
1.2 α稳定分布
铁路领域存在大量基础设施监测设备,但由于外界噪声干扰以及设备自身的不稳定性常导致输出信号概率密度分布呈现出尖峰、重尾、偏态、双峰等特征,传统高斯概率密度拟合方法已难以仅通过均值和方差两个参数来完整、准确地描述数据真实的概率密度分布情况,因此提出利用α稳定分布来对原始数据进行概率密度拟合[12-13]。α稳定分布由于没有闭环的概率密度函数,因此只能用特征函数来描述,特征函数如下
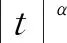
(1)
其中
在式(1)中,特征函数由α,β,γ,δ四个参数决定。参数α表示特征参数,取值范围为0<α≤2,α值越小说明尖峰特性越明显,α值越大则说明尖峰特性越不明显,当α=2时,表明概率密度完全服从高斯分布。β为偏度参数,当β等于0时,表示概率密度分布左右对称;当0<β≤1时,分布整体向左偏;当-1≤β<0时,表示分布整体向右偏。γ表示分散参数,δ表示位置参数。
1.3 长程相关特性
按时间顺序记录的数据序列是形变监测数据与其他类型数据的显著区别,因此形变监测数据会表现出持久且稳定的长期记忆特征,长程相关特性分析方法就是分析其在较大时间尺度下的长期记忆特性[14-15]。对于北斗形变监测数据X,其自相关函数可表示为
(2)
监测数据X的标度可通过功率谱定义为
f(at)≡aHf(t)
(3)
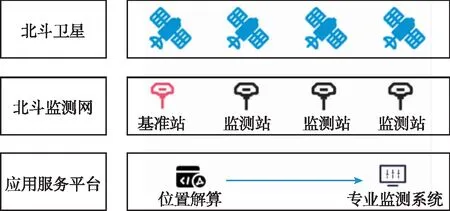
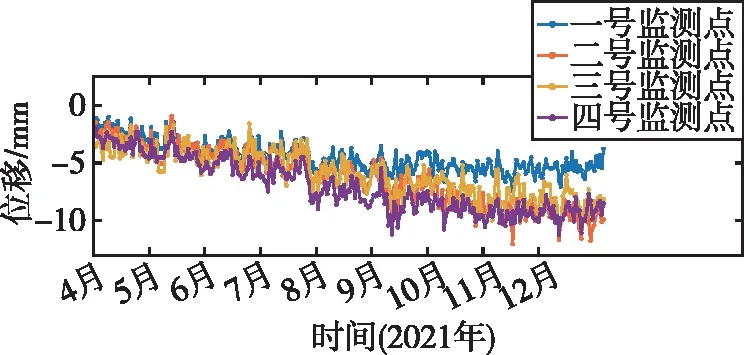
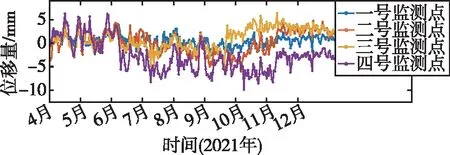
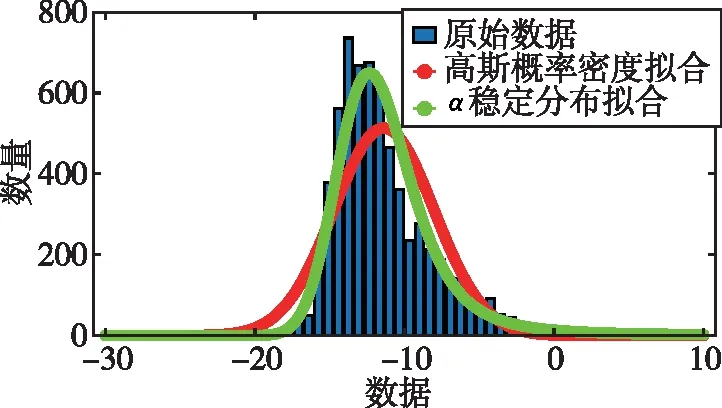
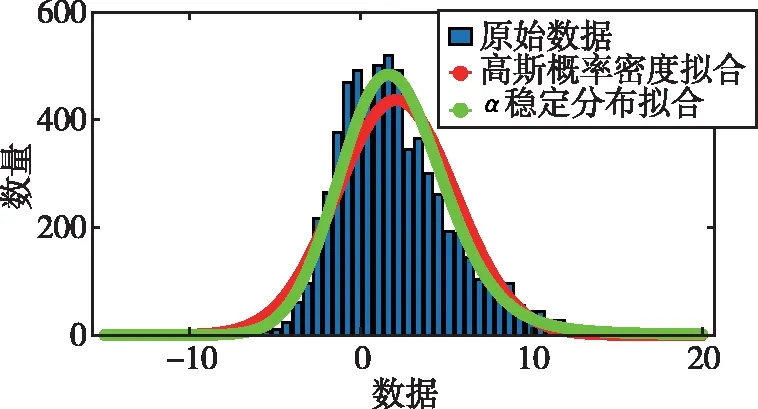
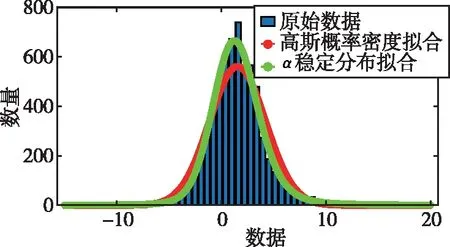
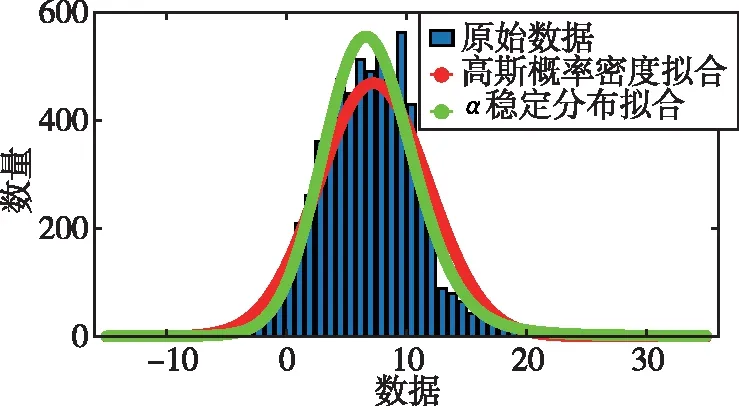
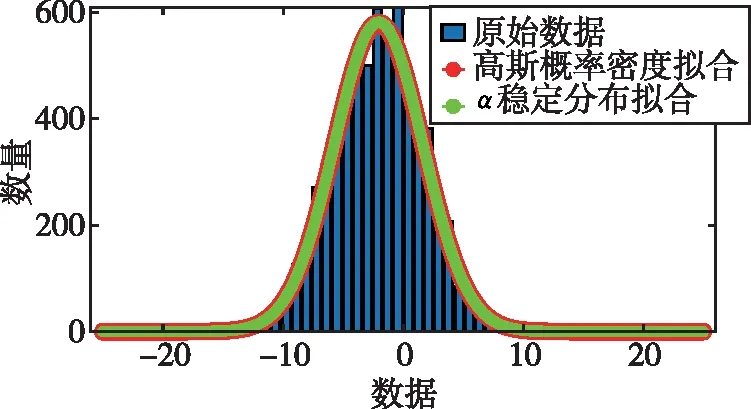
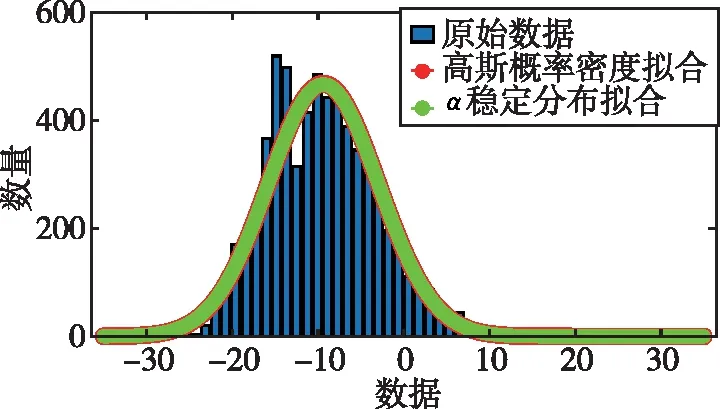
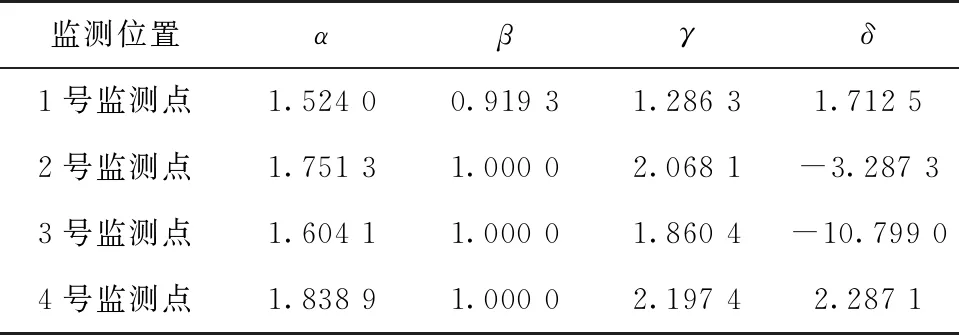
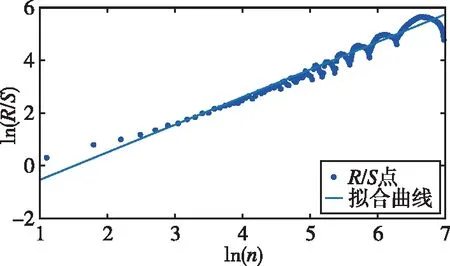
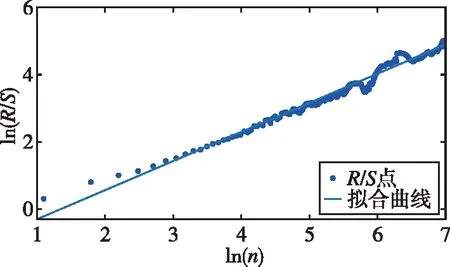
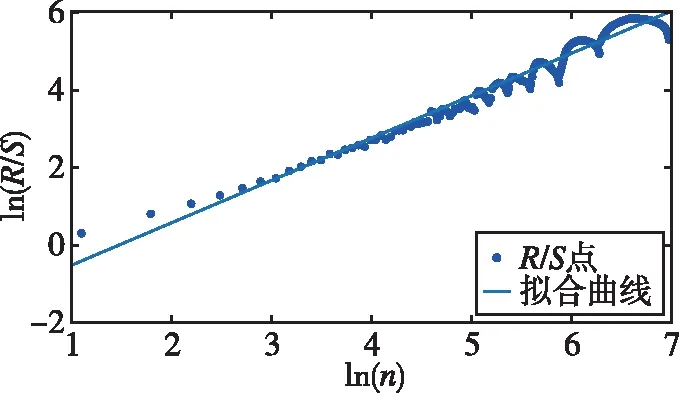
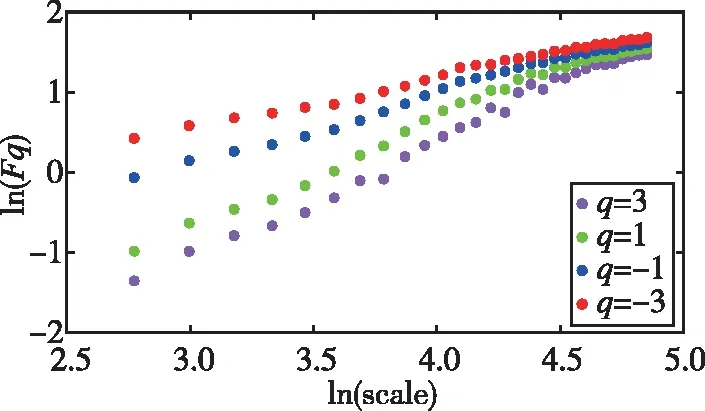
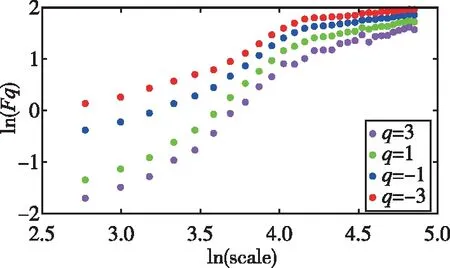
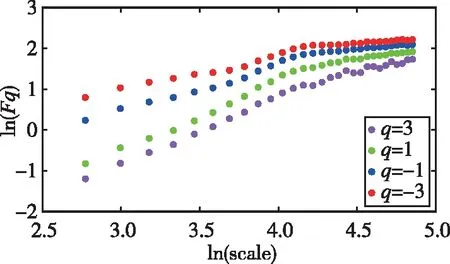
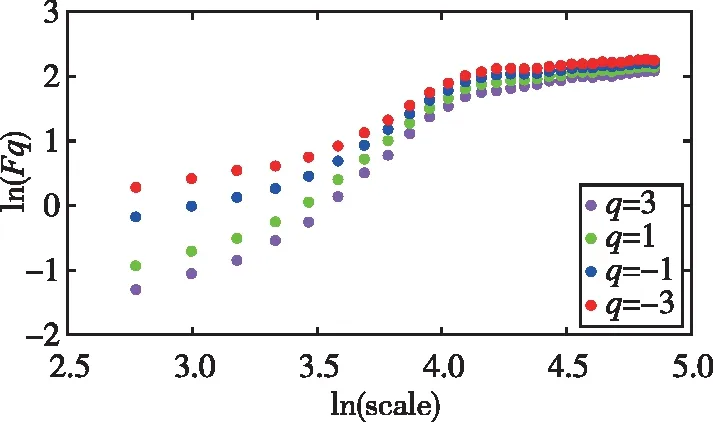
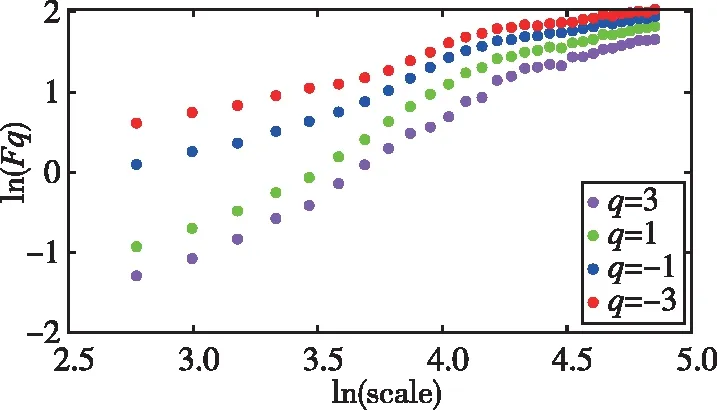
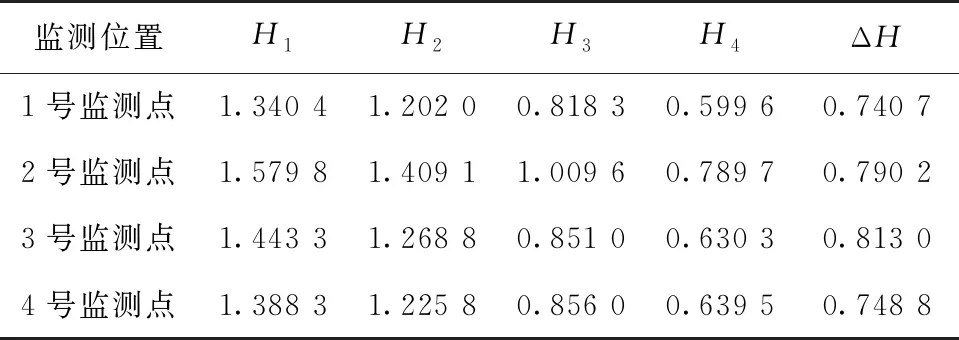
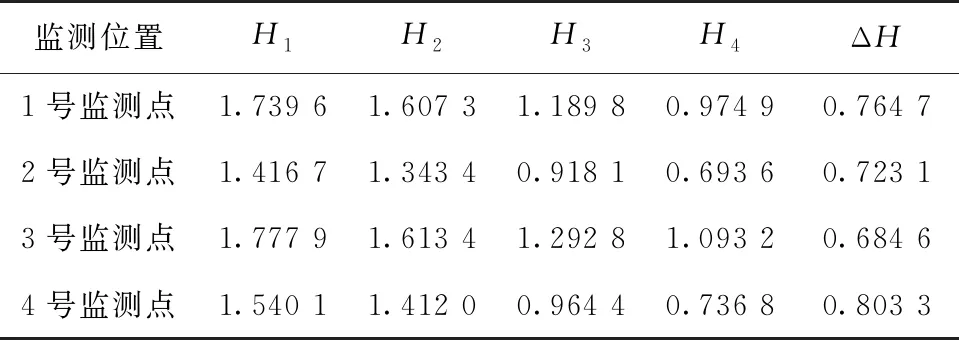
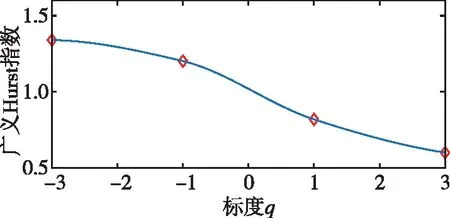
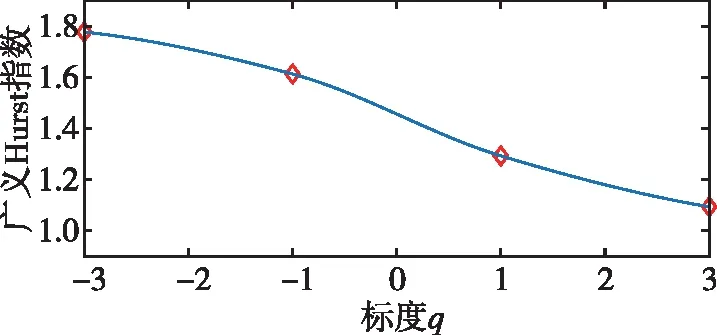
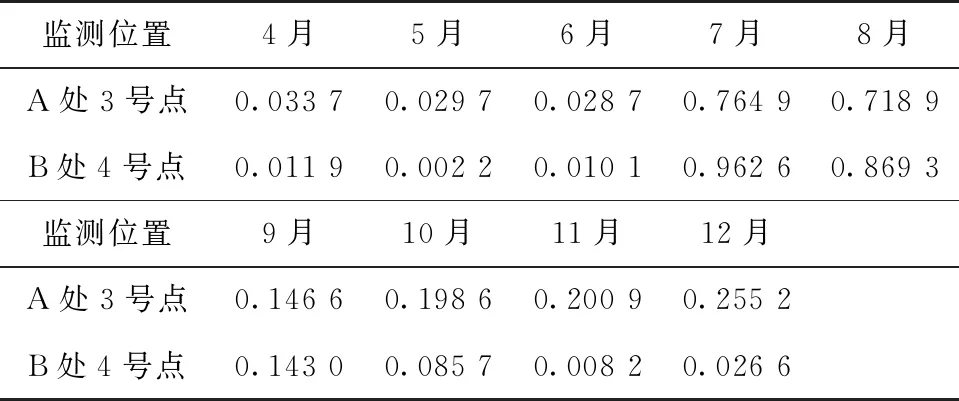
式中,H表示赫斯特指数,用于描述监测数据在较大时间尺度下的长期相关程度,取值范围为0 RXX(τ)∝τ2H-2 (4) 式中,当0 (5) (6) (7) 进而得到子序列的极差Ra以及给定区间长度n所对应的重标极差均值 Ra=max1≤j≤nYj,a-min1≤j≤nYj,a (8) (9) 逐渐扩大序列区间长度并计算对应(R/S)n,通过累计偏差与幂率得到表达式 F(τ)=(R/S)n=CτH (10) 式(10)中C表示常数,H表示赫斯特指数,对其取对数可以得到:lgF(τ)=lgC+Hlgτ,通过最小二乘法,对不同区间长度的重标极差点进行拟合,可以得到回归方程,斜率即所求赫斯特指数。 由于监测系统进行自动连续观测,因而其输出数据会在较大时间尺度下表现出长期记忆特性,即上文所述的长程相关特性。然而通过选取不同标度,分析在局部特定时间尺度下监测数据的相似特征以及分形维度,是判别数据趋势走向的另一种重要工具[16-17]。将监测数据X分成m个长度为L的子区间,分形体在该区间的概率为Pi,不同区间的Pi可用不同标度指数αi表示为 (11) 对式(11)取对数并求极限可得 (12) 式(12)中,α表示分形体某区域的分形维数,即局部分形,对式(12)乘q次并求和可得 (13) 定义q次信息维度Dq为 (14) 通过式(14)容易得出,αi的变化可以通过选取不同的标度q来实现,换言之,通过改变标度q可区分不同分形维数,进而实现时序数据的多重分形特性估计。 对于任意时间序列{Xt},计算其多重分形特性指标。首先重新构造其累计离差序列 (15) 对每个子区间v(v=1,2,…,2Ns)进行k阶最小二乘拟合,得到局部趋势函数 Yv(j)=a0+a1j+a2j2+…+akjk (16) 式中,ak表示多项式系数,k是多项式最高项次数。通过计算平均方差F2(v,s)来消除子区间v内的局部趋势。 当v=1,2,…,Ns时, (17) 当v=Ns+1,…,2Ns时, Yv(j))2 (18) 计算序列q阶波动趋势函数 (19) 在阶次q取0或2时波动趋势函数存在指数幂异常,此时Fq(s)可表示如下。 当q=0时, (20) 当q=2时, (21) 容易观察到上述波动趋势函数Fq(s)与数据长度s和分数阶次q相关,且Fq(s)随区间长度s呈幂率增加,即Fq(s)∝sHq,其中Hq即为所求的广义赫斯特指数。Fq(s)与s的幂率关系可改写为Fq(s)=AsHq,对其取对数可得 lgFq(s)=Hqlgs+lgA (22) 式中,斜率Hq表示广义赫斯特指数,是衡量监测数据长程相关特性的重要指标,其有如下结论:当选取不同标度q时,若Hq也随之变化,表明该组数据具有多重分形特性,即数据整体变化趋势不稳定,且Hq变化程度越大,数据整体变化趋势越大;若Hq不随标度q变化,表明该组数据具有单重分形特性,即数据整体变化趋势较为稳定,未来变化趋势与过去变化趋势相一致。 基于北斗导航卫星的铁路基础设施形变监测系统能够对铁路路基、边坡、桥梁等进行毫米级连续自动化监测,可显著提升铁路工程监测能力。铁路基础设施形变监测系统由北斗卫星、北斗监测网、应用服务平台三部分组成,其组成架构如图2所示,通过在风险隐患区布设北斗监测网,可以实现对北斗卫星信号的连续观测、接收、并加密传输到应用服务平台,应用服务平台对北斗信号进行解算得到位移形变信息,得到的毫米级形变位移信息则通过专业算法进行汇集应用,最终展示在专业监测系统终端,用于辅助安全决策。 为防范重大风险隐患,保障安全运输,铁路部门在某铁路沿线高陡边坡、路基、隧道、桥梁等处风险隐患区布设北斗监测设备。选取典型高陡边坡A和特殊地段路基B两处风险隐患区进行实测数据分析,两处风险隐患区地处陕北黄土高原,生态环境相对恶劣,加之极端气候频现,易造成滑坡、泥流泛滥等自然灾害,此外,由于铁路部门为保障列车运行安全严格限制上道作业时间,因此提出利用北斗高精度定位系统实现对铁路沿线基础设施进行全天候连续自动化监测。A、B两处风险隐患区形变监测系统基准站与监测站之间最大距离为 300 m,各监测点均匀分布在铁路沿线两侧。此外,北斗形变监测系统采用通用高精度静态基线解算程序。选取A、B两处风险隐患区共8个监测点进行实测数据分析,时间跨度为2021年4月1日至2021年12月31日,数据采集频率是10 m 1个历元,一个解算周期为1 h,剔除异常数据后,每组共计6 485个数据。 图2 铁路基础设施形变监测系统架构Fig.2 Framework of railway infrastructure deformation monitoring system 图3(a)为A处高陡边坡监测数据时序图,从图中可以观察到4组监测数据变化平稳,但均有缓慢衰减趋势,且在2021年8月之后,4组数据的一致性逐渐减弱,数据走势表现出较为明显的差异。图3(b)为B处路基监测时序图,从图中可以观察到数据变化并不平稳,且在2021年6月之后,4组数据变化剧烈,数据走势也明显不同,从时序图中难以直接观察出数据的趋势特性,更无法从中判别监测区域的稳定性情况。 (a) A处高陡边坡监测时序图 (b) B处路基监测时序图图3 形变监测数据时序图Fig.3 Time series diagram of deformation monitoring data 图4和图5分别为A处高陡边坡和B处路基监测数据的概率密度拟合图,其中蓝色柱状表示原始数据的概率密度分布,红色表示传统高斯概率密度拟合,绿色表示α稳定分布拟合。表1和表2分别为A处高陡边坡和B处路基的α稳定分布拟合参数值。从拟合效果来看,α稳定分布拟合相较于传统高斯概率密度拟合能更好地描述数据真实的概率密度分布,并能通过拟合参数直接判断数据的偏度、离散度等信息。从拟合结果来看,各组数据并未出现严重拖尾现象,说明数据是在一个固定区间内游走,但是变化过程并不平稳,仍表现出偏态、双峰等特殊分布状况,表1和表2中除B处4号监测点外,参数α值均不等于2,进一步验证监测数据中广泛存在的非高斯特征。 (b) A处2号监测点 (c) A处3号监测点 (d) A处4号监测点图4 A处高陡边坡监测点概率密度分布拟合Fig.4 Probability density distribution fitting of the data of monitoring points in risk area A (a) B处1号监测点 (b) B处2号监测点 (c) B处3号监测点 (d) B处4号监测点图5 B处路基监测点概率密度分布拟合Fig.5 Probability density distribution fitting of the data of monitoring points in risk area B 从时序图和概率密度拟合图来看,不同隐患点的数据趋势、离散情况明显不同,即使是同一隐患点,不同组数据的概率密度分布也呈现出巨大差异,其原因在于监测设备独立放置于室外,无其他变量与其耦合,噪声干扰和设备所在区域物理特性是影响监测数据统计特性出现差异的主要因素。因此将进一步利用分数阶分析方法对形变监测数据统计特性差异所反映出的不同物理机理信息进行挖掘。 表1 A处高陡边坡统计分析 表2 B处路基统计分析 本节进一步利用分数阶方法挖掘形变监测数据在较大时间尺度下的长期记忆特性,图6和图7分别为A处高陡边坡和B处路基监测数据的赫斯特指数拟合图,图中横坐标表示选取的区间标度,纵坐标表示标度所对应的重标极差数值,而圆点表示计算的重标极差点,直线则是根据不同区间长度下的重标极差点的最小二乘拟合而得,其斜率表示赫斯特指数,表3详细记录了赫斯特指数数值的大小。 (a) A处1号监测点 (b) A处2号监测点 (c) A处3号监测点 (d) A处4号监测点图6 A处高陡边坡各监测点赫斯特指数拟合Fig.6 Hurst exponent fitting of the data of monitoring points in risk area A (a) B处1号监测点 (b) B处2号监测点 (c) B处3号监测点 (d) B处4号监测点图7 B处路基监测点赫斯特指数拟合Fig.7 Hurst exponent fitting of the data of monitoring points in risk area B 从图中可以看出随着标度n的增大,重标极差点增多,且重标极差点与标度n呈正相关,表3中各监测点赫斯特指数均大于0.5,表明数据在较大时间尺度下表现出较为明显的长程相关特性,即监测数据未来变化趋势与过去变化趋势相同。此外,由于标度不同,重标极差点并不均匀分布,导致在最小二乘拟合时,赫斯特指数与理论值稍有出入。 表3 A、B隐患区各监测点赫斯特指数数值 上节通过对形变监测数据的长程相关性进行分析,表明形变监测数据在较大时间尺度下存在长期记忆特性,本节将对数据的多重分形特性做进一步分析。图8和图9分别为A处高陡边坡和B处路基监测数据的广义赫斯特指数拟合图,图中4种颜色的圆点表示4种标度下的波动离散点,同一种颜色圆点通过最小二乘法拟合得到的斜率就表示这组数据在该标度下的广义赫斯特指数,而4组标度下广义赫斯特指数的极差就可以衡量这组数据的多重分形特性程度。表4和表5中的H1,H2,H3,H4分别表示4种标度下拟合的广义赫斯特指数,而ΔH表示不同标度下广义赫斯特指数的极差。表6是两处风险隐患区2021年度真实位移形变量,图10和图11则是根据各组数据广义赫斯特指数拟合而得的保形曲线。 图8是A处高陡边坡的广义赫斯特指数拟合图,从图中可以观察到每组数据在不同标度下波动离散点的走势存在显著差异,这说明其多重分形特性较为明显。表4中详细列出了拟合的广义赫斯特指数,并给出每组数据在不同标度下广义赫斯特指数的极差ΔH。从表中可以看出ΔH大小依次为3号、2号、4号、1号监测点,这说明1号监测点的多重分形特性最弱,即数据整体趋势较为稳定,从时序图上也可以印证该组变量变化过程相对更为平缓,3号监测点的ΔH最大,表明该组变量分形特性最明显,数据整体趋势更不平稳,对于同一风险隐患区同一种型号设备来说,其所遭受的外界噪声干扰更大,即所处的监测位置地质更加不稳定,潜在安全隐患更大。 (a) A处1号监测点 (b) A处2号监测点 (c) A处3号监测点 (d) A处4号监测点图8 A处高陡边坡各监测点广义赫斯特指数拟合Fig.8 Generalized Hurst exponent fitting of the data of monitoring points in risk area A (a) B处1号监测点 (b) B处2号监测点 (c) B处3号监测点 (d)B处4号监测点图9 B处路基各监测点广义赫斯特指数拟合Fig.9 Generalized Hurst exponent fitting of the data of monitoring points at risk area B 表4 A处高陡边坡广义赫斯特指数拟合参数 表5 B处路基广义赫斯特指数拟合参数 表6 A、B风险隐患区真实沉降形变量 图9是B处路基的广义赫斯特指数拟合图,表5是拟合的广义赫斯特指数。图9中各组数据的波动离散点走势不同,说明B处路基隐患点的各组变量也存在较为明显多重分形特性,表5中ΔH大小依次为4号、1号、2号、3号监测点,这说明4号监测点的分形特性最明显,即数据整体趋势更不平稳,而3号监测点的多重分形特性最弱,即数据整体趋势较为稳定,这其中隐含的物理机理为3号监测设备所处位置的风险隐患更大。通过MFDFA算法得出不同区域不同监测位置ΔH大小顺序与对应区域2021年度监测位置的实际位移形变大小相吻合,进一步验证了本方法的有效性与可靠性。此外,图10和图11所示的保形曲线趋势过渡平滑,标度内无极值,说明各组变量即使存在不同程度的多重分形特性,也并未出现因数据急剧变化而导致的标度大小和波动离散点趋势不一致现象,即说明数据在演化过程中总体变化趋势上是相对稳定的。 (a) A处1号监测点 (b) A处2号监测点 (c) A处3号监测点 (d)A处4号监测点图10 A处高陡边坡监测点广义赫斯特指数保形曲线Fig.10 Conformal curve for generalized Hurst exponent of monitoring data in risk area A (a) B处1号监测点 (b) B处2号监测点 (c) B处3号监测点 (d) B处4号监测点图11 B处路基监测点广义赫斯特指数保形曲线Fig.11 Conformal curve for generalized Hurst exponent of monitoring data in risk area B 上述实验表明,通过多重分形特性分析能够准确地判别出各组北斗监测数据从2021年4月到12月整体的分形特性程度。为探究监测数据每月的多重分形特性程度,分析每月数据的平稳状况,论文选取稳定性较差的A处3号监测点和B处4号监测点做进一步详细分析。图12是A处3号监测点4月到12月逐月的ΔH,图13是B处4号监测点4月到12月逐月的ΔH。表7是A处3号监测点和B处4号监测点各月份ΔH的详细拟合参数。 从图12中可以看出,A处3号监测点7、8月的ΔH最大,说明这两个月的分形特性最为明显,4、5、6月份ΔH相对较小,而9,10,11,12月份ΔH有缓慢上升的趋势,这说明这4个月的多重分形特性更加明显,表7中拟合参数ΔH的值进一步验证上述结论。从图13中可以看出,B处4号监测点7月、8月的ΔH也是相对较大,而其他月份并未出现缓慢上升或下降的趋势,这说明该监测点其他月份数据的变化趋势相对平稳。 图12 A处高陡边坡3号监测点ΔHFig.12 Monthly ΔH of monitoring point No.3 in risk area A 图13 B处路基4号监测点ΔHFig.13 Monthly ΔH of monitoring point No.4 at risk area B 表7 监测点月度ΔH 首先利用α稳定分布对原始数据进行概率密度拟合,从各组数据拟合参数来看,A处高陡边坡α值更小一些,这说明外界噪声对该隐患区的干扰程度更强,即该风险隐患区监测数据的演化过程相较于B处路基更不平稳。从长程相关特性角度来看,各组数据拟合的赫斯特指数都非常接近1,这说明在较大时间尺度下数据相关程度非常高,但由于拟合的赫斯特指数都非常接近,难以判别各组数据的趋势变化强弱,因此本文又对各组数据的多重分形特性进行分析。从实验结果来看,多重分形特性分析能够对各组变量的稳定性程度进行精准判别,实验表明A处3号监测点的分形特性最弱,数据变化趋势最为平稳,即稳定性最强,从时序图上也可以印证该组数据变化过程最为平缓。对于B处路基隐患区,拟合数值表明4号监测点的分形特性最强,这表明该组数据变化过程最为剧烈,隐含的地质信息更为不稳定。 从各组监测数据的ΔH来看,A处高陡边坡普遍大于B处路基,这说明A处高陡边坡的多重分形更为明显,即该处隐患区的稳定性更弱、安全风险更高。此外,从拟合的保形曲线来看,虽然各组数据在不同程度上表现出稳定性差异,但曲线过渡平滑,均未出现因数据急剧变化而导致的标度大小和波动离散点趋势不一致现象,即说明数据总体变化趋势是相对稳定的,这一点可以从拟合的概率密度分布并未出现拖尾以及时序图发展演化过程相对平稳得到印证。本文还进一步对稳定性较弱的A处3号监测点和B处4号监测点进行每月的多重分形特性分析,研究发现上述两处监测点7月、8月的多重分形特性较其他月份更为明显。结合实际分析可知,夏季雨水足、土质较为疏松,降低了不良地质体的稳定性,因此在监测数据上就表现更为明显的多重分形特性。 本实验选取铁路基础设施形变实测数据进行分析,虽然未得到严密平差后的结果来做进一步综合比较,但由于北斗高精度定位技术已较为成熟,且A、B风险隐患区的北斗高精度定位终端运行稳定,因此本实验数据能够反映基础设施的真实形变情况。通过对实测数据做统计特性分析、长程相关特性分析以及分形特性分析,有效挖掘了实际监测数据中存在的尖峰重尾特性、长程相关特性以及多重分形特性,精准判别了不同时间尺度下各监测数据的趋势变化以及稳定性情况,实验结论与2021年度对应区域监测位置的实际位移形变大小相吻合,实验结果能够为铁路基础设施运维等相关部门提供相应辅助决策。 文中所提出的分数阶分析方法通过对监测数据趋势信息进行挖掘,可有效进行噪声干扰下北斗形变监测数据的精准分析,所提方法能有效捕捉到隐患区的风险信息,能够为保障行车安全提供重要的决策辅助支撑。 1)通过直接对原始数据进行分析,能充分挖掘监测数据在发展演化过程中的趋势信息,有效判别隐患区风险信息;各组监测数据均存在显著的非高斯特性,且在较大时间尺度下存在显著的长程相关特性与多重分形特性。 2)各监测点虽呈现出不同程度的稳定性差异,但监测数据分布均匀,数据变化趋势总体相对稳定;A处高陡边坡的稳定性总体弱于B处路基,且A处3号、B处4号监测点稳定性更弱,隐患区7月、8月的地质稳定性弱于其他月份。 3)本研究方法分别对监测数据进行了统计特性分析、长程相关特性分析以及多重分形特性分析,未来将进一步考虑将3种分析方法融合,实现铁路基础设施形变的综合定量评估。
1.4 多重分形特性

2 实测分析
2.1 数据源
2.2 统计特性分析

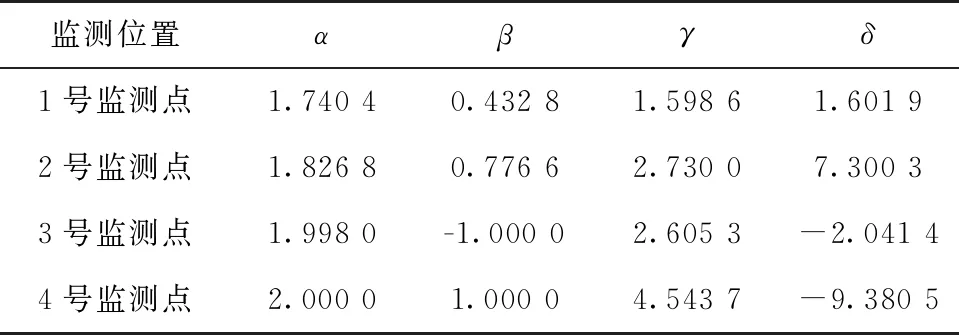
2.3 长程相关特性分析
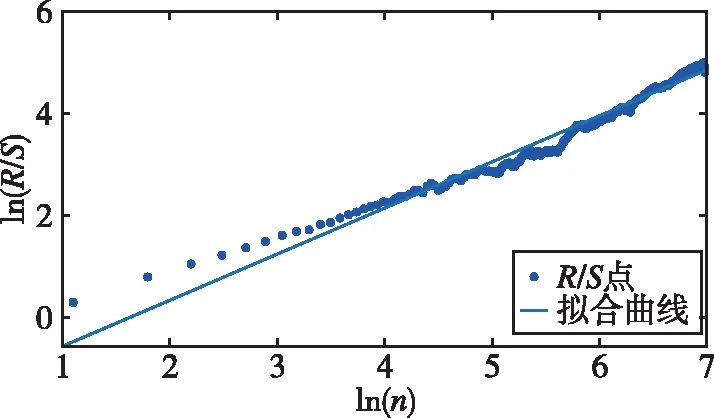
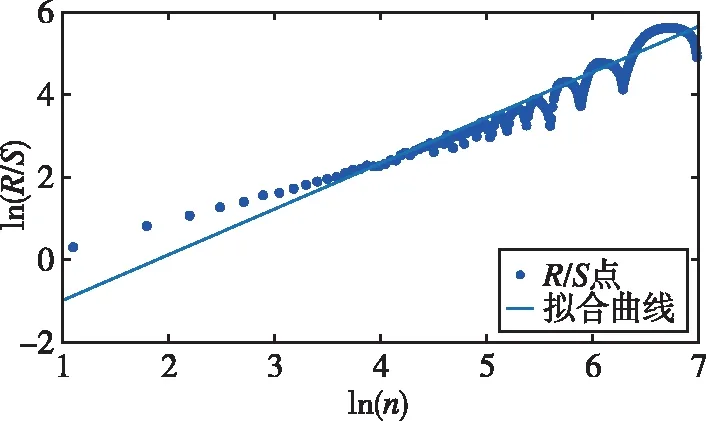
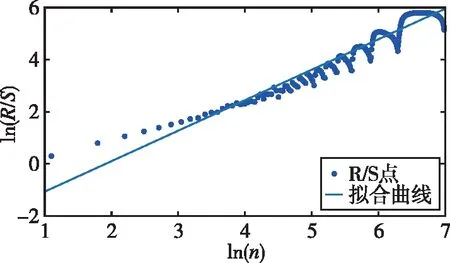



2.4 多重分形特性分析

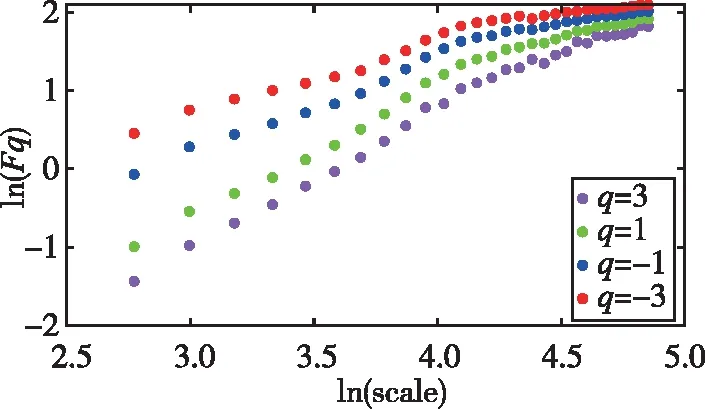



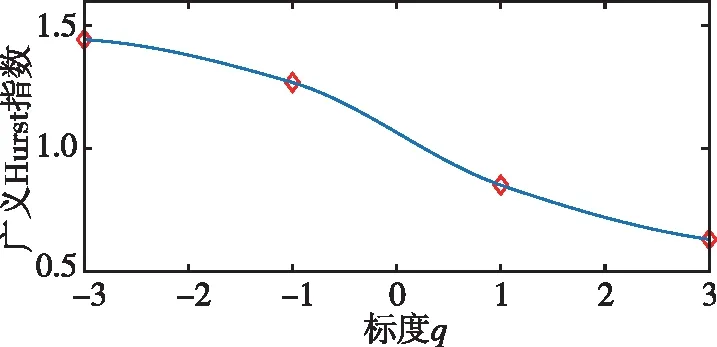
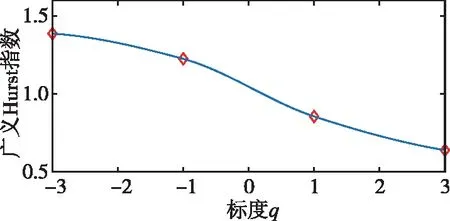
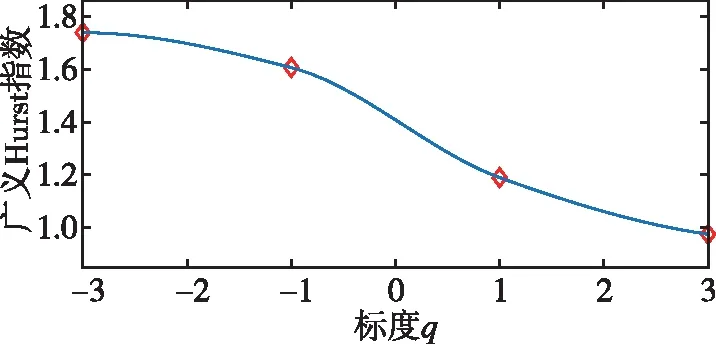
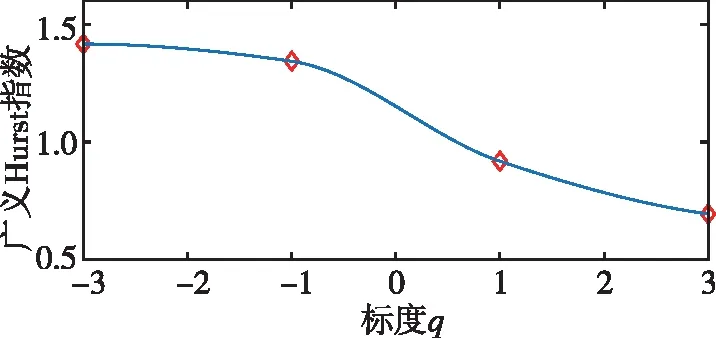



2.5 结果分析
3 总结与展望
