基于随钻振动信号与深度学习的岩性智能预测方法

王 胜，赖 昆，张 拯，柏 君，罗中斌，李冰乐，张 洁

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

地质勘探中，钻探取心是获取地表下准确的地质资料的重要方法之一。对岩心进行分析可得知其颜色、成分、结构、胶结物、胶结类型、特殊矿物等特征，从而判断地层岩性。然而，传统的岩性识别方法如岩屑录井、岩心录井和钻后测井资料的解释与处理等都存在一些不足，例如岩屑测井具有滞后性、处理钻后测井资料无及时性等。因此，为了快速实时地识别岩性，国内外的研究人员进行了大量的研究[1-2]。

钻进过程是一个比较复杂的岩石破碎过程，而钻进不同地层或钻机处于不同工况下，钻机以及整个钻柱系统会产生各种响应。经系统研究后，研究人员发现岩石物理和力学性质以及处于的水环境等都会使钻进过程中振动、声音信号的响应特征发生变化[3-5]。研究表明，井下钻具振动信号产生的高低频可表征不同的物理意义，低频段反馈钻具工作状态，高频段反馈岩性特点，因此可以用于地层岩性识别。一些学者通过分析钻进过程中的钻进参数和随钻信号与岩石的响应关系[6-8]，如观测并分析随钻碎岩加速度[9]，以及进行室内钻进实验[10-11]，对声振信号的时域、频率和时频谱进行分析和解释，得到每类岩性与振动、声音信号之间的特定关系，揭示其钻柱振动频谱特性，研究者认为，通过调查和分析不同岩石的频率行为，可以检测到岩石类型。

随着图像处理技术和深度学习技术的快速发展，岩性智能识别方法正在成为可能。深度学习技术在图像和声音识别技术方面得到了广泛应用，其中卷积神经网络在图像处理方面的研究尤为深入[12]，如牛津大学计算机视觉组(Visual Geometry Group)和Google DeepMind 公司研发了VGGNet 卷积神经网络[13]，多伦多大学设计的AlexNet 网络[14]，这2 个模型在大规模视觉识别挑战赛取得优异成绩。随后，越来越多的学者开始利用机器学习进行岩性智能预测和岩体质量等级预测[15]等研究。在岩石图像方面，一些学者直接采集岩石图像建立岩性自动分类方法[16-19]，或者基于岩石薄片图像建立卷积神经网络模型[20]，该模型自动提取图像特征并建立分类器进行自动分类。此外，还有学者通过采集随钻声振信号，并提取特征图像，以此建立岩性智能识别模型。他们设计实验收集钻进过程中的振动信号，分析提取代表岩性的特征，利用深度卷积网络的高效计算能力，结合振动信号实时采集的优势，处理复杂的非结构化数据，建立岩性识别模型，实现高效的岩性识别分析[21-22]。

综上，岩性的智能识别能够减少主观人为判断的失误、提高识别精度及效率，但通过直接采集的岩石或岩心图像，会因为采集设备精度、角度等造成误差，导致智能识别困难。而在岩石钻孔过程中，钻头和钻具直接与地层岩体相接触，在此过程中产生的振动信号中蕴含着丰富的岩性信息，并且在近钻头位置处，振动的产生主要来自钻头与岩石的相互碰撞摩擦产生的频率宽泛的振动波。笔者采集岩石振动信号，并将信号预处理构建为数据集，探讨振动信号与钻头此时所钻岩体之间的响应关系，提出基于VGG11 网络的岩性预测模型，以期为岩性智能预测提供新的解决方案，同时为钻进过程中实时预测岩性提供参考和借鉴。

1 方法原理

1.1 总体构架

设计室内微钻实验方案，选取7 种岩石，通过三轴振动加速度传感器采集钻进过程中的振动信号；用信号处理方法对振动信号滤波、降噪，并进行时频域分析生成时频特征RGB 图像，建立数据集；传统的岩性预测模型基于测井数据，针对此类模型存在数据采集滞后、特征提取复杂、解释受限等缺点，构建了深度学习中VGG11 网络为基础的随钻岩性实时预测模型，对图像进行特征提取，确定振动信号特征对应的影响因素，完成模型训练、调优、评估等迭代流程，实现对图像的分类，最后对岩性预测模型验证。基于随钻振动信号的岩性预测总体方案如图1 所示。

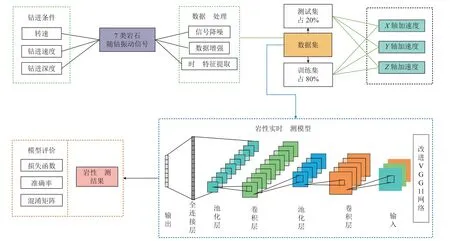
图1 基于随钻振动信号的岩性预测总体方案Fig.1 Overall scheme of lithology prediction based on vibration signal while drilling

1.2 信号处理及模型构建

采集的原始数据是关于时间变化的随钻振动信号，即时域信号，表征较为形象与直观，使用离散傅里叶变换(DFT，Discrete Fourier Transform)将时域信号转换为频域信号，在频域上进行分析则更为简洁，剖析问题会更加深刻和方便，在进行变换时需注意频域混叠，只有当采集卡的采样频率大于传感器响应频率两倍时，才能避免混叠。在计算机中需使用快速傅里叶变换(FFT，Fast Fourier Transform；计算机使用DFT 高效、快速的计算形式)。频域信号通过下式进行变换：

式中：Y(n)为一个长度为K的有限长离散频率序列，n=0,1,···,K-1,Hz；y(t)为一段时间T的有限长离散时间序列，可为复信号，t=0,1,···,K-1,s；j 为虚数单位。

通过短时傅里叶变换(STFT，Short Time Fourier Transform)将振动信号数据的时域、频域图生成时频图，时频图能体现信号在不同时间、不同频率的能量大小，即能够直接明了表征信号的频率关于时间的变化关系，同时也有对应时间频率的能量变化，横轴为时间，纵轴为频率，二维图中用颜色表示能量大小，而在三维图中用信号的起伏波动来表示能量变化，图2 表示时频图维度转换。

图2 时频图维度转换Fig.2 Dimension conversion of time-frequency image

变换的关键在于加窗，对于窗的选取必须考虑大小，窗选得窄，窗内信号短，频率分辨率低；窗选得宽，窗内时间信号长，导致时间信号分辨率低。

深度学习模型选择卷积神经网络(CNN，Convolutional Neural Networks)进行构建，相较于传统的人工神经网络，卷积神经网络的局部连接和参数共享等机制使得图像特征提取的利用率提高，网络结构的参数大幅减小，可以训练出更好的模型，且能有效避免过拟合现象。卷积神经网络包含卷积层、池化层和全连接层。卷积层不需展开，使用同一个卷积核去进行计算，所需参数就取决于卷积核的大小和数量，卷积操作时平移图像不会影响识别。池化层对图像进一步提取更高维的特征，再次减小所需参数量，去掉多余信息，提高神经网络模型运算速率和泛化能力。在特征提取完成之后，需要用全连接层来完成分类任务，通过Softmax 分类器，得到不同种类的概率分布问题。

1.3 模型评估标准

岩性的实时预测属于模式识别范畴，是多分类任务中的一种。使用的评价指标有准确率A(Accuracy)、精确率P(Precision)、召回率R(Recall)和F1值(FMeasure)。根据真实结果与预测结果对应关系，可将每张图像划分为真正例PT、假正例PF、真反例NT和假反例NF4 个类别，4 种具体关系见表1。

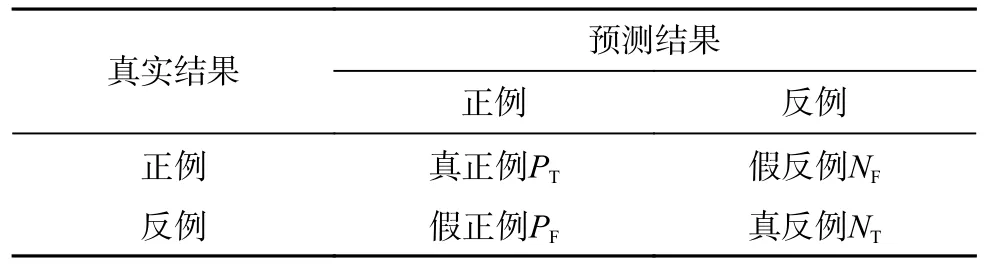
表1 岩性分类混淆矩阵Table 1 Lithology classification confusion matrix

准确率是最为常见的评价指标之一，即正确分类的图像占测试集的比例。通常认为准确率越高，模型的效果就越好。计算如下式：

精确率也称为查准率，即预测为正例的数据中，实际也为正例的比例。计算如下式：

召回率也称为查全率，是测试集中有多少个正例被正确预测的度量指标。计算如下式：

F1是精确率与召回率的调和平均，F1越大，模型的效果越好。计算如下式：

2 数据采集

2.1 随钻振动信号采集

室内实验可以简化实际工程中设备和环境，实验条件可以人为控制，节约成本。

实验室用的微型实验钻机具有实际工程钻机常规功能，如加持、给进、换挡等，调整钻进参数如转速、钻速、进尺等通过一个操作面板来实现，如通过按钮加紧岩样，按钮松开岩样等。传感器为三轴加速度传感器，采样频率为51 200 Hz，在钻进过程中需注意保护传感器，避免钻孔中岩粉、冲洗液混合液溅射到传感器将其损坏。

室内实验选取7 类岩石，分别为页岩、大理岩、泥灰岩、石灰岩、粗黄砂岩、花岗岩、长石砂岩，每类岩石强度性质见表2。从表中可知每种岩石抗拉强度基本处于同一水平，且抗拉强度和钻进过程中钻头和岩石产生的振动之间的关系通常较小；每种岩石抗压强度存在差异，在钻进过程中，钻头和岩石产生的振动与岩石的抗压强度之间存在一定的关系，较高的岩石抗压强度通常意味着岩石比较坚硬，更难被钻头穿透和破碎。

表2 7 类岩石强度Table 2 Strength of seven types of rocks

为了消除样品尺寸和形状的影响，所有样品都以相同的尺寸(长宽高分别为50 mm×50 mm×100 mm)均匀制作，岩石表面均为平面。具体实验方案见表3，微钻实验振动信号采集方案如图3 所示。每次实验开始前应空钻2 min，检验实验机是否运行正常。正式钻进时，将岩石固定在实验平台，并在夹持岩样臂处安装传感器(图3a)，设置好钻头预定位置，用微型实验钻机对每类岩样施加1 组钻进参数(如200 r/min 和1 mm/min)和钻进时间，在钻进过程中持续向孔中加入钻井液冷却钻头，且能够赋予真实钻进环境，根据钻进时间和钻速可知钻进深度；在不同钻进深度阶段(0～10 mm 和10～20 mm)连续采集每个时间点的三轴加速度，每组数据采集20 s，上位机接收数字信号数据；每类岩石施加9 组钻进参数，钻取9 个钻孔(表3)。

表3 实验方案Table 3 Experimental scheme

图3 振动信号采集方案Fig.3 Vibration signal acquisition scheme

2.2 数据预处理

钻进中收集到的7 类岩石破碎产生的振动信号在时域的特征如图4 所示，显示了信号波动及幅值的变化，而在其频域特征则更加明显。在同样的钻进条件下，由于岩石岩性及其强度的不同，图4 可知各类岩石随钻三轴振动信号的时域特征都有所差别。整体上，每类岩石的Z轴振动信号加速度幅度最大，X轴和Y轴信号加速度幅度都小于Z轴，每类岩性的振动信号波动幅度也均呈现Z轴＞Y轴≈X轴的规律。在回转钻进中，压碎并切削岩石的回转能量引起X、Y轴所在平面的振动，向下钻进岩石的能量则产生Z轴振动，切削岩石相比于向下钻进岩石效率更高，那么消耗的回转能量比给进能量小，但Z轴振动加速度并不是全程都大于X轴和Y轴，只有在一些时间段内Z轴的振动幅值较高，说明钻进全过程中，给进能量并不总是大于回转能量，因此振动时域信号整体呈现此情况。

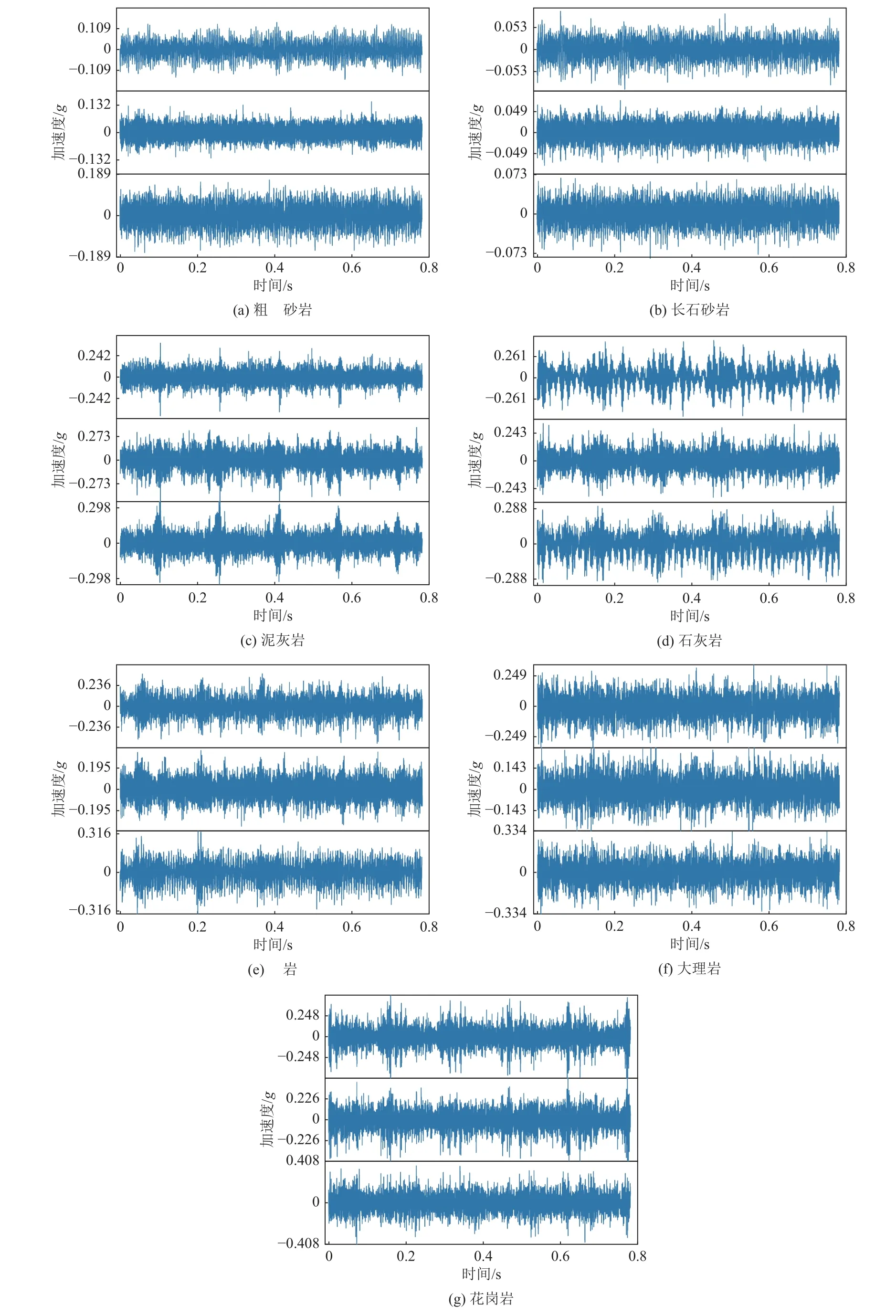
图4 原始时域信号Fig.4 Original time domain signals

原始数据往往有一些干扰信息，首先通过三点平滑滤波初步减少噪声，改善图像的质量。以振动数据识别岩性时，文献调研可知不同频段的信号有不同的作用[23]，见表4。

表4 信号不同频段的作用Table 4 Function of different frequency bands of signal

针对滤波后的时域信号设计一个截止频率为350 Hz高通滤波器，去掉信号中不必要的低频成分，以转速300 r/min、钻进深度10～20 mm、钻速3 mm/min 钻进条件为例，岩石振动频谱图如图5 所示。X、Y轴振动信号经高通滤波后显示范围为0～5 000 Hz，Z轴振动信号显示范围为0～10 000 Hz，总体上，Z轴振动信号频率范围比较宽，这与室内实验相吻合，Z轴方向为钻头钻进主要方向，振动更为剧烈，故有高频段信号。相同钻进条件下，振动信号在时域和频域上呈现出不同的变化，能够用深度学习方法提取特征，建立振动信号与岩性的联系。

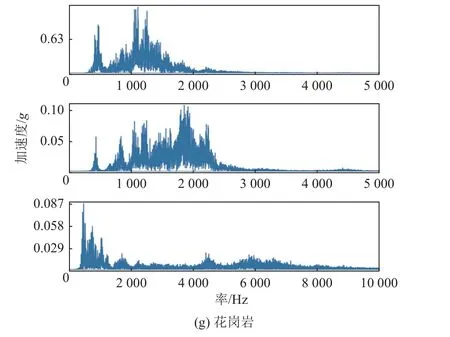
图5 滤波后振动信号Fig.5 Filtered vibration signals

为提高所有分析数据与岩性的相关性，在过高频段上振动信号并没有特征，选择0～12 000 Hz 范围的信号进行短时傅里叶变换生成时频图。调整短时傅里叶变换的关键参数，如变换选取点数、窗函数及其长度、重叠范围，选取合适的窗函数可以减少信号的频谱泄漏，并控制频谱分辨率，以确保频谱分析更准确地反映信号的时间和频率特性；窗宽的选取直接影响信号在时频域的精度，窗口越宽，频域精度高、时域精度高；窗口越窄则反之。选取样本点数、采样频率和窗口宽度相匹配，才能体现出频域的特征。经过调试，最终每张图选取65 000 数据点，汉明窗函数(窗口长度为400 数据点)，每帧的重叠范围为240 数据点，生成高精度的时频图。

振动信号经处理后，每类岩性都包含了840 张时频图，建立为数据集(共5 880 张)并划分训练集∶测试集=8∶2。对于预处理原始图像，需将所有图片进行数据增强，增加训练的数据量和噪声数据，提高模型鲁棒性，通过以下3 种方法进行数据增强，如图6 所示。第一种方法为每张原始时频图像随机垂直翻转；第二种方法为每张原始时频图像在0～30°范围内顺时针或逆时针旋转；第三种方法为每张原始时频图像的像素值在0.1～5.0 倍范围内随机变化进行亮度增强。

2.3 模型训练

构建改进VGG11 卷积神经网络结构，其网络结构参数见表5，表中输入、输出参数中三维数组如224×224×3 表示高度为224 像素、宽度为224 像素、通道数为3；一维向量如100 352×1 表示长度为100 352。开始训练之前，裁剪图片大小使其高宽分别为224×224 像素，图像由红绿蓝3 个通道组成，每一个通道为一层二维数组，计算机根据3 层同一位置的数值进行叠加来确定像素点的颜色；原始图像经过32 个大小为3×3 卷积核卷积计算形成第一层卷积层(conv1)，经卷积后特征图的尺寸会变小，通过零填充在输入数据的周围添加适当零值，以保持输出与输入尺寸相同，此操作方便网络层之间的连接和信息传递以及更好地捕捉边缘特征；接着进行池化形成第一次池化层(pool1)，通过2×2 池化窗口的目的是减小特征图的尺寸，并提取最显著的特征，通常不会进行零填充操作，特征图通道也不变；多次卷积、池化后，第一次全连接层(又称展平层，flatten)去除空间信息，将三维数组转变为一维向量，最后一层全连接层(dense3)输出7 类预测结果。设置模型超参数：学习率(learning rate)、模型训练次数(epoch)、批处理大小(batch size)，开始训练模型，测试模型拟合程度和准确率等参数，并不断调整网络结构和超参数保证获得一个准确率高、泛化能力强、鲁棒性高的模型，以准确预测岩性。

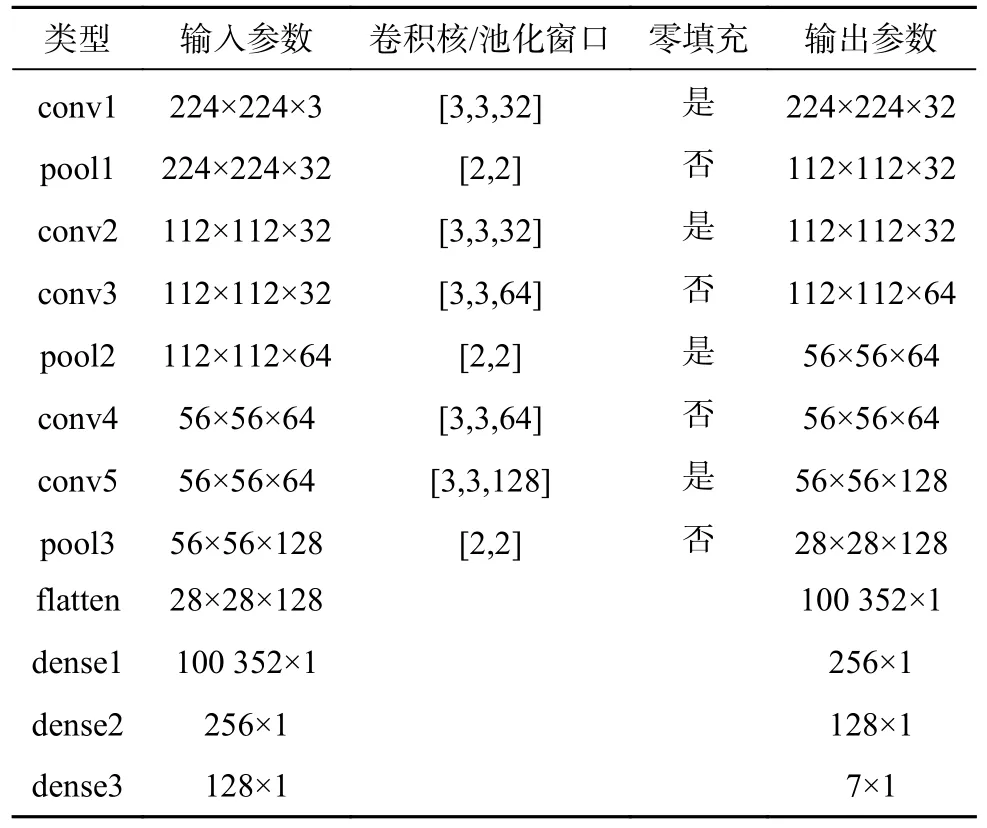
表5 VGG11 卷积神经网络结构参数Table 5 Structure parameters of VGG11 CNN

3 实验结果

通过参数调优，选取了最优超参数，见表6，学习率衰减可以使模型训练前期跳出局部最优解，后期模型稳定收敛，采用随机梯度下降衰减政策。最初学习率设为3×10-4，每次训练后衰减2×10-6学习率，100 次训练后学习率降至1×10-4，模型训练过程如图7 所示。图7a 为CNN 模型训练时的损失函数，用于表征预测标签和真实标签之间的差异值，可以判断模型的收敛情况。从图7a 中得知，模型开始训练时，训练集损失在较小的训练次数内快速下降，测试集损失同样快速下降，但围绕着训练集有一定波动；继续增加训练次数，训练集和测试集损失下降速度逐渐变慢，且测试集波动变得更小；当训练次数足够多时，两者损失值都平缓下降并逐渐趋于定值，测试集损失会稍微高于训练集，此时表明网络模型收敛。

表6 最优超参数设置Table 6 Optimal hyperparameter settings

图7 岩性预测模型训练Fig.7 Lithology prediction model training

模型每完成一次训练时，模型性能都会得到提升，随着训练次数的增加，识别精度越高，如图7b 所示。从图7b 中得知，模型训练到10 次时，训练集和测试集准确率在较小的训练次数内稳定且快速地上升，测试集准确率则有较大波动；增加训练次数到30 次，训练集和测试集准确率提高速度逐渐加快，且测试集开始拟合训练集，波动变小；当训练次数达到60 次，两者准确率缓慢提高，测试集波动进一步减小；当训练次数达到80 次及以上时，准确率不再增加，测试集会略低于训练集，模型已达到比较好的识别精度，将训练得到的CNN 模型对测试集进行测试，得到图8 的混淆矩阵，将混淆矩阵中的数据代入式(2)，计算出模型在测试集的整体岩性预测准确率为96.85%。

图8 7 类岩石预测混淆矩阵Fig.8 Confusion matrix for prediction of 7 types of rocks

为了更详细、全面地评价岩性预测模型准确率和泛化能力，基于测试集和模型精度评价标准进行评估，测试结果的混淆矩阵如图8 所示，图8 所示的混淆矩阵和模型评估指标计算式(3)-式(5)可得到各类岩石的评估指标(表7)；从图8 和表7 中可知模型对每类岩石的预测精度较高。

表7 7 类岩石评估指标Table 7 Evaluation indicators for 7 types of rocks %

对于钻进过程中岩石破碎产生的随钻振动信号，该信号特征随着岩石性质而变化，即认为一类信号代表着一类岩石。在深度学习中，将振动信号的时频能量变化预处理为图像并使其可视化，构建的网络结构合理的CNN 模型具有强大的特征提取能力，对于岩石岩性数据集的预测效果好。

4 讨论

4.1 数据集对预测准确率的影响

为得到一个表现优秀的CNN 模型，需不断调试网络，通过不同的影响因素优化模型，现已知可调整数据集数量、训练次数等。

通过逐渐增加数据增强方法得到更大的数据集，增强前数据集数量有5 880 张图像，增强后数据集分别有8 820、11 760、14 700。划分数据集比例后，训练集数量分别为4 704、7 056、9 408、11 760，测试集数量为1 176、1 764、2 352、2 940。各数据集训练后的识别准确率如图9 所示，数据集数量的增加对模型识别精度有一定的提高，且当样本数量足够多时，该模型准确率达到最优，不再变化。

图9 数据集数量对准确率影响Fig.9 Impact of dataset size on accuracy

4.2 转速对信号的影响

7 类岩石的三轴振动信号在不同转速条件下的变化情况如图10 所示。总体上，X、Y轴信号主要响应在0～5 000 Hz，分布范围Y轴稍大于X轴，Z轴则分布于更广的范围(0～10 000 Hz)。在保持钻速3 mm/min的条件下，随着转速的增加，X、Y轴信号的分布范围变广、幅值增大，并且能量集中频段逐渐转向更高的频率，由于钻头回转方向在XY轴平面上，增加转速会使得钻头在单位时间切削更多的岩石，与岩石的响应表现为更为剧烈的环向振动，碎岩能量更高。转速对Z轴信号的影响不明显，总体表现为信号幅值的小幅度增长，可能是由于环向振动的加剧使钻头能够更高效向下钻进岩石；随着钻速的增大，Z轴信号的集中频段向高频率移动，幅值增加相对更大，这是由于碎岩速率增大，钻头与岩石的响应表现为轴向振动加剧。

图10 不同转速下三轴振动信号Fig.10 Triaxial vibration signals at different rotary speeds

图10 中X、Y轴振动信号频率范围显示为0～5 000 Hz，在更高频段并没有加速度，而Z轴显示为0～10 000 Hz，所以Z轴信号在5 000～10 000 Hz 的振动加速度比X、Y轴振动加速度幅值大，但这个范围的加速度幅值在总体上是比较小的。出现此情况初步分析为钻头钻进岩石时，首先钻头切削岩石，在XY轴平面产生了X轴和Y轴振动，由于切削过程需要较大的力，产生的振动加速度幅值较大，然而，由于岩石切削过程相对较慢，频率响应可能不会很高，通常在0～5 000 Hz，此时切削岩石使得岩石有一定破碎，所以向下钻进破坏岩石不需要更大的力，产生的Z轴振动加速度幅值基本上要比X轴和Y轴振动小一点，需要更多的振动以高效碎岩，振动频率响应可能会相对较高，所以Z轴方向产生了更高频率范围的响应，范围在0～10 000 Hz。

对振动特性的分析主要集中在转速和钻速，转速和钻速对随钻三轴振动信号的影响为岩性智能预测模型的泛化性提供了一定基础，因此成功地应用深度学习技术建立了岩性预测模型，但存在一定局限性，如未能记录和分析钻压对振动信号的影响，这可能导致岩性预测模型在某些情况下的准确性和可靠性受到一定限制。可以通过增加钻进条件和记录更多钻进参数获取振动信号的多样性变化，如钻头直径、钻头类型、钻压等。在实际工程中，钻进参数、环境会不断变化，高泛化性的模型能适应这种变化，准确预测岩石性质。

4.3 振动信号时频域特征分析

从每类岩性的时域信号特征来看，粗黄砂岩和长石砂岩的振动加速度最小，波动相对稳定，这与它们的力学物理性质(如抗压强度等)相关，这两类属于相对较软的岩石，破碎时产生的振动小；泥灰岩和石灰岩振动加速度稍高于前者，其抗压强度更高，性质较硬，波动幅值增加；页岩和大理岩力学性质进一步增大，三轴振动加速度也增加；花岗岩在7 类岩石中具有最大的三轴振动加速度，稍高于页岩和大理岩，其抗压强度却不是最大，由此可知，有多种因素影响随钻振动幅度及波动，如岩石微观结构、岩石成分、岩石破坏特征等方面，可观察这些特征以更加全面地分析时域振动信号的规律。

在频域上，岩石的性质(如岩性，抗剪强度、单轴抗压强度等物理力学参数)不同，岩石与钻头、钻柱的响应有各自的特点。从滤波处理后的频谱图可得知不同岩性的频谱的变化情况及其集中频段各不相同。

从总体上看，三轴信号主要分布在中低频范围，Z轴振动信号代表钻头向下钻进岩石，能分布在更高的频段(6 000～10 000 Hz)，X、Y轴信号表征钻头切削、磨蚀岩石以向下高效碎岩，信号高频段幅值几乎为0，即分布范围Z＞Y＞X。

在能量分布上，信号都集中于低频段，能量集中有所差别，Z轴信号高能量集中于很小的范围(约1 000 Hz)，集中范围Y＞X＞Z。粗黄砂岩和长石砂岩的力学参数小，能量幅值最小；泥灰岩、页岩、花岗岩性质较硬，能量幅值增大；大理岩和石灰岩的能量幅值最大；花岗岩相较于石灰岩有更高的力学参数，能量反而小，即振动信号在频率上的分布与岩石的其他性质(如岩石成分、粒度、微观结构等)有关。

在钻进岩石过程中，向下碎岩能量主要集中在Z轴振动上，且岩石有自身的固有频率，钻进时产生的振动大部分能量分布在该频率附近(共振：受到外界激励时产生的响应表现为大幅度、高频次的振动)，以达到高破岩效率。

7 类岩石时域信号幅值大体上随着抗压强度增加而增加，而频域信号幅值变化规律却不同。泥灰岩和石灰岩、花岗岩和页岩强度参数基本一致，在考虑实验误差的前提下，并不能单从抗压强度完全分析和总结信号时域和频域特征，还需考虑到每种岩石的固有频率规律、钻进工具、破岩机理(冲击(Z)、切削(X、Y)、磨蚀等)及岩石破坏特征等多个因素的综合影响，并进行详细的实验和观测研究。

5 结论

a.通过采集钻进过程的三轴振动数据，将数据进行短时傅里叶变换生成时频特征图像并构建为数据库，建立了基于VGG11 卷积神经网络的岩性智能预测模型，预测准确率达到96.85%，即利用岩石钻孔产生的随钻振动信号可以较准确地预测岩性。

b.研究数据基于设计室内实验，采集的数据干扰数据较少，重点分析了每类岩石的三轴振动信号时域、频域特征以及不同钻进条件下振动信号的变化；同时高质量的数据集为岩性智能预测模型的高精度提供了基础，而在实际工程中获取的数据，需要注意对信号中无用信息的滤除。

c.提出的岩性智能预测方法可以实时预测钻进岩体情况并快速调整随钻参数，符合快速、安全钻进的需求；并且预测速度快、准确率高，能降低岩性识别对工程经验、专业知识的依赖，帮助解决传统岩性识别方法存在费时费力、不能实时识别等问题。

d.本文提出的岩性预测模型暂未应用于工程现场，后续将依托工程现场采集多个钻孔的振动数据，对该区域的其他钻孔进行预测，并通过引入更多相关参数(钻压、钻具设计等)和分析振动信号与参数的关系，进一步改进岩性预测模型，提高其在实际应用中的准确性和可靠性；同时将继续开展岩石力学性质(如抗压强度、抗剪强度)反演研究，将随钻参数(钻压、转速、扭矩等)和钻进响应(声音、振动)作为多源信息融合数据，对岩性和力学参数进行智能预测，显著提升预测模型的泛化性和鲁棒性，以适应工程实际。