弱模型依赖的运载火箭液体晃动自适应控制方法公开
2023-09-27史丽楠王光辉李光杰
纪 刚,史丽楠,王光辉,王 飞,李光杰
(北京航天自动控制研究所,北京,100854)
0 引言
液体晃动不稳定导致姿态控制困难的难题,自20世纪60年代初,就得到航空航天设计师的关注。1969年,Apollo-11月球探测器首次于月球表面着陆的最后几秒中,残余液体燃料的晃动引起本体姿态抖动,进而导致落点精确度受到影响。1998年,NASA发射的NEAR(Near Earth Asteroid Rendezvous)探测器本体运动与推进剂晃动之间产生了耦合,整个任务过程被拖延了13个月。2007年3月,Falcon-1二级运载火箭第二级在进入太空后失去控制而未完成预定任务,液体推进剂的晃动极有可能是此事故发生的主要诱因[1]。
为了引入液体晃动对系统动力学与控制的影响,工程上通常在液体处于小幅晃动时,将液体的晃动等效为一个弹簧振子,以便与刚体、弹性模态共同构建火箭箭体动力学模型。液体晃动阻尼通过理论计算得到的解析解或近似解需要进行试验确认[2]。实际飞行的结果分析显示,晃动的频率理论值也存在一定的偏差。液体运载火箭推进剂晃动运动,由火箭箭体的姿态运动的牵连惯性力所激励[3]。姿态控制系统应对晃动不稳定问题,常采用被动控制与主动控制两种策略。被动控制采用增加防晃结构的方法,但这会损失火箭的运载能力,也会使结构建造变得复杂,难以适应任务的多变性。主动控制则通过提升晃动频段的相位裕度或者限制晃动谐振幅值来实现[4]。液体晃动采用幅值稳定的基本条件,要求刚体的截止频率与晃动频率拉开足够的安全距离,对晃动信息进行滤波时不能以大幅牺牲刚体相位稳定裕度为代价。采用相位稳定则需对晃动运动进行主动干预,确保控制的过程始终处于负反馈的状态,然而当晃动模态处于极零结构分布时,采用相位稳定则异常困难甚至无解。文献[4]给出了加速度计安装在火箭质心处的测量方程:
通过分析,对加速度计反馈参与控制后晃动的极点变化给出了定性结论。文献[4]同时指出,采用加速度反馈,可以使晃动的极点发生变化,当晃动极点向高频移动,则有实现极零结构向零极结构转换的可能,但如果晃动模态本身处于稳定的零极结构,这种反馈方式则可能起到相反的作用。
文献[4]在加速度反馈方法分析的过程中,简化并忽略了姿态角加速度的影响,然而实际中当晃动所造成的干扰力矩已经严重到火箭箭体姿态运动时,该项的影响不能忽略,式(1)需改写成式(2)所示的形式,其中Δ可等价于。
中国在低重力充液航天器晃动抑制方面有较多的研究。朱志浩等[5]提出了一种有限时间控制律,利用输入成型器对航天器姿态大角度机动的期望信号进行调制,有效抑制了残余振动和液体晃动。孙平等[6]综合动态逆控制,设计了有晃动运动时的飞行器姿态控制律,由状态反馈实现姿态跟踪和晃动抑制。顾黄兴等[7]针对一类带液体燃料晃动的航天器,设计了一种滑模控制器,可以较好地使系统的部分状态量达到平衡点。宋晓娟等[8]针对充液航天器大角度姿态机动问题,设计了基于自适应动态输出反馈控制器及多模态前馈输入成型技术的复合控制器,实现了姿态与晃动的控制。吴文军等[9]在建立低重力环境下航天器刚-液-柔-控耦合非线性动力学模型基础上,研究了该类航天器在不同工况下的刚-液-柔耦合动力学性能。邓明乐等[10]则推广了运动脉动球模型,并且提出了对应的自适应滑模控制方法。
液体运载火箭不同于低重力环境下的航天器,飞行中存在轴向大过载和大结构干扰,火箭箭体参数随时间变化大。与运载火箭的刚体和弹性模态相比,液体燃料具有的流动性特征导致其小偏差线性模型中的阻尼项是时变参数,尤其当晃动模态处于严重的极零不稳定分布状态时,控制参数对模型的依赖程度过高,而晃动模态本身是需要通过液体晃动试验校核理论计算的,实际工程中,这一环节在积累了大量的经验后经过论证是可以被简化的。常规的PD 控制方式在控制裕度足够大时,上述的试验校核可以被容忍,但在晃动处于极零不稳定状态时,难以在晃动稳定和刚体、弹性模态稳定之间得到最优解,甚至存在难以调和的矛盾。因此必须降低控制方法对模型的依赖程度,以提高对模型不确定性的适应性。
自适应控制在运载火箭控制领域有较为丰富的研究成果,其中比较有代表性的为张亮[11]针对重型运载中弹晃耦合问题,设计出自适应滤波器实现在线滤除弹性振动信号,有效地减弱了弹性对晃动的影响。韦常柱[12]针对运载火箭主动段强干扰、大不确定性、弹性振动变化及高结构载荷综合影响的问题,研究自适应增广控制系统综合设计方法,具有理论研究意义和工程应用价值。这些成果推动了自适应控制方法在运载火箭的应用,但在火箭不稳定晃动模态的研究方法方面研究较少。此外,邵会兵等[13]针对气动参数大范围变化的问题,开展了基于深度学习(Deep Learing,DL)的自适应姿态控制、基于深度确定性策略梯度算法(Deep Deterministic Policy Gradient,DDPG)的通用姿态控制、弱模型依赖的多维复合控制等技术研究,对于提高系统的鲁棒性和通用性做出了分析研究。
针对运载火箭的不稳定液体晃动难以设计的问题,本文将晃动方程转化为与刚体和弹性动力学相关联的力矩干扰模型的控制补偿问题,利用扩展状态观测器对晃动力矩干扰进行估计提取,实现在线实时卸载补偿,并用典型的仿真证明了方法的有效性。
1 动力学模型
1.1 动力学方程简化
火箭液体推进剂参与晃动运动的质量主要考虑其一次谐波的影响,由于运载火箭贮箱液体晃动的频率相对质心运动频率较高,不考虑质心运动和气动等外干扰,采用如式(3)所示的姿态运动方程作为研究对象。
式中 Δ为火箭箭体系俯仰角偏差;δφ为俯仰通道控制摆角;b3为控制力矩系数;b4p为液体晃动质量所产生的力矩;Δyp为第p阶晃动的广义位移;Δ为第p阶晃动的加速度;XT为火箭质心距离火箭理论尖点的距离;Xla为晃动质心距离火箭理论尖点的距离;k3为发动机摆角对液体晃动的激励系数;k41为晃动质量自身运动的激励系数。
从式(3)中可以看出,晃动动力学方程与刚体动力学方程之间的联系变量为晃动广义位移Δy、晃动加速度项Δ、发动机摆角Δδφ及火箭箭体角加速度Δ。当系统稳定裕度不足的情况下,液体晃动加剧,联系变量Δ和Δy使得火箭箭体角加速度逐渐变大,进而通过Δδφ和Δ对不稳定的晃动造成二次激励,最终导致液体晃动和火箭箭体姿态出现不稳定发散的趋势。
图1为自由液面晃动质量与火箭箭体相互作用的示意。飞行中液体真实的晃动阻尼快速时变,是流动体相比刚体模态和弹性模态的最大差异,液面运动至高位,其液体晃动作用力达到最大,同时晃动阻尼也达到了最大,而液面恢复到最低位时液体晃幅最小,对火箭箭体的作用力最小,但阻尼却接近零。图1中O1为箭体质心,也是箭体坐标系坐原点,x1轴指向箭体前端为正,z1轴指向右为正,y1遵守右手定则,Phd为晃动质量的作用力及其作用方向。

图1 自由液面与火箭箭体相互作用示意Fig.1 Diagram of interaction between free liquid surface and rocket body
常规液体晃动的稳定性设计,主要通过改变液体晃动特性参数来实现。改变液体晃动频率使其与刚体运动频率、控制频率不耦合,减小液体晃动质量弱化晃动力和力矩,提高晃动阻尼增大稳定裕度,或者改变晃动质量的相对位置消除晃动模态的结构不稳定。当主任务指标确定,在运载能力、设计和生产周期等多因素约束下,工程优化晃动特性的方法是有限的。
1.2 测量方程的建立
惯性器件提供了火箭飞行过程中火箭箭体的运动状态参数,实现了对姿态角和的视加速度测量。
不考虑弹性交联项,陀螺测量方程如式(4)所示:
式中ωy1(xgz)、ωz1(xgz)分别为y陀螺和z陀螺测量到的角速度;ωy1、ωz1分别为刚体部分绕火箭箭体系o1y1轴和o1z1轴的角速度;Ryi(xgz)、Rzi(xgz)分别为惯组安装处弹性振型斜率;、分别为弹性广义位移的变化率。式(4)中弹性频率与液体晃动频率的相差较大,在弹性信息分析中可以忽略。如果将等式左边的角速度部分展开,其中包含晃动力矩在火箭箭体上引起的角加速度积分项。
火箭弹性频率与质心运动和绕心运动频率相比一般较高,因此y1和z1方向加速度计的测量方程可采用如式(5)所示的描述形式:
式中,分别为火箭质心处的法向和横向的视加速度;lax为y、z加表安装位置与实际质心距离,对于加速度测量信息影响最大的主要是lax项;laz为y加表安装位置与O1x1轴的距离;lay为z加表安装位置与O1x1轴的距离,由于laz和lay两项数值相比lax很小,可不作考虑。视加速度的来源还包含来自弹道的激励,此处可不考虑。
一般情况下,液体火箭的晃动频率相比弹性频率更接近刚体频率,因此极易对系统的稳定性造成危害。图2给出了典型火箭姿控系统相关的模态频率分布特征。

图2 运载火箭特征频率分布Fig.2 Characteristic frequency distribution of carrier rocket
2 弱模型依赖的晃动自适应控制
2.1 姿控系统稳定性设计
姿控系统利用惯组实现对火箭箭体角运动信息φ(t)的测量,与程序指令r(t)求取偏差e(t),由PD 控制器产生控制指令δc(t),通过伺服机构输出真实摆角δφ(t),进而实现图3所示全回路的闭环稳定控制。

图3 姿控系统控制框图Fig.3 Control block diagram of attitude control system
当火箭箭体晃动模态出现不稳定极零分布时,火箭箭体开环传递函数中会出现图4所示的幅、相频特征。此类对象的控制参数设计具有典型的多约束特征,提高晃动频段的相位超前,达到一定安全的相位裕度,则会导致上限状态缸体高频幅值裕度的大幅度损失,同时对高频弹性的幅值裕度以及高频抗干扰能力也会造成损失。

图4 典型火箭箭体开环传递特性Fig.4 Open-loop transmission characteristics of typical rocket body
造成以上设计难点的主要因素在于刚体截频与液体晃动频段没有拉开足够的距离,使得幅值衰减措施不可以贸然实施,而提高相位的措施也会导致系统抗高频干扰的性能大幅度下降。
通过前文分析,晃动对于火箭箭体的耦合效应主要是通过火箭箭体受到的晃动干扰力矩物理环节闭合形成,因此构造如图5所示的晃动与姿态耦合描述框图。图5中,将晃动特征建立成刚体和弹性体姿态动力学的干扰力矩描述方程,并作为一项待补偿项进行研究。

图5 姿控系统晃动模态干扰原理Fig.5 Slosh mode interference for attitude control system
从式(3)中的液体晃动运动方程可以看出,理论上只要对等式右端的(XT-Xla)Δ进行合理的处理,是可以减小火箭箭体角加速度与晃动干扰力矩的耦合效应的。
2.2 晃动干扰力矩信息辨识提取
角加速度信息能够直接表征角运动的高阶性,当捷联惯组作为火箭主要惯性测量设备时,陀螺所测得的火箭箭体系角增量是角加速度信息辨识的唯一信息源,考虑工程实际,捷联惯组只能安装在火箭靠近头部的仪器舱。
利用非线性扩张状态观测器(Extended State Obsever,ESO)自抗扰[14],据此将式(3)写成如式(6)所示的二阶对象形式。
式中x1=Δφz1,x2=Δ,b=-b3,u=δφ,f(x1,x2,w(t),t)为包含液体晃动引起的干扰力矩在内w(t)的总的干扰。
将总干扰作用下的f(x1,x2,w(t),t)作为一个新的观测量,则原系统扩张为一个新状态,选择合适的参数即可达到较好的观测效果。为提升液体晃动对绕心运动干扰力矩辨识的准确性,运载火箭的弹性频率和晃动频率需存在足够的安全距离,工程实践中可按照5倍以上设置。
晃动运动对火箭箭体产生的干扰力矩影响,在一段时间内集中在相对固定的频段,频率随过载的变化而变化。角加速度辨识的结果用于晃动不稳定运动的抑制,不应对刚体跟踪程序指令有不良影响,同时也需要对测量信息中包含的高阶弹性信息进行滤波,需根据液体晃动频率进行设计。
对低频结构扰动力矩和高频弹性扰动力矩进行滤波,保留晃动频段的扰动信息可对状态观测器得到的角加速度进行带通滤波。选择如式(7)所示二阶带通滤波器即可实现对晃动频段信息的提取。
式中ξ0为二阶滤波器阻尼系数;K为滤波器通道增益;ω0为带通中心频率即晃动频率。频率的选择尽可能避免对飞行中对其他模态和制导指令产生影响,重点覆盖晃动不稳定现象严重的时间段。
2.3 液体晃动自适应补偿卸载
典型的晃动极零不稳定,会造成的晃动频段相位损失90°以上,通过微分环节提高相位裕度的代价是较大的。
液体运载火箭动力学模型具有较高的应用成熟度,基于标准弹道设计的火箭箭体刚体参数偏差范围是比较准确的。飞行中,火箭箭体参数会因弹道不同、燃料消耗偏差等有所差异。随着液体质量的消耗,晃动频率逐渐变大,晃动质心位置逐渐变化,与晃动质量相关系数等都会随之发生变化。理论计算和实践经验认为液体晃动的频率是与火箭箭体的过载强相关的。将晃动部分视为相关但可独立于刚-弹模型之外的干扰力矩,弱化晃动模型作为常规设计的一环,仅将其作为与刚体运动关联的干扰力矩模型,并构造如图6所示的液体晃动自适应补偿控制原理。

图6 晃动模态自适应补偿控制原理Fig.6 Slosh mode adaptive compensation control
图6 中,常规的PD 控制器主要保证刚体和弹性模态的稳定裕度。在仅考虑刚体和弹性稳定的条件下,系统的Bode 图如图7 所示,显然晃动是没有晃动稳定裕度的,而刚体和弹性的稳定裕度是足够的。
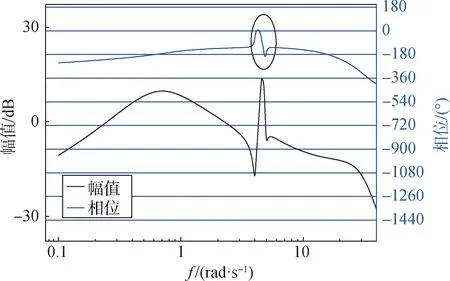
图7 包含晃动模态的火箭箭体Bode图Fig.7 Bode diagram of rocket body containing shaking modes
式(6)中,火箭箭体角加速度反映了全箭的干扰力矩,通过式(7)滤波处理之后,干扰力矩信息以晃动频段为主,其主要的特征表现为不稳定晃动模态的频率以及幅值,而涉及晃动运动的其他信息则不作为重点。
建立式(8)所示补偿公式,以俯仰通道为例进行描述,偏航通道的补偿公式与之类似。
其中,a2为干扰力矩补偿的前向增益,是与火箭箭体晃动特性、飞行时间t、晃动模态时间thd、晃动质量mp、惯组距离火箭质心距离lax、轴向过载Nx、晃动频率ωhd以及相位差Δθhd等相关的函数,表达式如式(9)所示,Δ为经过滤波处理后的晃动频段俯仰通道角加速度信息。
前向增益的设计可据需求设计相应的非线性限幅函数,需要明确,对于晃动模态非极零结构或者可以通过设计达到充足稳定裕度时,无须特别考虑自适应卸载补偿的方法。
3 仿真验证
以某运载火箭二级飞行段模型为研究对象,仿真设定俯仰、偏航和滚动通道姿态角偏差初值为0°,姿态角速度初值为0(°)/s,晃动初始位移为0 m,发动机摆角初值为0°。
将状态观测器估计并提取得到的晃动频段干扰力矩补偿信息引入控制回路,结合自适应调节前向补偿卸载增益,对不稳定的液体晃动质量所产生的干扰力矩进行衰减。晃动干扰力矩和补偿指令如图8 所示,可见系统对于衰减晃动的指令需求是很小的。
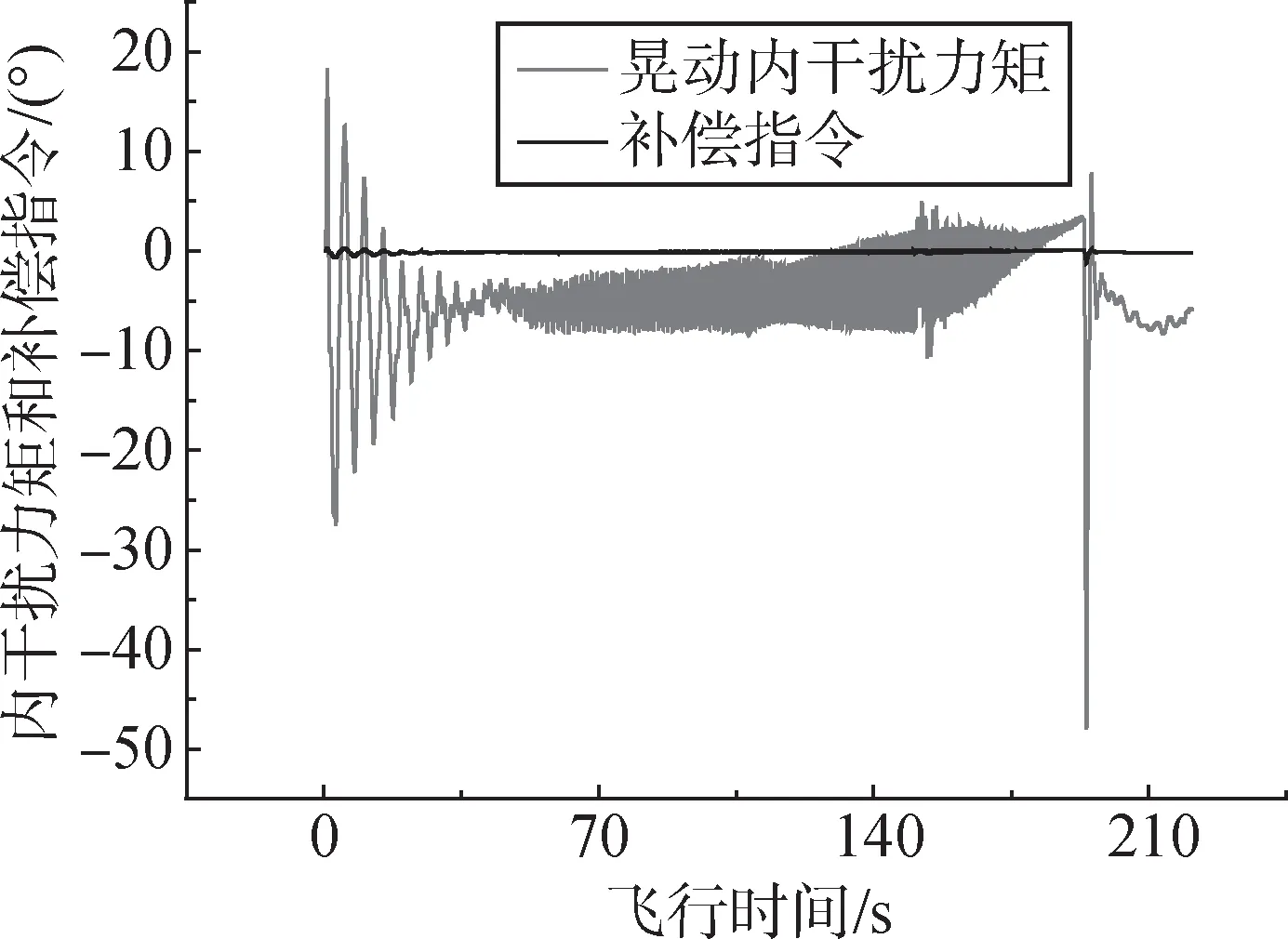
图8 法向晃动干扰力矩和补偿力矩Fig.8 Normal sloshing internal interference torque and compensating torque instruction
下面给出俯仰通道的典型仿真结果。补偿指令闭合到系统后,图9 中火箭箭体姿态实现了快速收敛,姿态角偏差峰峰值最大的衰减率接近38倍。图10中,液体晃动幅值有效抑制,补偿前的液位达到了上限幅值,补偿后晃动幅值较小且无发散趋势。图11中发动机摆角等参数均进入了合理的范围之内。
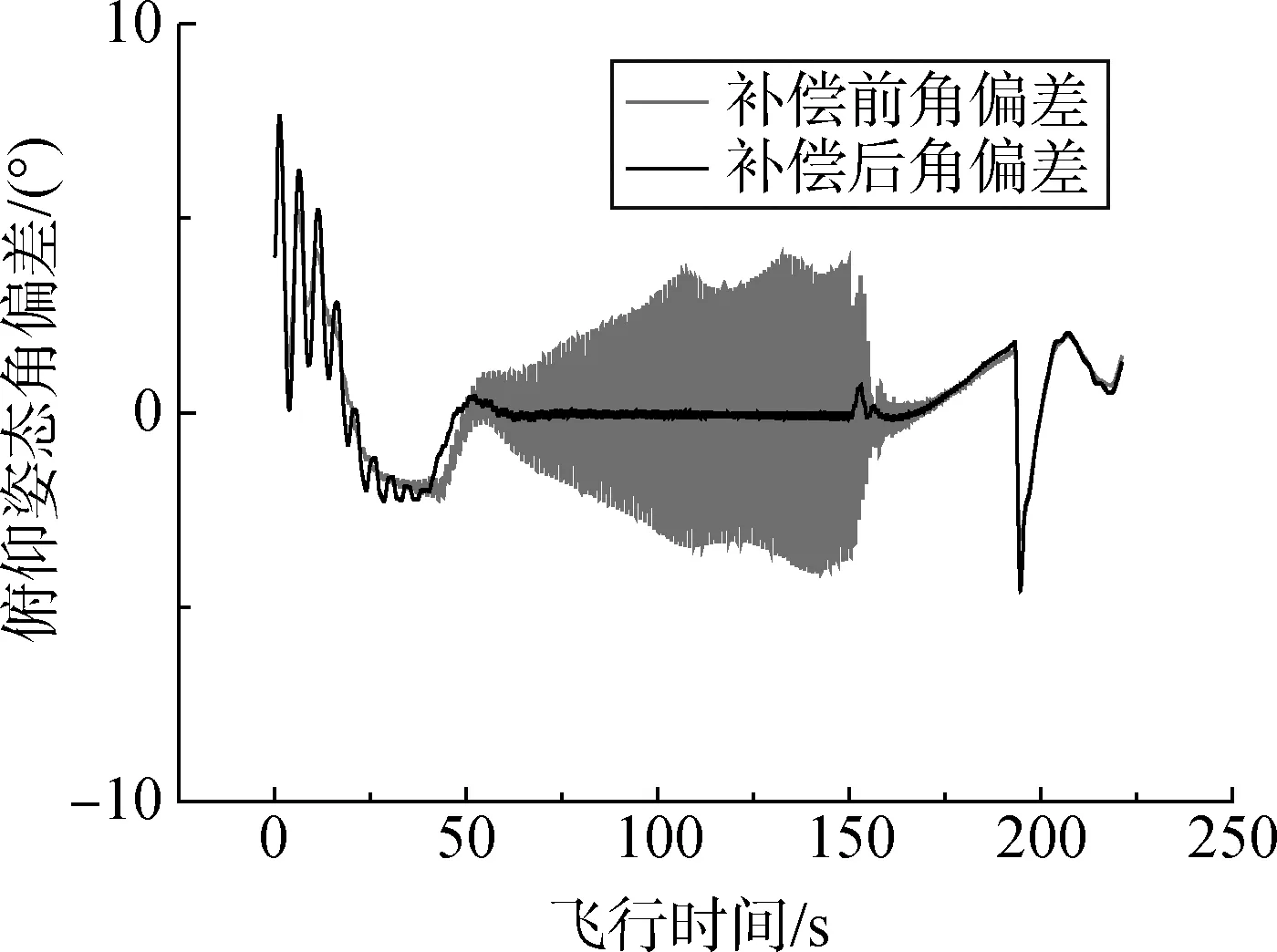
图9 俯仰通道姿态角偏差Fig.9 Pitch channel attitude angle deviation

图10 法向晃动位移Fig.10 Normal shaking displacement

图11 俯仰通道发动机摆角Fig.11 Pitch channel engine swing angle
从典型状态下的仿真效果来看,针对不稳定晃动力矩干扰的补偿是有效的,不仅保证了自由液面的晃动处于相对稳定的状态,姿态角偏差控制在很小的范围之内,发动机摆角也在相对合理的水平。
4 结束语
本文提出将晃动运动方程的描述视为一种具有阻尼特征且时变的力矩干扰,利用扩展状态观测器估计系统的总干扰力矩并提取晃动频段信息,设计了基于晃动频段信息辨识的自适应实时卸载补偿方法,典型的仿真证明了该方法的有效性。弱模型依赖的控制方式减少了对建模精确度的要求,为智能化控制解决晃动不稳定的疑难问题提供了新的思路,但同时对于系统稳定性的证明需要深入分析,对晃动频段干扰力矩的提取以及本文所述的方法在工程中使用的禁忌需要进行研究。
