基于遗传算法的常规复合式高速直升机飞行性能参数优化

曾怡兰，韩东，刘壮壮

1.南京航空航天大学 直升机动力学全国重点实验室，江苏 南京 210016

2.中国航天空气动力技术研究院，北京 100074

进入21世纪以来,追求高速成为国内外直升机技术领域的重要发展方向。高速直升机能够快速高效地完成作战任务,拓宽直升机应用领域,目前在国外直升机行业内研制较为成功的高速直升机构型主要是倾转旋翼机、共轴刚性旋翼直升机和复合式直升机[1-3]。

常规旋翼构型复合式直升机在传统直升机基础上去掉尾桨部件,增加机翼、螺旋桨等升推力装置,可改善旋翼前行桨叶的桨尖激波和后行桨叶的气流分离导致的不利影响,提高直升机的最大飞行速度。由于采用了多升力面、多推进面、多操纵面技术,常规旋翼构型复合式直升机的总体布局、总体参数选择、质量重心设计、气动布局、气动效率对全机的飞行性能、飞行特性、飞行品质都具有决定性的影响[3]。为进一步提升其飞行性能,国内外围绕总体布局和性能优化等方面开展深入研究。H.Yeo[4]分析了高前进比下H-34、UH-1D 和UH-60A 的旋翼性能和AH-56A 复合式直升机的全机性能,研究表明,升力复合布局增大了全机升阻比的最大值,推力复合布局改善高速时的升阻比,完整的复合布局结合了升力和推力复合的特性,全机升阻比最大值和高速时飞行性能均有改善。K.Ferguson 等[5]评估了共轴复合式直升机和常规复合式直升机的性能,并与传统直升机进行比较。结果表明,常规复合式比传统直升机消耗更多功率,为降低高速时的阻力,复合式直升机需要优化机身设计。M.W.Floros 等[6]采用CAMRAD Ⅱ软件计算了降速旋翼的复合式直升机性能,高速下自转旋翼的最优总距发生在旋翼产生少量正拉力时,减慢旋翼转速可降低复合式直升机的需用功率。杨克龙等[7]以加装机翼和螺旋桨的UH-60A直升机为例,探讨了机翼和螺旋桨参数、升推力分配对全机性能的影响机理。性能优化方面,O.Rand等[8]引入“阻力/功率图”和基于非线性自由尾迹分析方法的优化策略,分析表明复合式直升机的最优配置依赖于旋翼、推进器和机翼的效率。S.Hersey等[9]提出一种将基本优化问题转化为一系列近似优化问题求解的多目标优化方法,在带有升推力装置的共轴复合式直升机模型上进行了应用。此优化方法鲁棒性好,能够处理多个局部最优问题。王坤等[10]采用基于6σ 设计的改进多目标遗传算法对共轴复合式直升机的总体参数进行优化,优化后的复合式直升机飞行性能得到较大改善。C.Lienard等[11]对RACER验证机的垂尾外形采用基于多保真算法的外形修正及优化策略,修正后的垂尾能有效地降低气流分离,满足设计要求。

本文在已有直升机飞行性能分析模型基础上,引入Young曲线拟合和动量叶素理论对悬停和低速下产生负拉力的螺旋桨建立气动模型,以样机X3直升机总功率为优化目标,选用旋翼、螺旋桨等部件参数为优化变量,构建基于遗传算法的性能优化模型,分析不同飞行状态优化后直升机性能,并研究基于遗传算法的参数优化对常规复合式直升机的各类功率和操纵量等特性的影响。

1 复合式直升机建模及性能计算

1.1 复合式直升机飞行性能分析模型

本文建立的常规复合式直升机模型由旋翼、螺旋桨、机翼、机体和平尾、垂尾6 部分构成。悬停和低速时,左右螺旋桨的拉力相等但方向相反,以平衡旋翼反扭矩；飞行速度超过210km/h后,两侧螺旋桨均提供正前进力,利用垂尾侧向力去抵消反扭矩。旋翼模型以叶素理论为基础,根据Pitt-Peters 动态入流理论[12]计算诱导速度,由桨叶惯性力、离心力和气动力对挥舞铰力矩平衡求解桨叶挥舞角,最后进行数值积分得到旋翼桨毂力和力矩。机翼、平尾和垂尾基于升力线理论[13]建立气动模型。由参考文献[14]确定机身阻力,体现前飞时机体模型对废阻功率和配平的影响。产生正向拉力的螺旋桨建模方法[15],采用动量叶素理论[16-18]得到螺旋桨力和力矩。

当螺旋桨产生负向拉力时,随着前飞速度的增大,螺旋桨会依次经历涡环、湍流和风车状态。本文采用Young 曲线拟合[19]结合动量叶素理论方法建立产生负拉力的螺旋桨模型。图1为由Young曲线拟合给出负拉力螺旋桨的轴向诱导速度。

假定V0为来流速度,vi为实际飞行状态下螺旋桨桨盘处的诱导速度,vh为悬停状态下的桨盘处诱导速度。Young曲线拟合得到的涡环和湍流状态的诱导速度分别为

式中,螺旋桨的理想自转条件为V0= 1.75vh。

图1 Young曲线拟合求解诱导速度Fig.1 Young curve fitting to solve for induced velocity

若以较大速度前飞,螺旋桨处于气流稳定的风车状态,螺旋桨模型基于动量叶素理论建立。

距离螺旋桨桨盘中心rp、宽度为drp的环带轴向速度va和周向诱导速度vb分别为

式中,V0为来流速度；dTp和dQp为螺旋桨环带的拉力和扭矩。

根据前飞速度确定螺旋桨状态,将初始后由叶素理论得到的环带拉力和扭矩,代入式（1）～式（4）计算新的轴向和周向诱导速度。通过不断修正轴向和周向诱导速度,直至迭代收敛确定螺旋桨各剖面的力和力矩,进行数值积分后得到螺旋桨总拉力和总扭矩。

复合式直升机的配平方程求解见参考文献[20]。由经验公式给定初始操纵量和姿态角后,利用牛顿迭代法求解近似根直至收敛,得到配平后各部件气动力和力矩。与常规直升机总功率计算不同,复合式直升机总功率由旋翼功率和螺旋桨功率两部分组成。

1.2 气动部件模型验证

采用UH-60A直升机的飞行试验数据[21]验证旋翼模型的正确性,其旋翼和尾桨的参数见参考文献[22]、[23]。图2给出了在直升机质量系数Cw分别为0.0065、0.0074时,旋翼功率系数的模型预测值与飞行数据的对比,预测值与试验值数据吻合较好。

图3给出了不同前进比时螺旋桨拉力系数和功率系数的模型预测值与飞行数据[24]的对比,验证的螺旋桨相关参数见参考文献[24]。将螺旋桨前进比定义为

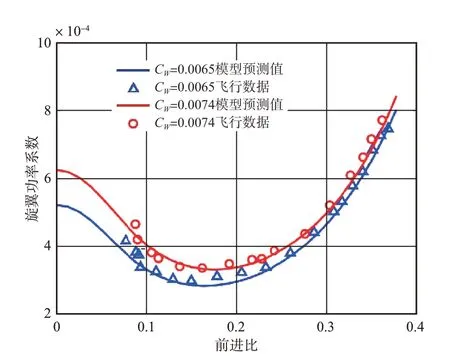
图2 旋翼功率系数的预测值与试验值对比Fig.2 Comparison of rotor power coefficient between prediction and test data

螺旋桨的拉力系数和功率系数分别为

式中,V0为来流速度；nP为螺旋桨转速,DP为螺旋桨直径。从图3可以看出,预测值与试验值数据吻合较好。

图3 螺旋桨拉力系数和功率系数的预测值与试验值对比Fig.3 Comparison of propeller thrust and power coefficient between prediction and test data

2 性能优化模型

遗传算法是模仿自然界生物进化机制而发展起来的随机全局搜索和优化方法[25]。通过对算法中的种群个体进行编码,确定好适应度函数后再进行选择[26]、交叉[27-28]和变异[29]操作,不断进化得到满足条件的最优个体或最优适应度。

本文以X3 复合式直升机的总功率为优化目标即适应度函数,选用旋翼、螺旋桨、机翼和平尾部件的特征参数为优化变量,基于遗传算法建立复合式直升机的性能优化模型。样机的原始参数见参考文献[15],优化变量中旋翼和螺旋桨的半径、机翼和平尾的展长、面积在原值20%范围内,而旋翼和螺旋桨的桨尖速度是由桨尖速度不超过声速和平衡最大最小值与基准值的差值而定的,变量取值范围见表1。性能优化流程如图4所示,最终得到直升机的最优功率和优化后的变量值。

表1 优化变量取值范围Table 1 Ranges of optimized variable values

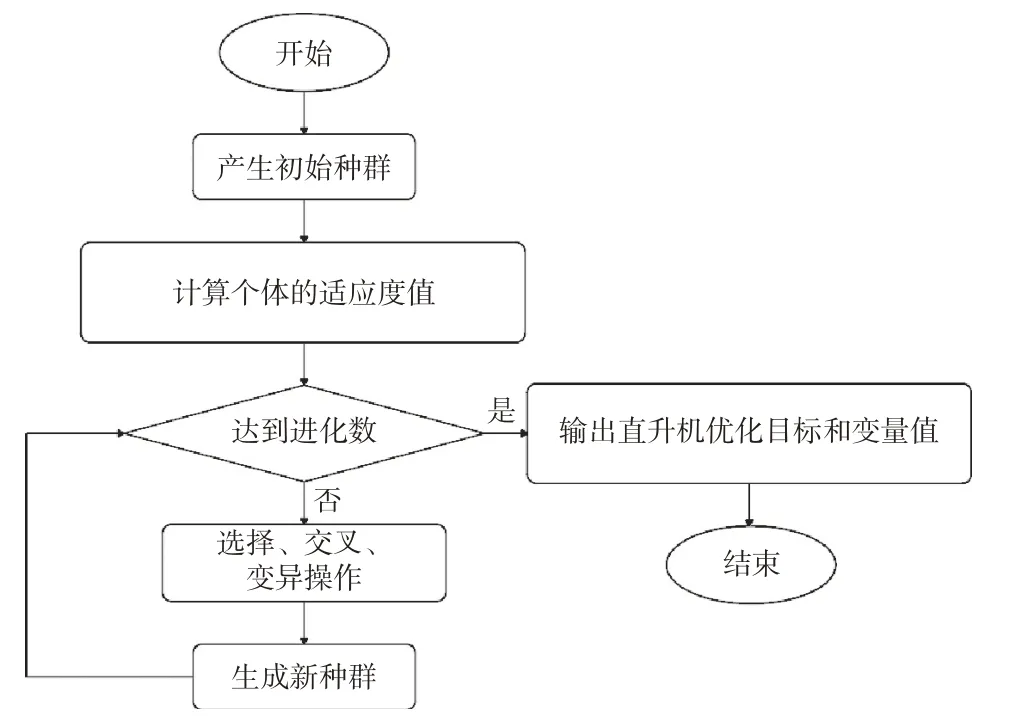
图4 复合式直升机性能优化流程Fig.4 Compound helicopter performance optimization process

3 复合式直升机性能优化结果与分析

为得到复合式直升机的最优功率,选取悬停阶段、低速阶段200km/h和高速阶段400km/h三个不同飞行状态分别进行基于遗传算法的性能优化。优化过程如图5所示,悬停、200km/h、400km/h下复合式直升机最优总功率随着迭代步数的增加而降低,基本在进化代数为40 时收敛。图6～图8 为悬停、200km/h 和400km/h 优化前后三种功率与样机基准值的对比。优化后三个不同飞行速度下对应的复合式直升机总功率、旋翼总功率、螺旋桨总功率均有降低。悬停、200km/h、400km/h优化后的直升机总功率比基准值要低16.3%、10.9%和19.6%。而旋翼的总功率分别降低了12.5%、10.3%和80.4%,其中对400km/h 优化后的旋翼从气流中吸收了大量能量,旋翼功率降低显著。三者优化后的螺旋桨总功率依次降低了22.9%、12.4%和6.7%。

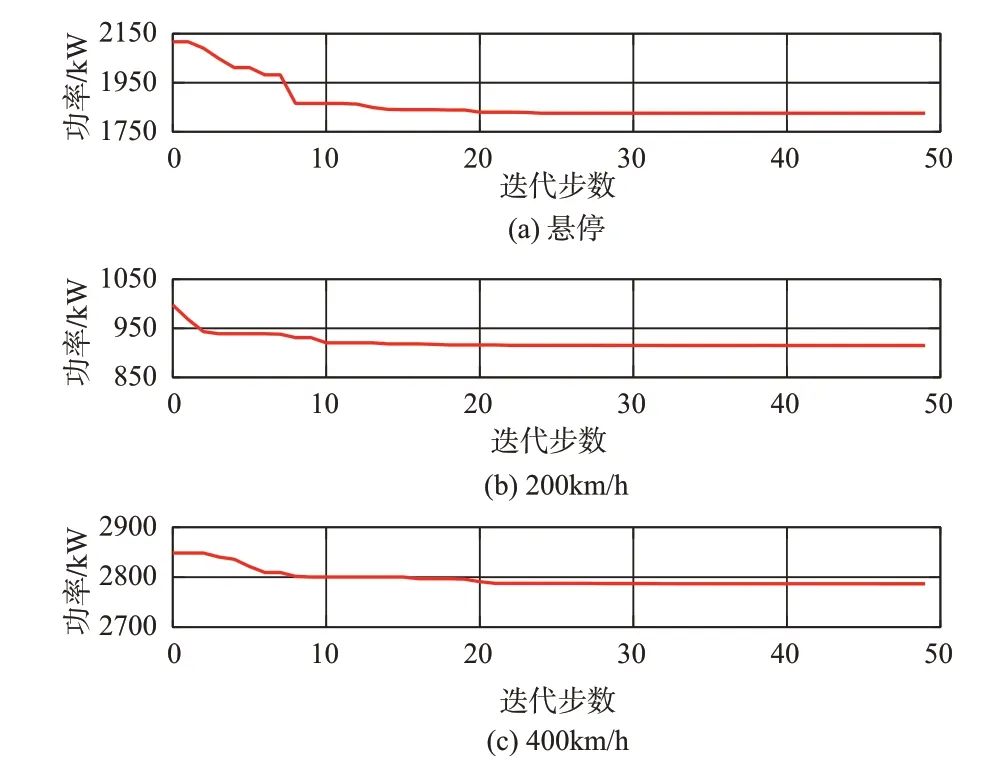
图5 悬停、200km/h、400km/h的性能优化过程Fig.5 Performance optimization process for hover,200km/h and 400km/h

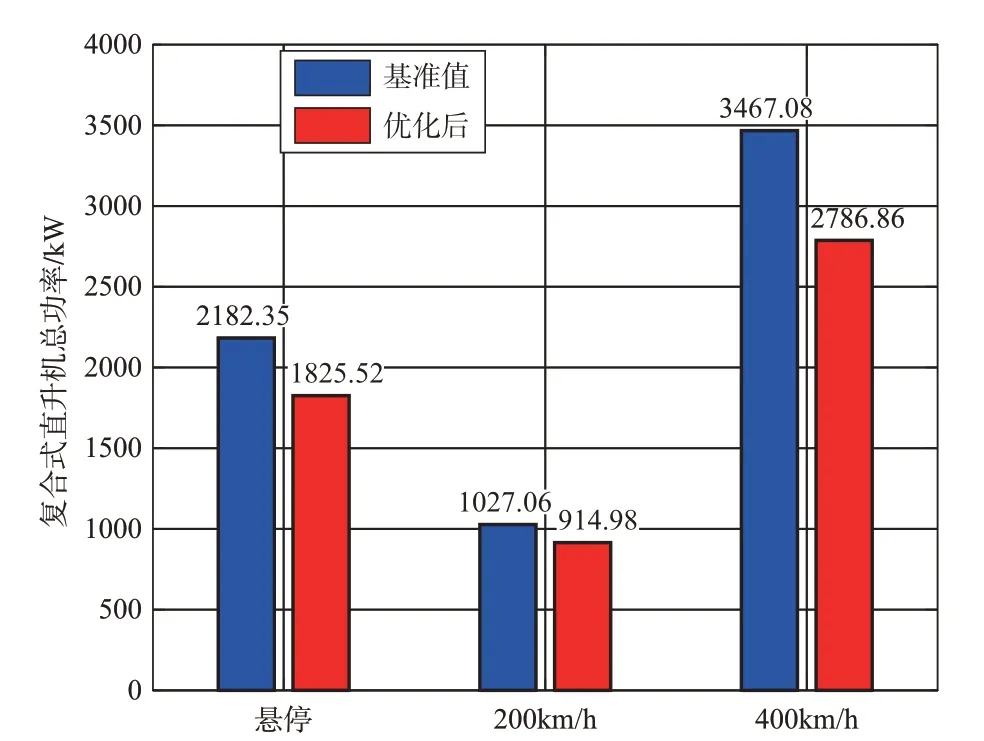
图6 优化前后悬停、200km/h、400km/h直升机总功率Fig.6 Total helicopter power before and after optimization of hover, 200km/h and 400km/h

表2 为悬停、200km/h、400km/h 优化前后对应的变量值。悬停时,诱导功率是旋翼和螺旋桨总功率的主要组成部分,悬停优化后旋翼和螺旋桨半径均增大并转速降低；200km/h 优化后的旋翼参数变化趋势与悬停相同,而螺旋桨参数变化趋势相反,机翼展长和面积增加；而高速时诱导功率小于型阻功率,400km/h 优化后旋翼和螺旋桨半径均减小但转速增大,机翼展长和面积减小。

图7 优化前后悬停、200km/h、400km/h旋翼总功率Fig.7 Total rotor power before and after optimization of hover,200km/h and 400km/h

图8 优化前后悬停、200km/h、400km/h螺旋桨总功率Fig.8 Total propeller power before and after optimization of hover, 200km/h and 400km/h

图9～图11 为0～450km/h 内,采用基准值与悬停、200km/h和400km/h优化变量值分别得到的直升机总功率、旋翼和螺旋桨总功率变化。复合式直升机在高速前飞时机体是保持水平姿态的,但由于悬停状态优化后机翼展长和面积显著增加,机翼产生了过多升力,使旋翼和机翼产生的总升力大于全机总重力,导致机体无法继续维持水平飞行,视为配平失败。因此,得到悬停状态优化后的直升机最大平飞速度仅为430km/h。由悬停状态下优化参数值得到的直升机总功率和旋翼总功率在低速阶段有很好的优化效果,功率节省率高于200km/h和400km/h。而采用400km/h优化参数值得到的直升机总功率和旋翼总功率在低速时均高于基准值,当速度超过350km/h 后总功率最低,功率节省率最高。速度为450km/h时,由400km/h优化值得到的直升机、旋翼总功率分别为3918.77kW、313.96kW,功率节省率为20.0%、67.8%,高于由200km/h 优化值得到的16.6%、35.0%。采用200km/h优化参数值得到的旋翼总功率在0～450km/h内均低于基准值,有全局优化效果,并且在高速时螺旋桨总功率优化效果最优。

表2 悬停、200km/h、400km/h优化前后对应的变量值Table 2 Variable values corresponding to before and after optimization of hover， 200km/hand 400km/h

图9 0～450km/h基准与优化变量值的直升机功率Fig.9 Total helicopter power at baseline and optimized variable values in 0～450km/h

图10 0～450km/h基准与优化变量值的旋翼总功率Fig.10 Total rotor power at baseline and optimized variable values in 0～450km/h

图11 0～450km/h基准与优化变量值的螺旋桨功率Fig.11 Total propeller power at baseline and optimized variable values in 0～450km/h

图12 和图13 给出了0～450km/h 内基准值与优化变量值得到的左右侧螺旋桨功率变化。当速度小于210km/h时,悬停的螺旋桨半径增加而转速降低,使得螺旋桨的诱导功率减小,左侧螺旋桨总功率降低,在100～200km/h范围内进入自转状态。而200km/h 和400km/h 优化后的螺旋桨半径减小,增大了悬停状态下的桨盘诱导速度,使得左侧螺旋桨开始进入自转状态时的飞行速度增加。右侧螺旋桨功率在低速时变化很小。速度超过210km/h 后,左右侧螺旋桨产生相等的正拉力,螺旋桨功率消耗随速度增加而增加,采用悬停、200km/h和400km/h优化参数值得到的螺旋桨功率均低于基准值。

图14～图16 给出了0～450km/h 内基准值与优化变量值下的总距、横向和纵向周期变距。低速时,机翼升力占比很小,由旋翼提供绝大部分升力,如图17 所示,由于对400km/h优化后得到的旋翼半径和悬停桨尖速度减小,因此为提供足够的拉力,采用400km/h优化参数值的旋翼总距显著增大,而悬停阶段优化后的则相反。由图17可得,速度大于210km/h 后,机翼升力随速度增加而快速增大,由于400km/h优化后的机翼面积和展长均减小,机翼产生的升力变小,机翼升力占比低于基准值,400km/h 的旋翼升力占比最大,故400km/h优化后旋翼总距依旧高于基准值。采用200km/h和400km/h优化参数值得到的横向周期变距在0～450km/h范围内基本比基准值要小。图16表明,速度超过210km/h后,由于左右螺旋桨均产生正拉力来提供飞行时的前进力,因此旋翼作用明显减弱,纵向周期变距会随速度增加而减小,高速时降至负值。图18 为旋翼的后倒角,当左右螺旋桨均产生正拉力时,旋翼桨盘由前倾变为后倒,此时螺旋桨除了克服机身阻力外,还需平衡旋翼向后的水平力。300km/h 时,采用400km/h 优化后的参数值得到的后倒角高于基准值,悬停、200km/h 优化后的后倒角比基准值要低。由图16 可得,这时三者优化后的纵向周期变距接近为0,意味着对400km/h 优化后的由吹风挥舞引起的桨盘后倒角更大。低速时,三者优化后的旋翼后倒角与基准值基本一致,但400km/h优化后由吹风挥舞造成的后倒角比基准值高,使得旋翼的纵向周期变距会相应增加。

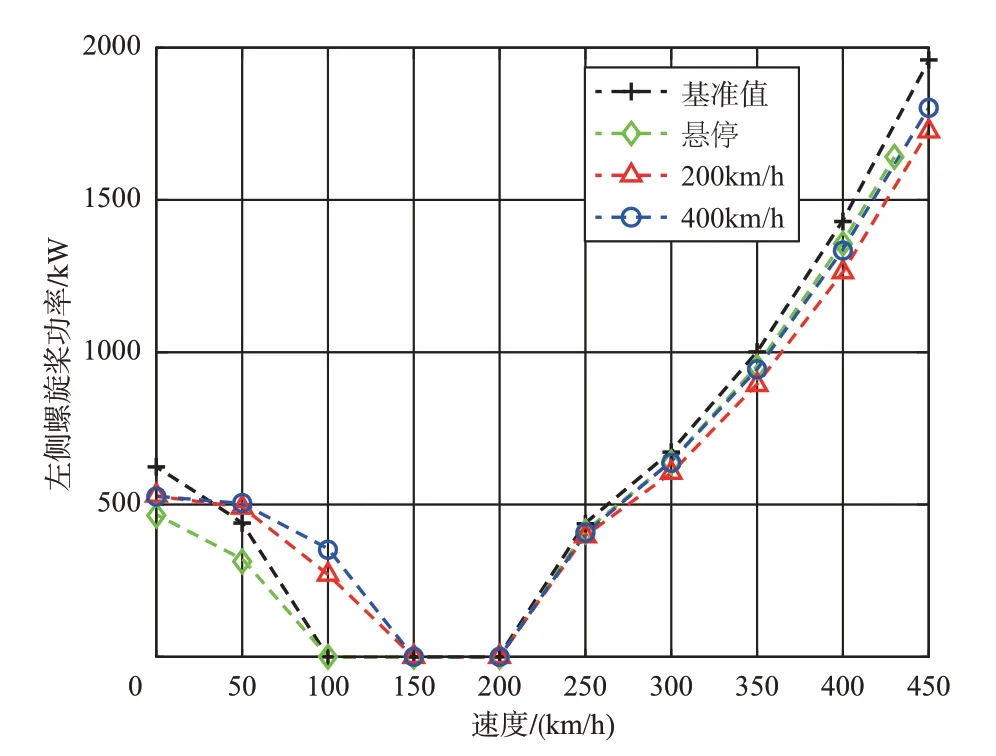
图12 0～450km/h基准值与优化变量值的左侧螺旋桨功率Fig.12 The left propeller power at baseline and optimized variable values in 0～450km/h

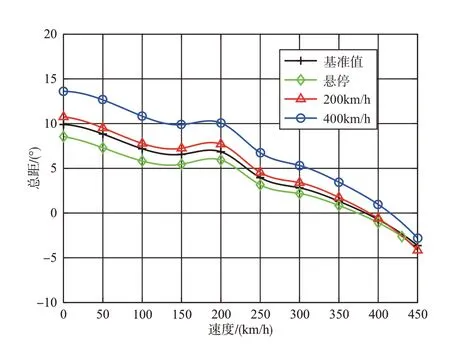
图14 0～450km/h基准值与优化变量值下的旋翼总距Fig.14 Collective pitch at baseline and optimized variable values in 0～450km/h

图15 0～450km/h基准值与优化变量值下的旋翼横向周期变距Fig.15 Lateral cyclic pitch at baseline and optimized variable values in 0～450km/h

图19 和图20 给出了0～450km/h 范围内基准值与优化变量值下的左右侧螺旋桨总距。低速时,由于左侧螺旋桨状态较为复杂,左侧螺旋桨总距变化较大。左右螺旋桨位于机翼翼梢处,因此低速时螺旋桨的拉力大小受旋翼反扭矩和机翼展长的影响。400km/h 优化后的旋翼反扭矩减小,但机翼展长也在减小,使得400km/h优化后的螺旋桨拉力比基准值大,并且优化后的螺旋桨半径减小,导致右侧螺旋桨的总距需要增加,左侧螺旋桨总距的变化趋势则相反。当左侧螺旋桨进入自转状态后,三者优化后的螺旋桨总距与基准值相近。速度大于210km/h 后,左右侧螺旋桨的总距相等,采用悬停、200km/h 和400km/h 优化参数值得到的螺旋桨总距均比基准值高。

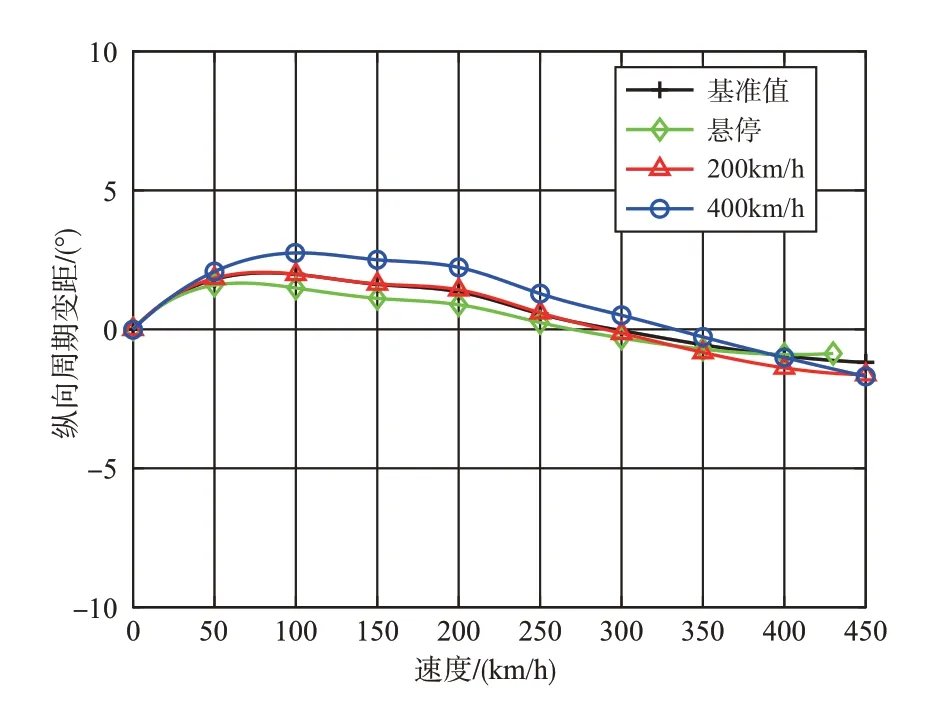
图16 0～450km/h基准值与优化变量值下的旋翼纵向周期变距Fig.16 Longitudinal cyclic pitch at baseline and optimized variable values in 0～450km/h

图17 0～450km/h基准与优化变量值的机翼升力占比Fig.17 Wing liftshare at baseline and optimized variable values in 0～450km/h

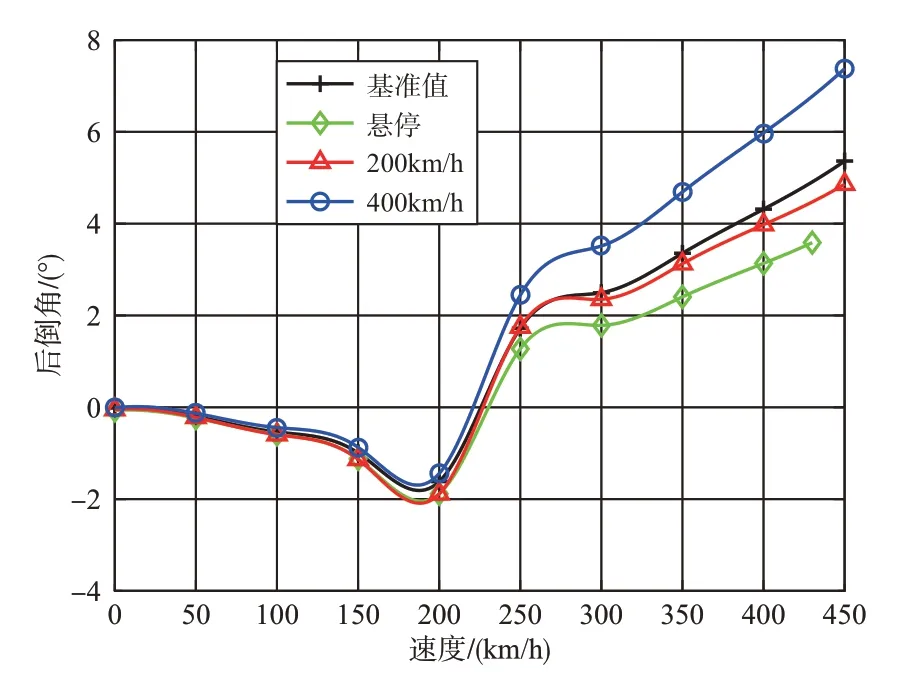
图18 0～450km/h基准值与优化变量值的旋翼后倒角Fig.18 The angle of backward tilt at baseline and optimized variable values in 0～450km/h

图19 0～450km/h基准值与优化变量值的左侧螺旋桨总距Fig.19 Collective picth of the left propeller at baseline and optimized variable values in 0～450km/h

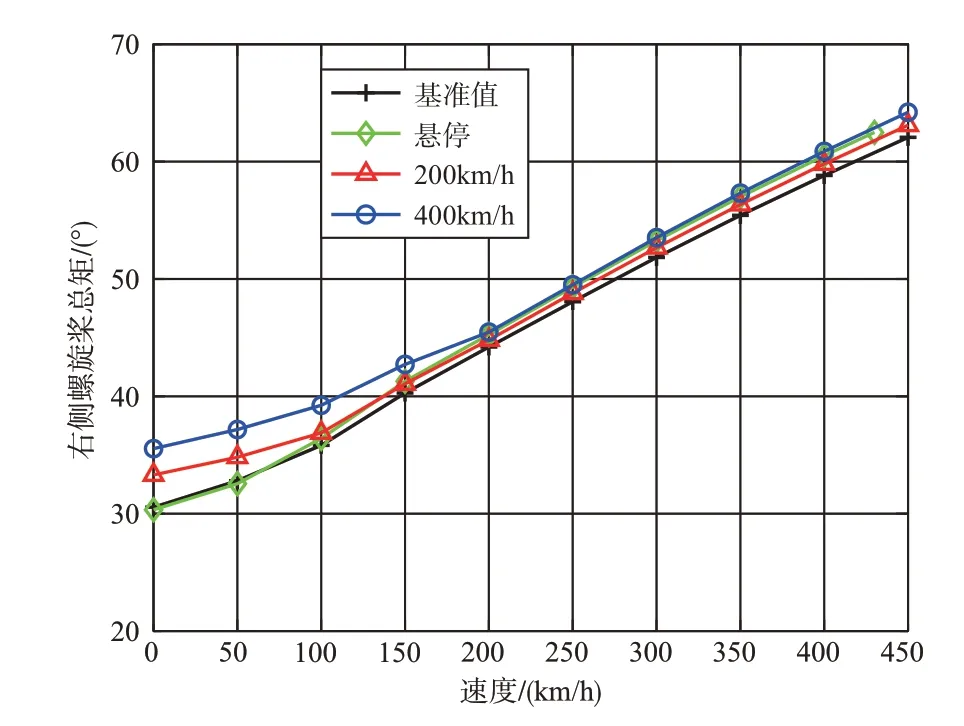
图20 0～450km/h基准值与优化变量值的右侧螺旋桨总距Fig.20 Collective picth of the right propeller at baseline and optimized variable values in 0～450km/h

图21～图22为0～450km/h范围内基准值与优化变量值下的机体俯仰角和滚转角。悬停、200km/h和400km/h优化后的俯仰角在0～450km/h内与基准值基本一致。速度小于210km/h时,通过机体低头和旋翼前倾提供前进推力,俯仰角随速度增加而增大,而后由螺旋桨提供前进力,机体接近水平。此时旋翼反扭矩由垂尾产生的侧向力平衡,图23给出250～450km/h范围内基准值与优化变量值下的垂尾侧向力变化。由于400km/h 优化后的旋翼反扭矩降低,垂尾需要提供的侧向力减小,机体滚转角会比基准值小,对悬停阶段优化后的滚转角则相反。

4 结论

图21 0～450km/h基准值与优化变量值的俯仰角Fig.21 Pitch angle at baseline and optimized variable values in 0～450km/h

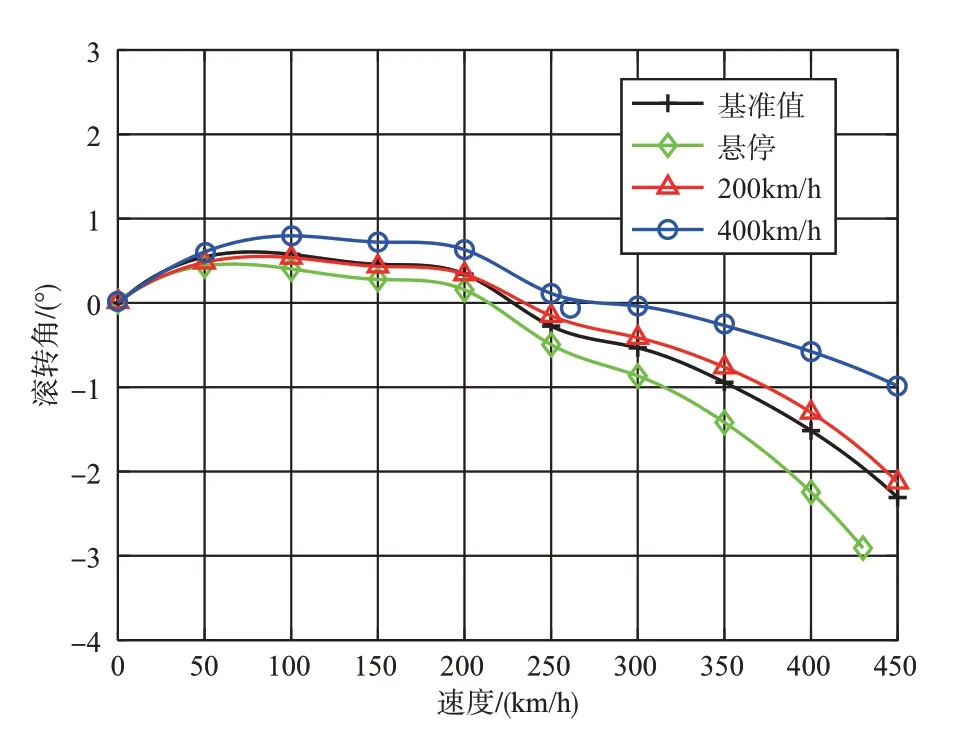
图22 0～450km/h基准值与优化变量值的滚转角Fig.22 Roll angle at baseline and optimized variable values in 0～450km/h

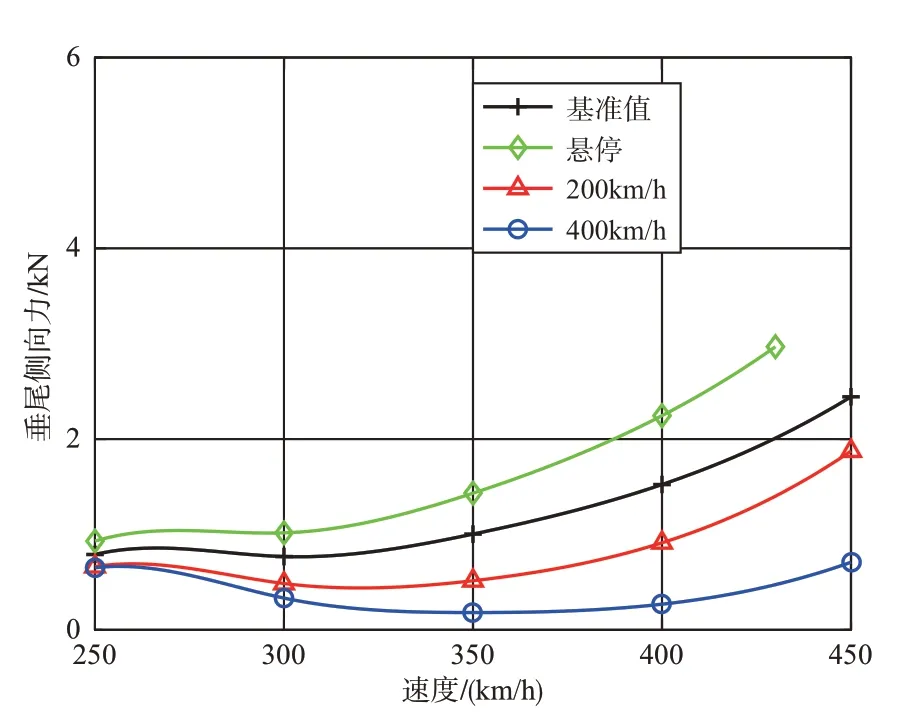
图23 250～450km/h基准与优化变量值的垂尾侧向力Fig.23 Lateral force of the vertical tail at baseline and optimized variable values in 250～450km/h

本文将Young 曲线拟合方法和动量叶素理论相结合,对悬停和低速阶段产生负向拉力的螺旋桨建立气动模型,以复合式直升机X3为样机构建了性能优化模型,分析了悬停、低速200km/h和高速400km/h三个不同飞行阶段优化前后的各类功率、操纵量和姿态角变化,给出了基于遗传算法的参数优化对常规复合式直升机飞行性能的影响规律,得到以下结论:

（1） 针对复合式直升机在特定飞行速度下的功率最优问题,采用基于遗传算法的参数优化方法是可行的。为兼顾高低速下的直升机性能,可选用加权的目标函数进行性能优化研究。

（2） 高速时最优直升机总功率主要依赖优化旋翼部件,通过显著降低旋翼总功率来实现。旋翼和螺旋桨半径均减小但转速增大,并配置更小的机翼是高速400km/h 的优化参数趋势。

（3）悬停状态的优化参数趋势和操纵量变化与400km/h优化后相反,而200km/h优化后的旋翼参数变化趋势与悬停状态一致,螺旋桨参数变化趋势则相反。三者优化后的俯仰角在0～450km/h范围内与基准值基本一致,在螺旋桨均提供正拉力后机体为水平姿态但旋翼桨盘会后倒。