基于改进认知可靠性与失误分析方法的隧道驾驶人因可靠性分析模型

2023-09-27施金斌刘晓佳马国旺唐慧漪

科学技术与工程 2023年25期

施金斌, 刘晓佳*, 马国旺, 唐慧漪

(1.集美大学航海学院, 厦门 361021; 2.集美大学海上交通安全研究所, 厦门 361021)

近年来,随着中国经济的快速发展,人均车辆保有量及交通需求量与日俱增,中国隧道总里程也在不断增加,截至2020年末,全国公路隧道为21 316处,全长2 199.93万m[1]。与此同时,隧道交通安全问题日益显现[2]。隧道具有道路情况复杂、封闭的特点,一旦发生事故,后果往往非常严重。不仅造成相应的经济损失,更会产生生命威胁。据统计,隧道交通事故死亡率为0.48人/起,是同期全部事故死亡率的1.6倍[3],如何减少隧道交通事故已成为急需解决的问题。隧道交通事故产生的原因众多,其中最主要的便是人的因素,研究表明近89%的隧道事故与人因因素有关[4],多数事故的原因包括驾驶人的感知、判断或操作的差错。在驾驶过程中,驾驶人通过视觉获取的交通信息占90%,然而在通过隧道时,驾驶人的空间辨识距离变短,观察能力下降,极易发生事故。因此研究驾驶人在通过隧道时的人因可靠性十分重要,对道路交通安全研究具有重大意义。

人因可靠性分析(human reliability analysis,HRA)是安全领域的重点研究对象。第二代HRA方法包括认知可靠性与失误分析方法(cognitive reliability and error ana-lysis method,CREAM)、人员执行型错误分析方法(a technique for human error analysis,ATHEANA)等。其中最典型的是CREAM方法,该方法已在核电、航空航天、海事等领域[5-6]得到了广泛运用。马昕晖等[7]通过模糊方法处理共用绩效条件(common performance condition,CPC)与控制模式之间的映射关系,建立适用于航天发射场的人因分析模型,从而计算任务的人因失误概率。席永涛等[8]采用CREAM方法,结合模糊集合、证据推理及贝叶斯网络,量化分析不确定信息条件下的船舶驾驶员人因可靠性。杨越等[9]通过CREAM扩展法,建立管制行为形成因子与情景控制模式的不确定关系模型,预测管制员的人误概率。王彦富等[10]从解决CREAM模型中存在的任务环境与控制模式离散化问题出发,改进预测方法,成功预测海洋平台火灾爆炸风险的人误概率。然而CREAM方法在汽车驾驶中的应用较少,且驾驶人通过隧道时的情景环境与核电、海事、航天航空存在较大差距,不能直接应用于驾驶人通过隧道的人因可靠性分析。赖永明等[11]将CREAM回溯分析法与预测分析法相结合,构建公路驾驶领域的人因可靠性分析模型,提高了人误概率预测的准确性。目前隧道安全研究以隧道施工安全为主,现以隧道内行驶的驾驶人为研究对象,研究隧道驾驶人因可靠性。提出一种改进的CREAM模型,结合贝叶斯网络技术,计算人因失误概率。首先根据隧道驾驶任务特点对CPC因子进行改进,使用模糊逻辑方法将先验条件概率从确定值转换为概率值,同时考虑CPC因子间的相互影响,结合贝叶斯网络技术,计算驾驶人的人因失误概率,为后续隧道驾驶的人因分析提供依据。

1 CREAM方法

CREAM[12]方法由Hollnageal于1998年建立,其指出人在各项活动中的行为与环境紧密相连,不是孤立存在。CREAM方法包括9种CPC因子,分别为:组织因素、工作条件、人机界面和操作支持、规程/计划的可用性、同时出现的目标数量、可用时间、工作时间、培训和实践经验培训、班组成员的合作质量。每个CPC因子划分的等级有所不同,对期望效应产生改进、不显著、降低3种不同的影响。CREAM通过CPC因子体现人完成任务时所处的情景环境,结合期望效应,最终确定人因控制模式,即战略型、战术型、机会型和混乱型。

CREAM方法起源于核电领域,在核工业、航空航天等领域已有广泛运用,但与交通领域存在较大差异,因此原方法提出的CPC因子并不完全适用于隧道驾驶人因分析领域,需结合隧道驾驶特点进行调整。同时原方法并未给出各因子的详细评估因素,在实际操作中主观性较强,需给出各CPC因子的评估细则。基于以上讨论,结合CREAM基本法,通过统计分析隧道驾驶事故产生的原因,根据实际情况结合专家意见,对原CPC因子进行调整,给出每个因子的评估细则。最终确定9种CPC因子,分别为CPC1组织因素、CPC2工作负荷、CPC3人机界面与支持程度、CPC4行车环境、CPC5情景感知、CPC6内部驾驶环境、CPC7行车时间、CPC8个人心理生理状态、CPC9技能和经验,并给出说明,如表1所示。

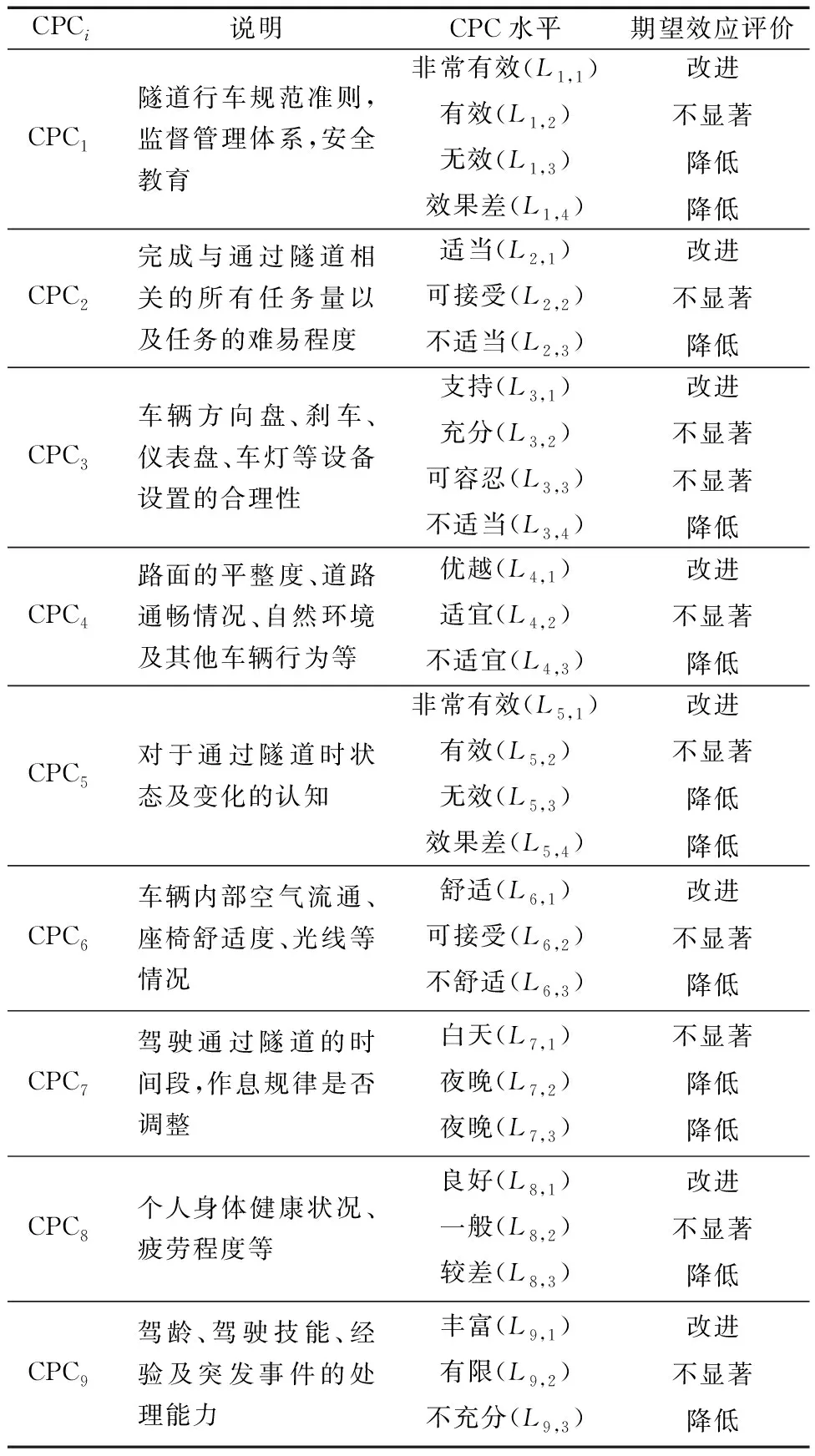
表1 改进后的CPC及描述Table 1 Improved CPC and its description

CREAM分为基本法与扩展法两种,基本法观察CPC因子的评价水平,分别记录改进、不显著和降低的CPC因子数量,改进为正效应,不改进为负效应。然后根据正负效用的CPC因子数量,确定在该环境下所处的人因失误模式。改进后的人因失误模式如图1所示。

图1 CREAM基本法控制模式图Fig.1 Control mode diagram of CREAM fundamentals

2 改进CREAM模型的建立

2.1 CPC因子的模糊化

模糊化即将一个系统的离散语言转化为模糊集合的形式。模糊集合与普通集合不同,通过隶属度函数来描述对象的全体,每个区间的隶属度取值范围为[0,1]。在CREAM基本法中,每个CPC因子仅存在3～4个评价等级,因子的影响都是离散和确定的,即0%或100%,区分度过小,因此需要对其进行模糊化处理,将系统的离散输入量转化为连续值。选定CPC因子模糊集的论域为[0,100][13],将其转化为模糊输出。由于CPC7仅有“夜晚”和“白天”两个区间,为方便计算,对应论域更改为[0,24],且新增一个“夜晚”区间,改进后的CPC模糊集如表2所示。

表2 改进后的CPC模糊集Table 2 Improved CPC fuzzy set

然后通过隶属度函数将CPC因子的连续值转换为概率值,隶属度函数包括三角形、梯形、高斯形、钟形等。三角形隶属度函数具有运算简便、形状简单等特点,且在性能方面与其他复杂的隶属度函数差距较小,因此选择三角形隶属度函数。其中3个模糊子集与4个模糊子集的隶属度函数有所区别,如式(1)～式(3)所示。

3个模糊子集的隶属度函数表达式为

(1)

行车时间的隶属度函数表达式为

(2)

4个模糊子集的隶属度函数表达式为

(3)

2.2 模糊规则的建立及CPC因子的调整

模糊规则的建立依赖于CREAM方法自身的逻辑,CPC因子的模糊输入与控制模式的模糊集通过模糊规则建立。建立单输入-多输出的模糊IF-THEN规则[14],其中输入为CPC因子,输出为人因失误的控制模式。为简化表达,对9种CPC因子进行编号,如表1所示。控制模式编号为:战略型D1、战术型D2、机会型D3、混乱型D4。模糊规则可表示为

IFL1,mANDL2,mAND…ANDL9,m,THEN

(4)

举例说明如下。

Rk:若“组织因素”为无效(L1,3),“工作负荷”为可接受(L2,2),“人机界面与支持程度”为支持(L3,1),“行车环境”为优越(L4,1),“情景感知”为效果差(L5,4),“内部驾驶环境”为舒适(L6,1),“行车时间”为白天(L7,1),“个人心理生理状态”为良好(L8,1),“技能和经验”为丰富(L9,1)。那么驾驶员的控制模式将为50%置信度的战术型及50%置信度的机会型。

可用公式表示为

IFL1,3ANDL2,2ANDL3,1ANDL4,1ANDL5,4

ANDL6,1ANDL7,1ANDL8,1ANDL9,1,THEN

{(0,D1),(0.5,D2),(0.5,D3),(0,D4)}

(5)

在现实中,CPC因子之间并不是独立存在的,因子间存在着相互依赖的关系。一个CPC因子的评估水平会受到一个或者多个CPC因子的影响,如驾驶人的情景感知会受到行车环境、行车时间、个人生心理状况等因素的影响。为实现对驾驶人经过隧道时的人因可靠性更为精确的分析,需要对其进行调整[15]。列出可能需要调整的CPC因子,及其所依赖的其他因子,如表3所示。

表3 CPC因子调整规则Table 3 CPC adjustment rules

调整规则如下。

(1)若CPC2的初始评价水平为不显著,CPC3、CPC4和CPC8中有任意2个及以上因子的评价水平为(改进/降低)时,那么CPC2的评价水平调整为(改进/降低)。

(2)若CPC4的初始评价水平为不显著,CPC1、CPC3、CPC7和CPC9中有任意3个因子的评价水平为(改进/降低)时,那么CPC4的评价水平调整为(改进/降低)。

(3)若CPC5的初始评价水平为不显著,CPC1、CPC4、CPC7、CPC8和CPC9中有任意4个因子的评价水平为(改进/降低)时,那么CPC5的评价水平调整为(改进/降低)。

(4)若CPC8的初始评价水平为不显著,CPC1、CPC4和CPC6中有任意2个及以上因子的评价水平为(改进/降低)时,那么CPC8的评价水平调整为(改进/降低)。

CPC因子之间的相互影响关系,如图2所示。

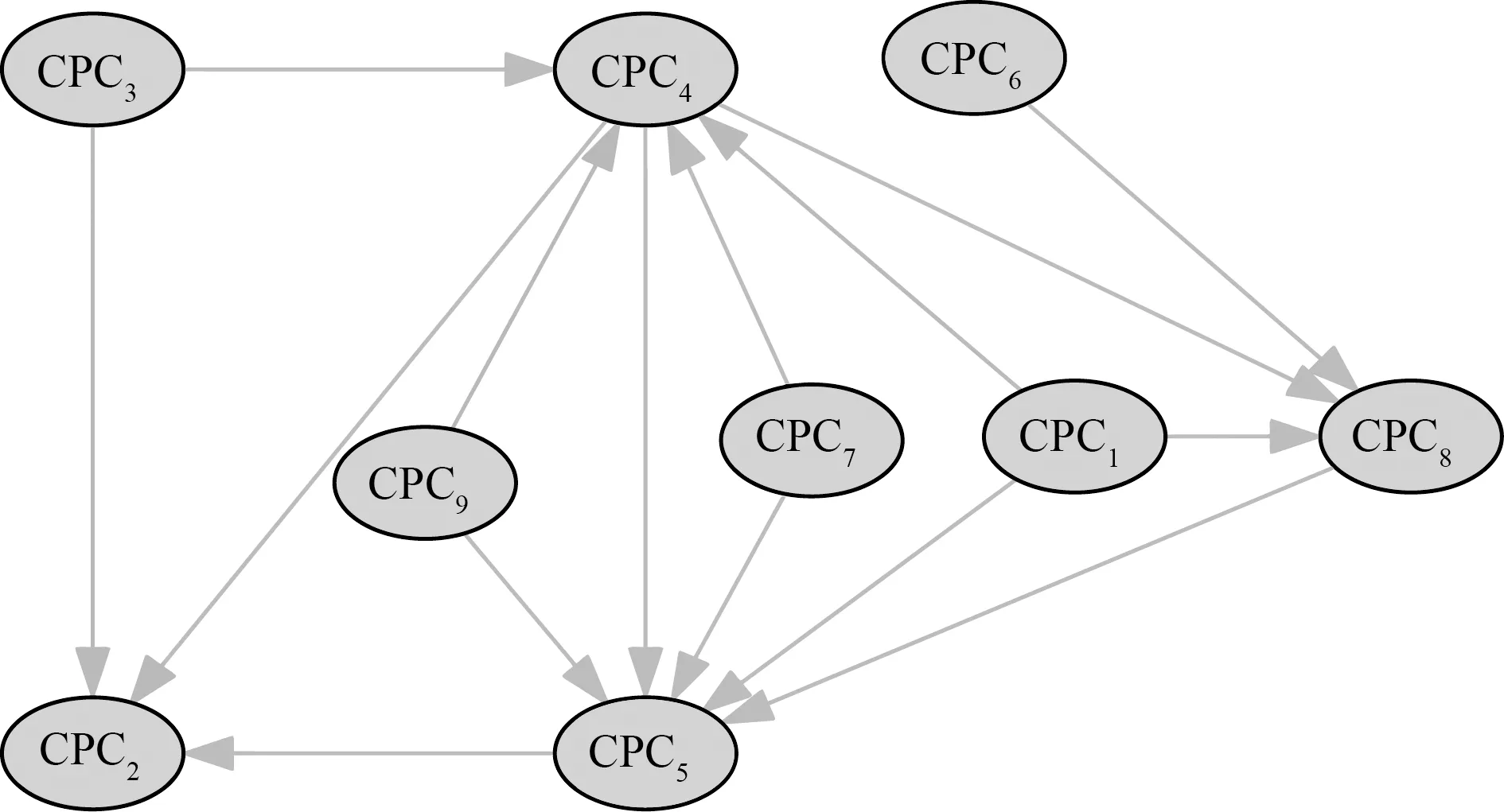
图2 CPC因子相互影响关系图Fig.2 CPC interaction diagram

2.3 贝叶斯网络技术建模

使用贝叶斯网络技术对IF-THEN规则库进行建模,可用条件概率进行表示,Rk可以转化为

P(Dj|L1,3,L2,2,L3,1,L4,1,L5,4,L6,1,L7,1,L8,1,

L9,1)=(0,0.5,0.5,0)

(6)

改进后的CREAM方法中有4个CPC因子的水平等级为4种,5个CPC因子的水平等级为3种,根据IF-THEN规则,共有44×35,共计62 208条条件概率用以构建网络,然而过多的条件概率会导致工作量巨大。因此使用分离方法,在CPC因子与控制模式之间加入3个辅助节点,以减少父节点的数量。第一组A1包括CPC1、CPC2、CPC3;第二组A2包括CPC4、CPC5、CPC6;CPC7、CPC8、CPC9则包含于第三组A3,如图3所示。

将CPC因子与控制模式转化为贝叶斯网络的形式,其中父节点为CPC因子,子节点则为人因控制模式,记子节点为ND。然后,基于IF-THEN规则的人误概率分析推理,简化为计算子节点ND的概率,公式为

(7)

则根据贝叶斯网络原理可知节点ND的概率为

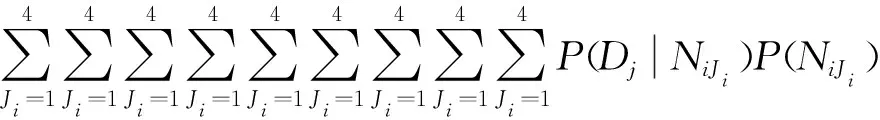
(8)

2.4 人因失误概率计算

根据上述步骤得到的控制模式结果,可以计算给定场景下的人因失误概率(human error probability,HEP),HEP越低,则人因可靠性越高。此时依据图1中人因控制模式的人误概率区间确定通用人误概率值UDj。首先,模糊化处理4个控制模式,通过最大加权平均值计算UDj的值。在隶属度为1的情况下,相对应的概率值的对数表示为{-3.65,-2,-1.12,0.5},统一去对数后得{2.24×10-4,0.01,0.070 8,0.316},用以进行基准测试,可知HEP的计算公式为

(9)

3 实例分析

3.1 实例及数据处理

为了验证模型对驾驶人通过隧道时人因可靠性分析的适用性,选定驾驶人通过厦门市梧村隧道进行研究。梧村隧道是目前国内最长的城市公路隧道,全长3.7 km,极大地缩短了厦门火车站至机场的通行时间,交通流量大,隧道较长,交通事故时有发生。研究时间为2022年4月16日,厦门市天气晴朗,微风。汽车人机交互界面具有充分适当性,驾驶人驾龄6年。

邀请5位隧道及人因领域专家,通过专家打分法对驾驶人通过隧道任务的CPC因子进行0～100打分,取平均值。此处使用5级李克特量表进行评分,通过隶属度函数将分值转换为概率值,结果如表4所示。

表4 CPC绩效效应值Table 4 CPC performance effect value

考虑CPC因子间的相互影响,以CPC因子调整规则1为例。已知CPC2的评价水平,其所依赖的因子CPC3为{改进(15%),不显著(85%),不显著(0%),降低(0%)},CPC8为{改进(20%),不显著(80%),降低(0%)}时,可知CPC3与CPC8评价水平中“改进”的重叠部分占15%。此时CPC2评价水平中“不显著”为100%,故其评价水平中“改进”部分更改为15%,剩余的85%不满足调整规则1,保持不变。最终CPC2的评价水平更改为{改进(15%),不显著(85%),降低(0%)},用概率值表示为0.15L2,1和0.85L2,2,同理可得CPC4、CPC5、CPC8调整后的概率值。

依据改进的CREAM模型,运用GeNIe软件对CPC因子的绩效效应值进行处理,从而确定驾驶人完成隧道驾驶任务的控制模式,如图3所示。结合式(9),可以计算驾驶人通过隧道时的人因失误概率,具体计算过程为

HEP=0.08×2.24×10-4+0.75×0.01+0.17×0.070 8+0=1.955×10-2。

3.2 结果分析

采用传统CREAM方法分析,仅可获知驾驶人在完成通过隧道任务时的控制模式为“战术型”,人因失误概率为0.001～0.1,概率区间过大。采用改进的CREAM方法所得到的人因失误概率为1.955×10-2。改进后的模型较传统方法能够更加精确地计算人因失误概率。

使用灵敏度分析方法,验证改进后模型的有效性。对CPC1的分值进行以10为增量的改变,经过计算可知,当CPC1分值为66时,人因失误概率为1.943×10-2。当CPC1分值为46时,人因失误概率为1.961×10-2。由结果可知,当CPC因子分值增大时,人因失误概率会降低,当CPC因子分值减少时,人因失误概率随之增大,从而验证了模型的有效性。