基于ARIMA-LSTM-XGBoost组合模型的铁路货运量预测

2023-09-27龙宇许浩然余华云何勇徐红牛

科学技术与工程 2023年25期

龙宇, 许浩然, 余华云, 何勇, 徐红牛

(长江大学计算机科学学院, 荆州 434023)

铁路货运是中国经济的重要组成部分,为中国经济发展提供了强大的动力。特别是在大宗货物如钢铁、金属矿石、原煤等的运输上,铁路货运方式占据了极大的比重。近年来进出口贸易不断发展,同时,在“一带一路”“公转铁”等政策的推动下,发展铁路货运成为中国经济转型、实现绿色发展的战略性举措[1]。因此准确预测铁路货运量对规划铁路货运线路、调整铁路运输结构、优化铁路货运资源配置等方面具有重要的意义。

目前在铁路货运量预测研究领域,预测研究方法可以分为单一预测模型和组合预测模型。单一预测模型可分为时间序列分析方法和机器学习方法两类,时间序列分析方法有移动平均自回归模型、差分整合移动平均自回归模型、指数平滑法、季节指数预测法等;机器学习方法有支持向量机、随机森林、神经网络、灰色预测方法、极限梯度提升等。组合预测模型可以融合单一模型的优势,提升预测精度。常用的组合预测方式有误差修正型组合模型、数据预处理型组合模型、权重分配性组合模型。

徐莉等[2]提出残差二次修正的方法,基于GM(1,1)预测模型,在对残差进行一次修正的基础上,进行残差二次修正,提高了模型预测精度。程肇兰等[3]建立基于长短时间记忆(long short-term memory,LSTM)神经网络的铁路月货运量和日货运量预测模型,结果表明,同差分整合移动平均自回归模型(autoregressive integrated moving average,ARIMA)模型和BP神经网络模型相比,LSTM网络预测效果更优。李万等[4]提出基于粒子群算法优化的LSTM神经网络(IPSO-LSTM)预测模型,通过粒子群算法优化(improved particle swarm optimization,IPSO)进行LSTM网络参数优化,验证了该预测模型的可行性。Guo等[5]采用遗传算法搜索广义回归神经网络(general regression neural network,GRNN)的最优扩散,并将其应用于GRNN中进行铁路货运量预测。结果表明,遗传算法优化的GRNN预测精度更高。邵梦汝等[6]构建灰色预测模型和BP神经网络模型组合的灰色-神经网络组合模型,验证了组合模型能够提高模型预测准确率。徐玉萍等[7]利用误差修正法将引入注意力机制的LSTM模型与乘积季节模型组合进行铁路货运量预测,结果表明组合模型精度高于单一预测模型。耿立艳等[8]提出基于果蝇算法(fruit fly optimization algorithm,FOA)优化混合核最小二乘支持向量机(least squares support vector machine,LSSVM)的预测方法,提升了计算速度和预测精度,适合进行短期预测。

可见目前对于铁路货运量预测已有大量的研究,且研究方法和改进方式各有特点,上述单一预测模型和组合预测模型未充分考虑到铁路货运量序列中体现出的线性特征和非线性特征,同时在进行参数改进时寻求局部最优解可能会存在模型过拟合、泛化能力较弱的问题。

自回归移动平均模型(ARIMA)能够较好地拟合预测时间序列中的线性特征,长短期记忆神经网络(LSTM)能够学习长期行为,善于处理长时间时间序列预测问题,且具有较强的非线性特征处理能力[9]。机器学习模型极端梯度提升(extreme gradient boosting, XGBoost)模型通过添加正则项防止过度拟合,同时提高模型泛化能力[10]。

现将ARIMA、LSTM、XGBoost模型组合,提出基于ARIMA-LSTM-XGBoost的加权组合模型。先使用ARIMA模型拟合序列中的线性特征,再使用LSTM神经网络校正ARIMA模型预测残差,以此拟合序列中的非线性特征,再与XGBoost模型预测结果结合,使用误差倒数法确定权重进行组合预测以减小误差。最后将组合预测模型同单一模型预测结果进行对比分析,验证组合模型预测铁路货运量的有效性。

1 研究方法

1.1 ARIMA模型

差分整合移动平均自回归模型(ARIMA)是自回归滑动平均模型(ARMA)和差分性的结合[11]。

自回归滑动平均模型ARMA(p,q)模型表达式为

(1)

式(1)中:Yt为t时间点时间序列值;p为自回归项数;q为滑动平均项数;αi为自回归模型的系数;θi为滑动平均模型的系数;εt为白噪声序列;C为常数。

ARMA(p,q)模型只能用于预测相对平稳的时间序列数据,对于非平稳时间序列需要进行d阶差分使序列平稳后再进行处理,由此可以得到ARIMA(p,d,q)模型。

ARIMA模型建立与数据预测过程包括以下4个步骤[12]。

步骤1白噪声检验和平稳性检验。

检验序列是否是白噪声序列。若序列是白噪声序列,变量之间没有相关性,无法提取出数据的有效特征。

检验序列是否具有平稳性,若序列不平稳,须通过差分运算将其转化为平稳序列[13]。

步骤2模型参数选择。

确定ARIMA(p,d,q)模型中p、d、q3个参数,参数d为差分的阶数。绘制自相关函数图像和偏自相关函数图像,通过观察图像,确定参数p和q可能的取值,再结合赤池信息准则(Akaike information criterion,AIC)或贝叶斯信息准则(Bayesian information criterion,BIC)选择使模型最优的参数。

步骤3模型检验。

对模型残差序列进行白噪声检验,验证序列是否具有相关性。同时检验残差序列是否符合正态分布以验证模型的适用性。

步骤4数据预测。

根据数据集中历史数据预测未来时刻数据。

1.2 LSTM神经网络

循环神经网络(regression neural network,RNN)是一种拥有输入层-隐藏层-输出层结构的典型神经网络,其隐藏层的输入不仅包括输入层的输入,还包括上一时刻隐藏层的输出。这种结构使得RNN不仅会记忆当前时刻的信息,还会记忆前面的信息并作为输入信息参与当前运算。其在拟合非线性时间序列时有良好的性能,但在实际应用中,RNN在解决长期依赖问题时有所欠缺,在随时间反向传播期间会存在梯度消失的问题。为了解决这个问题,Hochreiter等[14]提出了长短时间记忆神经网络(LSTM)。相对于RNN,LSTM在其隐藏层中添加了遗忘门、输入门、输出门3个门层,其隐藏层结构图如图1所示。

图1 LSTM隐藏层结构图Fig.1 Structure diagram of LSTM hidden layer

遗忘门决定从上一时刻细胞状态中丢弃和保留的信息。输入信息为上一时刻隐藏层信息ht-1和当前时刻输入数据xt,通过遗忘门确定保留的信息范围,公式为

ft=σ(Wf[ht-1,xt]+bf)

(2)

式(2)中:ft为t时刻遗忘门的输出信息;Wf为遗忘门权重系数;bf为遗忘门偏置系数;σ为sigmoid激活函数。

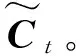
it=σ(Wi[ht-1,xt]+bi)

(3)

(4)

式中:it为t时刻输入门的输出信息;Wi为权重;bi为输入门偏置系数;σ为sigmoid激活函数;bC为细胞状态门控单元偏置系数。

将上一时刻记忆信息Ct-1与遗忘门输出ft相乘决定需要丢弃和保留的信息,再加上输入门所得的候选记忆信息,得到新的细胞状态Ct,其计算公式为

(5)

输出门根据输入值和记忆单元确定当前记忆状态Ct的输出信息,将输入信息先通过输出门确定输出范围,再把细胞状态通过一个tanh函数进行处理,经输出门确定输出信息ht。

ot=σ(Wo[ht-1,xt]+bo)

(6)

ht=ottanh(Ct)

(7)

式中:ot为t时刻输出门的输出信息;Wo为权重;bo为输出门偏置系数;σ为sigmoid激活函数。

1.3 XGBoost模型

极端梯度提升模型(XGBoost),是一种基于boosting集成的树模型,对梯度提升决策树(gradient boosting decison tree,GBDT) 进行优化,通过添加树、不断地进行特征分裂生成新树的方式,拟合前一棵树的预测误差,以此来提升预测精度[15]。

XGBoost模型表达式为

(8)

XGBoost算法的目标函数为

(9)

(10)

正则项计算公式为

(11)

式(11)中:γ为控制叶子数量参数(惩罚系数);T为叶子节点数;λ为正则项参数;ωj为第j个叶子节点的权重。

最终目的是找到使目标函数Obj(t)最小的ft。在ft=0处进行泰勒二阶展开,得到的目标函数近似于

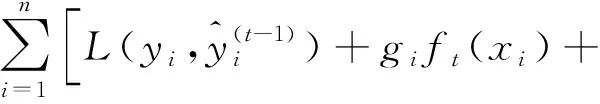
(12)

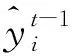
结合式(11)和式(12),可求得最优的w和目标函数为

(13)

(14)

1.4 组合预测模型

为提升模型的预测精度和泛化能力,采用基于误差修正和基于权重分配的组合方式对ARIMA模型、LSTM模型、XGBoost模型进行组合,组合模型结构图如图2所示。

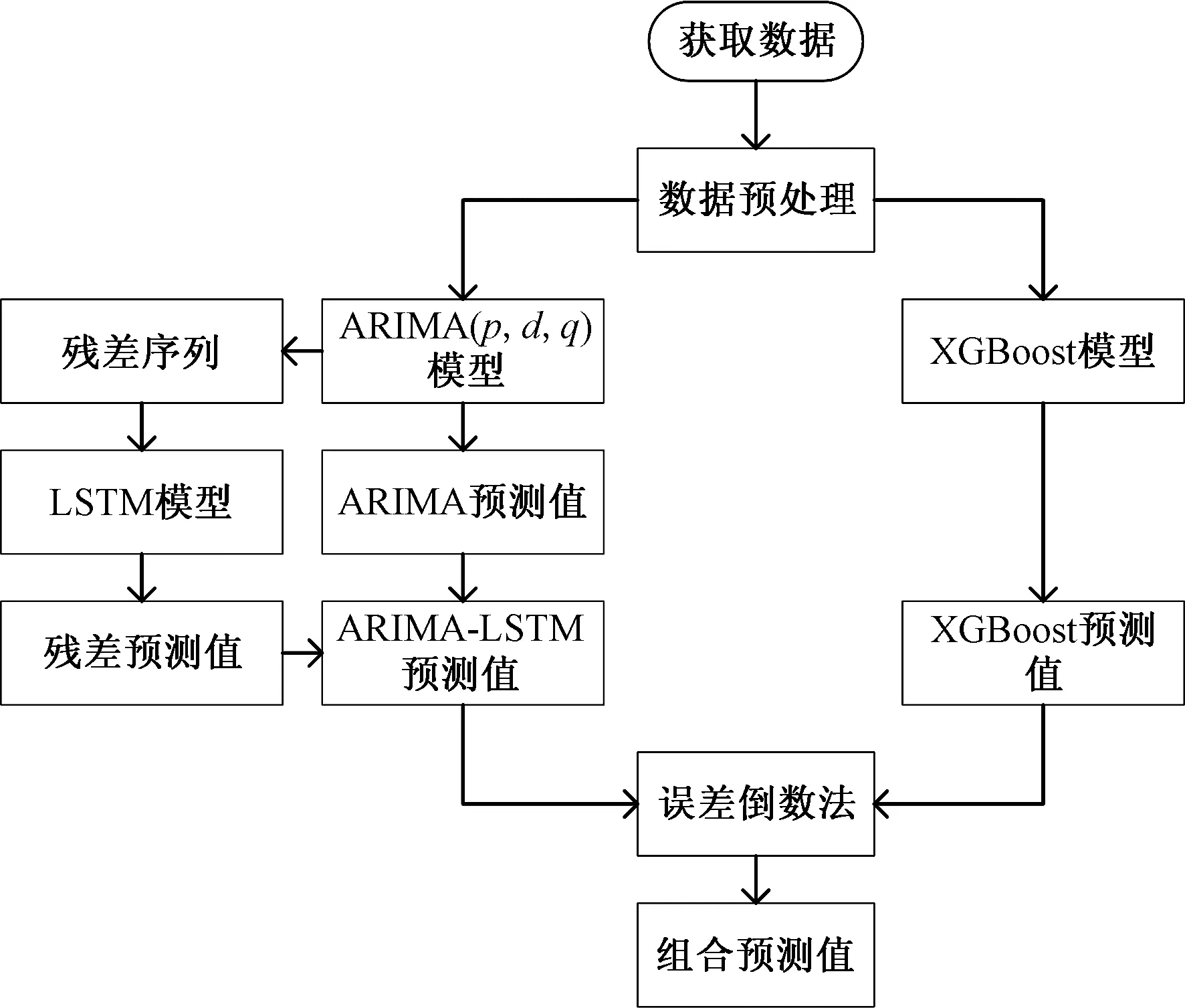
图2 组合模型结构图Fig.2 Structure diagram of combination model

1.4.1 基于误差修正型的组合方式

结合传统时间序列模型和神经网络模型的优点,构造了一种基于误差修正型的组合模型ARIMA-LSTM。

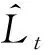
(15)

(16)

1.4.2 基于权重分配型的组合方式

使用误差倒数法为模型赋予权重进行加权组合,使用此方法将误差较小的模型赋予较大的权重,可以显著降低组合模型的总体误差。

(17)

(18)

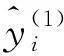
(19)

1.5 模型评价指标

为评估模型预测效果,采用均方误差(mean square error,MSE)、均方根误差(root mean squared error,RMSE)、平均绝对值误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)作为评价指标,各评价指标计算公式如下。

(1)均方误差MSE。

(20)

(2)均方根误差RMSE。

(21)

(3)平均绝对值误差MAE。

(22)

(4)平均绝对百分比误差MAPE。

(23)

2 模型建立和实验分析

2.1 数据获取

从国家统计局官网收集2007年1月—2021年12月的全国铁路货运量月度数据集,每条数据包括对应的月份以及铁路货运量数值。数据如图3所示。

图3 2007年1月—2021年12月铁路货运量时序图Fig.3 Sequence diagram of railway freight volume from January 2007 to December 2021

2.2 ARIMA模型建立

使用ARIMA模型对铁路货运量时间序列数据进行初步预测,模型建立步骤如下。

2.2.1 序列特征检验和模型定阶

对铁路货运量序列进行白噪声检验,检验统计量P=4.52×10-29<0.05,说明该序列非白噪声序列。

采用迪基-福勒(augmented Dickey-Fuller test, ADF)检验方法[18]来判断序列是否具有平稳性,显著性水平P=0.836 2>0.05,可见原始序列ADF检验没有通过显著性检验,说明该序列不平稳。

对该序列做一次差分运算,对一阶差分序列进行白噪声检验,检验统计量P<0.05,可知一阶差分序列非白噪声序列。再对一阶差分序列进行ADF检验,显著性水平P=0.032 3<0.05,通过显著性检验,说明一阶差分序列具有平稳性。

通过以上检验,可知可以对一阶差分序列进行建模。

2.2.2 模型参数选择

计算一阶差分序列自相关(auto-correlation function,ACF)系数和偏相关(partial auto-correlation function,PACF)系数,自相关函数图和偏相关函数图如图4所示。

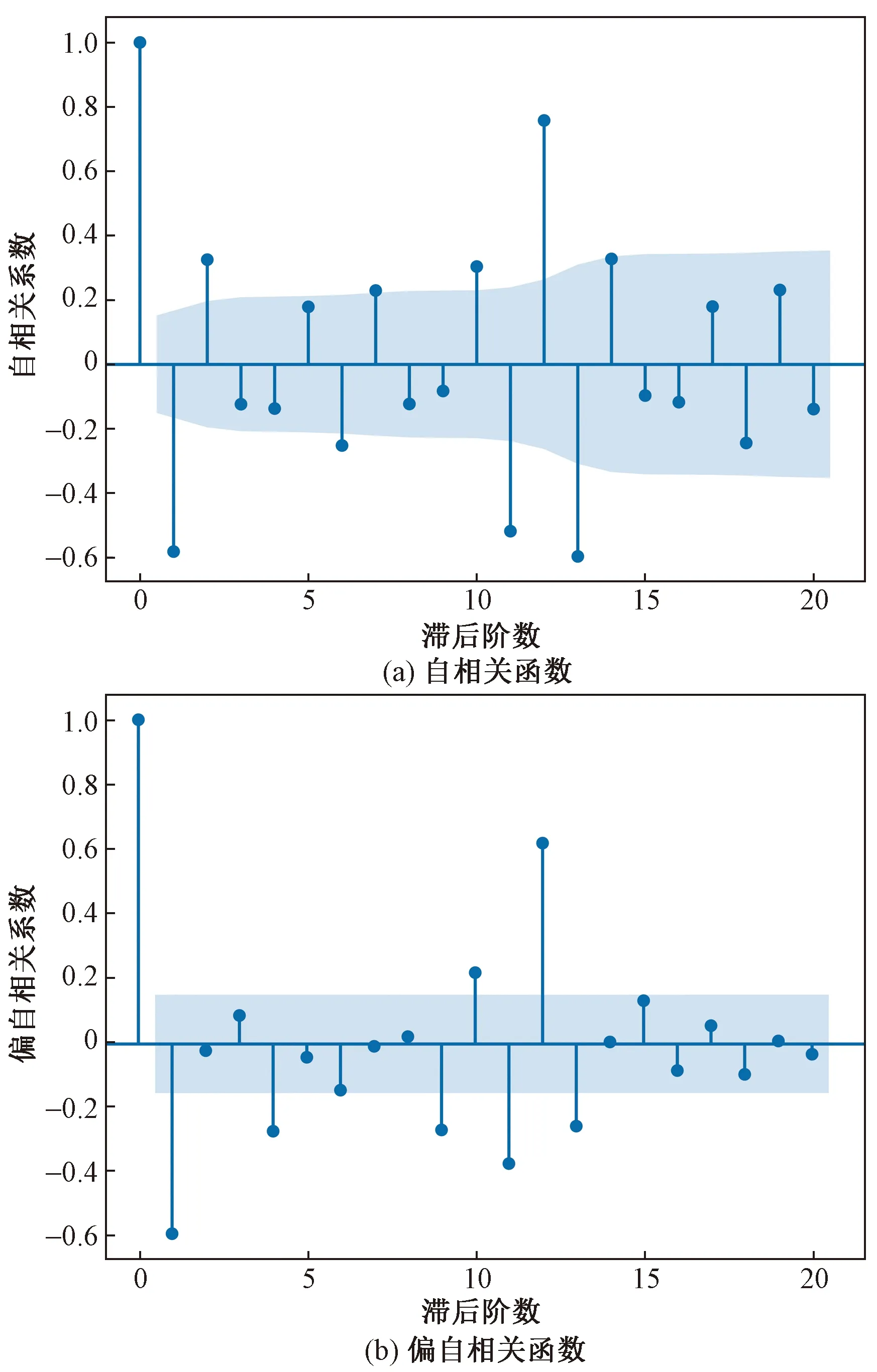
图4 自相关函数、偏自相关函数图Fig.4 Autocorrelation function, partial autocorrelation function diagram

由图4可知,ACF图和PACF图均表现出拖尾性,满足使用ARIMA算法的条件。

因为BIC准则比AIC准则拥有更大的惩罚因子,可避免过拟合现象,故采用BIC准则来确定参数p和q的值。

通过比较得出,ARIMA(4,1,3)的BIC值最小,说明该模型对数据的拟合效果最好。

2.2.3 模型检验

使用残差QQ图和残差正态分布直方图检验模型的适用性,残差检验结果如图5所示。可见散点分布在拟合线附近且残差满足正态分布,说明该序列通过正态性检验。

图5 模型残差检验图Fig.5 Model residual test diagram

再进行Durbin-Watson(D-W)检验,其检验值为2.5,说明残差序列中无明显的自相关性。对残差进行白噪声检验,检验统计量P>0.05,残差序列为白噪声序列,模型已经完全提取了原始时序数据中的线性特征,说明模型适用于序列的变化趋势。

2.2.4 模型预测

建立ARIMA(4,1,3)模型后,将数据集中前168个月(即2007年1月—2020年12月)的货运量数据作为训练数据,对后12个月的货运量进行预测,得到2021年1—12月月度货运量预测值。

2.3 ARIMA-LSTM模型建立

使用LSTM模型对ARIMA模型预测残差序列进行训练拟合以进行误差修正,模型建立过程如下。

步骤1数据预处理。将ARIMA模型预测的残差作为输入数据,使用最大最小法将其进行归一化以提高模型的训练效果。

步骤2训练模型。将残差序列中前168条数据作为训练集,后12条数据作为测试集,基于Python 3.6平台,采用Tensorflow框架搭建LSTM网络,通过实验,确定步长time_steps=12,即使用前12个月的货运量误差预测下个月货运量误差,采用单层隐藏层的LSTM网络,隐藏层神经元个数为8,学习率为0.01,模型迭代次数为600,训练批次batch_size=64。损失函数为均方误差函数MSE,模型优化算法采用Adam,激活函数采用tanh函数。

步骤3模型预测。将LSTM网络输出数据进行反归一化,得到残差预测值。

步骤4ARIMA-LSTM预测结果。将ARIMA模型预测值与LSTM网络残差预测值叠加,即可得到ARIMA-LSTM模型预测结果。

2.4 XGBoost模型建立

基于Python 3.6平台,使用XGBoost包中的XGBRegressor建立XGBoost模型,使用机器学习库scikit-learn中的网格搜索(GridSearchCV) 方法对模型参数进行调优。XGBoost预测模型参数如表1所示。

表1 XGBoost模型参数Table 1 XGBoost model parameters

2.5 实验结果分析

建立ARIMA-LSTM预测模型和XGBoost模型后,分别对2021年1—12月铁路货运量数据进行预测,得出两个模型的预测值和预测误差,再使用误差倒数法根据预测误差对两个模型的预测值进行加权组合,得出组合模型的预测值。

为验证组合模型的预测精度和有效性,将组合模型的预测值与ARIMA、ARIMA-LSTM、LSTM、XGBoost 4个模型的预测值以及实际值进行比较。各模型预测值与实际值对比如图6所示。各模型逐点误差对比图如图7所示。各个模型的评价指标MAE、RMSE、MAE、MAPE值如表2所示。

表2 各模型评价指标对比Table 2 Comparison of evaluation indexes of each model

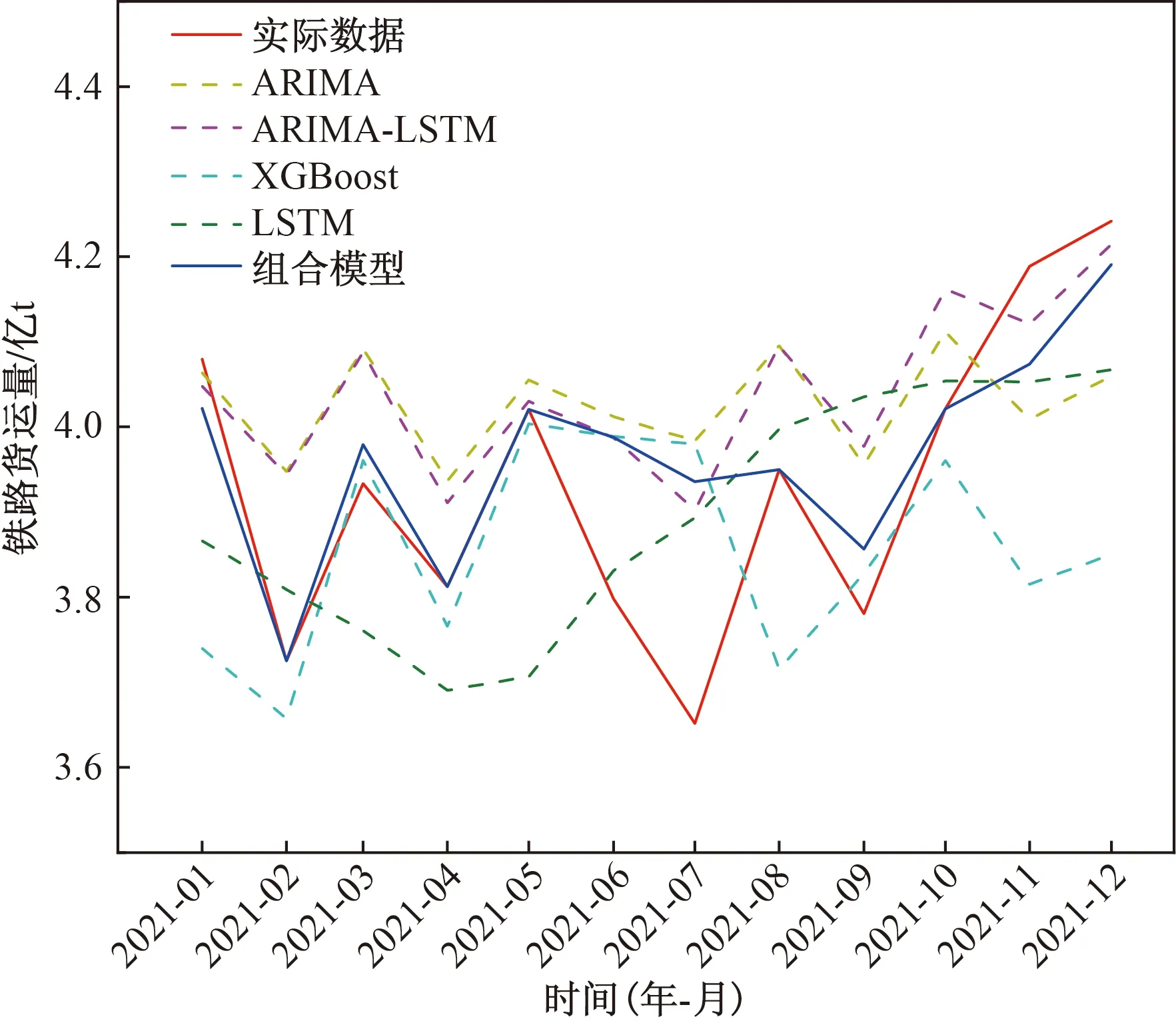
图6 各模型预测值与实际值对比图Fig.6 Comparison diagram of predicted value and actual value of each model

图7 各模型逐点误差对比图Fig.7 Comparison diagram of error point by point of each model

由图6和图7可知,以上大部分模型预测铁路货运量时预测误差比较小,有较高的精度。ARIMA模型预测结果与实际数据变化趋势大致相同,说明该模型较好地提取了序列中体现的线性特征。使用LSTM模型对ARIMA模型预测结果进行误差修正后,ARIMA-LSTM模型相对于单一的ARIMA模型和LSTM模型,预测精度得到了进一步的提升。XGBoost模型能较好地处理回归预测问题,整体上预测效果较好,但对个别数据的拟合效果欠佳。

ARIMA-LSTM-XGBoost组合模型能够充分结合3个模型的优点,弥补单一算法的不足,由图7可知,组合模型的预测误差同其他对比模型相比都有所降低。由表3可知,在对铁路货运量数据进行预测时,组合模型MSE、RMSE、MAE、MAPE分别为0.011 9、0.109 4、0.068 3、1.775 2%,均低于其他模型对应评价指标值,可见ARIMA-LSTM-XGBoost组合模型预测精度明显优于单一预测模型。以平均绝对百分比误差MAPE为例,相较于ARIMA、ARIMA-LSTM、XGBoost、LSTM模型,组合预测模型MAPE值分别降低了55.96%、 46.56%、60.03%、54.18%,可见组合模型的预测误差相比其他模型显著降低,预测精度和泛化能力得到有效提升。