基于风场实验的三维叠加尾流模型特性研究

张绍海, 高晓霞, 徐施耐, 朱霄珣, 王 瑜, 王 喜

(1．华北电力大学 动力工程系,河北保定 071003;2.河北省低碳高效发电技术重点实验室,河北保定 071003;3.保定市低碳高效发电技术重点实验室,河北保定 071003;4．华北电力大学 电子与通信工程系,河北保定 071000;5．河北龙源风力发电有限公司,河北张家口 076450)

近年来,常规化石燃料的消耗逐年增加,成本波动较大,对大气环境污染也日益严重,因此亟需研究和评估可再生替代能源。风能作为全球发电的重要来源,是重要的可持续能源[1-2]。尾流的存在会增加风力机的疲劳载荷,减小功率输出[3],尾流模型是研究尾流特征的重要手段。

解析尾流模型具有计算成本低、计算效率高等优点,因此被学者广泛研究。Jensen尾流模型[4]是典型的一维尾流模型,其假设风力机尾流只和下游位置有关,在水平以及垂直方向上的尾流均匀分布。风洞试验[5]和风场实验[6]都表明风力机下游的远尾流区水平剖面类似于高斯形状。基于此,Gao等[7]提出了一种二维Jensen-Gaussian尾流模型,认为风力机下游的尾流剖面为高斯形状,该尾流模型虽然能精确描述水平剖面的尾流分布,但忽略了风切变的影响,并不能描述垂直方向上的尾流速度变化特征。为了解决这一问题,随后Gao等[8]提出了一种考虑风切变的三维尾流模型,其能精确描述远尾流区的三维尾流分布特征,却忽略了近尾流的变化特征。最近,Gao等[9]提出了一种基于双高斯函数的三维全尾流模型(3DJGF模型),该模型能精确描述整个尾流区的三维分布特征,但其只能应用于单风力机尾流的预测,并不适用于叠加尾流。

然而,在实际风电场中风力机并不是单独存在的,所以学者们对叠加尾流进行了研究。Nakhchi等[10]通过大涡模拟分析了串列风力机的尾流变化特征。Shapiro等[11]提出一种以Jensen模型为基础的二维串列尾流模型,但是未考虑风切变的影响。刘智益等[12]提出了三维串列尾流模型,该尾流模型能很好地预测远尾流区的三维叠加尾流分布特征,但并未研究近尾流区的叠加尾流变化特征,而风电场中的风力机之间距离可能低于4倍风力机直径[13]。因此,叠加尾流模型应该准确预测远尾流以及近尾流区域的尾流分布特征。

笔者修正了3DJGF模型的尾流膨胀系数,并在速度亏损叠加原理中增加了风切变的影响,提出了一个新的叠加尾流模型(3DJGF-M模型),该模型能预测整个尾流区的叠加尾流速度,包括近尾流区和远尾流区。同时进行了风场实验,利用激光雷达获得了准确有效的现场实验数据,验证了3DJGF-M模型的有效性。

1 3DJGF-M模型的推导

1.1 三维坐标系

推导3DJGF-M模型,首先需要建立多风力机三维坐标系,如图1所示。以第1台风力机(未受尾流干扰的风力机)的轮毂中心为坐标原点,尾流流动方向(流向)为x轴,水平方向为y轴,垂直方向为z轴。设第i台风力机(Wi)轮毂中心的坐标为(xi,yi,zi)。

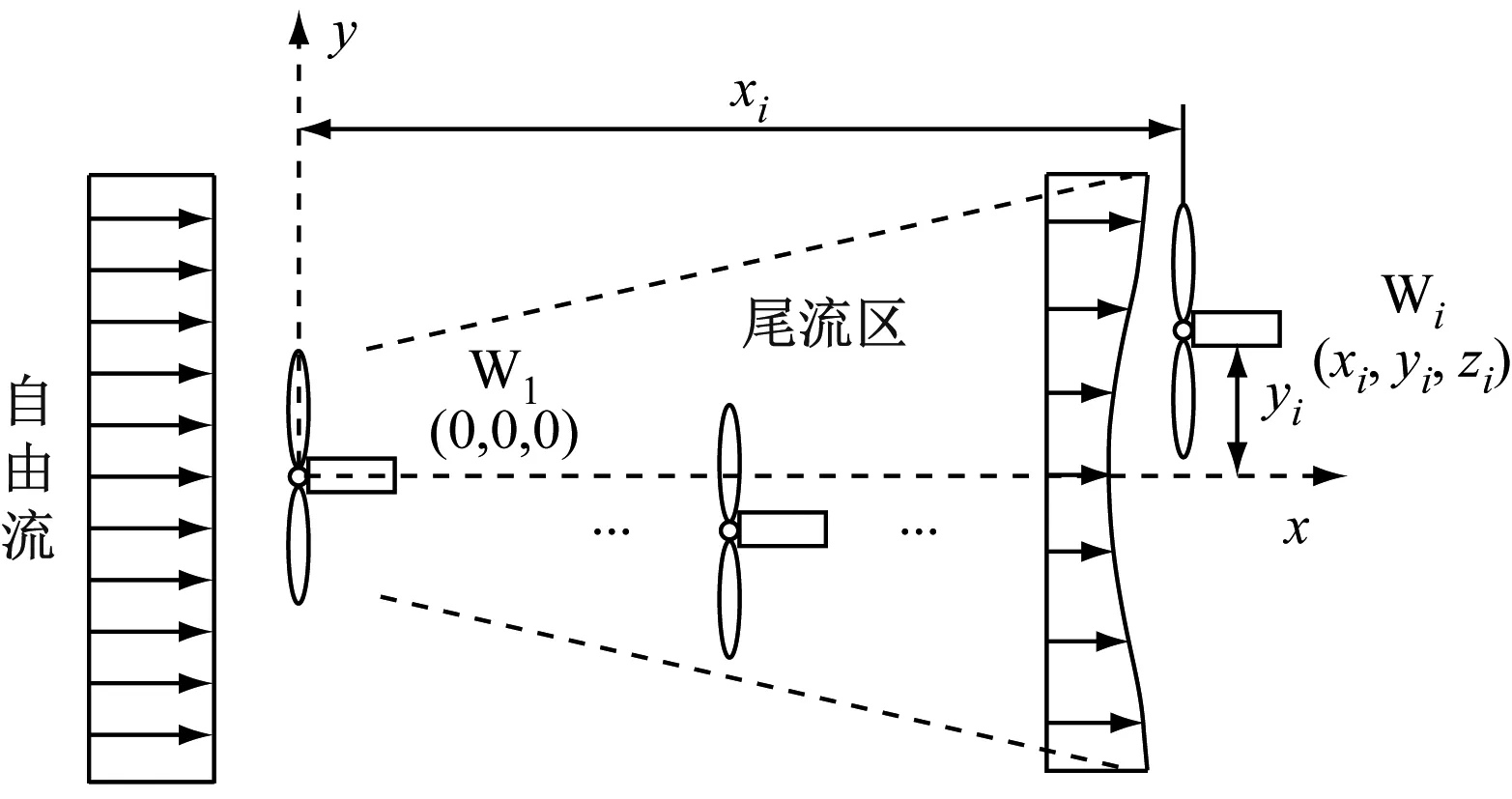
(a) 俯视图

1.2 风切变模型

在实际风场中,风速随着高度增加而逐渐增大,在垂直方向上的风速分布类似于指数函数。因此,采用式(1)所示的风切变模型[14]:

(1)

式中:u(z)为风切变自由流速度;uhub为第一台风力机轮毂高度处的来流风速;zhub为轮毂高度;α为风切变指数。需要注意的是,式(1)是以轮毂中心为坐标原点,其绝对高度对应为z+zhub。

1.3 3DJGF模型

Gao等[9]提出的3DJGF模型能够描述单风力机整个尾流区域的三维变化特征,因此笔者采用3DJGF模型作为推导叠加尾流模型的基础,其表达式如下:

(2)

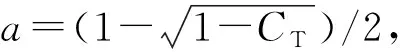
1.4 尾流膨胀系数的修正

3DJGF模型中的尾流膨胀系数表达式如下:

(3)

式中:I0为来流湍流强度。

从式(2)可以看出,3DJGF模型采用的尾流膨胀系数在入流条件不变的情况下为常数。事实上,尾流膨胀系数与风力机的下游距离有关[15],因此采用Gao等[7]提出的尾流膨胀系数表达式来修正3DJGF模型:

(4)

式中:kr为修正后的尾流膨胀系数;k为Jensen尾流膨胀系数,在陆上风电场为0.075,海上风电场为0.04[4];Iw为尾流湍流强度;kn为经验参数,kn=0.04[8,15]。

结合式(4)和式(2)可得修正后的3DJGF模型。

1.5 速度亏损叠加模型的改进

Lissaman[16]提出了一个基于速度差线性叠加的累积速度差模型。该模型将风力机在大气边界层中的尾流膨胀和点源污染物分散进行类比,得到的速度亏损叠加模型如下:

(5)

式中:uN为叠加尾流速度。

Lissaman叠加模型并未考虑风切变的影响,所以该模型并不能描述垂直方向上的尾流变化特征。笔者结合式(1)和式(5),提出了一个考虑风切变的尾流叠加模型:

(6)

其中,ui(x,y,z)由修正后的3DJGF模型计算得到。

2 风场实验

实验风电场位于中国北方的河北省张家口市。由于处于不同的施工阶段,该风电场中有3种类型的风力机。其规格参数如表1所示。

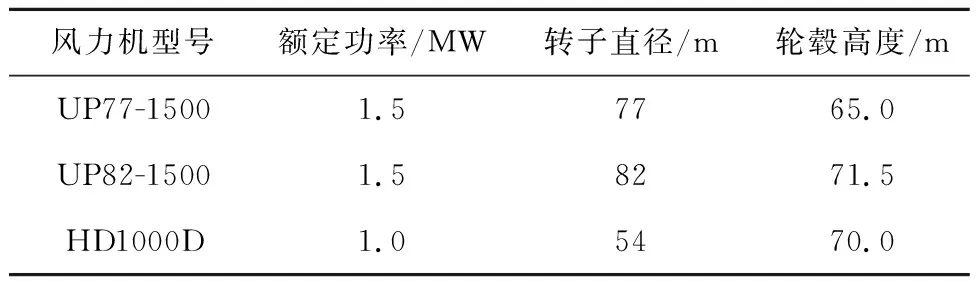
表1 风力机的特征参数

为了深入研究复杂的尾流相互作用,本实验采用2台Wind3D6000激光雷达扫描尾流区域,1台WP350激光雷达测量来流风速信息。激光雷达的具体参数见表2。

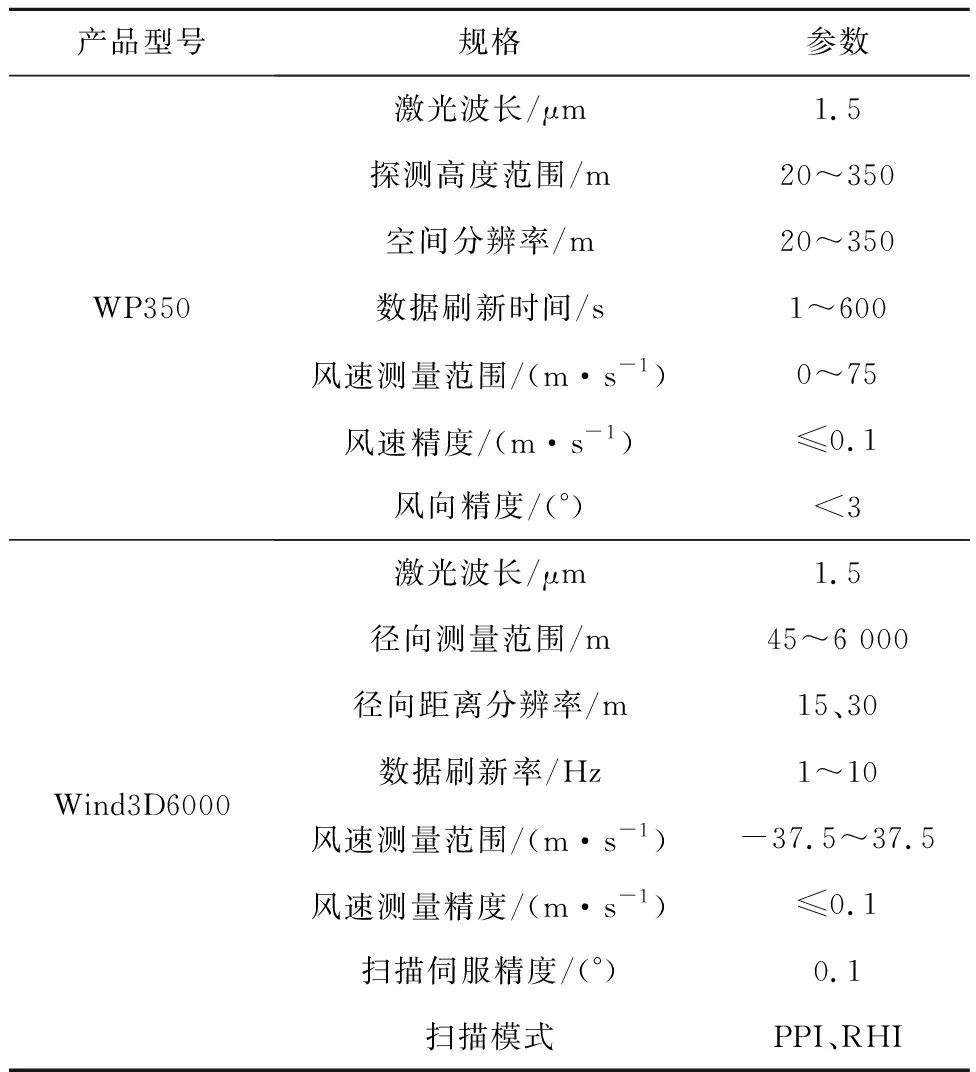
表2 激光雷达技术指标

在所研究的尾流相互作用区域内有2种类型的风力机(HD1000D和UP77-1500)。这2种风力机的推力系数曲线如图2所示。

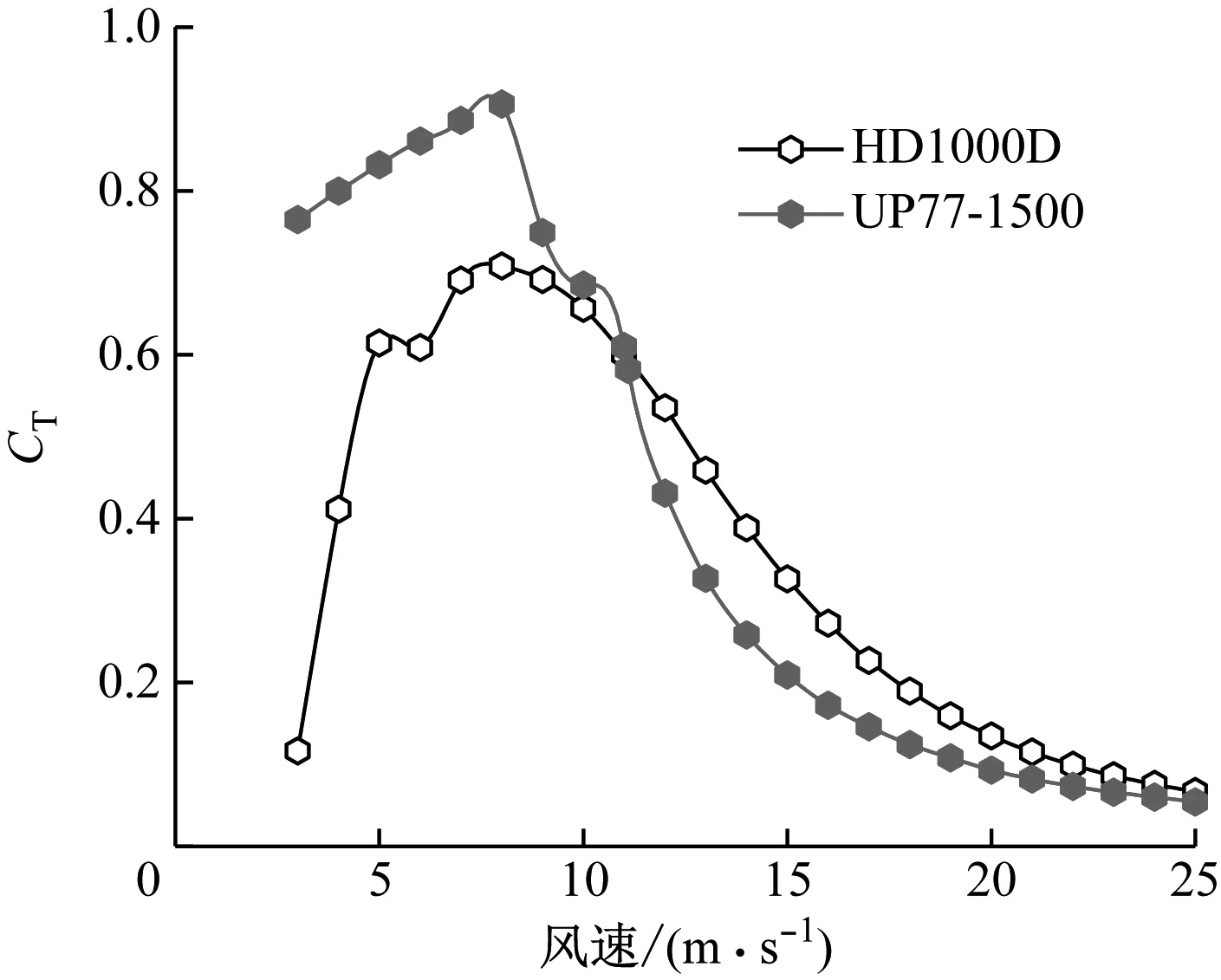
图2 推力系数曲线

图3的实线方框内为UP77-1500型号风力机区域,点划线方框内为HD1000D型号风力机区域。1号激光雷达用来扫描HD1000D型号风力机,2号激光雷达用来扫描UP77-1500型号风力机,如图3所示。

图3 实验仪器布置

3 结果与分析

3.1 尾流中心线(y=0,z=0)的验证

图4为2号激光雷达在2019年5月25日测量的水平剖面尾流速度云图,该图以2号激光雷达为坐标原点,横轴为纬度方向,纵轴为经度方向。从图4可以看出,风力机UP-3(UP77-1500型号)的尾流完整且处于上游风力机UP-2(UP77-1500型号)的全尾流下,因此将UP-3作为验证3DJGF-M模型的目标风力机。由风电场提供的风力机坐标信息可知,UP-2与UP-3相距约462 m(6D),UP-2和UP-3的海拔高度都为1 550 m,则以UP-2的轮毂中心为坐标原点,UP-3的轮毂中心坐标为(6D,0,0)。

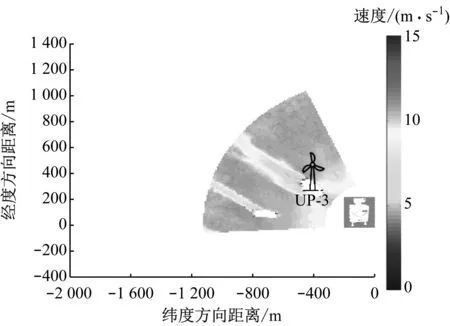
图4 水平剖面(z=0平面)尾流速度云图

由WP350激光雷达测量的UP-2来流风速uhub=10.2 m/s,由图2可得对应的推力系数CT=0.68,10 min内的平均来流湍流强度I0=0.12。

图5给出了3DJGF-M模型预测的尾流中心线和实验数据的对比结果。图5(a)为尾流中心线的预测曲线和实测数据比较结果,横轴为下游距离和风力机直径的无量纲比,纵轴为尾流速度和第一台风力机轮毂中心处来流风速的无量纲比;图5(b)为3DJGF-M模型预测值和实验数据之间的相对误差。

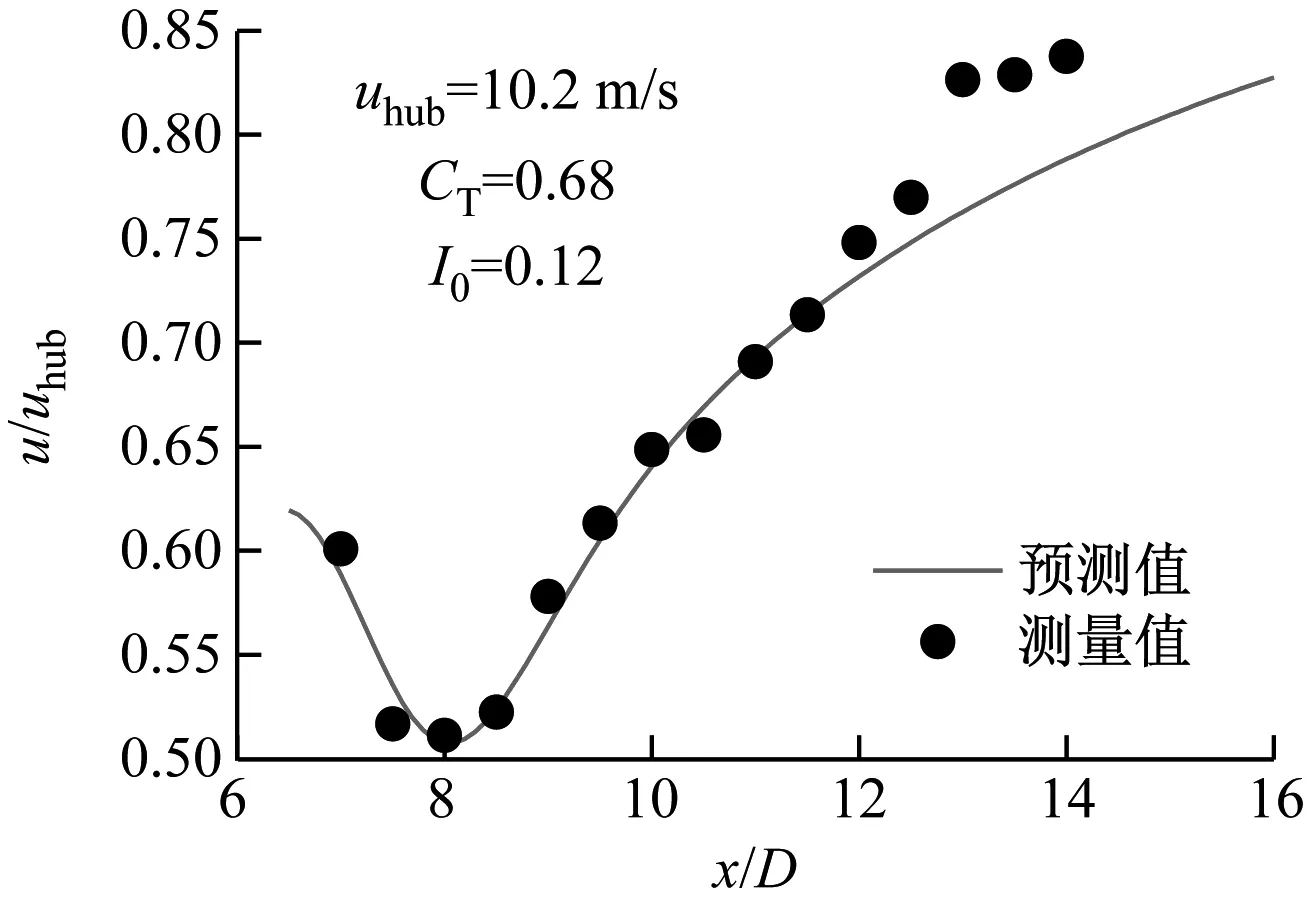
(a) 尾流中心线的尾流速度预测

由实验数据可以看出,尾流中心线上的尾流速度先减小后增大,在x=8D左右达到最小值,这与3DJGF-M模型预测结果一致。值得注意的是,当x>12.5D时,3DJGF-M模型预测精度较差,最大误差在x=13D处,达到7.7%。这可能是因为在较远的尾流区还存在其他风力机的尾流干扰,导致3DJGF-M模型计算的尾流风速要比实际的尾流风速低。而其他位置的相对误差都在4%以内,说明3DJGF-M模型能够较好地预测尾流中心线上的速度。

3.2 水平剖面(z=0平面)的验证

为了体现3DJGF-M模型在预测整个尾流区域水平剖面的准确性,对UP-3风力机下游的8个位置的水平剖面尾流速度进行对比验证,包括近尾流区域以及远尾流区域,如图6所示。由图6可以看出,随着下游距离的增加,尾流的水平剖面由近尾流区域的双高斯形逐渐过渡为远尾流区的高斯形,这和3DJGF-M模型的预测结果一致。

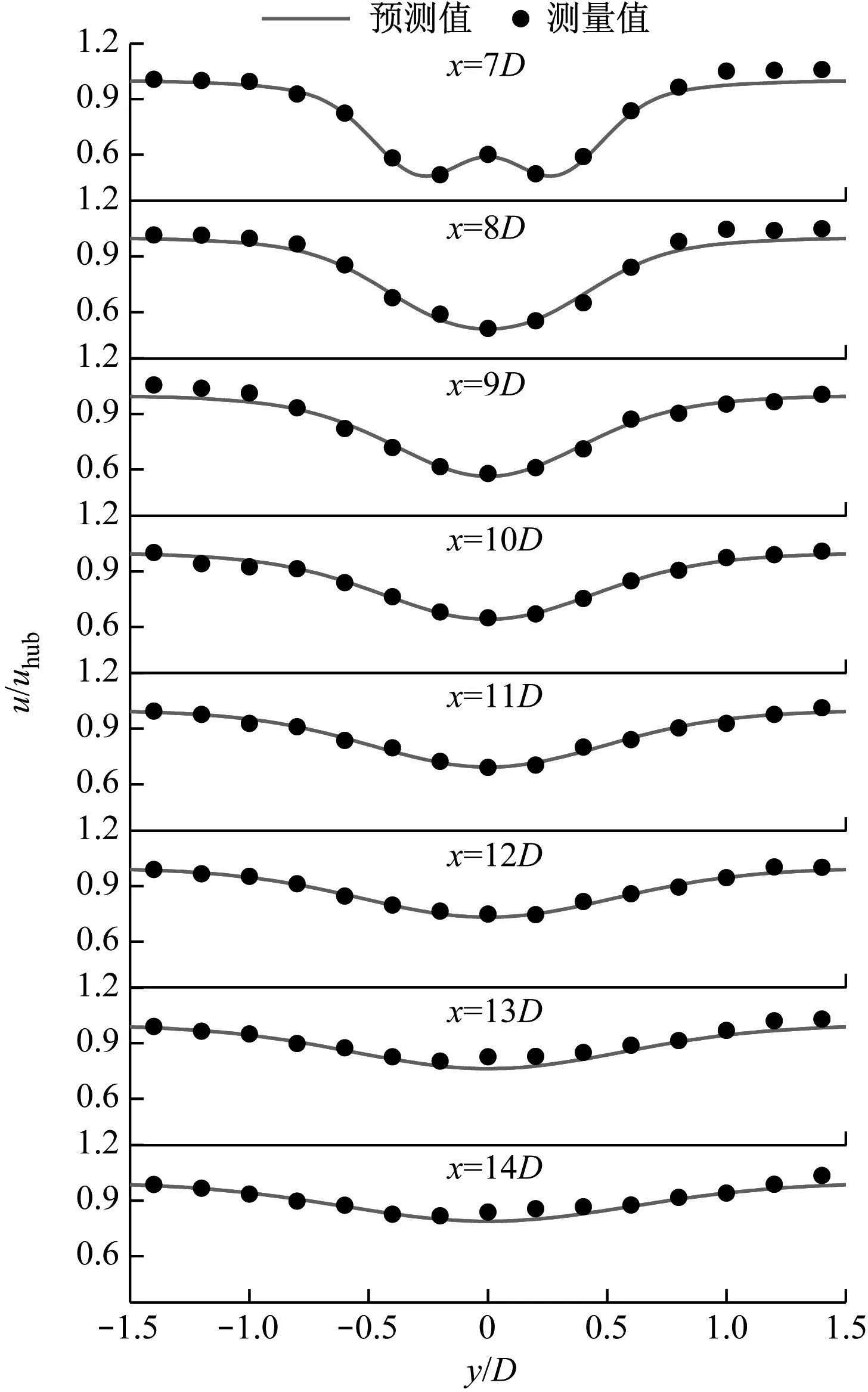
图6 下游8个位置的水平剖面(z=0平面)尾流速度预测

为进一步分析模型预测精度,计算了3DJGF-M模型对下游8个位置的水平剖面尾流速度预测的相对误差,如图7所示。

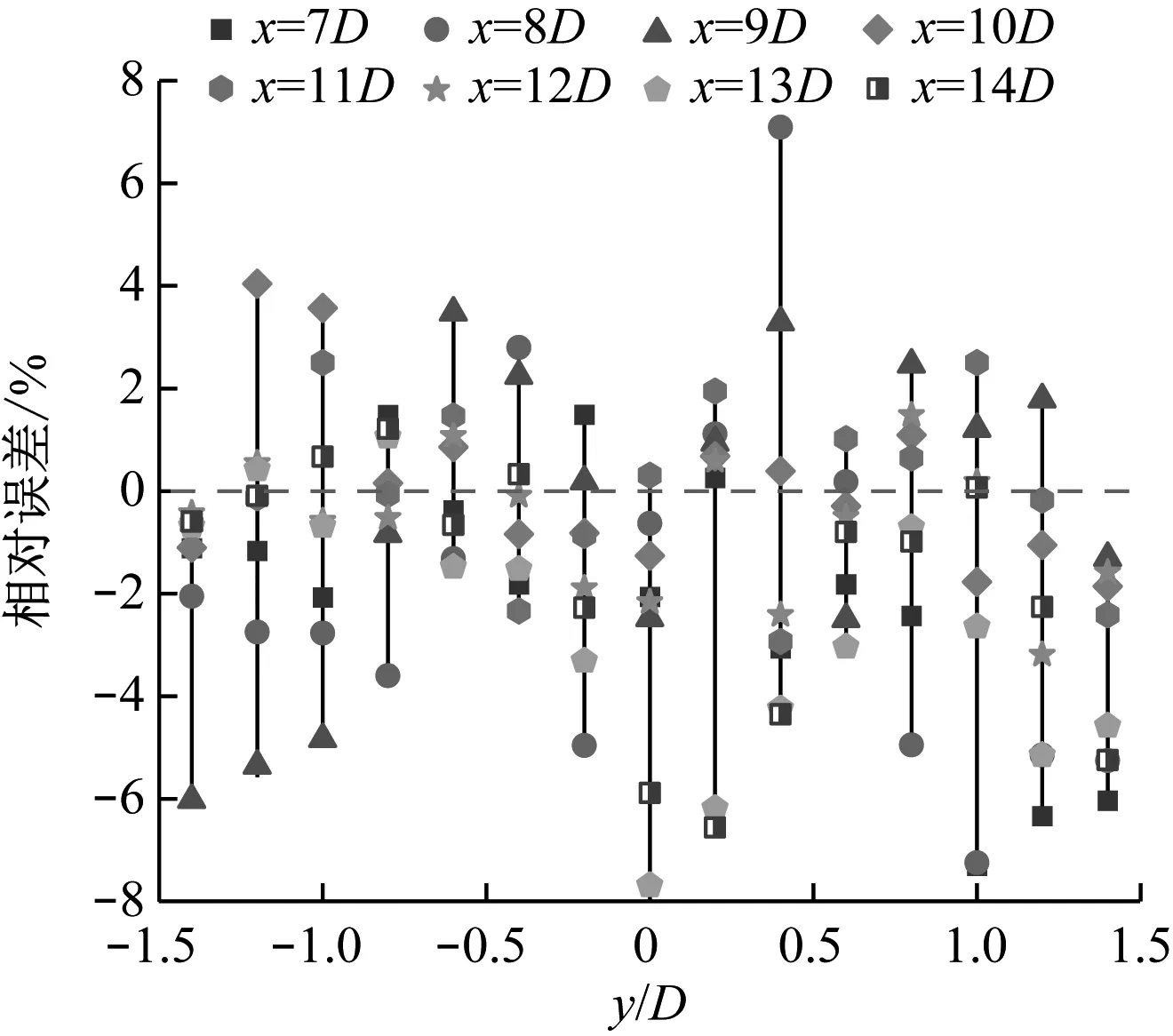
图7 下游8个位置的水平剖面尾流速度相对误差

从图7可以看出,3DJGF-M模型的相对误差基本都在5%以内,最大相对误差在下游x=13D的y=0处,为7.7%,这和尾流中心线分布相对应。由于实验仪器本身存在一定的测量误差,再加上实验现场风况复杂多变,导致实验测量值和实际值存在一定的差异,因此3DJGF-M模型预测值和实验值之间存在7.7%的最大相对误差是可接受的。以上分析表明,不管近尾流区还是远尾流区,3DJGF-M模型都能较好地预测尾流的水平剖面分布。

3.3 垂直剖面(y=0平面)的验证

本次实验测量了单风力机在垂直方向上的尾流分布,但并未测量多风力机尾流的垂直剖面数据。因此,选取单风力机垂直剖面尾流速度来验证3DJGF-M模型在垂直方向上的预测准确性。

图8给出了Wind3D6000激光雷达在2019年1月6日测量的风力机UP10-2(UP77-1500型号)垂直剖面尾流速度云图,该图以激光雷达为坐标原点,水平轴为经度方向,垂直轴为垂直方向。

图8 垂直剖面(y=0平面)尾流速度云图

由WP350激光雷达测量的UP10-2来流风速uhub=9.2 m/s,由图2可得对应的推力系数CT=0.72,10 min内的平均来流湍流强度I0=0.11,拟合的风切变指数α=0.14。

图9为3DJGF-M模型在下游4个位置(包括近尾流区和远尾流区)的尾流速度预测结果。可以看出,由于垂直剖面存在风切变的影响,所以尾流的垂直剖面总体上呈现非对称分布。随着下游距离的增加,尾流的垂直剖面由近尾流区域的非对称双高斯形逐渐过渡为远尾流区的非对称高斯形,这与3DJGF-M模型的预测值吻合。

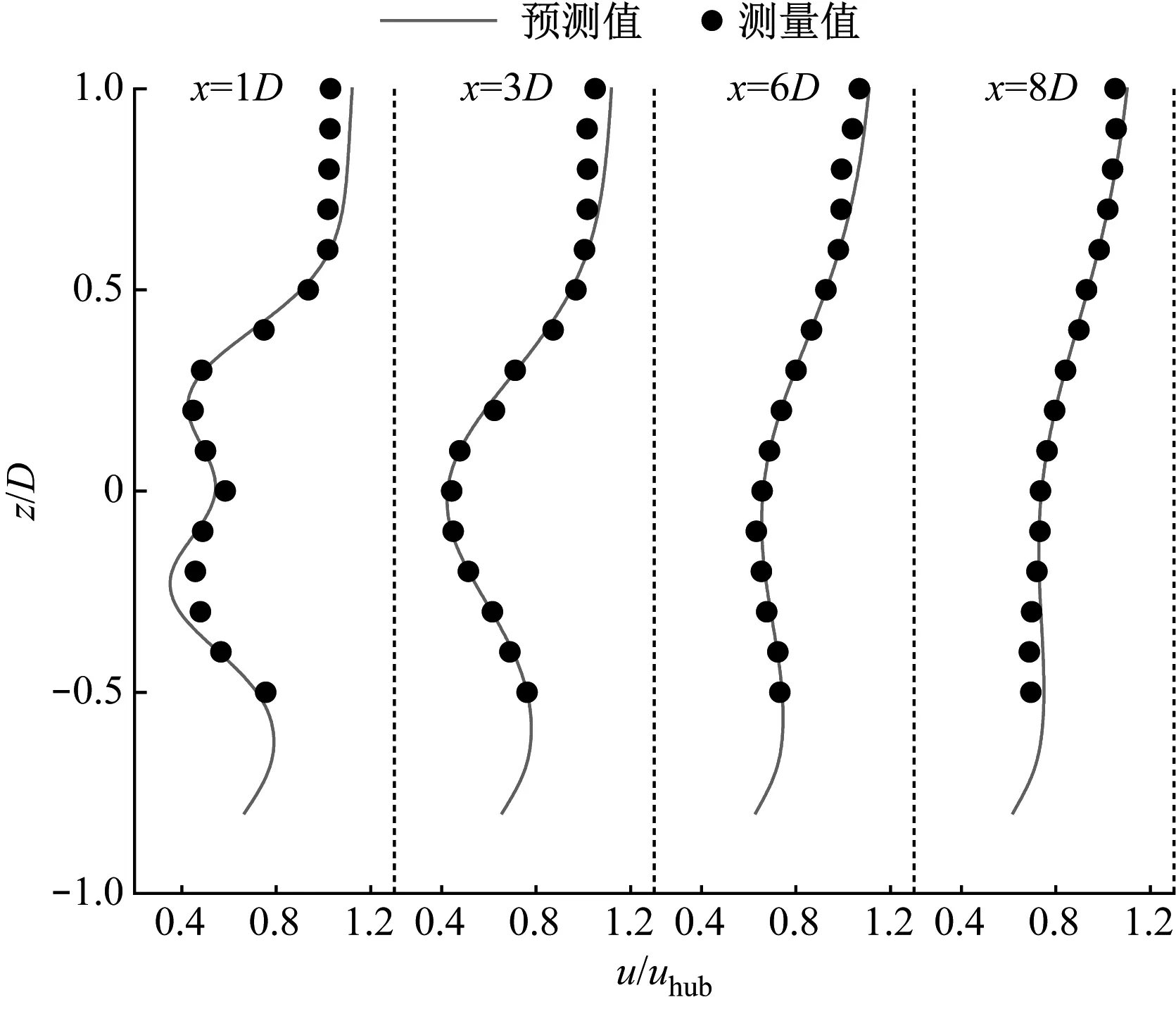
图9 下游4个位置的垂直剖面(y=0平面)尾流速度预测

为了进一步对3DJGF-M模型预测精度进行分析,图10给出了3DJGF-M模型预测的垂直剖面尾流速度的相对误差。从图10可以看出,3DJGF-M模型的预测误差基本都在5%以内,其整体预测效果良好。值得注意的是,尾流模型明显低估了下半尾流区的尾流速度,其最大相对误差达到28%,出现在下游x=1D的z=-0.2D处。这可能是由于实际风场中,地面环境复杂,可能存在陡坡或者植被,增加了下半尾流区尾流湍流变化的复杂程度,从而导致尾流模型在下半尾流区的预测精度较差。

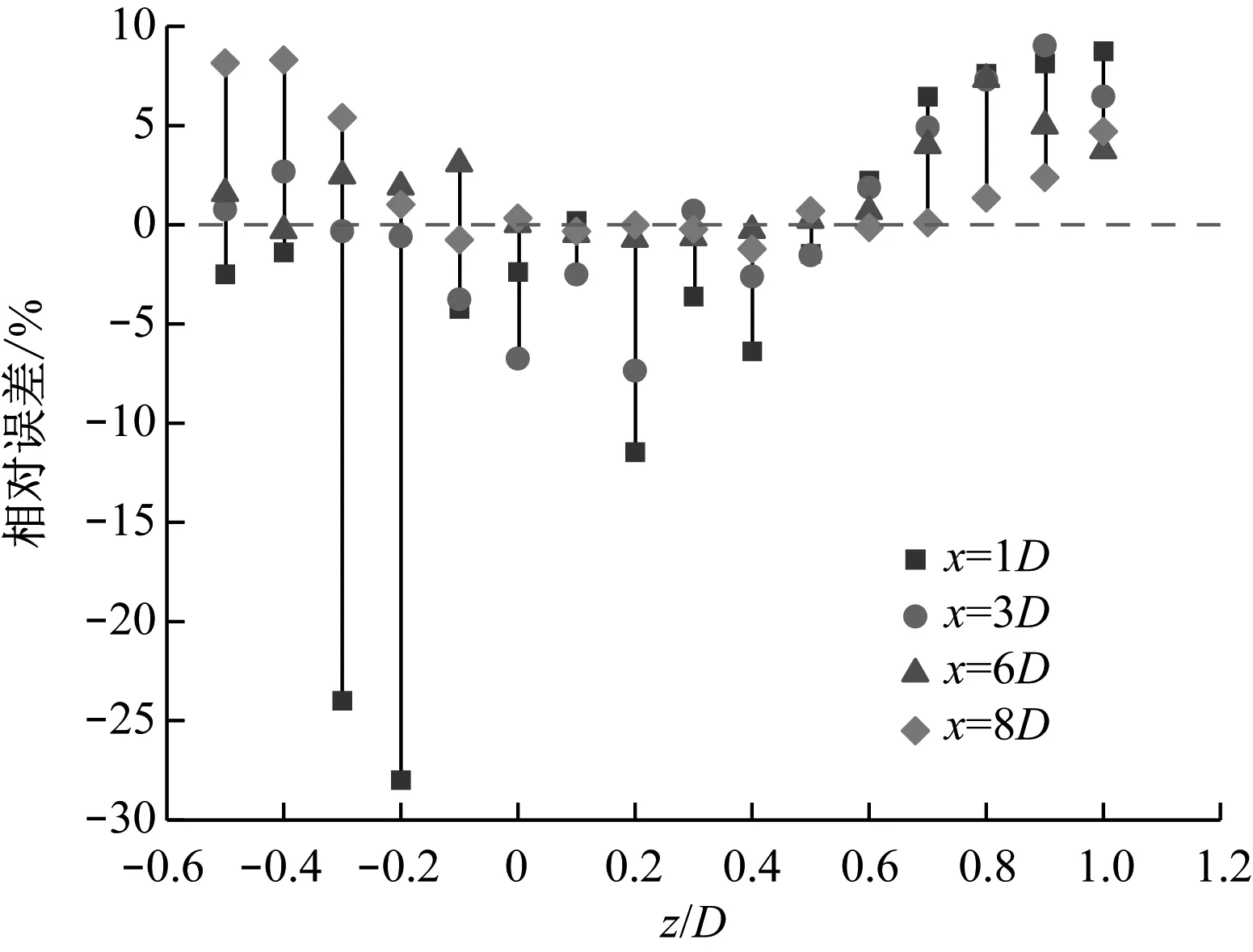
图10 下游4个位置的垂直剖面尾流速度相对误差

4 结 论

(1) 与以往的叠加尾流模型相比,该模型有以下改进:采用了和下游距离相关的尾流膨胀系数,使尾流模型的预测结果更准确,且不需要复杂的实验计算来确定经验参数,节约了计算成本;在尾流叠加原理中引入了风切变的影响,使3DJGF-M模型能够预测垂直剖面的尾流速度分布;3DJGF-M模型能够描述整个尾流区的变化特征,由近尾流的双高斯形(非对称双高斯形)平滑过渡到远尾流区的高斯形(非对称高斯形)。

(2) 利用2台Wind3D6000激光雷达和1台WP350激光雷达捕捉尾流的空间分布信息和来流风速信息。从捕捉到的尾流数据可以看出,多风力机的尾流中心线上的速度先减小后增大,在x=8D左右达到最小值;近尾流区的水平剖面分布类似于双高斯分布,远尾流区的水平剖面类似于高斯分布;由于风切变的影响,近尾流区的垂直剖面分布类似于非对称双高斯分布,远尾流区的水平剖面类似于非对称高斯分布。

(3) 将3DJGF-M模型的预测值和实验值进行比较,并进行了相对误差分析,3DJGF-M模型在预测尾流中心线、水平剖面以及垂直剖面尾流速度的相对误差基本都在5%以内。结果表明,3DJGF-M模型能够较好地预测整个尾流区的尾流中心线、水平剖面以及垂直剖面的尾流速度分布。

(4) 所提出的3DJGF-M模型可为风电场的布局优化提供参考,减少尾流的影响,提高风电场收益。由于实验条件的限制,并未测量到叠加尾流的垂直剖面分布,在以后的工作中将进行叠加尾流垂直剖面数据的测量,完善模型的验证。