超大型近海风力机海流冲刷下的动力学响应分析
2023-09-26师浩东闫阳天牛凯伦
师浩东, 闫阳天, 马 璐, 李 春,3, 牛凯伦
(1.上海理工大学 能源与动力工程学院,上海 200093; 2.中国长江三峡集团有限公司,武汉 430010; 3.上海市动力工程多相流动与传热重点实验室,上海 200093)
随着能源短缺问题的日渐严峻,可再生能源得到重视[1]。在可再生能源领域,风能因技术相对成熟、污染较小等优点得到广泛关注,被认为是最有前景的能源之一[2]。我国陆地辽阔,海岸线长,气象局组织的陆海风能资源评估结果显示,海上风能资源总量约为600 GW,这为海上风能的开发奠定了坚实基础[3]。
我国陆地风能资源多集中于北方地区,但人口居住密度较高、用电量较大的地区为东南沿海地区,长距离输电给电网带来很大挑战[4]。我国沿海地区海上风能资源丰富,距电力负载中心近,风向稳定,风能密度大,湍流较小,较陆上风能,海上风能发展潜力更大[5-6]。
与陆地环境相比,海上及潮间带环境更加复杂多变,风力机基础会受到风载荷和波浪载荷等环境载荷影响,进而形成较大的横向(垂直风向方向)载荷,这对风力机的正常运行带来巨大挑战[7]。在海洋环境中,桩基的存在会改变水流流态,进而导致桩基附近出现局部冲刷现象。风力机遭到破坏的因素很多,其中桩周冲刷是一个重要原因[8]。在形成冲刷后,桩基的埋土深度大幅度减小,导致剩余土壤的结构应力改变,风力机自振频率也随之变化,而自振频率偏移可能会导致风力机发生共振,造成严重损失[9]。
学者对单桩基础冲刷进行了大量研究。胡丹等[10]通过实验和数值计算分析了桥墩冲刷前后桩基水平方向极限承载力的变化规律,发现随着冲刷深度的增加,桥墩水平极限承载力缓慢下降,但该研究未考虑风载荷和波浪载荷。王兆耀等[11]通过实验以及对波浪水槽进行数值计算,验证了大直径单桩局部冲刷的特征,结果表明局部冲刷发展主要分为纵向切蚀、横向扩展和基本稳定3个阶段。黎蔚杰等[12]采用数值计算方法,通过求解重整化群(Renor-malization Group,RNG)k-ε湍流模型封闭的N-S方程,来模拟桩周流场变化,研究波流联合作用和各自单独作用下单桩周围海床的局部冲刷。陈静等[13]对5 MW单桩式海上风力机进行研究,发现随着冲刷深度的增加,单桩基础泥面处最大倾覆力矩也会增大,一阶自振频率降低,这与文献[14]中的研究结果一致。Sørensen等[7]研究发现在单桩形成局部冲刷时,一般情况下波浪形成的冲刷坑深度相对较小,而洋流形成的冲刷坑深度相对较大。刘红军等[15]采用黄河粉土数据建立桩-土耦合效应模型,并基于此,在风浪载荷下对风力机进行模态及瞬态动力学分析。
在上述关于单桩基础冲刷的研究中,大多仅集中在冲刷机制和过程,有关风力机在风浪作用下的冲刷动力学响应研究较少,而冲刷所造成的特性变化更值得关注。笔者以10 MW风力机为研究对象,通过建立土-构耦合模型及壳单元模型,对比不同桩周冲刷深度下风力机自振频率和瞬态动力学响应。
1 研究对象
1.1 海上单桩冲刷机理
常见的海上风力机基础结构主要分为单桩式、重力基础、三脚架、筒形和浮动基础5类[16],在水深小于25 m的浅水区首选单桩式基础[17]。在海洋环境中,风力机单桩式基础会改变水流流动模式,使桩基附近水流流速加快,桩基前形成马蹄形漩涡,桩后背风有尾流产生,波浪发生破碎并形成强烈的湍流,导致形成局部冲刷。此外,如果波浪载荷过大,将会在海床附近形成大规模冲刷,形成整体冲刷[18]。图1为单桩周围水流流态。图2为单桩局部冲刷原理示意图。
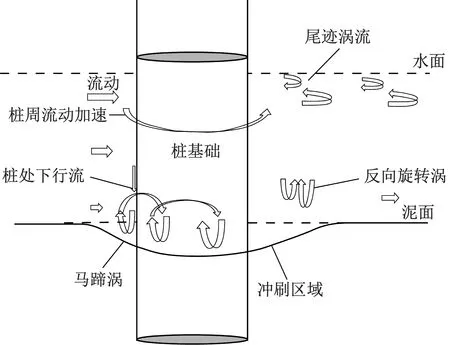
图1 单桩周围水流流态
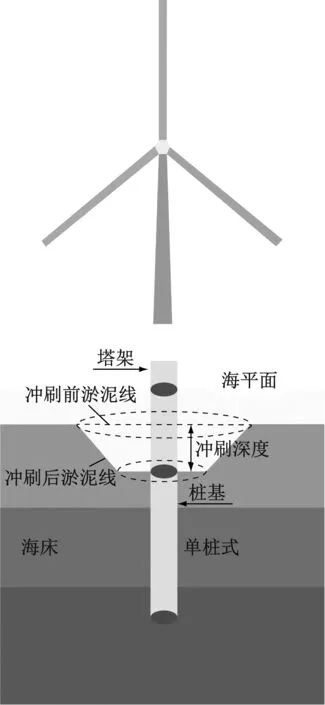
图2 单桩局部冲刷原理图
为研究单桩冲刷机理,Sumer等[19]对冲刷深度进行了大量研究,得出冲刷深度与库尔根-卡本脱数(Keulegan-Carpenter,KC)之间的关系。KC表征桩周波浪冲刷强度,KC越大,马蹄形漩涡越剧烈。根据挪威船级社(DNV)[20]推荐,管状单桩周围平衡冲刷深度为:
(1)
式中:S为冲刷深度,m;D为桩基直径,m。
目前,关于海上单桩式风力机的设计规范,DNV建议最大冲刷深度应为桩直径的1.3倍。因海洋环境存在诸多不稳定因素,笔者研究了不同冲刷深度下风力机的动力学响应,冲刷深度分别取为0 m(未冲刷)、0.32D、0.64D、0.96D和1.28D。
1.2 海上单桩风力机模型
以10 MW单桩式近海风力机为研究对象,主要参数如表1所示[21]。
塔架材料采用Q345结构钢,塔架壁厚随高度的增加线性减小,塔基外径为9.5 m,壁厚为0.150 m,塔顶与机舱连接处外径为5.5 m,壁厚为0.026 m,轮毂高度为119 m,将轮毂和叶片质量简化为塔顶质量点。图3为风力机模型简化图。
风力机模型材料的主要参数如表2所示。
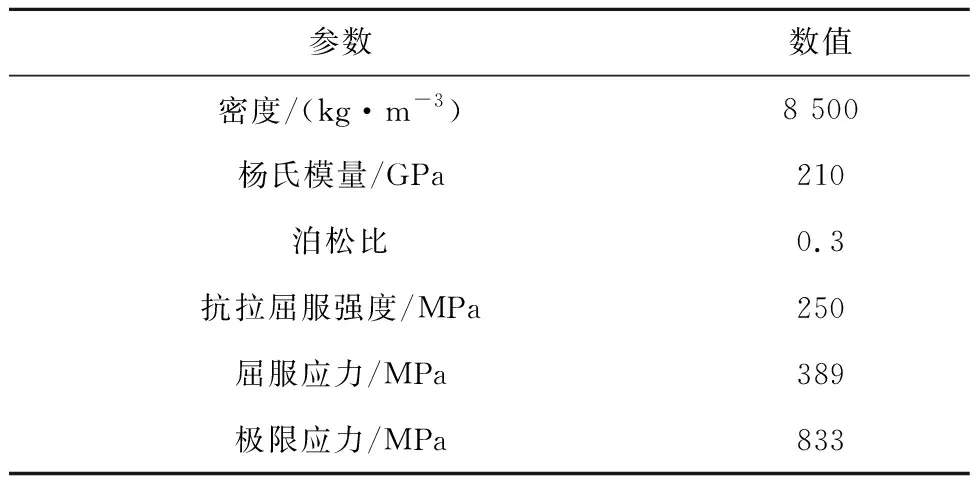
表2 风力机模型材料主要参数
ANSYS中常设置的阻尼可分为Alpha阻尼、Beta阻尼、模态振型阻尼、材料阻尼、单元阻尼及恒定阻尼比。其中Alpha阻尼、Beta阻尼合称为瑞利阻尼,在动力学计算中常用这种阻尼以反映结构阻尼,瑞利阻尼被广泛应用于各种工程问题并可满足计算要求,已成为工程中最常用的阻尼形式[22]。Alpha阻尼φ及Beta阻尼系数η由式(2)和式(3)确定[23]。
φ=2ζab·(a+b)-1
(2)
η=2ζ·(a+b)-1
(3)
式中:ζ为阻尼比,ζ=1%;a、b为整机自振频率,a=0.2 Hz,b=0.21 Hz;φ为0.02;η为0.05。
基于10 MW单桩式风力机参数,建立壳单元模型,为保证足够的计算精度,提高计算效率,将塔架模型网格划分为2部分。入水段以上为未加密区,网格尺寸取0.8 m,入水段以下为加密区,网格尺寸取0.6 m。图4为风力机模型网格分布图。
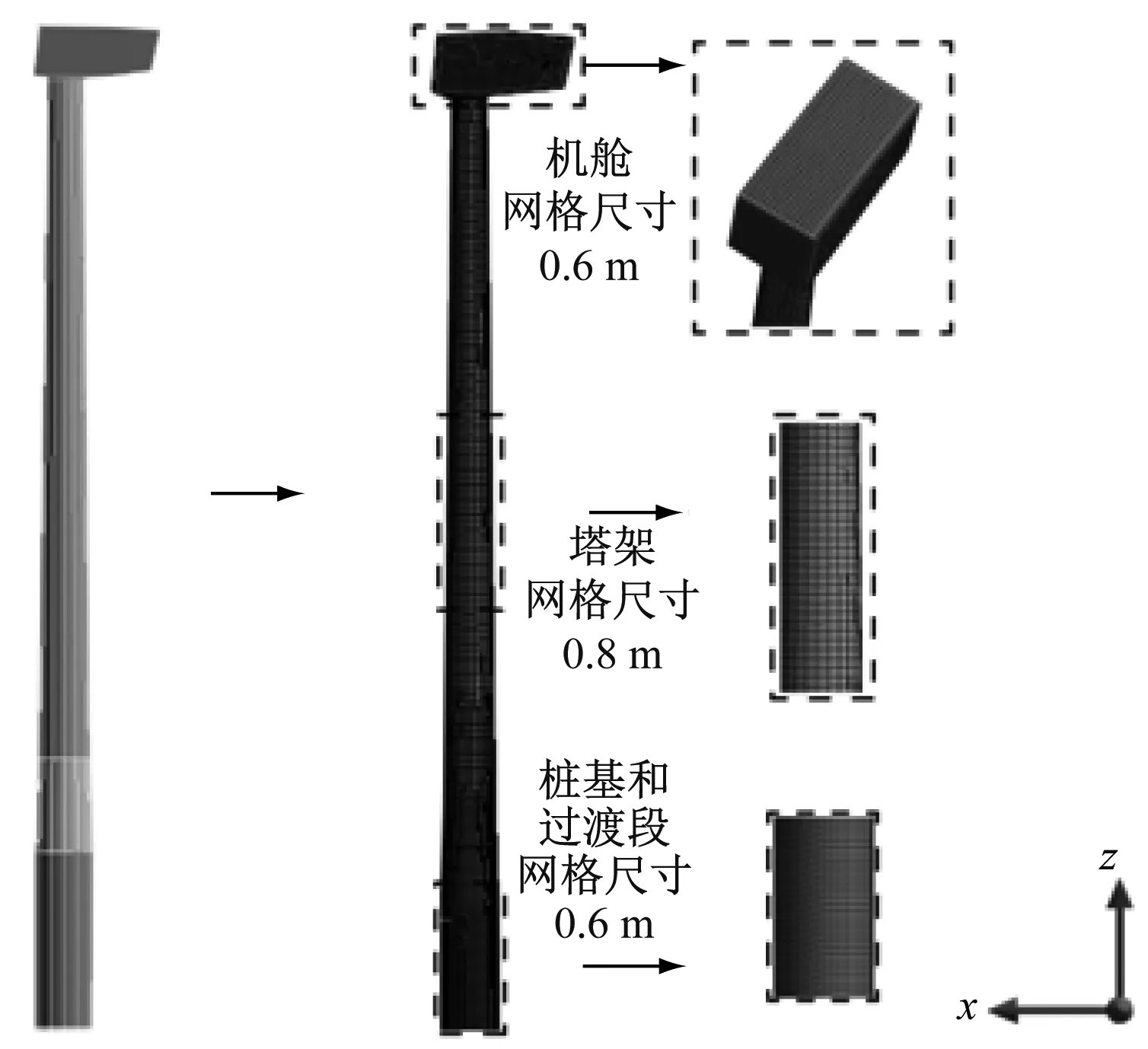
图4 单桩式风力机模型网格分布
1.3 土-构耦合模型
在海洋环境中,受到风浪载荷激励后风力机桩基会发生形变,土体为阻止其形变与桩基产生的相互作用力称为土-构耦合效应[24]。在海洋工业中通常采用分布式弹簧模型,此模型将土壤桩基相互作用表示为一系列非线性弹簧[25],如图5所示。
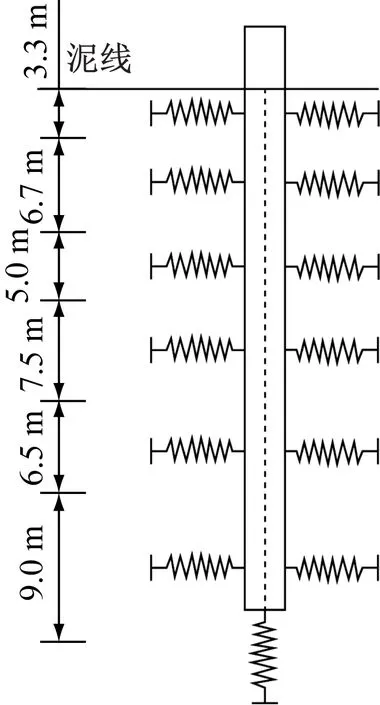
图5 土-构耦合模型原理图
在海洋环境中,不同深度土壤性质有所不同。不同深度的土壤参数如表3所示。
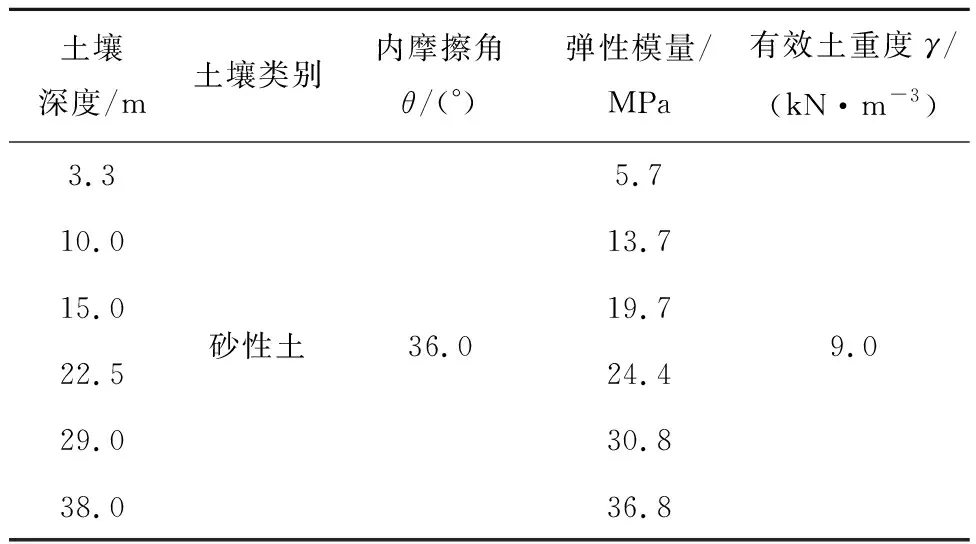
表3 土壤参数
风力机受环境载荷后,塔架横向位移会导致桩与土壤之间的作用力呈非线性变化,对于砂性土,不同深度下土壤与桩基之间水平承载力不同[26]。
p=ξputanh[kHy/(ξpu)]
(4)
pu=min{pus,pud}
(5)
pus=(C1H+C2D)γH
(6)
pud=C3DγH
(7)
ξ=(3-0.8H/D)
(8)
式中:ξ为经验调整系数;H为土壤深度;p为土壤反力;y为横向位移;pu为极限承载力;k为地基反力系数;C1、C2和C3均为系数,由内摩擦角φ确定,其值分别为3.2、3.6及60;下标us表示土壤较浅,ud表示土壤较深。
图6为不同深度下土壤的p-y曲线图。
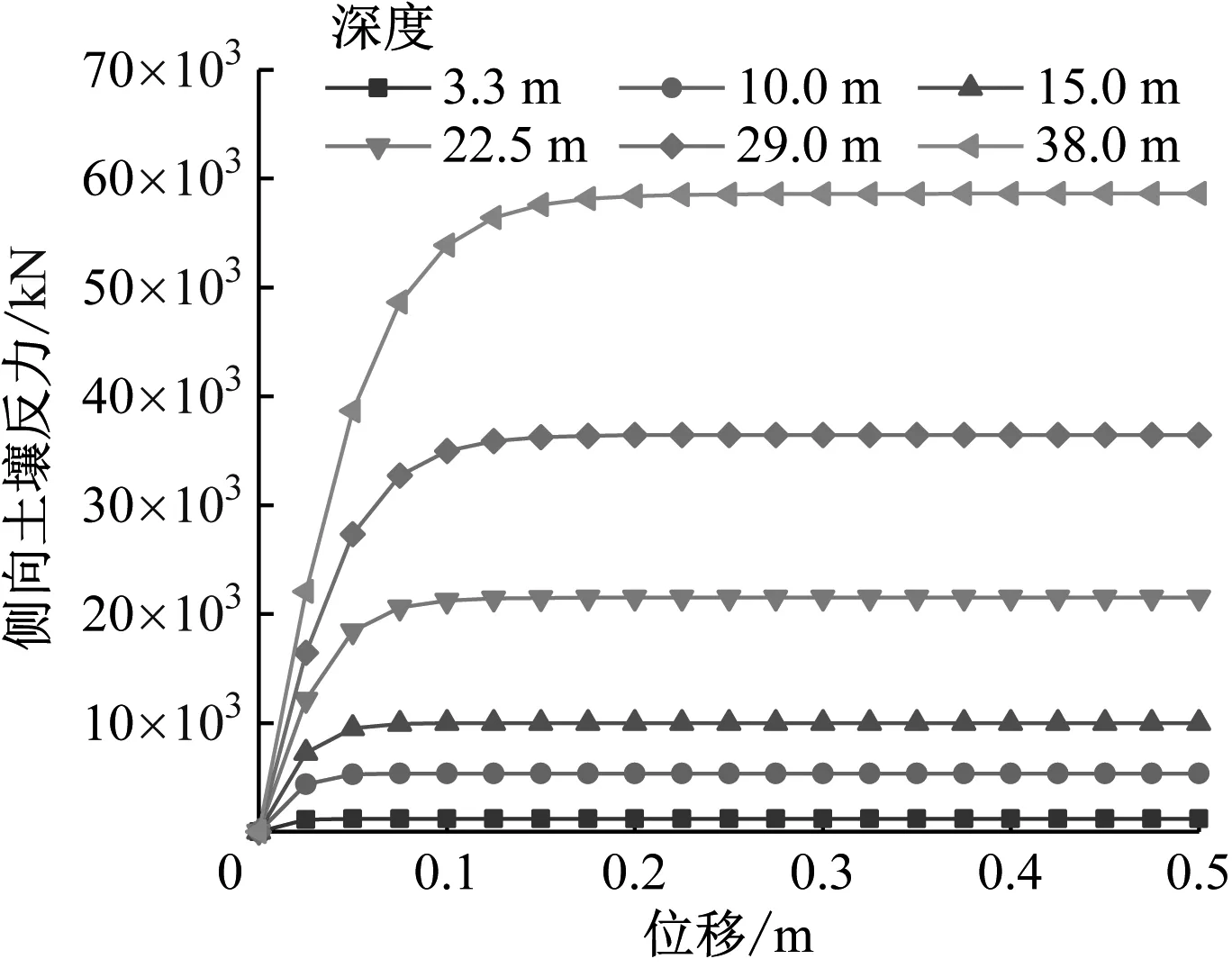
图6 不同深度下土壤的p-y曲线图
1.4 不同冲刷深度的有限元模型
通过减少海床以下土构-耦合弹簧来模拟不同冲刷深度,并计算塔架动态响应。图7为不同冲刷深度的简化模型。
(a) 未冲刷
2 风力机载荷
2.1 湍流模型
为准确计算湍流风场,基于IEC 61400—3设计准则[27],采用风力机开源软件OpenFAST计算轮毂高度处的风轮推力。湍流模型[28]为:
(9)
式中:XW(f)为来流方向功率谱密度的分量;Uhub为轮毂处平均风速;βW为不同方向上风速分量标准差;f为循环频率;LW为各风速分量积分尺度参数;下标W表示湍流风在x、y、z方向的风速分量μ、ν和ω。
速度分量积分尺度LW为:

(10)
(11)
式中:Q为湍流尺度参数;z为轮毂高度。
βW等于湍流强度与平均风速之比,不同分量之间关系为:
βν=0.8βμ
(12)
βω=0.5βμ
(13)
轮毂高度处平均风速为11.4 m/s的风速时域曲线变化如图8所示。

图8 湍流风场
2.2 波浪理论
莫里森方程是将单位长度合力表述为阻力与惯性力之和,其被广泛应用于海上圆柱形单桩波浪力,本文应用该方程求解风力机在海上的波浪载荷[29],表达式如下:
(14)
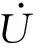
波浪大小由波高和波周期决定,Wan等[30]对我国近海波浪能进行了分析,并指出近海波浪能的有义波高通常为0.5~4 m,周期为4~10 s。根据实际海况,确定海况参数波高为4 m,波周期为7.2 s。
3 结果与分析
3.1 模态分析
模态是结构的固有特性,包括自振频率、阻尼和振型。考虑土-构耦合时塔架一阶和二阶前后向及侧向模态自振频率,表4给出了风力机塔架自振频率。
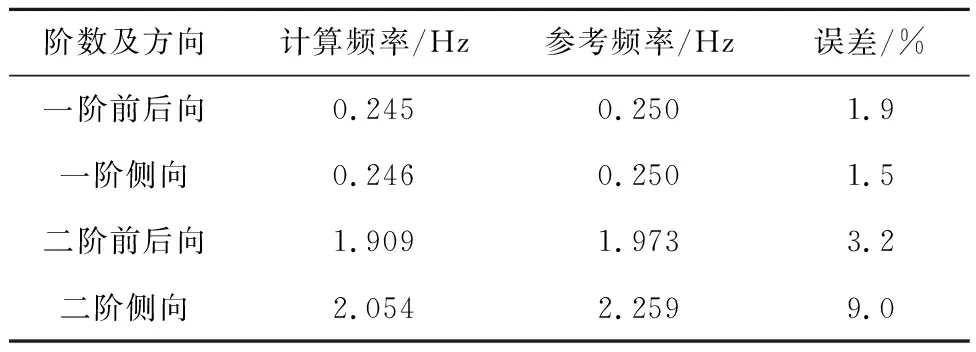
表4 塔架自振频率
与参考频率[21]相比,计算频率与参考频率的最小误差和最大误差分别为1.5%和9.0%,误差在工程允许范围内,故所建模型、网格划分和计算方法均准确有效。
为研究冲刷效应对风力机整机自振频率的影响,图9给出了系统整机自振频率的变化。随着冲刷深度的增加,各阶频率随之降低。对于未冲刷、冲刷深度分别为0.64D和1.28D时,一阶前后向自振频率依次为0.204 Hz、0.202 Hz和0.198 Hz,一阶侧向自振频率依次为0.207 Hz、0.206 Hz和0.200 Hz,故随冲刷深度的增加,一阶自振频率降幅较小,桩基冲刷深度对低阶频率影响有限。冲刷深度为1.28D时二阶前后向及侧向自振频率分别为1.231 Hz和1.245 Hz,较之未冲刷,自振频率分别减小9.39%和12.57%,随着冲刷深度增加,自振频率明显下降,说明冲刷效应对高阶自振频率的影响较大,设计时应注意风力机共振问题。
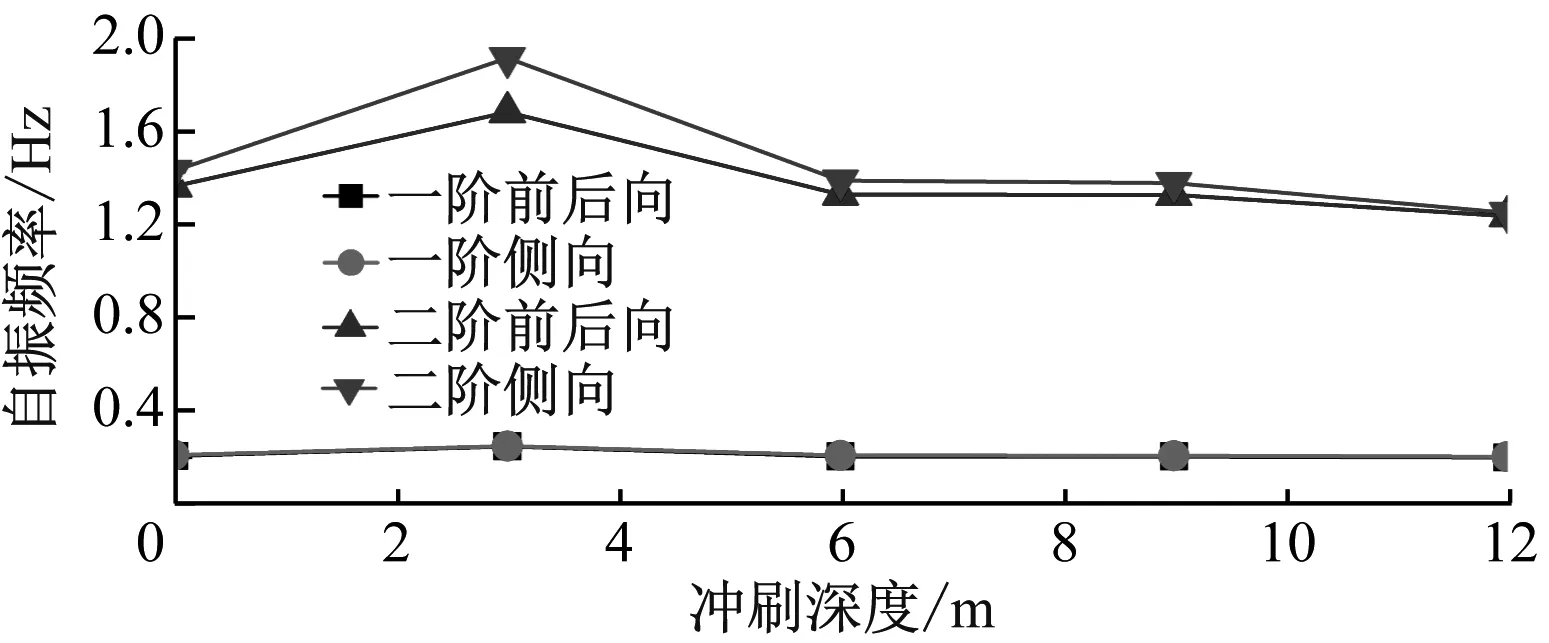
图9 风力机系统自振频率随冲刷深度的变化
3.2 瞬态分析
3.2.1 塔顶位移
塔顶是连接机舱和塔架的关键部位,发生冲刷后在环境载荷的影响下,风力机塔顶会产生剧烈振荡,进而出现局部动力学问题,直接影响整个风力机的运行安全。
图10为风力机塔顶位移时域曲线。在额定风况下,冲刷深度不同时塔顶位移曲线具有高度的相似性。随着冲刷深度的增加,塔顶位移响应时域曲线逐渐上升,在44.6 s左右达到峰值,此时未冲刷、冲刷深度分别为0.32D、0.64D、0.96D和1.28D时塔顶峰值位移依次为1.82 m、1.83 m、1.87 m、1.90 m和1.96 m。较之未冲刷,随着冲刷深度增加,塔顶位移依次增加0.7%、3.2%、4.5%和7.8%。当冲刷深度较小时,位移幅值增加较小,随着冲刷深度的增加,冲刷对塔架造成的影响越来越大。未冲刷和冲刷深度为0.32D时塔顶位移未超过结构位移极限,但随着冲刷深度的继续增加,塔顶位移急剧增大,越来越接近位移极限,设计时应重视。
3.2.2 桩基位移
在局部冲刷中,冲刷坑的产生使得桩基埋土深度减小,这对桩基水平承载性能的影响很大。笔者模拟实际海上单桩所受载荷,同时对其施加湍流风及波浪载荷,得到基础在泥面处的桩基位移。图11为桩基位移的时域曲线。
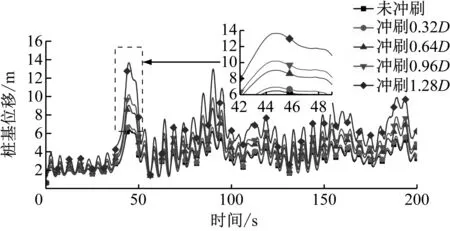
图11 桩基位移时域曲线
随着冲刷深度的增加,在环境载荷的影响下,桩基泥面处会产生较大的侧向位移,与风力机其他部位相比,桩基更容易受到冲刷坑的影响。因所施加风载荷为非定常湍流风,故整个桩基位移曲线在200 s内无明显规律。在44.6 s时不同冲刷深度下桩基位移均达到峰值,未冲刷、冲刷深度为0.64D和1.28D时桩基最大位移分别为6.47 mm、9.02 mm和13.62 mm,较之未冲刷,冲刷深度为0.64D和1.28D时桩基最大位移分别增大39.4%和110.5%。较之塔架部分,冲刷直接作用于桩基,故对桩基部分影响较大,随着冲刷深度的增加,位移幅值增加也越明显。当桩基位移达到设计位移允许值时,则认为达到桩基水平极限承载力。胡丹等[10]指出,在实际设计中泥面桩基位移允许值为0.2倍的桩径,未达到桩基设计极限,但随着冲刷深度的增加,桩基位移逐渐增大,越来越趋近于设计极限。
3.2.3 桩基应力
风力机运行时,环境载荷可能导致桩基等效应力过大,使风力机遭到局部破坏,造成一定的安全隐患。
图12为不同冲刷深度下桩基应力瞬态动力学响应曲线。在环境载荷作用下,风力机应力呈无规则波动,且在44.6 s处第1次达到峰值,此时未冲刷、冲刷深度分别为0.32D、0.64D、0.96D和1.28D时桩基应力依次为45.55 MPa、47.14 MPa、48.21 MPa、51.52 MPa和52.05 MPa。较之未冲刷,冲刷深度为0.64D和1.28D时桩基等效应力分别增大5.8%和14.3%。因此,冲刷会造成应力更加集中,对风力机结构动力学响应具有放大作用,设计时应注意应力集中问题。
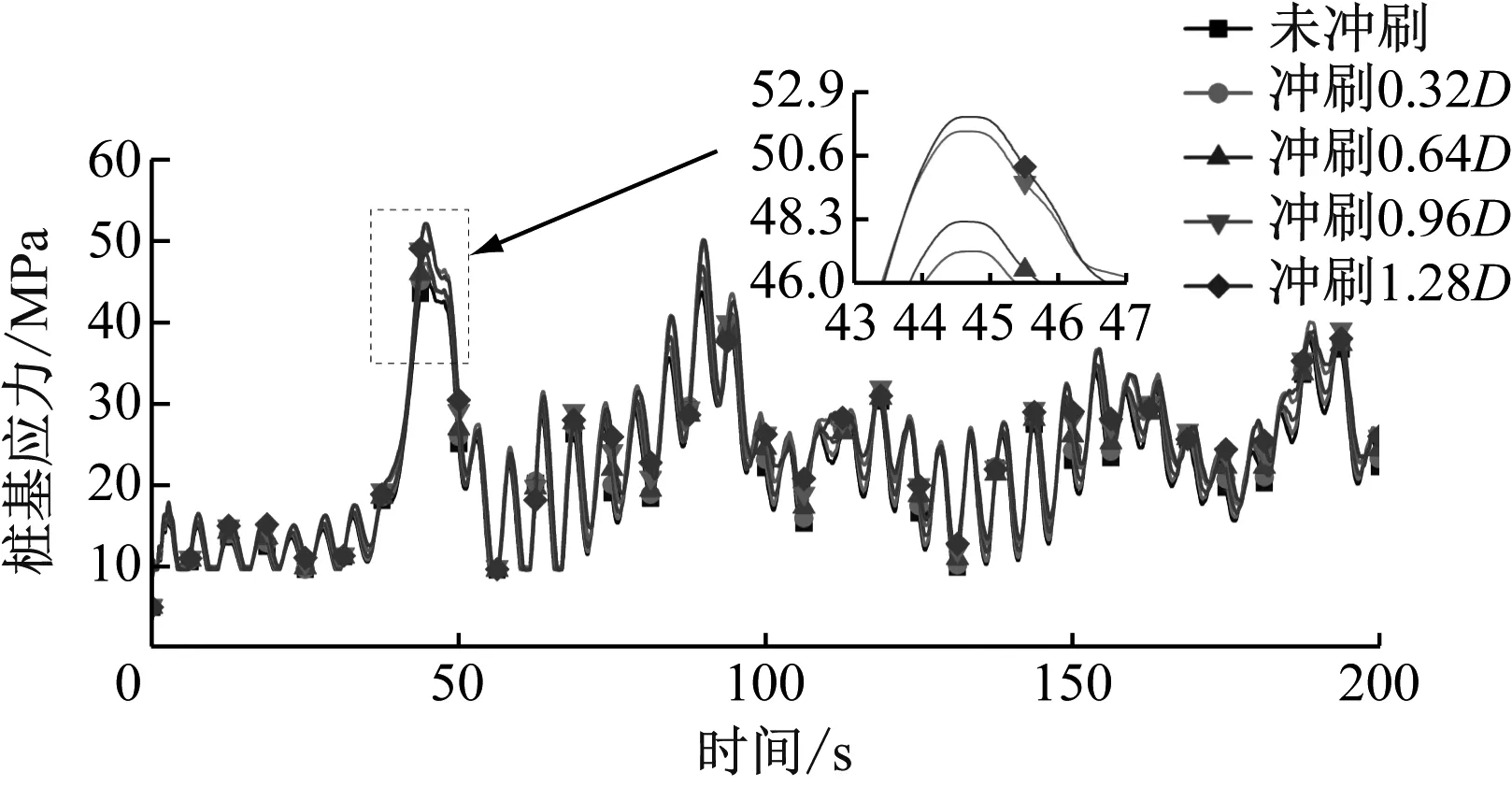
图12 桩基应力响应的时域曲线
3.2.4 应变能
风力机结构受到外界载荷激励影响时会产生形变,应变能因形变而储存在结构内,在未超过应力极限时,结构通过振动释放应变能,当应力超过弹性极限时,则会导致塑性变形。故应变能的大小对风力机的评估至关重要。
图13为风力机整机在不同冲刷条件下的最大应变能响应的时域曲线。在额定工况下,不同冲刷深度下塔架应变能在44.6 s处达到峰值,此时未冲刷、冲刷深度为0.64D和1.28D时应变能依次为4.05 kJ、4.18 kJ和4.32 kJ,较之未冲刷,冲刷深度为0.64D和1.28D时最大应变能分别增大3.1%和6.7%。随着冲刷深度的增加,塔架最大应变能逐渐增大,应注意冲刷现象,保证风力机在役期间安全有效运行,避免不必要损失。
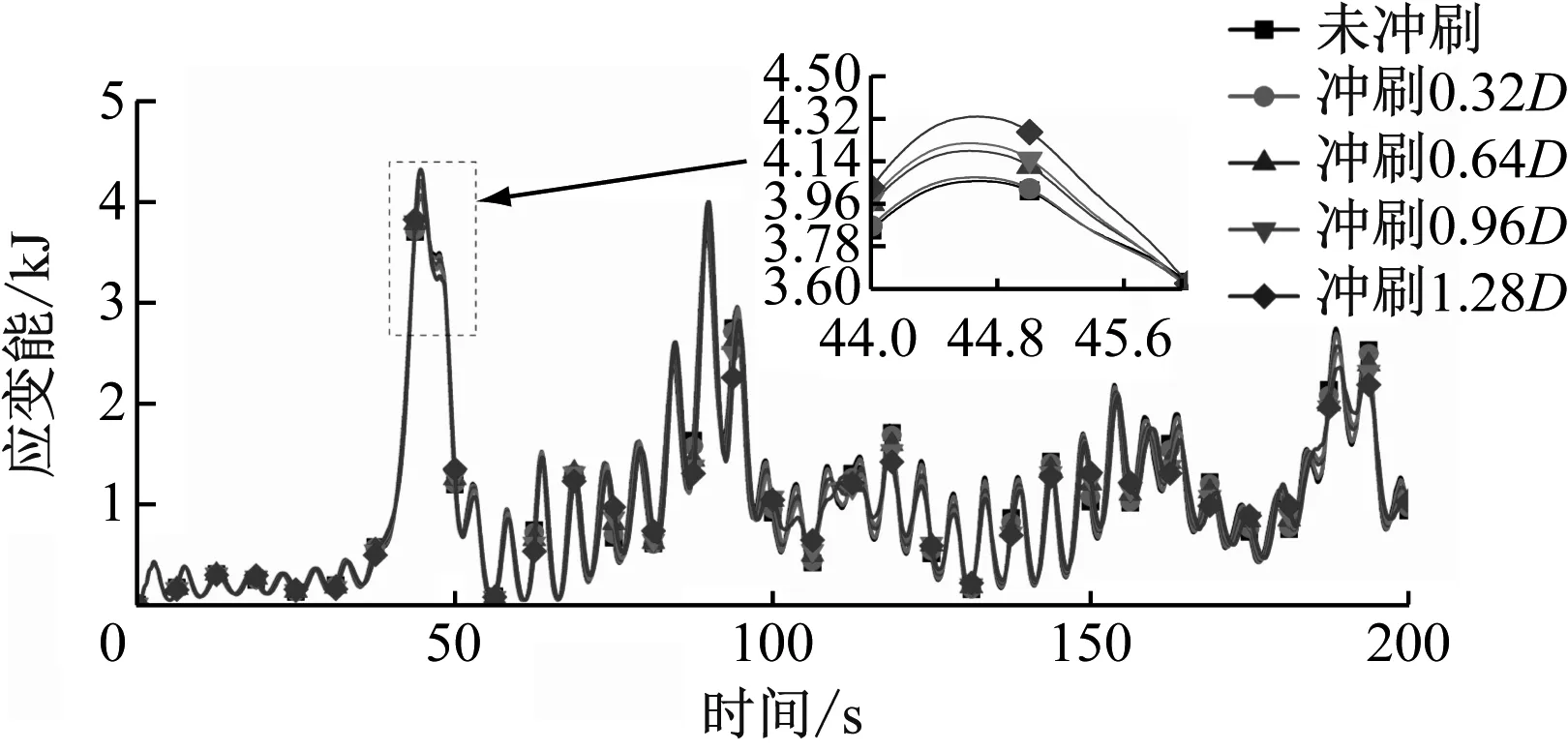
图13 最大应变能响应的时域曲线
4 结 论
(1) 随着冲刷深度的增加,冲刷对一阶自振频率的影响较小,二阶自振频率明显下降。当风力机自振频率接近环境载荷频率时结构会发生共振。
(2) 在环境载荷作用下,随着冲刷深度的增加,塔顶和桩基水平位移曲线不断增大。较之未冲刷,冲刷深度为1.28D时塔顶峰值位移增大7.8%,桩基位移增大110.5%。因冲刷发生在桩基附近,直接作用于桩基,故冲刷对桩基影响更大。
(3) 随着冲刷深度的增加,应力和应变能聚集愈加明显。较之未冲刷,冲刷深度为1.28D时最大应力增大14.3%,最大应变能增大6.7%。冲刷深度越大,应力和应变能峰值越大,导致风力机倒塌风险增加,设计时应充分预估冲刷对风力机的影响。
