双足竞赛机器人的动态步态规划设计与实现
2023-09-25许波朱楹唐雅媛
许波,朱楹,唐雅媛
(湖南科技学院 信息工程学院,湖南 永州 42519)
0 引言
双足竞赛机器人的步态规划,是指在机器人运行过程中按照行走条件要求的步态参数条件,通过合理控制时间和距离以实现机器人各个关节的稳定运动角度。而步态规划所要达到的最主要目标就是形成完美步态,即在一个行走时间内能够实现完全稳定运动的机器人腿部各个关节轨迹规划[1-3]。
研究人员通过分析人类的行走姿态,进行数据整理,根据人类行走步态的稳定性、高适应性等特点,最终实现仿生行走。其中,日本“WABIAN-2”机器人的拟人步态算法基于仿生原理并应用于机器人上[4]。三维线性倒立摆模型[5]作为目前使用最普遍的机器人步态研究模型,把机器人抽象看成由多个连杆与关节点组成,各关节之间通过具有刚性的连杆串联一起,形成刚性的连杆倒立摆。
本文以NAO 机器人[6]接力赛为例,为实现双足竞赛机器人快速、稳定的步态进行研究并解耦分析,通过起步、步中、止步三个阶段的步态规划得到合理稳定的步态轨迹,实现了一套针对机器人竞赛的动态步态规划系统。
1 双足竞赛机器人步态规划设计
1.1 起步、止步阶段步态规划
由于双足竞赛机器人是一个复杂的多自由度运动系统,要实现仿人双足行走运动,双足竞赛机器人下肢的自由度分配应尽可能与人的自由度分配相一致。在倒立摆的步态规划中,摆动腿摆动时,其支撑腿可以简化为绕支撑腿踝关节的摆杆。由于踝关节有两个自由度,因此步态规划时,要分开进行规划,即在前向和侧向分别进行步态规划。前向步态规划包括髋、膝和踝关节的两条腿6个俯仰自由度的规划,侧向步态规划包括髋关节和踝关节两条腿4个滚动自由度的规划,这样双足竞赛机器人一共有 12 个旋转自由度。设立三个步态周期T1、T2、T3 进行缓冲,三个步态周期为变加速运动。此时可以将质心在正向平面运动的方程拟合为:
其中,a、b、c、d分别为初始加速度,变加速运动的加速度、速度、初始位移。由于不能让机器人一开始就摔倒,需要X轴方向ZMP=0,即:
本文规定双步阶段完成时,髋关节偏移为最大值A,规定单步阶段髋关节逐渐回到中心,即侧向平面方程Z侧(t)=0,此时摆动腿抬至最高。止步阶段规划与起步阶段相反,这里不做赘述。
1.2 步中阶段步态规划
当机器人匀速运动时,机器人髋关节高度过高,机器人所受力矩变大,使得机器人运行不稳定,为使机器人速度增加,脚步交替次数增多、频率加快且稳定,需降低髋关节离地面高度,质心随之降低,同样也会增加腿部电机耗能,当髋关节位置合适时,将有利于机器人稳定行走,由倒立摆模型得到的机器人质心与机器人的关系,选定机器人行进时髋关节高度为:170 mm,即H=170。髋关节运动方程即为:
S0为相对于后脚在x平面上的距离,并且认为后脚初始位置为0,Sstep为机器人步长,T为跨越每步长所用时间,由于髋高固定,规定髋关节运动方程关于h是一个定值。
1.2.1 踝关节轨迹方程
本文选取机器人一个步态周期中有T1、T2、T3关键帧,其中摆动腿达到低点时刻为T1,此时为单步—双步阶段;摆动腿达到最高点时刻为T2,此时为双步—单步阶段;摆动腿又返回最低点时刻为T3,此时为单步—双步阶段;对应的最高点机器人摆动腿脚底离地面高度为h1,最低点摆动腿离地面高度为h2。一个步态周期对应着T1、T2、T3、T2、T1,五个关键帧,即双步—单步—双步—单步—双步为一步态周期。
由关键帧所对应的速度,高度,角度约束得出踝关节轨迹方程,所得轨迹方程在Desmos①上如图1、图2所示:Xx(t)方程图像、Xy(t)方程图像:
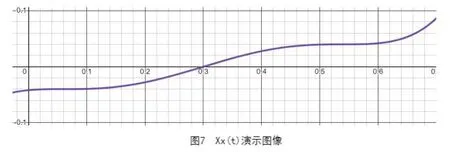
图1 Xx(t)演示图像
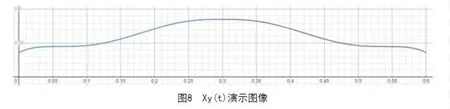
图2 Yx(t)演示图像
由上述可知,可将踝关节行进间抬脚的单步阶段轨迹拟合成正弦三角函数;双步阶段,摆动腿着地,轨迹认定为一条直线,将机器人跨域一个步长所用时间为T,则单步周期T 单大约视为整个周期的2/3,双步周期大约视为整个周期的1/3。
1.2.2 髋关节、膝关节轨迹方程求解
由于机器人腿部都有六个自由度,其中髋关节的位置与踝关节的位置能够确定腿部在某一时刻机器人其他关节的对应角度,即可以由髋关节所在空间的位置与踝关节在空间的位置确定其他角的位置,选用相对位置来计算。
当机器人腿部发生位移时产生x,y,z方向的偏移,由于支撑腿的存在,机器人髋关节高度相对地面固定,可以通过计算得知髋关节、膝关节、踝关节的角度的具体大小。Fx(t)为踝关节在x轴方向由轨迹方程所确定的位置;Fy(t)为在y轴方向由轨迹方程所确定的位置;Sx(t)为髋关节x轴方向由轨迹方程所确定的位置;Sy(t)为在y轴方向由轨迹方程所确定的位置,根据逆运动学求解[10]。
针对机器人双腿各个关节的关系,利用逆运动学分析转换为关节角序列,在Choregraphe②软件上完成程序设计,并移植到NAO机器人中进行实验、调试,以上述步态规划为基准,对相关参数进行手动调试,在局部范围内找到最优初始化参数,并在NAO竞速比赛场地进行试验。
2 实验结果与分析
经过动态步态的解耦分析,为验证其可行性,本文以NAO 机器人为例,采用Python2.7 进行程序设计并移植到Choregraphe进行实验,对此步态规划通过编程设计,在程序中得到机器人各关节序列组。
2.1 实验数据
通过实验测试得到设定双足竞赛机器人初始的髋关节高度为170 mm、重心的处置位置(相对于机器人后脚跟)46.5 mm、行进时两脚间距150 mm 是最合理的。然后通过调整单步周期、一个步态周期的时间、步长(机器人走两步)、摆动腿抬脚高,得到双足竞赛机器人脚部12个关节的扭转角度序列和对应的时间序列,代码实现后,实验测试机器人在行走过程中的速度与稳定性,得到以下数据:
表1 为实验测试中几组代表性的数据,由表1 可知,机器人步长控制在1/3左右步态周期最好,速度过快稳定性会降低,将机器人速度控制在22 cm/s 左右最好。
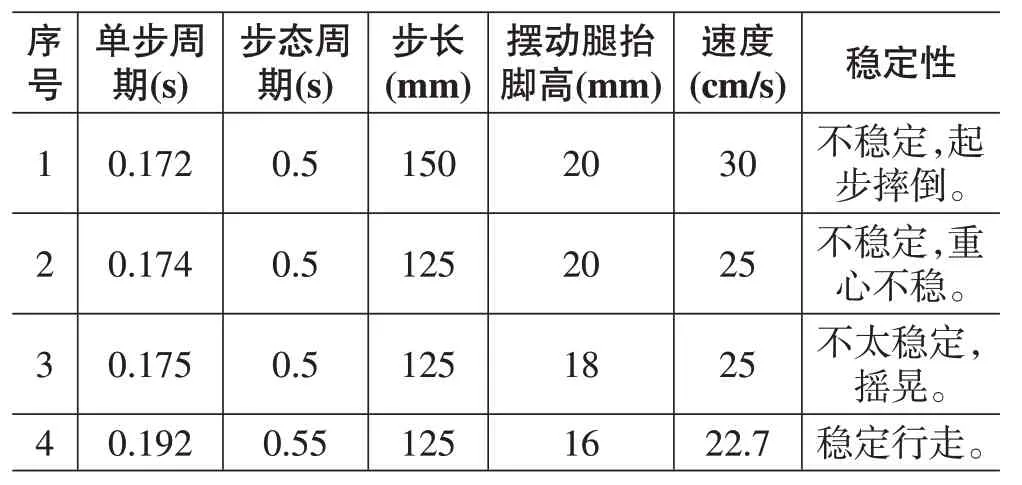
表1 机器人行走各项参数的速度与稳定性
2.2 关节角度规划曲线
将机器人运动过程中左右脚髋关节偏转(HipYawPitch)、髋关节滚动(HipRoll)、髋关节扭转(HipPitch)、膝关节扭转(KneePitch)、踝关节扭转(AnklePitch)和踝关节滚动(AnkleRoll)即12 个关节的角度序列在图形计算软件Desmos得到规划曲线,如图3所示。
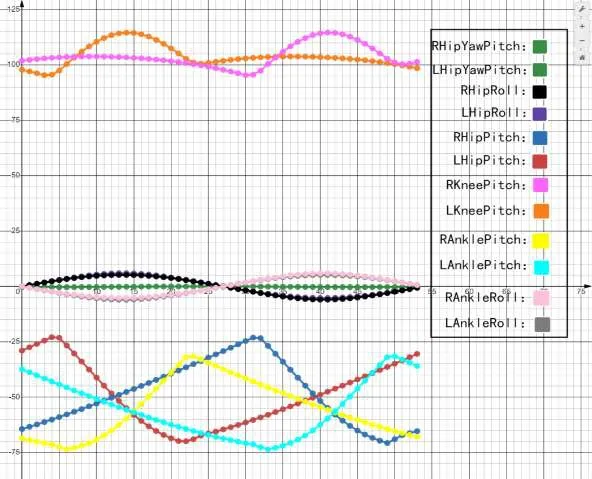
图3 机器人各个关节角度
2.3 实验分析
由关节角度规划曲线图可知整个步态中,各关节角度呈现周期性变化,关节变化需趋于光滑,为了与人类行走的规律相近,髋关节偏转(HipYawPitch)变化范围小,其他关节变化的范围大小几乎一样。机器人行走的十二关节角度规划图如图3所示,各关节在行走过程中协调配合,笔者将实验数据通过代码实现移植到NAO机器人运行,得到现实机器人行进过程中在choregraphe 上1:1 仿真模拟图,截取关键帧T1—T2—T3—T2—T1 五个关键帧,即为一个步长的关键帧,如图4所示。
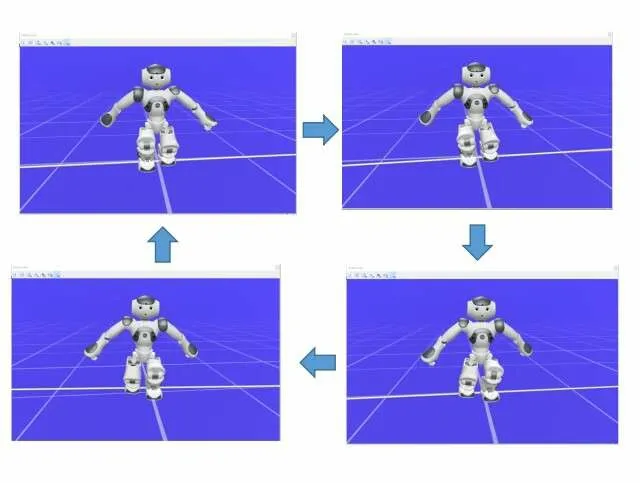
图4 机器人关键帧仿真图
通过关节角度规划图和Choregraphe 软件上的仿真模拟图获得的实验数据,验证了步态规划的可行性,使机器人行走速度达到20 cm/s以上,最高可达25 cm/s,大大增加了机器人在竞赛中行走的速度,在提高机器人行走速度的同时,能让机器人保持稳定性。同样,此类步态规划能够通过调节髋关节高度、步长和步伐频率得到想要的速度,能够在各类竞赛中得到应用,例如:机器人高尔夫比赛、机器人足球比赛和机器人接力赛。
3 结论
本文以NAO机器人接力赛为背景,提出了一种适应双足竞赛机器人的步态规划方案对机器人行进过程中起步、步中、止步三个步态周期进行动态步态规划,并运用拉格朗日插值拟合机器人关节曲线,通过在choregraphe软件上的仿真实验,最终成功实现了机器人接力赛中快速、稳定地行走,由此,未来可将此种步态改进以适应各类双足竞赛机器人的比赛。
注释:
① Desmos是一个数学图形计算工具。
② Choregraphe 是一款用于连接NAO 机器人的可视化编程软件。
