基于信息扩散理论的气象灾害风险分析方法研究

钟平晖 余斌 陈金鑫 伍昕 王也 陈水明

（1.五凌电力有限公司，湖南长沙 410004；2.湖南五凌电力科技有限公司，湖南长沙 410004；3.上海远景科创智能科技有限公司，上海 200000）

1 引言

气象灾害作为自然灾害的一种，对农作物、动物、植物等具有较高的危害，常见的气象灾害有洪涝、干旱等，从全球范围来看，根据某组织对气象灾害数据统计，在2010—2015 年间全世界共发生了5 642 次气象灾害，造成的直接经济损失达到2.65万亿元，人员伤亡数量高达251 万人次，其中人员死亡数量为148 万人次［1］。气象灾害造成的直接经济损失占国民生产总值的0.25%，对于低收入国家而言，这个比例还会更高。受全球气候变暖影响，在未来气象灾害发生概率和频次还会有所增加，与此同时也会带来极大的风险。为了制定有效的方案和采取相应的管理措施，需要对气象灾害风险进行高精度分析，以此控制气象灾害风险，降低气象灾害带来的损失。气象灾害风险的分析需要大量的历史灾情信息，而历史灾情信息存在严重的不足，导致对其分析具有较高的难度。国内已有相关专业的研究人员开始针对气象灾害风险加以分析。刘志萍等人采用模糊综合评价法，针对气象灾害危险性特征进行分析和风险区划，对气象灾害按照权重进行排序，分析致灾因子危险性，为作物种植提供技术支持［2］。在实际应用过程中，虽然能够有效地对气象灾害危险性特征进行分析，但是该方法分析样本数据体积较小，导致分析结果与实际情况的相关系数比较低，降低了分析结果的可信度，难以对实际区域的气象灾害进行详细、具体的分析，无法满足实际需求。

信息扩散理论是为了弥补信息不足而出现的一种模糊数学处理方法，把模糊问题转换为确定性问题，主要是针对样本模糊信息中的样本进行集值优化，可将信息扩散理论应用到高温热害、旱灾、洪水、霜冻、风等风险的分析中。因此，本文基于信息扩散理论，设计一种气象灾害风险分析方法。

2 气象灾害风险分析方法

2.1 气象灾害风险因子筛选

气象灾害风险主要来源于致灾危险性、承灾体脆弱性、承灾体暴露性以及区域防灾抗灾能力4 个方面，因此选取这4 个因素作为气象灾害风险因子。其中，致灾危险性的大小与气象灾害发生频次和致灾因子强度有关，其计算公式为：

式中，R 表示致灾危险性；F 表示致灾因子强度，即近5 年或者近10 年发生的气象灾害的最高强度；P 表示区域气象灾害发生的频率。

根据该区域气象站点记录的历史气象数据，可计算出其气象灾害发生频率，其计算公式为：

式中，n 表示该区域发生气象灾害的年数；N 表示气象站点有可用气象数据的总年数。

气象灾害虽然具有一定的危险，但是其产生的风险与承灾体的脆弱性和暴露性有直接关系，承载体越脆弱，暴露面积越大，气象灾害风险越高［3］。

承灾体的脆弱性可以用区域产量变异长度来表示，其公式为：

式中，V 表示承灾体脆弱性指数；Ymax表示气象灾害风险分析区域多年单产最大值；Y 表示该区域某年的单产量；m 表示区域单产资料总年份数［4］。

承灾体的暴露性是指承受气象灾害的主体暴露于孕灾环境的程度，其暴露程度越大，气象灾害损失也就越大，气象灾害风险越高［5］。受气象灾害影响最大的主要为农作物，根据区域农作物种植面积以及区域总面积，计算出承灾体的暴露性，其计算公式为：

式中，E 表示承灾体的暴露性指数；B 表示区域农作物种植面积；S 表示区域总地理面积。

正常情况下，为了抵抗气象灾害，区域会采取一些预防措施和减灾措施，以此提升自身的防灾减灾能力，该能力越高，气象灾害风险越低，因此区域防灾减灾能力与气象灾害风险也有着十分密切的关系。区域防灾减灾能力主要受人为因素影响，人为因素包括农民人均可支配收入、人均非家庭经营收入占比、农业从业人员占比、单位种植面积农业机械总动力、耕地有效灌溉面积比例以及单位面积化肥施用量。利用以上6 个指标评价区域防灾减灾能力，其用公式表示为：

式中，X 表示区域防灾减灾能力；n 表示区域防灾减灾能力评价指标数量；w 表示归一化系数；x 表示农民人均可支配收入；e 表示人均非家庭经营收入占比；s 表示农业从业人员占比；a 表示单位种植面积农业机械总动力；c 表示耕地有效灌溉面积比例；q表示单位面积化肥施用量。

2.2 基于信息扩散理论的样本数据集值化处理

选取区域所有气象站记录的历史气象灾害数据作为数据样本，考虑到气象灾害数据量并不丰富，样本容量比较小，因此以信息扩散理论作为理论依据，对样本数据进行扩散处理，将样本数据转换为一个模糊集，通过对模糊集非正态扩散，扩大样本数据量，将样本信息扩散到整个气象灾害风险指标论域中所有点上，增加样本数据容量，扩大样本数据体积，为气象灾害风险分析提供丰富的数据基础。

按照上文筛选的气象灾害风险因子建立风险因素指标序列，假设YN为第N 年发生气象灾害的观测样本，构建气象灾害观测样本集合：

式中，Z 表示气象灾害观测样本集合［6］；YN为第N年发生气象灾害的观测样本；N 为年数。

信息扩散过程遵守信息量守恒的原则，气象灾害观测样本集合中任意一个观测样本Y 都要落在扩散区间内，假设扩散区间为［a1，am］，气象灾害风险因子指标论域为U，其用公式表示为：

将携带的信息扩散到气象灾害风险因子指标论域U 中的所有点，其用公式表示为：

式中，f 表示信息扩散后的气象灾害数据集；h 表示信息扩散系数。

根据区域气象灾害年发生次数的最大值和最小值计算该系数h，其计算公式为：

式中，b 表示区域气象灾害年发生次数的最大值；a表示区域气象灾害年发生次数的最小值；k 表示气象灾害样本数量。

按照上述流程对选取的样本数据进行扩散，将信息点扩散到气象灾害风险因子指标论域上。

2.3 气象灾害风险定性分析

考虑到每个气象灾害风险因子对气象灾害风险影响程度不同［7］，因此在上文基础上，利用层次分析法计算出各个气象灾害风险因子权重，风险因子权重计算公式为：

式中，ω 表示气象灾害风险因子权重值；n 表示气象灾害风险因子数量；εn表示第n 个气象灾害风险因子对气象灾害风险的贡献度；κn表示第n 个气象灾害风险因子的标度值。

气象灾害风险因子标度值评价规则为：如果两个风险因子相比，前者比后者强烈重要，则风险因子标度取值为1；如果两个风险因子相比，前者比后者极其重要，则风险因子标度取值为3；如果两个风险因子相比，前者比后者一般重要，则风险因子标度取值为5；如果两个风险因子相比，前者与后者同等重要，则风险因子标度取值为7［8］。按照该规则确定各个风险因子标度值，将其代入公式（10）中，得到风险因子权重值。利用评价函数计算出气象灾害风险指数：

式中，K 表示气象灾害风险指数；ωr表示致灾危险性权重值；ωv表示承灾体脆弱性权重值；ωe表示承灾体暴露性权重值；ωx表示区域防灾减灾能力权重值。

将信息扩散后的数据代入公式（11）中，计算出区域气象灾害风险指数［9］。根据气象灾害风险分析实际需求，此次设计了5 个风险等级［10］。气象灾害风险指数取值范围为0～1，如果公式（11）计算结果小于0.2，则表示该区域气象灾害风险等级为一级，风险程度为低风险，区域防灾减灾能力强、灾害危险性低；如果公式（11）计算结果大于0.2、小于0.4，则表示该区域气象灾害风险等级为二级，风险程度为较低风险，区域防灾减灾能力较强、灾害危险性较低；如果公式（11）计算结果大于0.4、小于0.6，则表示该区域气象灾害风险等级为三级，风险程度为中度风险，区域防灾减灾能力一般、灾害危险性一般，需要完善和修改气象灾害预防方案，提升气象灾害防御能力，降低气象灾害风险；如果公式（11）计算结果大于0.6、小于0.8，则表示该区域气象灾害风险等级为四级，风险程度为较高风险，区域防灾减灾能力比较弱、灾害危险性比较高，需要采取有效的措施，控制气象灾害风险；如果公式（11）计算结果大于0.8，则表示该区域气象灾害风险等级为五级，风险程度为高风险，区域防灾减灾能力非常弱、灾害危险性非常高，需要加大自身防御能力，作出正确决策，加大气象灾害抵抗力度。根据以上评价标准，对气象灾害风险进行定性分析，确定气象灾害等级，以此实现基于信息扩散理论的气象灾害风险分析。

3 实验论证

为了验证本文提出的气象灾害风险分析思路的可行性与可靠性，设置对比实验对设计方法进行了测试。

3.1 实验设置

以某地区作为实验对象，以大风天气为例，选取该地区2011—2021 年气象数据作为数据样本，共1.26 GB；根据该区域统计信息网2011—2021 年的农业数据，得到该区域播种面积及总产量数据，共1.36 GB。该区域平均大风日数年变化趋势如图1 所示。

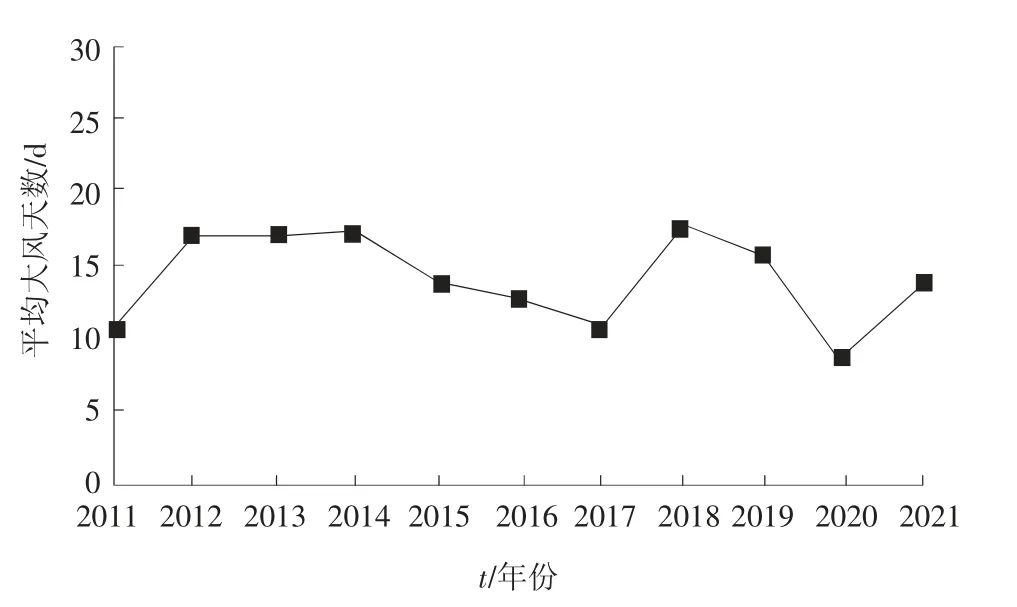
图1 2011—2021 年某地区平均大风日数年变化趋势

2011—2021 年某地区播种面积及总产量数据见表1。

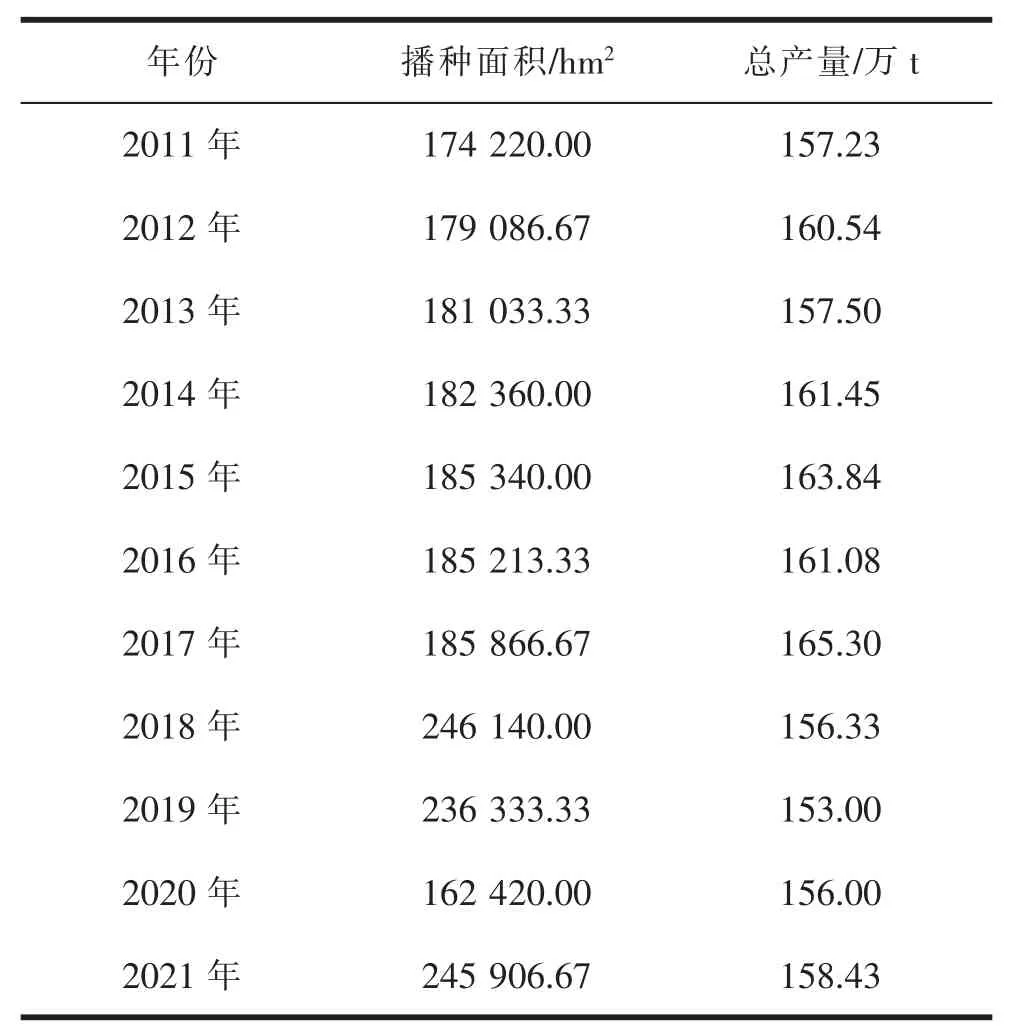
表1 播种面积及总产量数据

利用本文设计方法与文献［2］提出的基于模糊综合评价方法对该地区气象灾害风险进行分析。

3.2 实验过程

按照上述流程对收集的样本数据扩散处理，经信息扩散后得到数据12.64 GB。利用公式（10）对各个气象风险因子权重进行计算，其中对气象灾害风险影响程度最高的风险因子为致灾危险性，其权重值为0.56，承灾体暴露性和脆弱性次之，其权重值分别为0.46 和0.31，区域防灾减灾能力对气象灾害风险影响程度最小，为0.24。

3.3 实验结果与分析

根据对该区域大风与农业数据的分析，通过本文设计方法可分析出大风天气的频繁程度对粮食总产量具有一定的影响。大风天气数量较多的年份，该区域的年粮食总产量会出现不同程度的下降。虽然粮食总产量与播种面积有一定关系，但是同样也容易受到恶劣天气的影响，导致该年粮食总产量出现一定程度的降低。

为了验证本文设计方法分析的有效性，与传统方法进行对比，计算气象灾害风险分析结果与实际情况的相关系数。实验共分为8 组，利用MATLAB软件计算出两种方法分析结果与实际情况相关系数，相关系数越大表示气象灾害风险分析精度越高，将其作为两种方法评价指标，使用电子表格对实验数据进行记录，具体数据见表2。

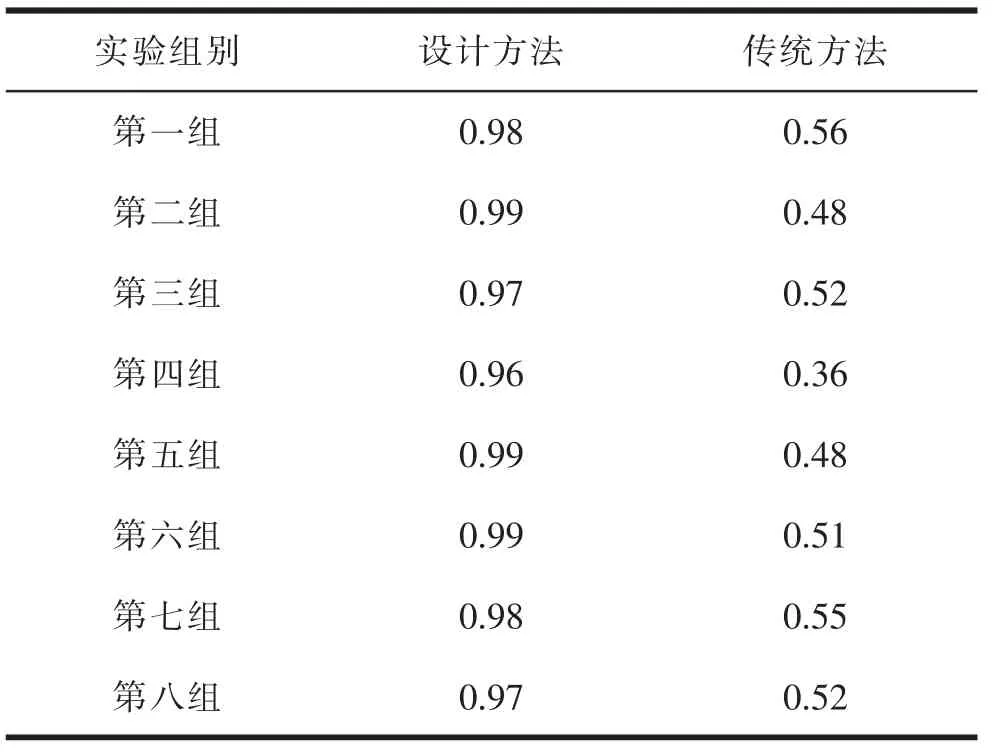
表2 两种方法分析结果相关系数对比

从表2 中数据分析可以得出以下结论：设计方法分析结果与实际情况相关系数较高，平均相关系数为0.97，最小相关系数为0.96，最高相关系数可以达到0.99，数值接近1，说明设计方法分析结果与实际气象灾害风险情况基本一致；而传统方法分析结果与实际情况相关系数比较低，平均相关系数仅为0.49，最大相关系数为0.56，最小相关系数为0.36，远远低于设计方法。因此实验结果证明，在精度方面，设计方法优于传统方法，其相比较传统方法更适用于气象灾害风险分析，分析结果具有较高的可信度，在气象灾害风险分析方面具有良好的应用前景，能够为气象灾害风险分析提供有力的理论支撑。

这是由于本文设计方法以信息扩散理论作为理论依据，对样本数据进行扩散处理，将样本数据转换为一个模糊集，通过对模糊集非正态扩散，扩大样本数据量，将样本信息扩散到整个气象灾害风险指标论域中所有点上，增加样本数据容量，扩大样本数据体积，提高了分析结果与实际情况相关系数，为气象灾害风险分析提供了丰富的数据基础。

4 结论

本文针对传统方法存在的不足，将信息扩散理论应用到气象灾害风险分析中，提出了一个新的气象灾害风险分析思路。

（1）筛选气象灾害风险因子，并对因子数据信息进行集值化处理，通过层次分析法评价气象灾害风险因子权重，确定气象灾害等级。

（2）通过实验证明，设计方法分析结果与实际情况相关系数平均值为0.97，具有较高的可信度，有助于提高应对气象灾害的响应时间，在一定程度上减少气象灾害带来的经济损失。

（3）由于研究时间的限制，本文提出的方法尚未在实际中进行大量应用和实践操作，因此在未来的研究中，可将本文设计方法投入实际气象灾害风险分析项目中进行长期的实验，并在实验中不断完善设计方法，以期为气象灾害风险分析提供有力的理论支撑。