面向3D-CNN的算法压缩-硬件设计协同优化

钱佳明，娄文启，宫 磊，王 超，周学海

1.中国科学技术大学计算机科学与技术学院，合肥230027

2.中国科学技术大学苏州高等研究院，江苏苏州215123

随着大数据时代的来临和计算机运算能力的提高，2D-CNN在图像分类方面取得了最先进的精度。然而，在处理视频等高维数据时，基于图像的2D-CNN无法对其中的时间信息和运动模式进行建模，因此无法取得令人满意的效果。为了实现对视频等高维数据的精确分类，研究人员提出使用三维卷积来捕获视频等数据中的时空信息。2010年，Ji等人首次提出了三维卷积神经网络[1]，其在相邻的图像帧上执行三维卷积以提取时间和空间维度上的特征。随后，Tran等人提出了一个现代意义上的深度架构C3D[2]，C3D 相对于以往的3D-CNN 具有更深的层，故而可以在大规模数据集上进行学习并取得最优的结果。此后，3D-CNN 在视频分析、三维几何数据分析、三维医学图像诊断方面取得了巨大的成功[3-5]。然而，与算法性能提升相对应的是3D-CNN显著增加的模型尺寸和计算量。例如，在网络结构相同的情况下，3D ResNet-34[6]的参数数目和计算量分别为6.35×105和36.7 GFLOPs，是2D ResNet-34（参数数目2.15×105，计算量3.5 GFLOPs）的2.95倍和10.49倍。相比于2D-CNN，3D-CNN 额外增加了时间维度以捕获时域特征，因此3D-CNN的部署存在更为庞大的存算开销。

针对这一问题，研究者在传统ASIC 和FPGA 专用AI 加速器设计的基础上[7-12]，提出了一系列软硬件协同优化方法，在算法端对3D-CNN 模型的计算复杂度、存储开销进行优化，并在硬件端设计与算法端适配的计算核心，以求达到更优的硬件部署效率[13-17]。其中，Sun等人对3D-CNN进行稀疏化处理[13]，通过裁剪冗余权值减少模型的计算和存储开销。然而，剪枝操作引入了计算和访存的不规则性，在导致额外硬件设计开销的同时也使得硬件加速器难以获得理想的性能提升；3D-VNPU[14]和F3D[15]分别采用了3D Winograd与3D FFT变换来减少卷积操作的计算量。尽管快速算法未引入不规则性，但其只对模型计算复杂度进行了优化而未降低模型访存需求。此外，该类方法对卷积核大小敏感，也限制了其应用场景。例如，两者都无法加速1×1×1卷积，这在现代网络中占据了主要计算量，如3D ResNet、3D MobileNet；Wu 等人提出了一种混合张量分解策略[16]，该策略对卷积层使用Tensor Train分解，对全连接层使用Hierarchical Tucker 分解，取得了比单一分解方法更好的压缩效果。然而，这类基于低秩分解的压缩方法往往会使模型的训练过程变得更加复杂，并且同样无法有效应用于小卷积核。总的来说，相关工作仍未妥善解决3D-CNN的处理效率问题，使其在能效/资源受限场景下的部署仍面临严峻的性能和能效挑战。

针对上述挑战，本文基于FPGA提出了面向3D-CNN高效硬件部署的算法-硬件协同设计与优化方法3D FCirNN。在算法层面，为了缓解以往稀疏化带来的不规则性，本文首次采用分块循环矩阵来压缩3D-CNN的权重，配合FFT 的加速，进一步将计算复杂度从O(N2)减少为O(NlbN)。此外，为缓解FFT 在不同网络层加速过程中所引入的时域/频域切换开销，本文引入了频域内的激活、批归一化和池化层，实现了全频域计算。在硬件层面，本文基于FPGA平台设计了一个和算法端适配的高效硬件架构，并针对片外访存效率、实数序列FFT 后复数的运算特点，提出了一系列面向硬件资源、内存带宽的优化措施，显著提升了模型硬件部署的性能和计算效率。本文的主要贡献如下：

（1）本文首次引入分块循环矩阵对3D-CNN进行压缩，并采用快速傅里叶变换进行加速，在精度损失较小的情况下，取得了相当可观的加速效果。在此基础上，为了消除由于FFT 所引入的频繁的时域/频域切换开销，本文进一步引入了频域中的激活、批归一化以及池化层，实现了全频域推理。

（2）本文在FPGA平台上实现了一个高效的硬件加速器。在访存方面，通过对特征图进行NC/8DHW8 格式的数据重排，显著提升了片外访存效率；在硬件资源方面，通过充分挖掘实数序列FFT 的特点，以及Xilinx DSP Slice的计算能力，进一步减少了资源占用，提升了加速器的性能。

（3）在Xilinx ZCU102 FPGA 上的实验表明，相较于以往最先进的工作，3D FCirCNN可以在精度损失可接受的范围内，取得接近32 倍的压缩比，以及16.68 倍的性能提升和16.18倍的计算效率提升。

1 背景知识

1.1 3D-CNN

先前的工作表明，3D-CNN目前在视频理解等领域已经达到了最先进的精度。然而，和2D-CNN 不同的是，为了提取时空信息，3D-CNN 在二维卷积的基础上增加了一个时间维度，形成了三维卷积。如图1 所示，在三维卷积中，卷积核不仅会沿着输入特征的空间维度滑动（R、C方向），也会沿着输入特征的时间维度（D方向）滑动，因此，三维卷积可以同时捕获输入特征的时空信息，相较于二维卷积具有更强的特征提取能力。假设输入视频In的空间分辨率为R×C，共有D帧（时间维度）和N个通道，权重W的卷积核数目为M，每一个卷积核的空间尺寸为Kr×Kc，时间尺寸为Kd，通道数目为N，则输入和权重进行三维卷积，会得到一个空间分辨率为(R-Kr+1)×(C-Kc+1)，时间维度为D-Kd+1，通道数目为M的输出特征图Out，其计算过程可由公式（1）所描述：

图1 三维卷积操作Fig.1 3D convolutional operation

显然，二维卷积是三维卷积在D=1、Kd=1 情况下的特例。分析可知，三维卷积的计算复杂度为M×N×D×R×C×Kd×Kr×Kc，存储开销为M×N×Kd×Kr×Kc。因此，相对于2D-CNN，3D-CNN 在模型大小方面增长了Kd倍，在模型计算量方面增长了D×Kd倍，计算量的增长相对于模型大小的增长更加显著，故三维卷积是一个更加计算密集的算法。例如，在C3D[2]模型中，卷积层占了整个网络计算量的99.8%以上。

在3D-CNN中，全连接层具有和2D-CNN相同的计算模式。假设全连接层输出特征a和输入特征x的维度分别为M、N，权重W是一个M×N的矩阵，不考虑偏置，则全连接层的计算可以表示为一个矩阵-向量乘法，即a=W⋅x，其计算复杂度和存储开销均为M×N。和三维卷积不同的是，在3D-CNN 中，全连接层的计算量占比较小，但却占据了大部分的存储开销，是整个网络的存储瓶颈。

1.2 循环矩阵

循环矩阵（circulant matrix）是一种特殊形式的托普利兹矩阵（Toeplitz matrix），一个N×N的矩阵A是一个循环矩阵，当且仅当其每一行元素都是上一行元素循环右移一个位置的结果，如图2（a）所示，用数学公式描述，就是A[i][j]=A[(i+1)%N][(j+1)%N]。根据该性质可知，只需存储A矩阵的第一列元素（称A矩阵的第一列元素所构成的向量为该循环矩阵的生成向量），就可以表示整个矩阵，从而将存储开销由O(N2) 减少为O(N)。此外，循环矩阵在带来O(N)倍压缩比的同时，还可以有效降低矩阵-向量乘法的计算复杂度：根据循环卷积定理[18]，一个N×N的循环矩阵A和一个N×1的任意向量x相乘，可以通过公式（2）进行加速：

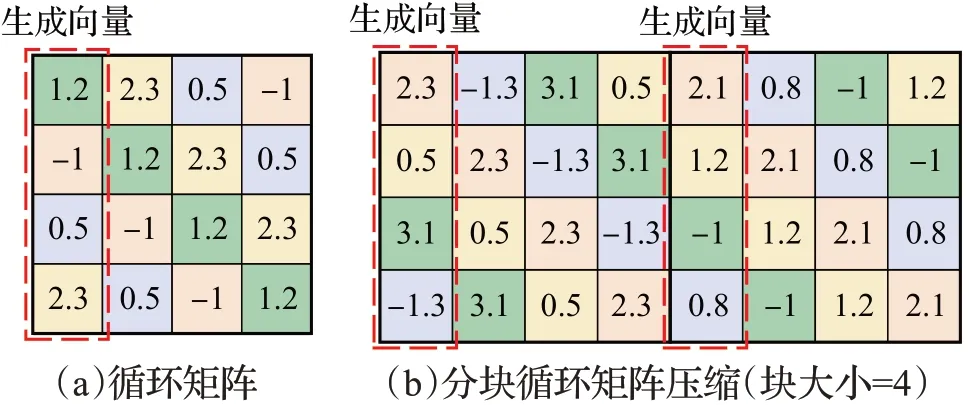
图2 循环矩阵及其压缩方法Fig.2 Circulant matrix and its compression method

其中，a是循环矩阵A的生成向量，FFT、IFFT分别表示快速傅里叶变换及其逆变换，⊙表示元素级乘法，如图3所示。注意到N点FFT/IFFT的计算复杂度为O(NlbN)，因此，通过循环卷积定理，可以将原先O(N2)的计算复杂度减少为O(NlbN)，从而取得O(N/lbN)倍的计算压缩比。

图3 循环矩阵-向量乘法的FFT加速Fig.3 FFT acceleration of circulant matrix-vector multiplication

根据定义，循环矩阵必须为方阵（即矩阵行数等于列数）。然而，在绝大多数情况下，矩阵往往不具备这一形式，因此无法直接用循环矩阵进行压缩。对此，可以通过分块来解决这一问题。该方法首先对矩阵进行分块操作，例如图2（b）中4×8 的矩阵被划分为2 个4×4 的子矩阵，然后令每一个子矩阵都具有循环矩阵的结构，则根据循环矩阵的性质，只需存储每一个循环矩阵的生成向量即可（图2（b）中红框内的4×2个元素），从而起到4倍（等于分块大小）的压缩效果。显然，在该压缩方法中，压缩比由矩阵的分块大小决定。因此，可以通过调节矩阵的分块大小，在精度和压缩比之间进行权衡：分块越大，其所能提供的压缩比则越大，而由此带来的精度损失也越大，反之亦然。

由于循环矩阵可以有效降低矩阵的存储和计算开销，一些研究人员开始将该方法应用于神经网络的压缩中[19-21]。Zhao 等人从理论上证明了循环矩阵在压缩深度学习模型方面的有效性[22]：在神经网络理论中，通用近似性质（universal approximation property）是指在参数数目足够多的情况下，神经网络以任意的精度逼近任何连续或可测函数的能力，这一性质为神经网络解决一系列机器学习问题提供了理论保证。Zhao 指出，采用分块循环矩阵压缩后的神经网络仍然具有这一性质，并且该结论可以进一步推广到更一般的低位移秩矩阵神经网络。

2 基于循环矩阵压缩的3D-CNN算法优化

2.1 全连接层的压缩

在3D-CNN 中，全连接层可以表示为矩阵-向量乘法操作。假设输入特征x和输出特征a的维度分别为N、M，则权重W为一个M×N的矩阵。为了使用循环矩阵对全连接层进行压缩，首先将权重W划分为p×q个B×B尺寸的子矩阵Wij（这里p=M/B，q=N/B，i=0,1,…,p-1，j=0,1,…,q-1）。令每一个子矩阵Wij均为循环矩阵，对应生成向量为wij。此时，对于所有的权值子矩阵Wij，仅需存储其各自对应的生成向量wij，因此总的存储开销为pqB，相较于未压缩时MN(pqB2)的存储开销，可以获得B倍的压缩收益。与上述压缩方法相对应，当使用压缩后的权重W与维度为N×1 的输入特征x进行计算时，对应需要将x划分为q个尺寸为B×1 的子向量xj，同理尺寸为M×1 的结果向量a将被划分为p个B×1 的子向量ai，分别计算，如公式（3）所示：

在此基础上，考虑到Wij为循环矩阵，其对应的生成向量为wij，故矩阵向量乘法Wij⋅xj可以进一步采用FFT进行加速，相应的ai计算过程如公式（4）所示：

为了进一步减少IFFT的调用次数，可以利用FFT/IFFT的线性性质[23]，将IFFT移至求和符号外，如公式（5）所示：

从而将IFFT的调用次数由q减少为1。综上所述，经过分块循环矩阵压缩，全连接层的计算复杂度可以由O(pqB2)减少为O(pqBlbB)。

2.2 卷积层的压缩

为方便叙述，约定M、N分别为三维卷积的输出、输入通道数，D、R、C分别为输出特征在时间、高度、宽度三个维度上的大小，K、B分别表示卷积核尺寸和循环矩阵块大小，则输入特征图I、权重W和输出特征图O分别是尺寸为N×(D+K-1)×(R+K-1)×(C+K-1)、M×N×K×K×K、M×D×R×C的多维张量。为了使用循环矩阵压缩三维卷积层权重，首先将权重张量W（图4（a））视为K3个尺寸为M×N的矩阵，如图4（b）所示，而后再将其中每个M×N矩阵划分为P×Q个尺寸为B×B的子矩阵Wp,q,i,j,k(P=M/B,Q=N/B,p=0,1,…,P-1,q=0,1,…,Q-1,i,j,k=0,1,…,K-1) ，最后，令每一个子矩阵Wp,q,i,j,k均为循环矩阵。与之相对应，原权值矩阵可由子矩阵Wp,q,i,j,k的生成向量wp,q,i,j,k表示，如图4（c）所示，从而将卷积层权值的存储开销由MNK3减少为PQBK3，取得B倍的压缩效果。

图4 卷积层权重的压缩Fig.4 Compression of convolutional layer weights

与卷积层的压缩过程相对应，其计算过程如图5所示，其中①是原始的三维卷积的伪代码。由于在压缩卷积层权重时已经对输入、输出通道进行了分块操作，因此，①可以进一步改写为图5 中②所对应的分块矩阵-向量乘法的形式。进一步地，根据卷积层的压缩策略，对于每一组给定的p,q,i,j,k,W[pB+B:pB][qB+B:qB][i][j][k]均为循环矩阵，因此②可以进一步通过③所对应的FFT 操作进行优化，其中，w[p][q][:][i][j][k]是循环矩阵W[pB+B:pB][qB+B:qB][i][j][k]对应的生成向量。

图5 卷积计算的加速Fig.5 Acceleration of convolutional calculations

得益于三维卷积中多种形式的数据复用，FFT加速给卷积层带来的收益更加可观。压缩前卷积层的计算复杂度为O(MNDRCK3)，而根据对图5中③的分析可知，对输入特征、权重以及输出特征进行FFT/IFFT变换的计算复杂度分别为O(NDRClbB)、O(K3PQBlbB)和O(MDRClbB),元素级乘法的计算复杂度为O(MNDRCK3/B),故计算复杂度的理论压缩比可以由公式（6）所描述：

考虑到在3D-CNN中，M、N、D、R、C的值远大于B、K，因此压缩后卷积层的计算复杂度（即公式（6）中的分母）可近似为O(MNDRCK3/B)，对应计算压缩比约为O(B)，相比全连接层O(B/lbB)倍的压缩效果，取得了更为明显的提升。

2.3 全频域计算

根据上述分析可知，采用分块循环矩阵和FFT 对3D-CNN的卷积层和全连接层进行压缩和加速后，网络层的计算流程变为：FFT →元素级乘法→IFFT。该过程涉及较为频繁的时域/频域切换：如图6（a）所示，由于传统前馈过程中激活、批归一化以及池化层需要在时域中进行计算，因此，每次在频域中计算完卷积层/全连接层后需要通过IFFT将结果转化至时域（图6（a）中的①）。而在进行下一次卷积层或全连接层操作时，又必须将时域特征通过FFT转换至频域（图6（a）中的②）。频繁的频域/时域转换将严重影响前馈过程的硬件加速效果：（1）由于FFT/IFFT是计算密集型算法，转换过程本身存在较大开销；（2）在设计硬件加速器时，需要专门的硬件模块计算FFT/IFFT，会消耗额外的硬件资源；（3）FFT/IFFT算法会引入计算误差，对模型量化不友好。

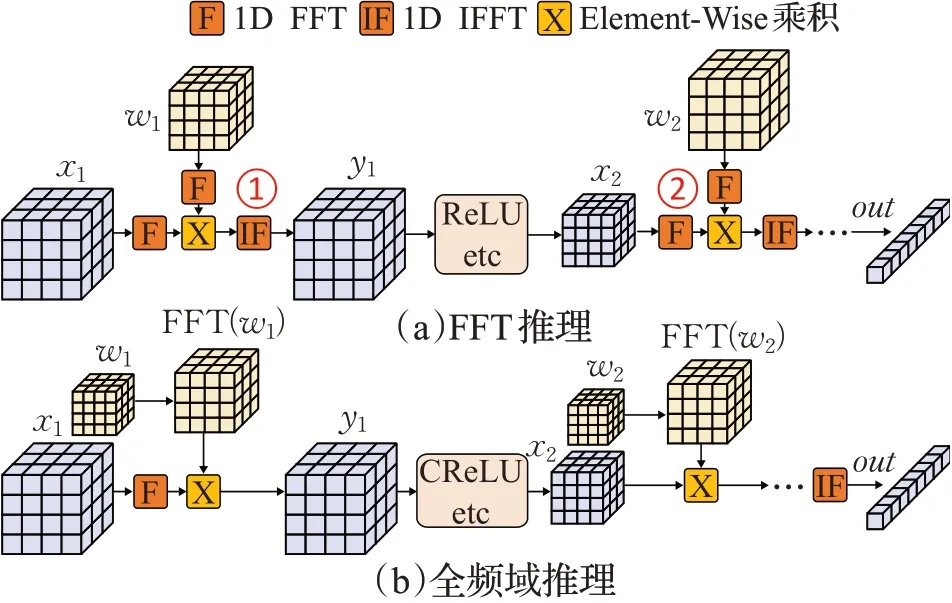
图6 全频域推理Fig.6 Full frequency domain inference

为解决该问题，本文提出了针对激活层、批归一化层、池化层的频域算子，并在此基础上实现了全频域前馈计算，以此消除频繁的时域/频域切换开销。全频域前馈过程如图6（b）所示。在选取频域算子时综合考虑了以下两方面因素：其一是频域算子的计算复杂度不能过高，否则其计算开销可能抵消全频域计算所带来的收益；其二是频域算子的引入不能造成较大的精度损失。权衡这两点，本文最终选择CReLU[24]、CBN和CMaxPool作为激活层、批归一化层、池化层的频域算子，相应表达式分别如公式（7）~（9）所示：

其中，ReLU、BN和Maxpool分别是实数域上的激活、批归一化和最大池化操作。由公式（7）~（9）可知，CReLU、CBN 和CMaxpool 相当于对数据的实部和虚部分别进行ReLU、BN 和Maxpool 操作，因此，其计算开销较小。为进一步探究频域算子对模型精度的影响，本文使用C3D 网络模型和UCF101 数据集对所提出的频域算子进行了消融测试，结果如表1 所示。从表中可以看出，引入CReLU 后造成了0.37 个百分点的精度损失，而CBN、CMaxpool 的引入分别带来0.556 个百分点和0.417 个百分点的精度提升。由此可见，所选频域算子CReLU、CBN和CMaxpool在具有较低计算复杂度的同时，能够较好地保持模型精度，充分符合全频域前馈过程的处理要求。

表1 C3D上频域算子消融实验Table 1 Frequency domain operator ablation experiment on C3D

2.4 复数域内的模型量化

为了进一步降低模型尺寸和硬件部署时的开销，本文对压缩后的3D-CNN 进行了量化操作。与全频域内的前馈过程相对应，本文的量化操作是在复数域上进行的。在传统INT8 量化感知训练方法的基础上[25]，本文进一步提出了以下量化方案：

其中，zr、zi分别为复数z的实部和虚部；Quant 为实数域上的对称量化算子，Quant(x)=clamp([x/s],-127,127),clamp(x,a,b)用于将x的值约束在a、b之间，若x小于a则返回a，若x大于b则返回b，否则返回x,s为伸缩因子，[⋅]为取整操作；Dequant 为实数域上的反对称量化算子，Dequant(x)=x⋅s。将CQuant和CDequant算子构成的伪量化算子插入到神经网络的计算图中，即可实现量化感知训练[25]。在量化过程中，为了降低量化对模型精度的影响，权重和激活、实部和虚部均采用独立的伸缩因子。其中，权重实部和虚部的伸缩因子Siw（i=1，2，分别表示实部和虚部，下同）均是基于权重wi的统计信息在训练过程中动态计算得到的，如公式（12）所示：

而为了平滑激活的伸缩因子，防止其在训练过程中出现剧烈抖动，本文采用滑动平均法（exponential moving average）更新，如公式（13）所示：

在上式中，β∈[0,1]，起调节作用，其值越小，说明历史值的影响越大，反之则当前值(max(|ai|)/127 占据主导地位。此外，在反向传播过程中，由于取整函数（round）是不可导的，因此，本文采用直通估计器（straightthrough estimator，STE）[26]估计其导数，如公式（14）所示：

3 硬件设计与优化

3.1 加速器的硬件架构

加速器的整体架构如图7 所示，主要包括控制单元、AXI DMA、输入特征缓存、权重缓存、输出特征缓存、计算单元（PEs）以及后处理单元。由于FPGA片上存储资源有限，无法一次性容纳特征图和权重，因此，在设计加速器时，本文进行了循环分块优化。为了方便说明，约定Tn、Tm分别为加速器输入、输出通道的分块大小，同时也是加速器在输入、输出通道维度的并行度，Td、Tr、Tc分别为输出特征图时间、高度、宽度维度的分块大小，B为分块循环矩阵压缩时的块大小。上述硬件参数在加速器设计时可以根据模型定制化，以尽可能提升加速器的性能。在整个硬件架构中，最核心的是计算单元（PEs），如图7 所示，计算单元包含多个PE，每个PE 均由Tn/B个并行的复数乘法器构成，相乘的结果，通过一个Tn/B输入的复数加法树求和，若仅在输入、输出通道进行循环展开，则共有Tm/B×B=Tm个PE。此外，计算单元可以根据硬件资源的数量以及实际应用场景的需求进行灵活缩放，例如可以通过调节Tm、Tn的大小或者在其余维度上进行类似的循环展开来缩放加速器的并行度。因此，计算单元具有良好的可扩展性。为了给计算单元提供相匹配的片上访存带宽，输入特征缓存、输出特征缓存以及权重缓存分别由Tn、Tm、Tn×Tm/B个Bank构成，不同通道的数据存储在不同的Bank中，从而可以实现对数据的并行读写。后处理单元包括CReLU、CBN、量化和CMaxpool单元，分别如图7 ①~④所示。所有的处理单元均由两路构成，分别处理输入的实部(zr)和虚部(zi)。其中，CReLU 单元通过和实数0进行比较实现对复数实部和虚部的ReLU操作；CBN单元接受参数γ和β，并分别对输入的实部和虚部进行线性变换；量化单元首先对输入的实部和虚部分别进行缩放(×1/s)，然后就近取整并将值限制在区间[-127,127]内；CMaxpool单元由两路比较树构成，并由此求得每一路池化窗口内所有数据的最大值。AXI DMA 用于在片外存储器和加速器之间搬运数据。控制单元负责控制与调度整个加速器的工作。为了掩盖数据的传输时间，本文的硬件加速器还进行了双缓冲操作，通过在加载、计算、写回之间实现粗粒度流水，进一步增大加速器的吞吐率。

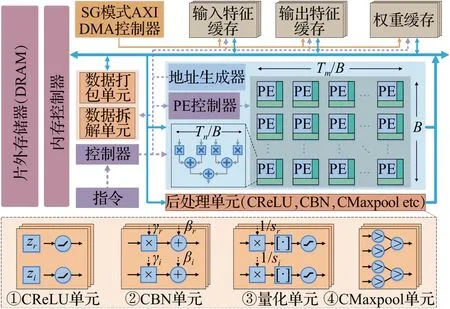
图7 加速器硬件架构Fig.7 Hardware architecture of accelerator

3.2 高效的数据排布策略

为增大片外访存效率，充分利用片外存储器带宽，本文对特征图进行了数据重排。需要强调的是，由于加速器的计算单元是在特征图的通道维度并行的，因此，相应的缓存单元也需要在通道维度分割，以提供足够的片上带宽。例如，在图8 ③中，片上缓存被分割为4 个Bank，每个Bank负责存储一个通道的特征图，以支持计算单元并行的需求。

图8 NCHW和NC/xHWx数据排布(x=4)Fig.8 NCHW and NC/xHWx data arrangement(x=4)

现以二维特征图为例（三维类似），阐述本文的数据排布策略。如图8所示，左侧是一个8通道的特征图，每一幅特征图的大小均为2×2，图8 ①是常见的NCHW数据排布格式，该格式按照行主序的方式，先排布通道0的特征图，接着排布下一个通道的数据。然而，在这种数据排布方式下，片外访存效率难以被充分利用：假设数据位宽为8 位，总线位宽为32 位，则理论上该总线可以在1个周期内读取4个数据。然而，在NCHW数据排布下，即使总线能够在一个周期内读取4 个数据（例如图8 ①红框所示），由于所读取数据属于同一通道，因此无法在同一周期内写入片上缓存，从而造成停顿。为此，本文采用了图8 ②所示的NC/xHWx 数据排布格式（以x=4 为例，即NC/4HW4），该格式首先排布前4 个通道（0~3）的特征图，具体的排布策略为：将这0~3通道同一像素位置（1）的数据取出并排列，接着取出这4 个通道下一个像素位置（2）的数据排列，直至所有数据都排列完毕，再对4~7 通道进行类似的排布。在该排布下，总线可以一次并行读取4个分布于不同通道的数据（例如图8 ②中红框所示），并能够在同一周期内将所读数据写入片上缓存，从而充分利用了片外访存带宽。

3.3 针对复数运算特点的设计优化

3.3.1 基于复数共轭对称性的优化

由于在3D-CNN中，时域的激活、权重均为实数，因此，其经过FFT 变换后得到的频域激活、权重满足共轭对称性。本文利用该性质，进一步对加速器进行了优化：一个长为N的实数序列x经过FFT变换后，得到的复数序列X满足共轭对称性，如公式（15）、（16）所示：

其中，Imz表示取复数z的虚部，*表示复数的共轭，即(a+bi)*=a-bi。因此，在对频域的权重（可以预先转化到频域）和激活进行存储时，可以只存储其一部分值。对于偶数的N来说（本文在选择循环矩阵分块大小时，均采用偶数），只需存储X0,X1,…,XN/2共N/2+1 个复数，考虑到X0和XN/2均为实数，因此，可以将X0和XN/2进一步打包为一个复数X0+iXN/2，从而将存储空间减半，如图9 所示。此外，由于共轭复数的乘积等于复数乘积的共轭，如公式（17）所示：

图9 基于复数共轭对称性的优化Fig.9 Optimization based on complex conjugate symmetry

因此，在频域进行复数向量的元素级乘法时，可以只计算前N/2+1 项的乘积，而后N/2-1 项乘积的结果可以由前者的复共轭得到，从而减少约50%的计算量，如图9所示。

3.3.2 复数乘法优化

由于在2.3节中，通过引入频域算子，实现了全频域推理，因此，在本文中，复数乘法是加速器设计中最核心的运算。然而，和实数乘法相比，复数的乘法更加复杂，如公式（18）所示：

上式表明，1次复数乘法包含了4次实数乘法和2次实数加法。为了进一步减少其计算量，作如下变换：

由式（19）~（22）可知，经过优化后，原先4次实数乘法、2次实数加法的复数乘法运算，计算量可以减少为3次实数乘法和5 次实数加法。由于加法的计算复杂度远低于乘法，因此，上述优化可以有效降低复数乘法的计算复杂度，进而减少硬件资源（如DSP Slice）的消耗（接近25%），提升加速器的计算效率。

3.3.3 基于数据共享的计算资源优化

DSP 是FPGA 中重要的计算资源，以Xilinx FPGA为例，在UltraScale/UltraScale+系列的FPGA中，DSP48E2 Slice 包括1 个27×18 bit 的乘法器和1 个48 bit 的加法器，由于其支持较大的位宽，因此，在数据位宽较小且存在数据共享的情况下，可以进一步优化从而提高DSP的利用率[27]。与此同时，在3D-CNN 中，存在着丰富的数据复用，包括输入特征图复用（input feature map reuse）、卷积核复用（filter reuse）以及卷积复用（convolutional reuse），这些复用使得数据共享成为可能。基于以上两点，本文提出了基于INT9乘法的DSP优化方法。

现考虑有三个复数x=a+bi,w1=x1+iy1,w2=x2+iy2，需要计算o1=x×w1和o2=x×w2，结合3.3.2 小节中复数乘法的优化，对于i=1，2，有：

注意到，A1和A2共享了乘数a+b,B1和B2共享了乘数b,C1和C2共享了乘数b-a，在本文INT8 量化的情况下，a+b、b-a、x1+y1以及x2+y2都需要用9位有符号整数表示，因此，可以进一步将问题抽象为：a、b、c均为INT9 类型，需要计算x=a×b,y=a×c，如何对其进行优化可以减少DSP资源消耗。

如图10所示，为了对x、y的计算进行优化，首先将b左移18位，同时将c符号扩展为27位，两者求和，然后再和a相乘，得到o=a×(b<<18+c)，最后，再从o中将x和y拆分出来：x=o35:18+o17,y=o17:0。通过上述优化，可以实现1个DSP48E2 Slice同时计算两个INT9乘法的目的，这充分挖掘了Xilinx DSP48E2 Slice 的计算能力，显著降低了DSP 资源的使用量，进而提升了加速器的计算效率。

图10 INT9乘法DSP优化Fig.10 DSP optimization of INT9 multiplication

4 实验评估

4.1 实验设置

为了对本文提出的方法进行评估，本文选择了两个典型的3D-CNN模型：C3D[2]和3D ResNet-18[6]。C3D具有非常规整的网络结构，它包含8 个卷积层、5 个池化层、2个全连接层以及一个Softmax层。其中，所有卷积核的大小均为3×3×3，步长均为1×1×1，所有的最大池化层，除第一个池化核的尺寸和步长为1×2×2 外，其余均为2×2×2。3D ResNet-18由2D ResNet-18演化而来，因此，在3D ResNet-18中，不仅包含3×3×3的标准卷积，还包含1×1×1的点态（point-wise）卷积。此外，3D ResNet-18还具有残差连接结构，用以解决深度网络梯度消失和梯度爆炸的问题。本文采用的数据集是UCF101，该数据集包含101个类别共13 320个视频，分辨率为320×240，帧率不固定，一般为25帧或29帧。

本文基于Pytorch深度学习框架实现对模型的压缩和训练，实验采用的GPU 配置为4 块NVIDIA TITAN X。在训练过程中，神经网络模型所有的ReLU、BN 及Maxpool操作均被替换为CReLU、CBN和CMaxpool，以实现全频域推理。同时，本文还在复数域上进行了INT8 量化感知训练。在整个训练过程中，相同模型的训练参数是一致的：输入视频的空间尺寸为112×112，通道数为3，共16帧，学习率为0.01，采用余弦学习率更新策略，训练300 个Epoch，C3D 和3D ResNet-18 的批处理大小分别为64和128。本文选择Xilinx ZCU102 FPGA作为实验的硬件平台，开发工具为Xilinx Vivado HLS 2019.2，本文分别为C3D 和3D ResNet-18 设计了相应的硬件加速器。其中，C3D 加速器的硬件参数为(Tn,Tm,Td,Tr,Tc)=(32,64,2,7,7)，并对Tn、Tm进行循环展开；3D ResNet-18 加速器由两个硬件加速核构成，分别用于加速1×1×1和3×3×3卷积，其硬件参数分别为(Tn,Tm,Td,Tr,Tc)=(8,32,2,7,7)和(Tn,Tm,Td,Tr,Tc)=(32,32,2,7,7)，前者对Tn、Tm进行循环展开，后者对Td、Tn、Tm进行循环展开。此外，为了提高片外访存效率，本文对特征图进行了NC/8DHW8 格式的数据排布。由于加速器和片外存储器是通过AXI 总线传输数据的，因此，为了适配NC/8DHW8 数据排布格式，AXI总线接口的位宽被设置为128，每次可以并行地读取8个复数（每个复数的实部和虚部均为8位，共16位）。本文使用Xilinx Vivado 2019.2 对设计完成的加速器进行综合、布局布线、生成比特流，加速器的时钟频率为200 MHz。

4.2 实验结果

4.2.1 模型精度与压缩比

为了探究模型精度和压缩比之间的关系，取块大小为1（即未压缩的模型）、4、8、16在C3D和3D ResNet-18上进行了实验，结果如图11所示。由图可知，当分块大小为4 时，C3D 和3D ResNet-18 的精度损失仅为0.278和0.51 个百分点，相应的存储与计算压缩比为16 倍和2.67倍。作为对比，文献[13]对C3D进行以块为单位的剪枝，以0.34个百分点的精度损失为代价获得了1.05倍的参数压缩比和3.18 倍的计算压缩比。显然，3D FCirCNN以更小的精度损失（0.278个百分点）取得了更加显著的参数压缩效果。而在计算量压缩方面，尽管3D FCirCNN 取得的压缩效果相较文献[13]减少了约16%，但3D FCirCNN 对C3D 的压缩是高度规则的，因此在实际部署时可以取得更优的效果，这一点在4.2.2小节3D FCirCNN 和其他相关工作的比较中得到了充分体现。当分块大小为16 时，C3D 和3D ResNet-18 的精度损失分别为2.825和3.196个百分点，压缩对精度造成了较大影响。因此，为了在精度和压缩比之间取得较优权衡，本文最终采用块大小为8的分块循环矩阵来压缩C3D 和3D ResNet-18，相应的存储与计算压缩比分别为32 倍和5.33 倍，精度损失分别为1.25 和1.71 个百分点。相比之下，3D VNPU[14]采用Winograd算法和INT8量化，以1 个百分点的精度损失为代价获得了4 倍的存储压缩比和3.33倍的计算压缩比。通过分析不难发现，3D FCirCNN 在精度损失稍大的情况下（0.25 个百分点），在3D VNPU 的基础上将存储和计算的压缩比进一步提升了8倍和1.6倍，从而充分说明了3D FCirCNN在3D-CNN模型压缩方面的优越性。

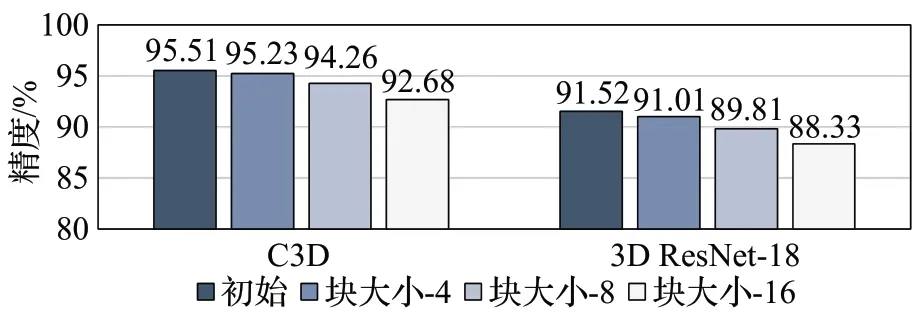
图11 压缩比对精度的影响Fig.11 Effect of compression ratio on accuracy

4.2.2 和相关工作的比较

表2列出了针对两个不同模型所设计的加速器的资源消耗情况。表3 给出了加速器和其他相关工作的比较结果。由表3可知，得益于本文算法压缩和硬件加速的协同优化，C3D 和3D ResNet-18 加速器的吞吐量分别达到了2 692.81 GOP/s 和1 591.52 GOP/s，相较于表中其余工作的加速比分别为1.99~16.68 倍和1.18~9.86 倍，取得了显著提升。此外，由于本文所采取的针对复数乘法的DSP优化技术，C3D和3D ResNet-18加速器分别取得了每DSP 3.349 GOP/s 和1.677 GOP/s 的吞吐率，相较于表2 中其余加速器的结果分别提升了2.54~16.18 倍和1.27~8.1 倍。因此，本文所提出的方法可以以较少的硬件资源为代价，取得优异的性能，这一点在硬件资源、功耗受限的嵌入式平台上显得尤为重要。

表2 加速器资源消耗Table 2 Resource utilization of accelerator

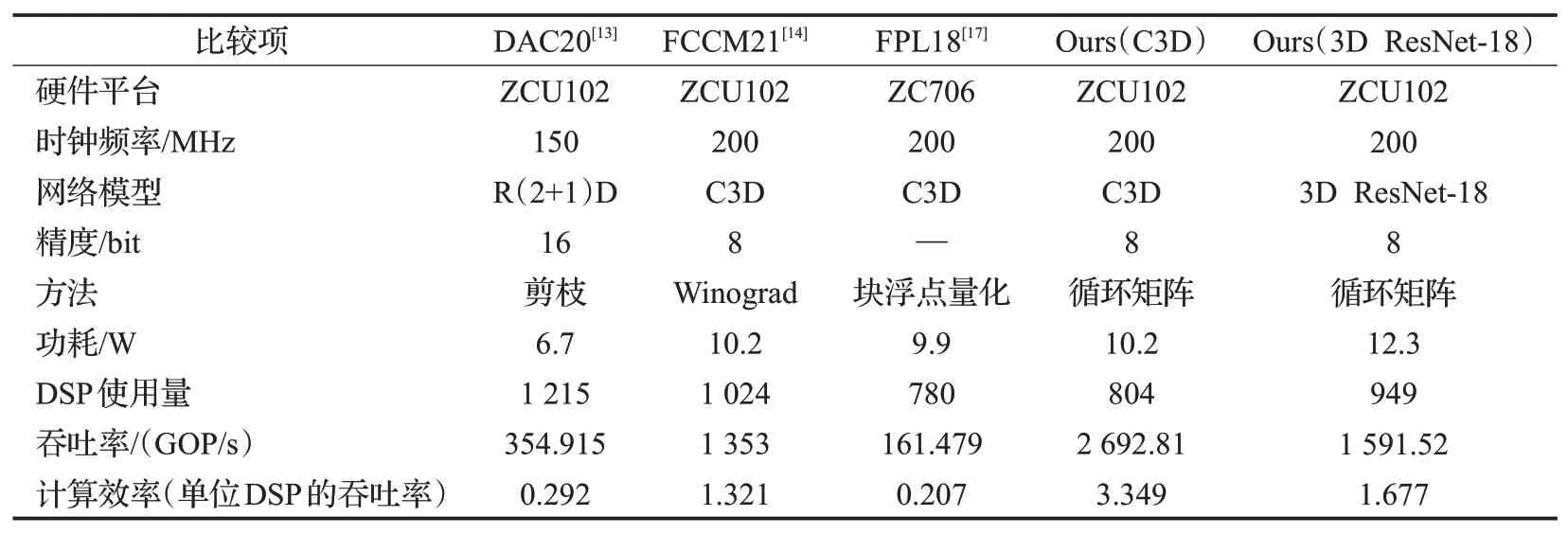
表3 和先前实现的比较Table 3 Comparison with previous implementations

5 结束语

本文提出了3D FCirCNN，一个算法-硬件协同设计与优化的方法来对3D-CNN进行加速。在算法层面，本文采用基于分块循环矩阵的压缩方法，并进一步利用FFT加速计算。此外，为了消除由于FFT带来的频繁的时域/频域切换开销，本文引入了频域内的激活、池化和批归一化层，实现了全频域计算。本文还采用与分块循环矩阵正交的INT8对称量化对3D-CNN进行进一步压缩。在硬件层面，本文为压缩后的3D-CNN设计了一个专用的硬件架构，并针对硬件资源、存储带宽进行了一系列优化。在精度损失可以接受的范围内，3D FCirCNN带来了接近32 倍的压缩效果，相较于以往最先进的工作，本文的加速器在Xilinx ZCU102 FPGA平台上取得了多达16.68倍的性能提升和16.18倍的计算效率提升。