基于贝叶斯超参数优化的Gradient Boosting方法的导弹气动特性预测

崔榕峰 马海 郭承鹏 李鸿岩 刘哲

摘 要：在导弹设计与研发的初期阶段，需要寻求高效且低成本的导弹气动力特性的分析方法。然而，气动性能分析过程中往往存在试验成本高、周期长、局限性大等问题。因此，本文采用基于提升（Boosting）的机器学习集成算法进行导弹气动特性预测，通过输入导弹的气动外形参数、马赫数和迎角，对于导弹气动力系数实现快速预测。结果表明，Boosting能够对导弹气动力系数进行精准高效预测。为进一步提升预测精度，与传统的机器学习参数调整方法相比，采用贝叶斯优化方法对梯度提升（Gradient Boosting）算法超参数进行优化，调优后的Gradient Boosting方法预测的导弹气动力系数与实际值吻合度得到提升，并将贝叶斯优化的Gradient Boosting方法与XGBoost、LightGBM、Adaboost方法进行了对比，贝叶斯优化的Gradient Boosting方法预测精度优于其他Boosting方法，证明了优化方法的可行性与有效性。

关键词：导弹； 气动特性； Boosting； Gradient Boosting； 贝叶斯优化

中图分类号：V211.3 文献标识码：A DOI：10.19452/j.issn1007-5453.2023.07.003

在导弹气动外形方案设计阶段，气动性能分析是重要的组成部分，通常会根据战术指标要求提出若干总体布局方案，并对各种方案进行评估，同时还需要开展一些参数优化，以确定几个优化方案。传统的导弹气动性能参数获取主要通过飞行试验方法、计算流体力学（CFD）方法和风洞试验方法[1-2]。飞行试验和风洞试验都存在成本高、周期长、存在局限性等问题，所以在导弹设计的初步阶段不适宜使用，而CFD方法不可避免地存在计算复杂、计算代价高等问题[3-5]。

近年来，基于机器学习方法预测分析导弹的气动特性研究取得了一些突破性进展。文献[6]提出了一种基于神经网络的思维进化算法，该方法对于导弹气动参数的预测具有明显的优化效果。文献[7]提出了一种基于自动核构造高斯过程，对某导弹气动特性快速预测具有良好的性能。文献[8]、[9]分别使用人工神经网络和卷积神经网络对导弹的气动参数及气动外形进行预测分析，试验结果也验证了其可行性。但目前提出的机器方法中，可能存在对于决策者的可解释性较差、数据预处理过于复杂、预测结果过度拟和等问题。

本文采用一种基于提升（Boosting）方法中的梯度提升（Gradient Boosting）算法进行导弹气动特性预测。近年来，Boosting方法作为机器学习中的一种集成方法被广泛应用于解决不同的分类与回归问题，并取得了突破性的进展[10]。在气动特性分析方面，与传统的物理试验、数值仿真方法相比，Boosting方法因其快速且低损耗的预测优势，能够缩减分析的时间与经济成本。同时，与其他机器学习方法相比，Boosting方法通过其决策树的特性，从根本上减少了模型过拟合等问题。从时间复杂度上来看，建立决策树需要的时间成本较低，与支持向量机或神经网络等算法相比，Boosting算法在计算时间上更具有优势[11]。

本文通过使用某模拟器软件，将某导弹几何外形与飞行条件参数作为输入，并计算其对应的气动力系数。应用基于回归树的Boosting方法来验证模型方法对于导弹气动力系数预测的可行性和有效性，并通过贝叶斯优化方法对于Boosting算法中的Gradient Boosting方法进行优化处理，并比较优化前后的效果。

1 Boosting方法

Boosting方法是一种基于集成学习的机器学习技术。集成学习算法是指通过一系列弱学习器组合成一个强学习器，从而可以达到最小化预测误差的目的。Boosting方法则以基于决策树的集成方法为核心，进行逐步增强的集成训练，通过不断建立新的决策树纠正先前决策树模型中存在的错误，直到精准预测训练数据集或者添加的决策树或回归树的数量达到了最大限度[11]。Boosting方法因描述和绘制决策树相对容易，所以其可解释性有助于决策者进行可视化和理解。除此之外，基于树的集成方法可以处理不同类型和分布的预测变量，需要很少的数据预处理，并且可以拟合复杂的非线性关系。同时，如果数据出现多重共线性的特征，不需要对数据进行特征筛选从而减少变量之间的相关性[12]，并且Boosting方法具有非参数特点，可以不假定数据遵循特定的分布，从而节约数据转换为正态分布的时间成本。另外，Boosting方法对过拟合具有鲁棒性，其应用存在高偏差的多個弱学习器，并将其组合成一个强学习器，所以从根本上减少了模型过拟合的问题[12]。

1.1 Gradient Boosting回归树方法

Gradient Boosting作为一种机器学习的算法，通过以弱学习模型不断集合的形式产生最终的强学习模型。当弱学习模型是回归树时，其被称为Gradient Boosting回归树方法。Gradient Boosting决策树方法采用构建浅层树，并且随后生成的每一棵树都在前一棵树的基础上学习和改进。虽然每组浅层树的预测效果一般，但是通过每组浅层树之间不断的梯度增强，最终形成的基于多组浅层树的组合会得出有效的预测结果[16]。

Gradient Boosting回归树算法主要分成三个步骤：（1）确定优化的损失函数并生成初始值；（2）建立单个回归树进行预测分析；（3）通过循环添加新的回归树以最小化损失函数，最终得出一个叠合模型[13]。具体步骤为：

（3）为了最终能获得最优的模型性能，对第（2）步进行K次迭代，从而将K个回归树逐步添加到组合模型中[14]。

Gradient Boosting回归树算法因以回归树作为基础估计器，具备了回归树的优点。首先，模型对于数据缺失值敏感度非常低，无须进行数据填补工作。其次，因其具有非参数化的特征，无须进行数据预处理的工作，如对于特征进行标准化或归一化处理。最后，回归树可以非常灵活地处理不同函数分布的数据。同时，回归树也具有很明显的缺点，其中最大的问题则是模型易出现过度拟合，而Gradient Boosting与回归树算法结合所产生的集成方法则解决了此类问题，这是因为Gradient Boosting回归树算法采用的都是复杂程度相对较低的回归树（弱学习器），所得到的结果方差较小，通过梯度提升生成的叠合模型很有效地解决了结果过拟合的问题[15]。

1.2 其他的Boosting方法

除Gradient Boosting回歸树算法外，基于Boosting的集成方法的算法也在其他方向有所进展。其中自适应提升（Adaboost）作为一种迭代提升的集成方法，同时被广泛应用。Adaboost与Gradient Boosting 的主要区别是基于不同的角度对上一轮迭代所产生的训练错误进行调整。Adaboost是根据当前迭代中的实际结果调整权重，目的是在下一轮的模型训练和学习中，给予训练中产生的错误数据更多关注，所以算法需要不断对数据重新加权得到最终的聚合权重[16]。

另外，作为基于Gradient Boosting的二次开发算法，极端梯度提升算法（XGBoost）和轻量级梯度提升机（LightGBM）同样展示出了高效的性能。XGBoost在损失函数上进行了二阶泰勒展开、引入了目标函数的正则项等一系列改进，在训练速度和精度上都有很大的提升[17]。而LightGBM则采用更优的leaf-wise方法分裂叶子节点，与其他用于Boosting算法中的分裂算法depth-wise或level-wise进行比较，leaf-wise可以在损失函数上降低更多且运行速度更快[18]。

2 贝叶斯优化方法

在机器学习中，超参数优化可以使模型本身发挥出最佳的性能，所以对于机器学习算法进行超参数优化是必要的。然而，由于大量的超参数和复杂的模型，如集成方法或深度神经网络方法，超参数优化在评估目标函数以找到最优解的过程中存在时间成本非常高的问题。到目前为止，网格搜索与随机搜索常被用于解决超参数选取和优化的问题[19]。其中，网格搜索是指通过一组手动指定的超参数值进行的穷举搜索法，也称暴力搜索法；而随机搜索舍弃了暴力搜索的方法，寻找网格空间来选取随机的参数组合。然而，这些方法都无法保证能获取到超参数的最优解且相对低效，通常会浪费大量时间评估比较差的超参数[20]。

与随机搜索或网格搜索相比，贝叶斯方法则拥有跟踪过去评估结果的特点，将超参数映射到目标函数形成一种概率模型，这种模型也被称为目标函数的代理模型[21]。与目标函数相比，代理模型更容易进行优化。贝叶斯方法通过选择在代理模型上表现出最佳的超参数，以此来评估实际目标函数，接下来不断更新代理模型，得出新的超参数结果，再次评估目标函数，直到达到最大的迭代次数方才停止。贝叶斯方法的主要核心是通过在每次评估目标函数后不断更新代理模型，使其获取到的数据误差最小化[22]。整体上来看，贝叶斯优化方法是有效的，其使用更多的时间在代理函数中选择超参数，以减少对目标函数的调用，并且通过评估过去结果中性能更好的超参数，可以在更少的迭代中找到比随机搜索和网格搜索更优的模型超参数设置。

综上所述，假设F为目标函数，S为超参数的搜索范围、 s为选择的超参数组合、K为采集函数、P为代理模型，Data表示采样的数据集、 j为最大迭代次数，贝叶斯优化的伪代码流程可以表示为

3 试验流程与结果分析

3.1 数据集生成

本文采用某软件对于输入的某导弹参数与气动参数进行升力、阻力系数生成，生成的导弹几何外形如图1所示，本文涉及的导弹几何参数有弹翼轴向位置、弹翼展长、弹翼根弦长、十字舵展长、十字舵根弦长、十字舵梢弦长，气动参数有马赫数、迎角。每种导弹参数在±10%的取值范围内波动，并通过随机生成的方式形成导弹参数数据。每组导弹几何参数（共6个）在不同的来流工况 Ma = {0.5， 0.8， 1.2， 2.5， 3.5}、α = {0， 4.0， 8.0， 12.0， 16.0， 20.0， 24.0， 28.0} 组合下，共生成40个对应的气动力系数。本文如上所述共产生185组不同的导弹几何构型，共生成7400个气动力系数。

3.2 试验流程介绍

本文的试验流程主要分为两个部分：第一部分为论证Boosting方法对于导弹气动力系数预测的可行性和有效性，其中涉及的Boosting方法有：Gradient Boosting、XGBoost、LightGBM和Adaboost方法。第二部分是对Gradient Boosting方法进行贝叶斯优化，比较优化前后的精准度与拟和度的差异变化。试验使用交叉检验方法将部分训练集作为检验集进行结果验证，训练集与测试集的比例为8∶2。本文提出的Boosting和贝叶斯优化算法均基于Python 3.10开发环境开展，其中Gradient Boosting和Adaboost方法使用的是sklearn工具包，XGBoost和LightGBM分别使用的是xgboost和lightgbm工具包。

在贝叶斯优化中，对XGBoost和LightGBM进行初步优化测试，其效果并不理想，优化后的结果的精准度无法超过其默认设置。而Adaboost方法本身参数很少，优化方法并不适用，最终选择Gradient Boosting方法进行贝叶斯优化。优化下的Gradient Boosting参数选取中，本次试验选择了learning_rate、n_estimators、min_samples_split和max_depth共4种参数。其中，learning_rate表示学习率，其控制着每个回归树的贡献度，本次试验学习率的取值范围为0.1～1；n_estimators表示最终聚合模型的回归树数量，本次试验学习率的取值范围为50～500；min_samples_split表示拆分每个回归树中内部节点所需的最小样本数，本次试验设计的取值范围为2～5；max_depth表示每个回归树的最大深度，其控制着树中的节点数，本次试验设计的取值范围为1～5。试验共进行100次迭代，通过贝叶斯优化算法选取出在取值范围内最优的超参数组合。

3.3 試验结果分析

从表1中Boosting方法预测升力系数的比较结果可知，如果暂时不计入Gradient Boosting优化后的结果，XGBoost和LightGBM的预测结果精准度良好，其次是Gradient Boosting，其精准度的结果与前两者相比略显下降，最后是Adaboost，与其他三种方法相比，其各项指标有所不足。总体来看，在Gradient Boosting方法优化前，XGBoost与LightGBM对于导弹升力系数的预测效果显著。

通过对Gradient Boosting进行贝叶斯优化，最终优化选取的参数组合为（learning_rate = 0.19838，max_depth = 4，n_estimators = 499，min_samples_split = 4）。从表1中结果来看，Gradient Boosting模型方法与优化前相比，在精准度上有所提高，这说明贝叶斯优化方法对于Gradient Boosting的性能提升有所帮助。同时通过对比发现，优化后的Gradient Boosting在精准度上均优于其他Boosting方法，可见其优化效果是可观的。

从表2中Boosting方法预测阻力系数的比较结果能够得出与表1中相同的结论。对于阻力系数，贝叶斯优化下的Gradient Boosting最终选取的参数组合为（learning_rate= 0.09276，max_depth=4，n_estimators=475，min_samples_split =3），Gradient Boosting采用优化得出的超参数组合后，与其他Boosting方法相比，对阻力系数的预测在精准度方面展现出了最佳的性能。最后，通过对表1和表2进行比较得出，Boosting方法对于阻力系数预测结果的精准度与其升力系数相比，阻力系数的精准度结果略好一些。

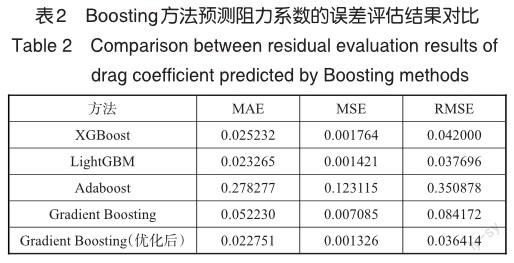
图2与图3分别展示出了Gradient Boosting优化前后对于升力和阻力系数的预测拟和结果，图中黑色虚线代表的是对角线，越靠近对角线的点，说明拟和程度越好。从图2中能够得出，无论是升力还是阻力系数分析，均可以观察到模型优化后拟和度有所提升。这可以说明贝叶斯优化方法对于Gradient Boosting方法的优化效果是显著的。

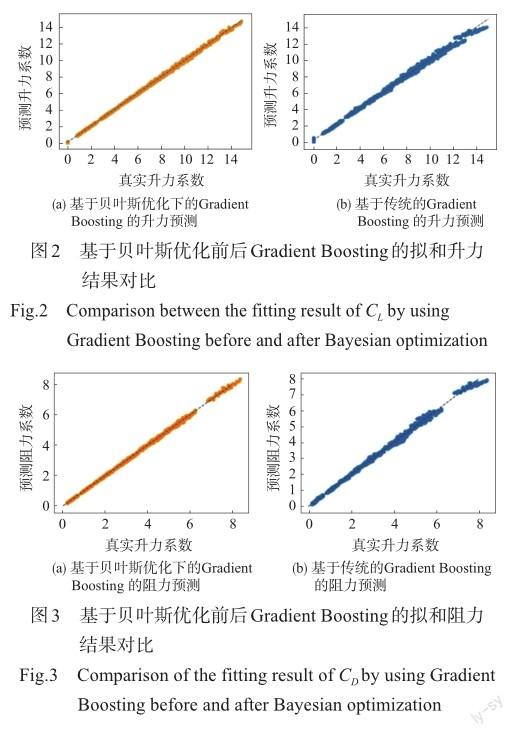
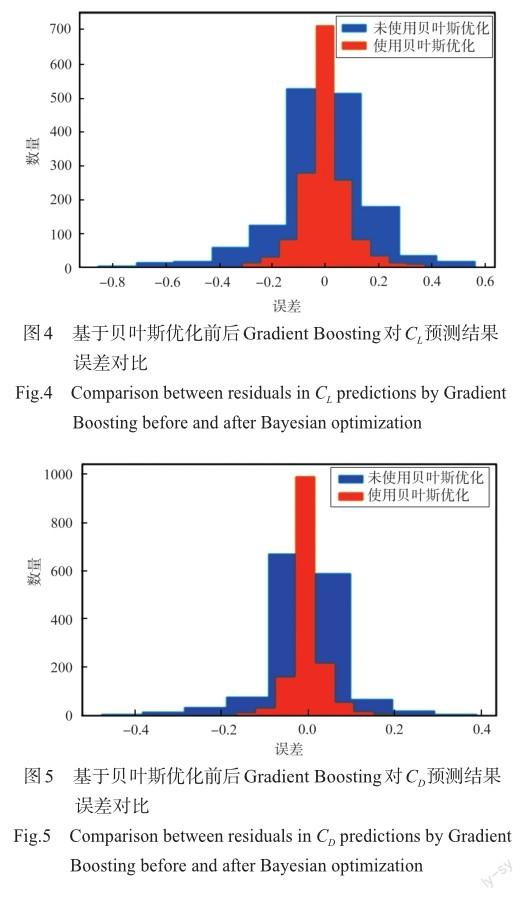
图4和图5分别展示了在贝叶斯优化方法前后，Gradient Boosting方法对于升力系数CL和阻力系数CD的预测结果的误差直方图，从图中可以看出，无论是对于CL还是CD，贝叶斯优化与Gradient Boosting方法结合后使误差的范围明显缩小，其误差结果更加趋近于零。另外，通过观察优化前后的误差分布情况，贝叶斯优化前后的误差都近似于正态分布，这说明贝叶斯优化与Gradient Boosting方法对于CL与CD的预测结果是有效的。

4 结论

针对风洞试验方法和CFD方法对于导弹的气动力特性分析存在很多局限性问题，本文采用基于机器学习中多种Boosting集成学习算法与贝叶斯优化方法对导弹气动数据进行预测分析，得到的结论如下：

（1）通过比较Boosting方法中Gradient Boosting、XGBoost、LightGBM和Adaboost方法，试验结果表明XGBoost和LightGBM有着良好的准确度。同时， Gradient Boosting在未优化前的性能虽略差于前两者，但也表现出了较高的精准度和拟和程度。

（2）基于贝叶斯优化下的Gradient Boosting方法与其他Boosting方法相比，可以得出采用贝叶斯优化的Gradient Boosting方法表现出了最佳的性能，不仅在精准度上达到最优，而且拟合度也发生显著的提升。这说明贝叶斯优化方法对于模型性能的提升是有效的。

（3）目前数据集中考虑到的几何参数有限，后续计划增加构型的数量进一步增加样本总量与样本维度，探究Gradient Boosting贝叶斯优化算法的极限适用范围，并进行贝叶斯优化算法中高斯过程的算法改进，从而提升预测的精准度。

参考文献

[1]Sun J， Cummings R M. Evaluation of missile aerodynamic characteristics using rapid prediction techniques[J]. Journal of Spacecraft and Rockets， 1984， 21（6）： 513-520.

[2]吕国鑫.飞航导弹气动设计[M].北京：中国宇航出版社，1989. Lyu Guoxin. Aerodynamic design of cruise missile [M]. Beijing： China Aerospace Press， 1989.（in Chinese）

[3]Yue Chunguo， Chang Xinlong， Zhang Youhong， et al. Numerical calculation of a missile’s aerodynamic characteristic[J]. Advanced Materials Research， 2011， 186： 220-224.

[4]Zhang Jian， Yang Lin， Zhang Wei， et al. Numerical simulation and experimental study for aerodynamic characteristics and powder transport behavior of novel nozzle[J]. Optics and Lasers in Engineering， 2020， 126： 105873.

[5]丘淦興. 利用飞行试验数据校验导弹气动参数[J]. 航天控制，1997（2） ： 1-5. Qiu Ganxing. Verification of aerodynamic parameters of missile using flight test data [J]. Aerospace Control， 1997（2） ： 1-5. （in Chinese）

[6]原智杰，张公平，崔茅，等.基于神经网络的导弹气动参数预测[J].航空兵器，2020，27（5）：28-32. Yuan Zhijie， Zhang Gongping， Cui Mao， et al. Prediction of missile aerodynamic parameters based on neural network [J]. Aviation Weapons， 2020， 27 （5）： 28-32.（in Chinese）

[7]胡伟杰，黄增辉，刘学军，等.基于自动核构造高斯过程的导弹气动性能预测[J].航空学报，2021，42（4）：289-302. Hu Weijie， Huang Zenghui， Liu Xuejun， et al. Prediction of aerodynamic performance of missiles based on automatic kernel construction Gaussian process [J]. Journal of Aeronautics， 2021，42（4）： 289-302. （in Chinese）

[8]Balla K， Sevilla R， Hassan O， et al. An application of neural networks to the prediction of aerodynamic coefficients of aerofoils and wings[J]. Applied Mathematical Modelling， 2021， 96： 456-479.

[9]Zan Bowen， Han Zhonghua， Xu Chenzhou， et al. Highdimensional aerodynamic data modeling using machine learning method based on convolutional neural network [J]. Advances in Aerodynamics， 2022， 4（1）： 1-31.

[10]Duffy N， Helmbold D. Boosting methods for regression[J]. Machine Learning， 2002， 47： 153-200.

[11]Elith J， Leathwick J， Hastie T. A working guide. to boosted regression trees[J]. Journal of Animal Ecology， 2008， 77（4）： 802-813.

[12]Zhang Y， Haghani A. A gradient boosting method to improve travel time prediction[J]. Transportation Research Part C： Emerging Technologies， 2015， 58： 308-324.

[13]Bentéjac C， Cs？rg？ A， Martínez-Mu？oz G. A comparative analysis of gradient boosting algorithms[J]. Artificial Intelligence Review， 2021， 54（3）： 1937-1967.

[14]Natekin A， Knoll A. Gradient boosting machines， a tutorial[J]. Frontiers in Neurorobotics， 2013， 7： 21.

[15]Bentéjac C， Cs？rg？ A， Martínez-Mu？oz G. A comparative anal‐ysis of gradient boosting algorithms[J]. Artificial Intelligence Review， 2021， 54： 1937-1967.

[16]Schapire R E. Explaining adaboost[M]. Berlin： Springer， 2013.

[17]Chen T， Guestrin C. Xgboost： A scalable tree boosting system[C]//Proceedings of the 22nd Acmsigkdd International Confer‐ence on Knowledge Discovery and Data Mining， 2016： 785-794.

[18]Ke G， Meng Q， Finley T， et al. Lightgbm： A highly efficient gradient boosting decision tree[J]. Advances in Neural Information Processing Systems， 2017， 30： 1-3.

[19]Buslim N， Rahmatullah I L， Setyawan B A， et al. Comparing Bitcoin’s prediction model using GRU， RNN， and LSTM by hyperparameter optimization grid search and random search[C].9th International Conference on Cyber and IT Service Management （CITSM）， 2021： 1-6.

[20]Victoria A H， Maragatham G. Automatic tuning of hyperparameters using Bayesian optimization[J]. Evolving Systems， 2021， 12（1）： 217-223.

[21]Snoek J， Larochelle H， Adams R P. Practical bayesian optimization of machine learning algorithms[J]. Advances in Neural Information Processing Systems， 2012， 25： 1-3.

[22]Pelikan M， Goldberg D E， Cantú-Paz E. BOA： The Bayesian optimization algorithm[C]//Proceedings of the Genetic and Evolutionary Computation Conference，1999.

[23]Ozaki Y， Tanigaki Y， Watanabe S， et al. Multiobjective treestructured parzen estimator for computationally expensive optimization problems[C]//Proceedings of the 2020 Genetic and Evolutionary Computation Conference， 2020： 533-541.

[24]Nguyen H P， Liu J， Zio E. A long-term prediction approach based on long short-term memory neural networks with automatic parameter optimization by Tree-structured Parzen Estimator and applied to time-series data of NPP steam generators[J]. Applied Soft Computing， 2020， 89： 106116.

Prediction of Missile Aerodynamic Data Based on Gradient Boosting under Bayesian Hyperparametric Optimization

Cui Rongfeng， Ma Hai， Guo Chengpeng， Li Hongyan， Liu Zhe

Aviation Key Laboratory of Science and Technology on Aerodynamics of High Speed and High Reynolds Number，AVIC Aerodynamics Research Institute， Shenyang 110034， China

Abstract： In the initial stage of missile design， the aerodynamic characteristics of missiles need to be quickly and preliminarily evaluated. When analyzing the aerodynamic performance of missiles， the traditional engineering method has the problem of high experiment costs and the long experiment period. Meanwhile， the CFD method is also difficult to calculate due to its complex calculation process， and the calculation cost is high. Therefore， this paper applys the method of missile aerodynamic data prediction based on several Boosting methods in machine learning. By inputting aerodynamic shape， mach number， and angle of attack data of the missile， the lift coefficient and drag coefficient are quickly predicted. The result shows that Boosting method can predict the aerodynamic coefficients of missiles accurately. In order to further improve the prediction accuracy， compared with other traditional hyperatameter selection methods， Bayesian Hyperparameter Optimization method as an automatic hyperatameter selection method is used to optimize the parameters of the Gradient Boosting algorithm， and it turns out that the predicted value is much closer to the actual value. Finally， the Gradient Boosting method under Bayesian Optimization is compared with XGBoost， LightGBM and Adaboost methods， and the Gradient Boosting method under Bayesian Optimization is more accurate than other Boosting methods， which proves the feasibility and effectiveness.

Key Words： missiles； aerodynamic characteristics； Boosting； Gradient Boosting； Bayesian optimization