空间向量与立体几何单元测试(B卷)答案与提示

一、单选题

1.C 2.A 3.B 4.D 5.A 6.C 7.C 8.A

二、多选题

10.BCD 取EF的中点H,连接EH,CH(图略),则,A 错误。

其俯视图如图1所示,可得点C的坐标为(-2,2,2),O,E,F,A四点共面,B,C正确。

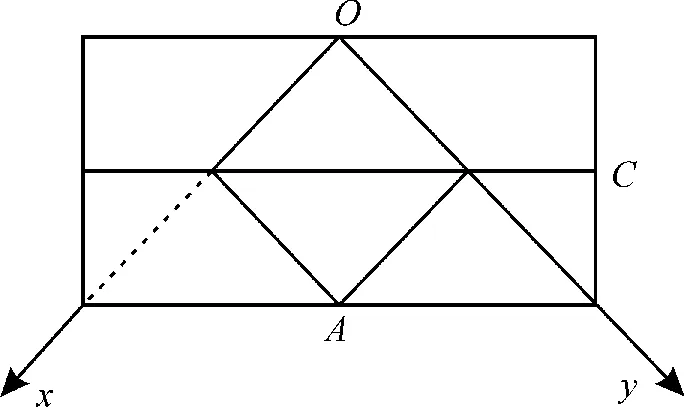
图1

11.AD 提示:由题意,平面α,β,γ两两互相垂直且有一个公共点O。

不妨将平面α,β,γ放置在正方体ABCO-A1B1C1O1的三个相邻面中,记平面ABCO为平面α,记平面AOO1A1为平面β,记平面OCC1O1为平面γ,则直线l1为OA,直线l2为OO1,直线l3为OC。

记正方体ABCO-A1B1C1O1棱长为1。

以点O为坐标原点,OA、OC、OO1所 在直线分别为x、y、z轴建立空间直角坐标系O-xyz,如图2。

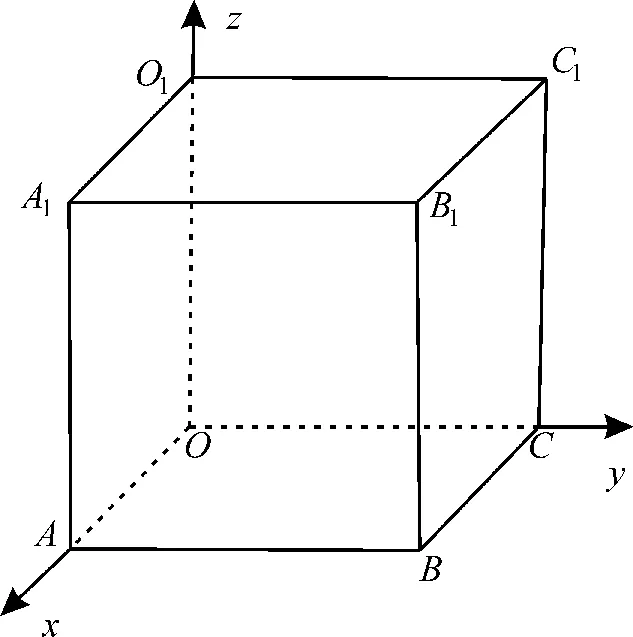
图2

则点O(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),O1(0,0,1),A1(1,0,1),B1(1,1,1),C1(0,1,1)。

又直线l过点O,再取l上一点P,设点P(a,b,c)。

易知平面γ的法向量为m=(1,0,0),设l与平面γ所成的角为θ。

对于选项B,易知平面α的法向量为n=(0,0,1),平面β的法向量为t=(0,1,0)。

若l与平面α,β,γ所成的角相等,则三个线面角的正弦值相等。

所以|a|=|b|=|c|,即P(a,a,a)或P(a,-a,a)或P(a,a,-a)或P(a,-a,-a),则这样的直线l有4条,B错误。

对于选项D,因为点P在l1,l2,l3的投影分别为P1,P2,P3,则P1(a,0,0),P2(0,0,c),P3(0,b,0)。

所以|P1P2|2+|P2P3|2+|P1P3|2=[(a-0)2+(0-0)2+(0-c)2]+[(0-0)2+(0-b)2+(c-0)2]+[(a-0)2+(0-b)2+(0-0)2]=2a2+2b2+2c2。

又2|OP|2=2[(a-0)2+(b-0)2+(c-0)2]=2a2+2b2+2c2,所以2|OP|2=|P1P2|2+|P2P3|2+|P1P3|2,D 正确。

12.ABD 提示:对于A,以D为原点,以DA,DC,D1D所在直线为x轴,y轴,z轴建立空间直角坐标系,如图3所示。

因为正方体ABCD-A1B1C1D1的棱长为2,所以A(2,0,0),D(0,0,0),C(0,2,0),B1(2,2,2),D1(0,0,2),B(2,2,0)。

因为DP⊄平面AB1C,所以DP//平面AB1C,故A 正确。

对于B,设点F到平面ABB1的距离为h,则VB-AB1F=VF-BAB1=S△BAB1·h。点F在正方体的面CC1D1D内(含边界)移动,又因为平面DCC1D1//平面ABB1,所以点F到平面ABB1的距离h为定值。

又因为S△BAB1为定值,所以三棱锥BAB1F的体积为定值,故B正确。

对于D,如图4 连接B1C,B1D1,由正方体的性质知,D1C//A1B,D1C⊄平面A1BD,A1B⊂平面A1BD,所以D1C//平面A1BD。

图4

B1C//A1D,B1C⊄平面A1BD,A1D⊂平面A1BD,所以B1C//平面A1BD。D1C∩B1C=C,所以平面D1B1C//平面A1BD。

点F在正方体的面CC1D1D内(含边界)移 动,当F∈CD1,则B1F⊂平 面D1B1C。

则B1F//平面A1BD,则F点轨迹为线段CD1。

取CD1的中点H,连接AD1,AH,而△ACD1为等边三角形,则|AH|=

三、填空题

16.②③④ 提示:由题知,以C点为坐标原点,以CD,CB,CC1所在直线分别为x轴,y轴,z轴,建立如图5所示的空间直角坐标系。

图5

令正方体ABCDA1B1C1D1棱长a=2。

则C(0,0,0),D(2,0,0),B(0,2,0),A(2,2,0),C1(0,0,2),D1(2,0,2),B1(0,2,2),A1(2,2,2),P(1,1,1),Q(1,2,2)。设T(x,y,z)。

又EF和EH为平面EFGH中的两条相交直线,所以BQ⊥平面EFGH。

为使PT⊥BQ,必有点T∈平面EFGH。

又点T在正方体表面上运动,所以点T的轨迹为四边形EFGH。

又|EF|=|GH|=2,|EH|=|FG|=,所以|EF|≠|EH|,则点T的轨迹为矩形EFGH,故③正确。

结合点T的轨迹为矩形EFGH,分类讨论下列两种可能取得最小值的情况:

当z=1,y=0或y=2时,|PT|=1;

当y=1,z=或z=时,|PT|=。

四、解答题

17.(1)连接AE并延长交CD于M,则M为CD的中点。

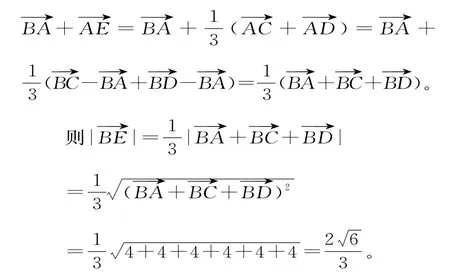
(2)根据题意,BE⊥平面ACD,因此,直线FG与平面ACD所成角的正弦值即为直线FG与直线BE所成角的余弦值的绝对值。

则直线FG与平面ACD所成角的正弦值为。

18.(1)在三棱柱ABC-A1B1C1中,AA1//BB1。

因为BB1⊂平面BB1C1C,AA1⊄平面BB1C1C,所以,AA1//平面BB1C1C。

因为AA1⊂平面AA1EF,AA1EF∩平面BB1C1C=EF,所以,AA1//EF。

因为平面ABC//平面A1B1C1,平面AA1EF∩平面ABC=AF,平面AA1EF∩平面A1B1C1=A1E,所以,A1E//AF。

因此,四边形AA1EF为平行四边形。

(2)因 为AB⊥AC,平 面ABC⊥平 面AA1C1C,平面ABC∩平面AA1C1C=AC,AB⊂平面ABC,所以,AB⊥平面AA1C1C。

以点A为坐标原点,AB、AC所在直线分别为x轴、y轴,平 面AA1C1C内过点A且垂直于AC的直线为z轴,建立如图6所示的空间直角坐标系。

图6

19.(1)因为PC⊥底面ABCD,AC⊂平面ABCD,所以PC⊥AC。

因为|AD|=|CD|=1,AD⊥CD,所以,∠CAD=45°。

又AB//CD,|AB|=2,所以∠BAC=45°,|BC|2=|AB|2+|AC|2-2|AB|·|AC|cos∠BAC=2。

则|BC|2+|AC|2=|AB|2,故AC⊥BC。

因 为PC∩BC=C,PC,BC⊂平 面PBC,所以AC⊥平面PBC。

又AC⊂平面ACF,所以平面PBC⊥平面ACF。

(2)取AB的中点N,连接CN。

因为底面ABCD是直角梯形,AD⊥CD,AB//CD,|AB|=2,|AD|=|CD|=1,所以CN⊥AB。

因为PC⊥底面ABCD,CD,CN⊂平面ABCD,所以PC⊥CN,PC⊥CD。

以C为坐标 原 点, 以CN,CD,CP所在直线分别为x轴,y轴,z轴,建立如图7 所示的空间直角坐标系。

图7

则A(1,1,0),B(1,-1,0),E。设P(0,0,a)(a＞1),则

设平面PAB的法向量为m=(x1,y1,z1),则:

解得y1=0。

令z1=1,得x1=a,故m=(a,0,1)。

20.(1)PA⊥底面ABC,AB,AC⊂平面ABC,所以PA⊥AB,PA⊥AC。

则由旋转可得PA⊥AD,|AB|=|AD|=1,

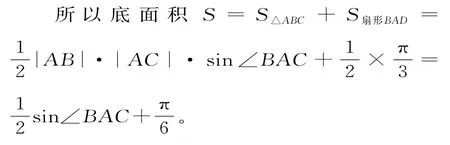
又∠BAC∈(0,π),故当∠BAC=时,sin∠BAC取最大值1。

故当∠BAC=时,该组合体的体积最大,最大值为+。

(2)如图8,以A为 原 点,AC为x轴,AP为z轴,在平面ABC上作y轴,建立空间直角坐标系,则A(0,0,0),C(1,0,0),P(0,0,2)。

图8

综上,直线PC与平面PBD所成角的正弦值为

21.(1)因为AD//BC,所以∠PDA为异面直线PD与BC所成的角,故∠PDA=45°。

又因为AB⊥AD,AP∩AD=A,AP⊂平面PAD,AD⊂平面PAD,所以AB⊥平面PAD。

AB⊂平面ABCD,所以平面PAD⊥平面ABCD。两平面交线为AD,令AD的中点为O,则PO⊥AD,故PO⊥平面ABCD,即PO就是点P到平面ABCD的距离。

又因为|PO|=|AD|=1,所以点P到平面ABCD的距离为1。

(2)延长DE,AB,设DE∩AB=G,连接PG,所以平面PAB与平面PDE的交线l即为直线PG。

又PO⊥ 平 面ABCD,故以O为坐标原点,的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系,如图9。

图9

图10

则P(0,0,1),G(4,-1,0),A(0,-1,0),B(2,-1,0),D(0,1,0)。

又因为PD⊥AP,AB∩AP=A,AB⊂平面PAB,AP⊂平面PAB,所以PD⊥平面PAB。

平面QAB的一个法向量为=(0,-1,1)。

设平面QCD的法向量为n=(x,y,z)。

22.(1)C1D⊥ 平 面ABC,BD,AC⊂平面ABC,则C1D⊥BD,C1D⊥AC。

又△ABC为等边三角形,D为AC中 点,则BD⊥AC。以_D

又BD∩DE=D,BD,DE⊂平面BDE,故A1C⊥平面BDE。

令3-λ=t∈(2,3),则λ=3-t。

锐二面角F-BD-E的余弦值的取值范围为。