全贯流泵在停机过渡过程中的水力特性研究

焦海峰 陈正国 王 文 陈松山

(1.扬州大学水利科学与工程学院,扬州 225100; 2.荆州市水利水电勘测设计院,荆州 434000;3.扬州大学电气与能源动力工程学院,扬州 225100)

0 引言

全贯流泵[1-2]作为一种利用湿定子型潜水电机技术的新型水泵,将电机与叶轮外缘整合为一体,不需要通过传动轴驱动,具有结构紧凑、构造简单等优点,因此比较适合中、小型泵站。在全贯流泵运行过程中,由于停电等突发事故,在停机时泵装置内部截流装置未能成功运行,因此在水压的作用下水流发生倒流,全贯流泵的转动部件在倒流的冲击下反向旋转,逐渐进入飞逸工况[3-4]。在事故停机过程中,由于泵内的水流较为紊乱,各过流部件以及电机容易损坏,因此有必要对全贯流泵在事故停机过程中的瞬态特性进行研究。

国内外学者对全贯流泵的相关研究大多集中在正常运行工况。文献[5]基于熵产理论对全贯流泵的能量特性进行了研究,发现回流间隙会导致泵装置产生额外的水头损失,电机运行需要更多的轴功率,继而引起装置性能的下降。文献[6-7]发现定转子间隙尺寸对全贯流泵的性能影响较大,间隙尺寸的增大不仅会造成装置性能的下降,还会对装置的内部流场也会产生负面影响。文献[8]研究发现间隙的角度会对全贯流泵的性能产生较大的影响,当间隙角度与主流方向一致时,叶轮内的整体流态较好。

目前,与停机过渡过程[9-11]有关的研究主要集中在轴流泵、离心泵以及轴流式水轮机等流体机械上。文献[12]研究了复合离心泵的停机特性,发现泵装置在正常运行时的流量越大,叶轮转速的下降速度越快,停机速度也越快。文献[13]对抽水蓄能电站的水泵工况下的停机过程进行模拟,研究发现机组转速会影响叶轮与导叶之间的压力,活动导叶的关闭规律会影响蜗壳和尾水管进口的压力。文献[14]对灯泡贯流泵机组的停机过程进行了模拟,结果显示:停机速度越快,流量降到零时的转速越低,装置内的压力增幅越大。为缩短机组低速运作时间,可采用分段减速的方式来停机。

为了研究全贯流泵的停机特性,本文对泵装置的停机过程进行瞬态数值模拟,先分析停机过程中流量、转速、转矩、轴向力和径向力等外特性参数的变化规律和特征,然后从内流场、涡以及熵产等方面进行深入分析,探讨停机过程中间隙回流涡的演变规律以及涡与熵产之间的内在联系。由于全贯流泵模型的尺寸较小,电机转子的加工与安装难以实现,因此本文仍将采用传动轴来驱动叶轮。

1 数值模拟

1.1 控制方程

全贯流泵在停机过程中的连续性方程和动量方程分别为

divu=0

(1)

(2)

式中u——速度矢量

ρ——流体密度,kg/m3

p——压力,Pa

F——单位流体上的体积力,N/m3

μ——流体动力粘度,Pa·s

数值模拟计算采用SSTk-ω湍流模型[15-16],该湍流模型由MENTER[17]设计。在修正了涡粘系数的基础上,结合了逆压边界层中湍流剪切力的传输效应。因此SSTk-ω湍流模型适合用于各种压力梯度下的边界层问题的计算。SSTk-ω湍流模型中涉及的涡粘系数vt、输运方程k方程以及ω方程的公式分别为

(3)

(4)

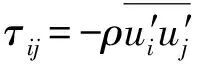
(5)

(6)

式中ui、uj——速度分量

Ω——涡量,s-1

τij——黏性剪切力,Pa

F1、F2——混合函数

a1——系数xj——坐标

β、β′、γ、σk、σω、σω2——封闭常数

k——湍流动能

ω——单位湍动能耗散率

t——时间,s

水泵机组在停机过程中,电动机的拖动力矩、泵机组阻力力矩和惯性力矩共同组成泵机组转动惯性平衡方程[18]

MJ=MD-MW-MZ-MR-MF-MO

(7)

式中MJ——惯性力矩,N·m

MD——电动机的拖动力矩,N·m

MW——水泵的水力矩,N·m

MZ——推力轴承摩擦力矩,N·m

MR——径向轴承摩擦力矩,N·m

MF——电动机风扇损失力矩,N·m

MO——推力头和滑转子受到的油粘滞阻力力矩,N·m

水泵机组转动部件惯性力矩公式为

(8)

式中J——转动惯量,kg·m2

JG——水泵机组转动部件的转动惯量,经计算约为0.2 kg·m2

ω*——叶轮瞬时角速度,rad/s

n——叶轮瞬时转速,r/min

当电机突然断电后,电机的力矩变为零,此时在水流阻力矩的作用下,水泵转轮与电机转子的转速逐渐下降并开始反转。停机过程中忽略风扇阻力、粘油阻力和摩擦阻力,则惯性力矩公式变为

(9)

每一个时间步长的角速度可以迭代计算,公式为

(10)

式中 Δt——时间步长,s

1.2 计算模型与网格

全贯流泵装置的计算模型由叶轮、定转子间隙、进口导叶、导叶、导叶出口扩散段以及进、出水流道7部分构成。其中叶轮和导叶采用SZM35水力模型,叶轮叶片数为4。叶轮轮毂直径D1均为120 mm,叶轮轮缘直径D2为300 mm,定转子间隙dc为1 mm。导叶片数为6,采用扩散导叶型式。进口导叶片数为5,采用直导叶型式。正常运行时水泵的设计转速n为1 421 r/min,设计流量Qd为297.3 L/s。图1为全贯流泵叶轮的三维模型。

图1 全贯流泵叶轮三维模型

由于网格类型和数量会影响数值模拟的精度和计算量,因此泵装置的各部分均划分为结构化网格,且对全贯流泵装置模型进行网格无关性分析,如图2所示。可以看出,在设计工况下,当泵装置总网格数量超过6.91×106时,网格数量的增加对扬程的影响很小,最终选取总网格数量为6.91×106。全贯流泵装置三维模型及各部分网格如图3所示。

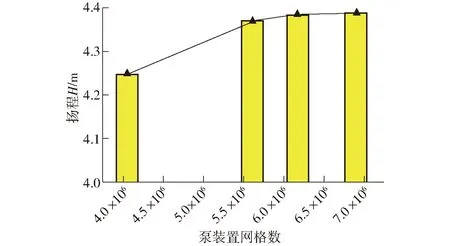
图2 网格无关性验证

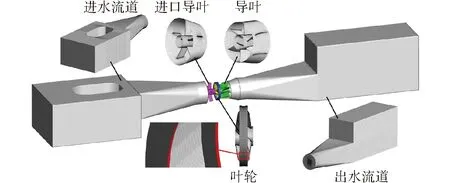
图3 全贯流泵装置计算模型与各部分网格

1.3 停机过程算法实现

在泵站停机过渡过程中,水泵叶轮的转速和转矩是研究停机过渡过程关键的参数。为了实时读取和更新叶轮的转速,通过添加用户自定义程序UDF对软件进行二次开发。其中UDF采用C语言进行编写,通过编译的方式加载到Fluent中,根据力矩平衡方程对整个停机过程的转速、转矩等参数进行控制和计算。在停机过程计算之前需要将稳态计算结果作为初始流场,根据前一时间步长的数据计算得到下一时间步长的叶轮数据。在每一时间步长结束后导出流量、转矩、转速、轴向力、径向力、压力以及间隙回流流量等外特性参数,其计算流程如图4所示。

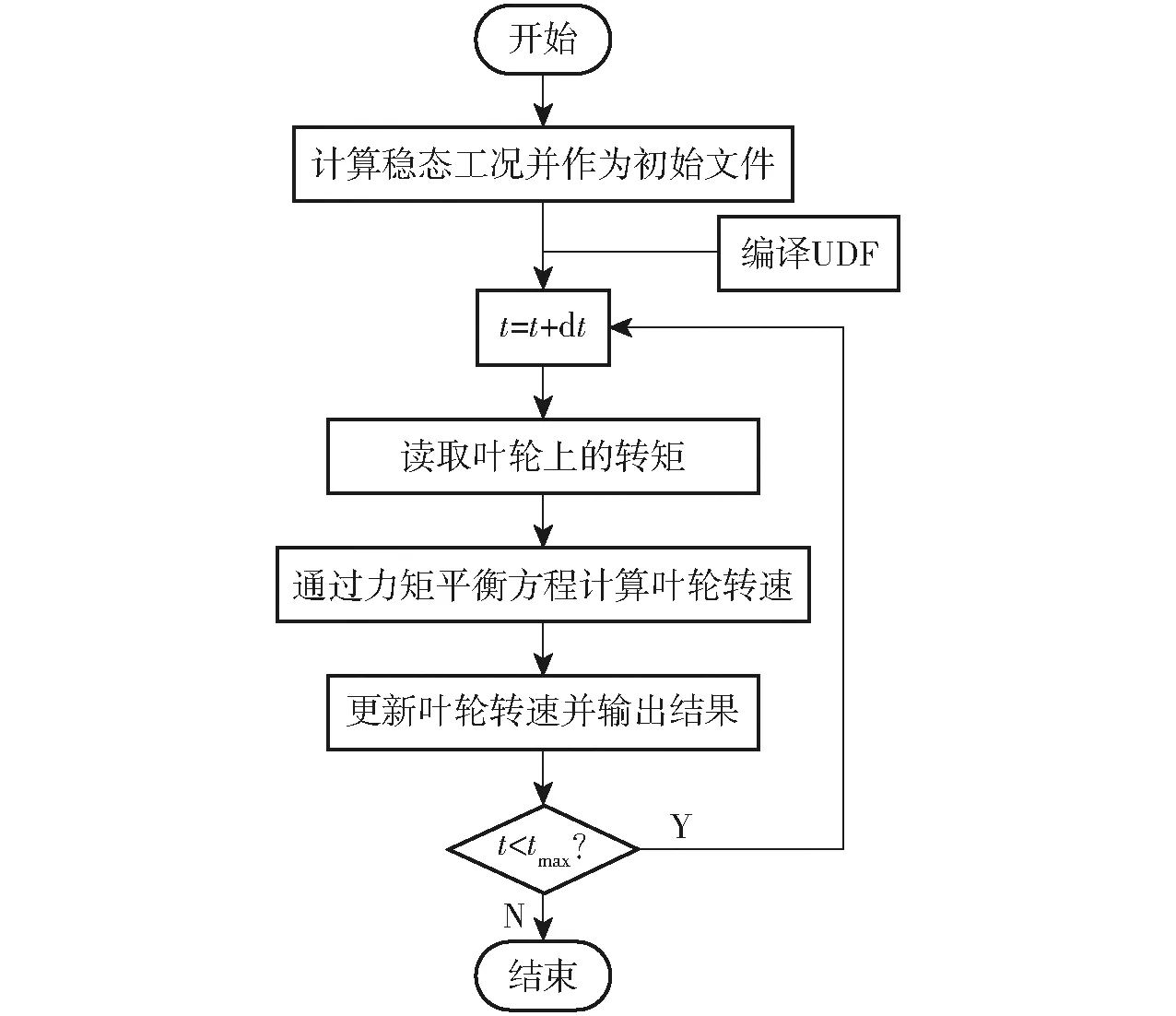
图4 停机过渡过程计算流程图

1.4 边界条件和计算设置

全贯流泵的停机过程采用Fluent软件进行模拟,采用SIMPLE算法。装置进口设置为静压,出口设置为总压。叶轮域设置为旋转域,其他部位设置为静止域。固体壁面包括叶片表面、轮毂表面、轮缘表面、定转子间隙壁面以及进出水流道的壁面等。边界采用满足粘性流体的无滑移条件。对全贯流泵的停机模拟,设置上下游水头差Δh为1.2 m。由于计算资源与计算准确度的限制,在模型泵转速为1 421 r/min的情况下,时间步长设置为0.02 s,每个时间步长最大迭代步数为20步,计算总时长为16 s。

2 模型试验

2.1 试验台介绍

全贯流泵装置的模型试验在扬州大学高精度水力机械试验台上进行,试验系统三维图如图5所示。试验分为外特性试验和压力脉动试验两部分,试验转速n为1 421 r/min。全贯流泵装置实体模型与数值计算模型的尺寸一致,各部件均经过精加工。压力脉动传感器M1、M2和M3分别布置在进口导叶进口、叶轮进口和叶轮出口,采样频率为1 kHz,采样时间为20 s。全贯流泵的叶轮和导叶采用SZM35水力模型,其中叶轮叶片数为4片,采用黄铜材料加工而成,导叶叶片数为6片,采用扩散叶片型式。进口导叶叶片数为5片,采用直叶片型式。进口导叶和导叶均采用厚度为5 mm的不锈钢材料加工成型。转子采用塑钢材料加工并安装在叶轮的外缘。全贯流泵装置实物及压力脉动测点布置如图6所示。

2.2 数值模拟准确性验证

引入无量纲参数扬程系数Hc和流量系数Qc将全贯流泵装置试验与模拟的扬程曲线进行对比,计算公式为

(11)

(12)

式中Hd——设计扬程,m

Q——流量,kg/s

从图7可知,全贯流泵装置数值计算和试验的扬程曲线在设计工况和大流量工况下吻合较好,在小流量下偏差较大但不超过3%,这说明全贯流泵计算模型的精度达到要求。

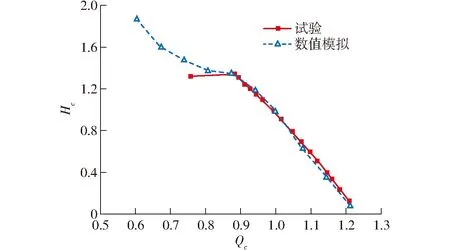
图7 外特性试验与数值模拟结果

引入无量纲参数压力脉动系数Cp

(13)

u——叶轮出口圆周速度,m/s

将叶轮进口M2的压力脉动试验结果与计算结果进行对比,如图8所示。可以发现,叶轮进口测点的压力脉动主频率为94.73 Hz,该频率为1倍的叶轮通过频率。压力脉动计算结果与试验结果在主频幅值上存在较小的偏差,因此认为双向全贯流泵装置的瞬态数值模拟结果是可信的。

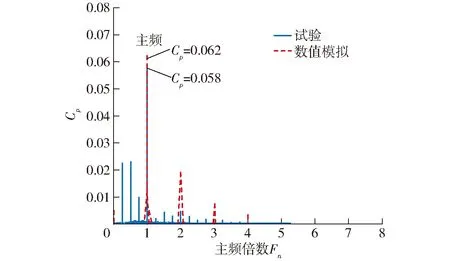
图8 叶轮进口压力脉动数值计算与试验结果

3 数值模拟结果分析

3.1 外特性

全贯流泵在停机过程中各外特性参数随时间的变化如图9所示。从图中可以发现,全贯流泵在停机过程中,泵的转速和流量逐渐由正变为负,转矩逐渐降为零。全贯流泵停机历时约为7.478 s,在此期间泵装置先后历经水泵工况、制动工况、水轮机工况以及飞逸工况。全贯流泵停机过程中在水泵工况、制动工况、水轮机工况历时分别为2.178、0.387、4.913 s,其中制动工况历时占整个停机过程的比值最小。工况变换的3个时间节点t1、t2和t3分别为2.178、2.565、7.478 s。在整个停机过程中,全贯流泵停机过程转速的下降率为180%。

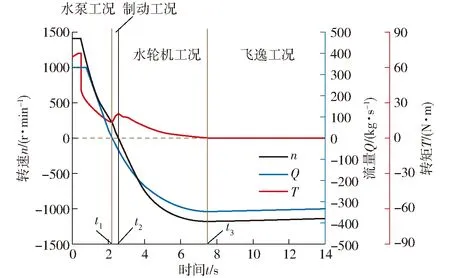
图9 全贯流泵在停机过程中各外特性参数的变化

在t=0.5 s时,水泵电机突然断电,电动机的拖动力矩MD为零,在水阻力矩和轴承摩擦力矩等的作用下,水泵的转速迅速下降,流量和叶轮力矩也迅速下降,该过程一直持续到t1时刻流量降为0 kg/s时结束。在上下游压差的作用下,水泵的转速继续下降,水流开始倒流,反向流量逐渐增大,叶轮扭矩逐渐增大,直到转速下降为0 r/min时(t2时刻)达到峰值。当反向流量进一步增大时,叶轮开始反向旋转,泵装置进入制动工况。随着转矩进一步减小,叶轮反向转速的增大率逐渐减小,直至转矩降低为零,叶轮的反向转速和流量达到最大值并趋于稳定,泵装置进入飞逸工况。全贯流泵的飞逸转速约为设计转速的84%,飞逸流量为设计流量的1.17倍。

图10为全贯流泵在停机过程中转子径向力Fr与轴向力Fa随时间的变化。从图中可以发现,在水泵工况轴向力Fa急剧降低,在制动工况轴向力有小幅度增大,随后在水轮机工况轴向力逐渐降低,直至进入飞逸工况轴向力趋于稳定。转子径向力在水泵工况逐渐减小,在制动工况基本没有变化,然而当装置进入水轮机工况后转子径向力突然增大,直至进入水轮机工况趋于稳定。全贯流泵的转子径向力在5.69 s时达到最大值。

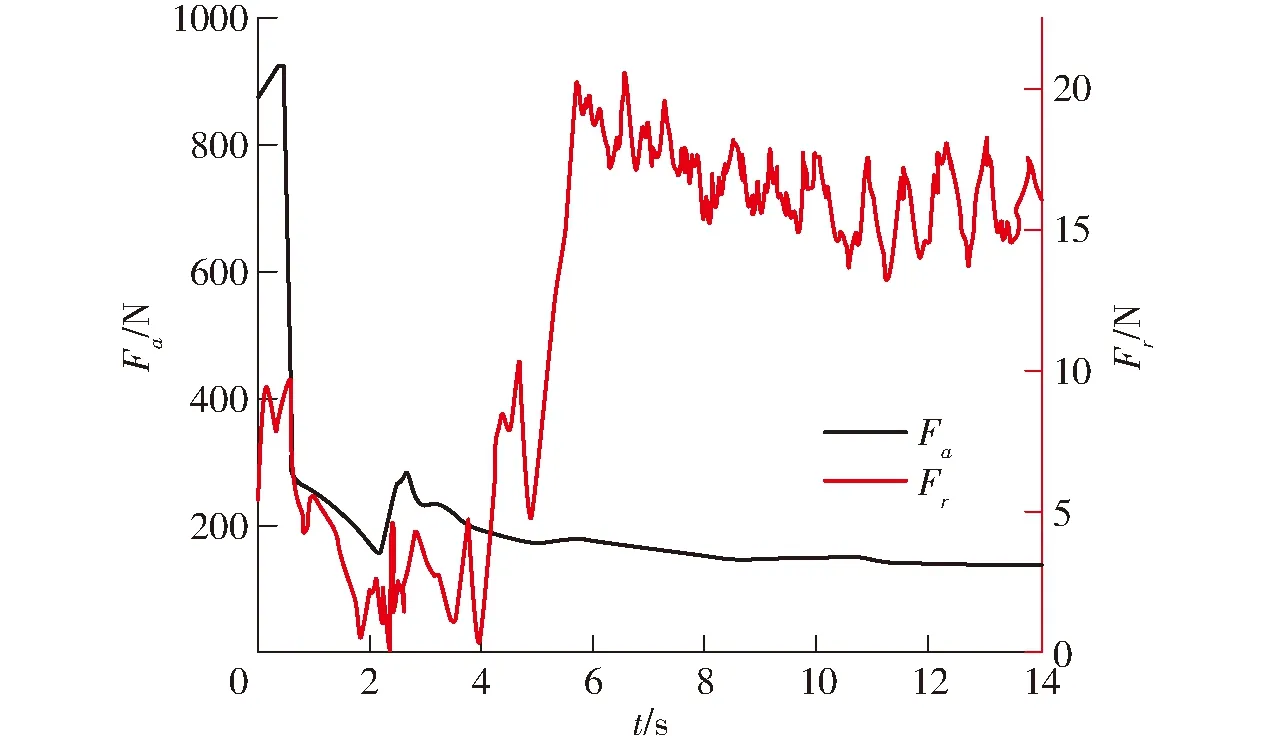
图10 停机过程中轴向力与径向力的变化

由于全贯流泵的定转子中间存在间隙,因此在压差的作用下该间隙内会存在间隙回流。停机过程中全贯流泵内的间隙回流流量Qc,如图11所示。可以发现,在全贯流泵停机过程中,间隙回流流量在水泵工况下迅速减小,在制动工况有小幅度的增大,最后在水轮机工况又迅速降低并稳定在最小值(约0.1 kg/s)。

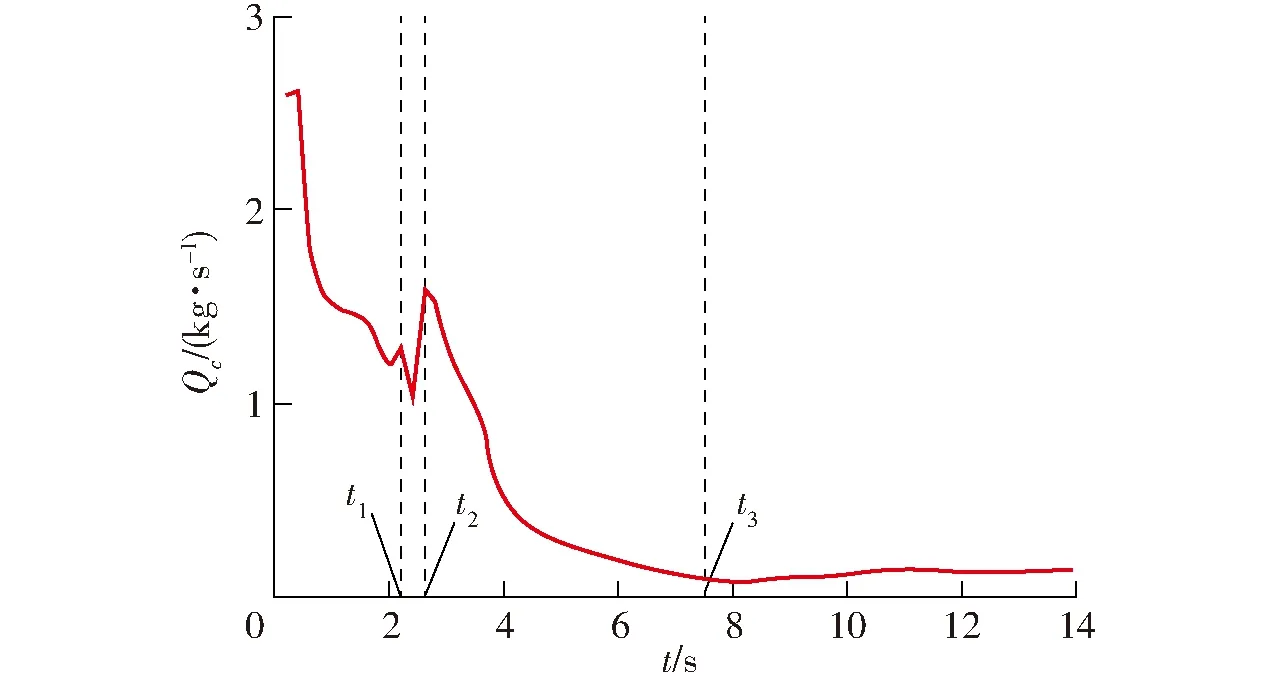
图11 停机过程中间隙回流流量Qc的变化

为了分析停机过程中装置内部压力脉动的变化,沿轴向对装置内部14个压力脉动监测点的压力脉动系数最大的绝对值进行分析,如图12所示。其中叶轮进口测点P6以及出口测点P7随时间的变化如图13所示。从图12可以看出,越靠近叶轮,全贯流泵装置内部的压力脉动越强。全贯流泵叶轮进口的压力脉动幅值最大,约为叶轮出口的2倍。从图13 可以看出,在停机过程中,全贯流泵叶轮进出口的压力脉动均先减小后增大,在制动工况达到最大值后,在水轮机工况迅速减小,直至进入飞逸工况趋于稳定。

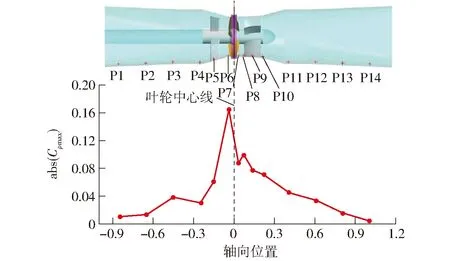
图12 泵装置内压力脉动最大值随轴向位置的分布

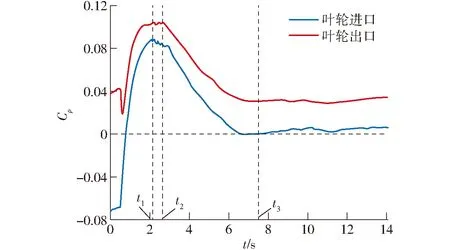
图13 停机过程中叶轮进、出口的压力脉动变化

3.2 内流场

全贯流泵停机过程中,由于叶轮出口压力始终大于叶轮进口,因此间隙回流始终存在,且其流量随着时间的增大越来越小。为了方便分析间隙回流对全贯流泵内部流态的影响,全贯流泵停机各时刻叶轮与定转子间隙内(图14,图中LE、TE分别表示叶片前缘、后缘)的压力分布与流线图如图15所示。从图中可以发现,在正常运行工况,全贯流泵叶轮内的流态较为平顺,叶轮进口处由于受到间隙回流的影响,在靠近轮缘区域出现一个小型旋涡,旋涡区域压力较低。当t=0.8 s时,此时泵装置进入水泵工况,由于间隙回流流量的减小,叶轮进口旋涡和低压区的范围较正常工况有所减小。当泵装置进入制动工况后,叶轮内的压力减小,水流开始倒流,叶轮在主水流的作用下转速逐渐减低,叶轮内的流态变得非常紊乱。由于制动工况下间隙回流流量有短暂的增大,因此叶轮进口回流与旋涡的区域达到最大,叶轮出口也出现了大面积的偏流。在t=2.2 s时刻,全贯流泵叶轮进口旋涡向叶轮进口的方向转移,且旋涡的范围有所增大。与此同时,由于主流与间隙回流的相互作用,在间隙出口与叶轮之间也出现了一个旋涡。最后进入水轮机工况和飞逸工况,全贯流泵的倒流流量增大,全贯流泵叶轮进口靠近轮缘区域仍存在旋涡和偏流等不良流态,但由于间隙回流流量的进一步减小,叶轮进口旋涡基本消失,只存在局部偏流,整体流态相对制动工况有所改善。整体来看,全贯流泵在停机过程中间隙回流涡逐渐向叶轮进口侧转移,且该旋涡的范围呈现先减小后增大再减小的区域,其中制动工况下叶轮内的流态最差。

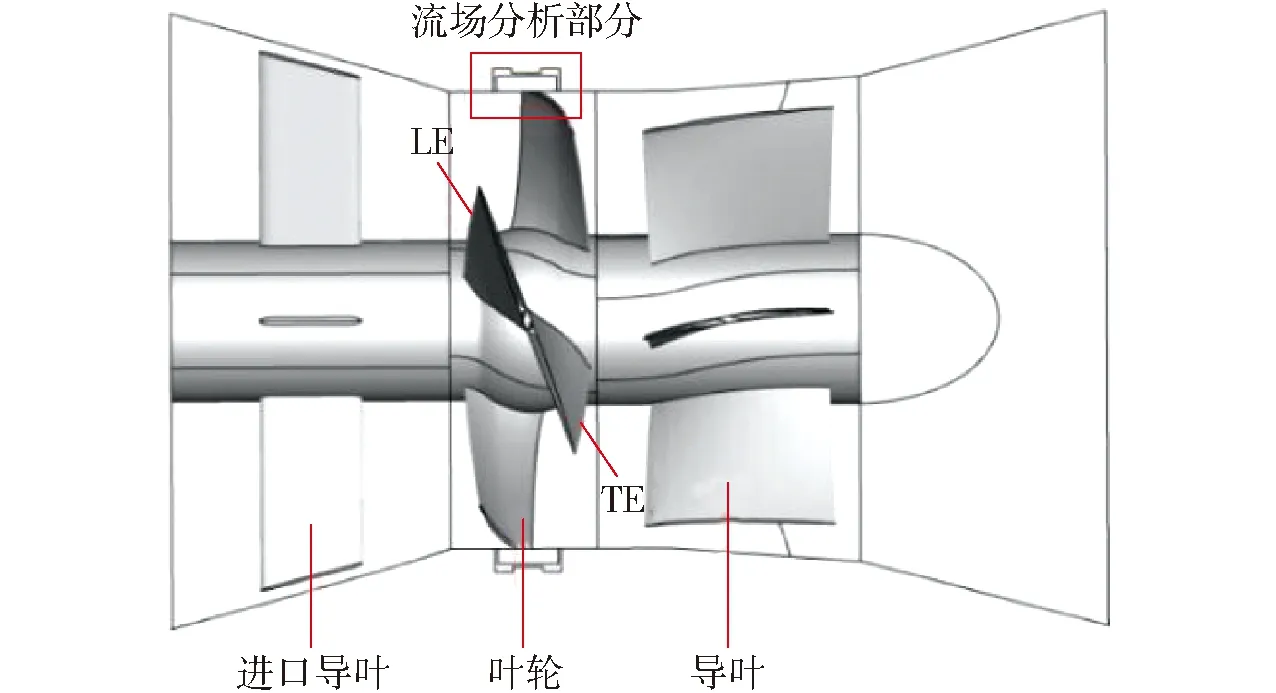
图14 全贯流泵泵段参数示意图

3.3 涡识别

从压力场和流线图的分析中发现间隙回流会导致叶轮进出口产生不同程度的旋涡,因此为了更深入地分析停机过程中全贯流泵内涡的变化,基于Omega涡流识别方法[19-21]全贯流泵在停机各时刻泵段内的涡分布如图16所示。

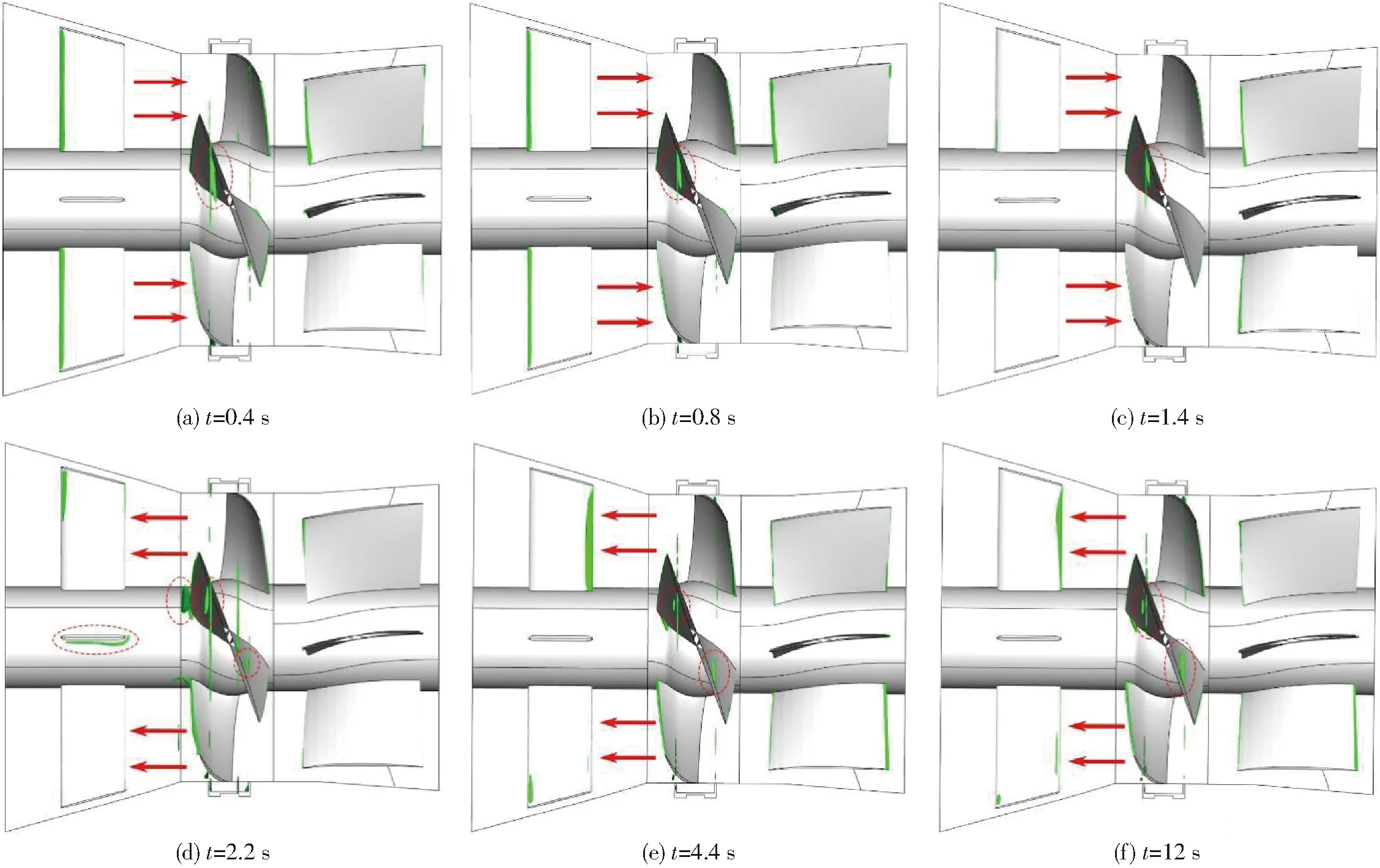
图16 停机各时刻泵段内的涡流分布

从图16可以发现,在全贯流泵停机过程中,间隙回流始终会导致叶轮进口产生回流旋涡,该回流旋涡发生在间隙出口与叶片吸力面交界处。当进入水泵工况后,进口回流旋涡随着间隙回流流量的减小而减小。当进入制动工况,叶轮进口出现两个回流旋涡且尺寸较其他工况大,这与图15的结果一致;由于此工况下水流刚开始倒流,水流流态十分紊乱,进口导叶片表面也存在旋涡。除此之外,当泵装置进入制动工况后(t=2.2 s),由于主流开始倒流,间隙出口与叶轮压力面交界处也产生旋涡,且该旋涡尺寸在停机过程中逐渐增大。

3.4 熵产

由于全贯流泵停机过程中叶轮等部件内始终存在着旋涡、回流和流动分离等不良流态,因此装置内部无时无刻不在发生着能量损失,装置中的熵增量总是大于零。为系统分析装置内部流动不稳定区域,将能量损失可视化,对泵装置内部的熵产[22-24]进行计算。由于水的比热容较大,计算忽略了能量转化引起的熵产。图17为停机过程中泵装置各部分的熵产随时间的变化。

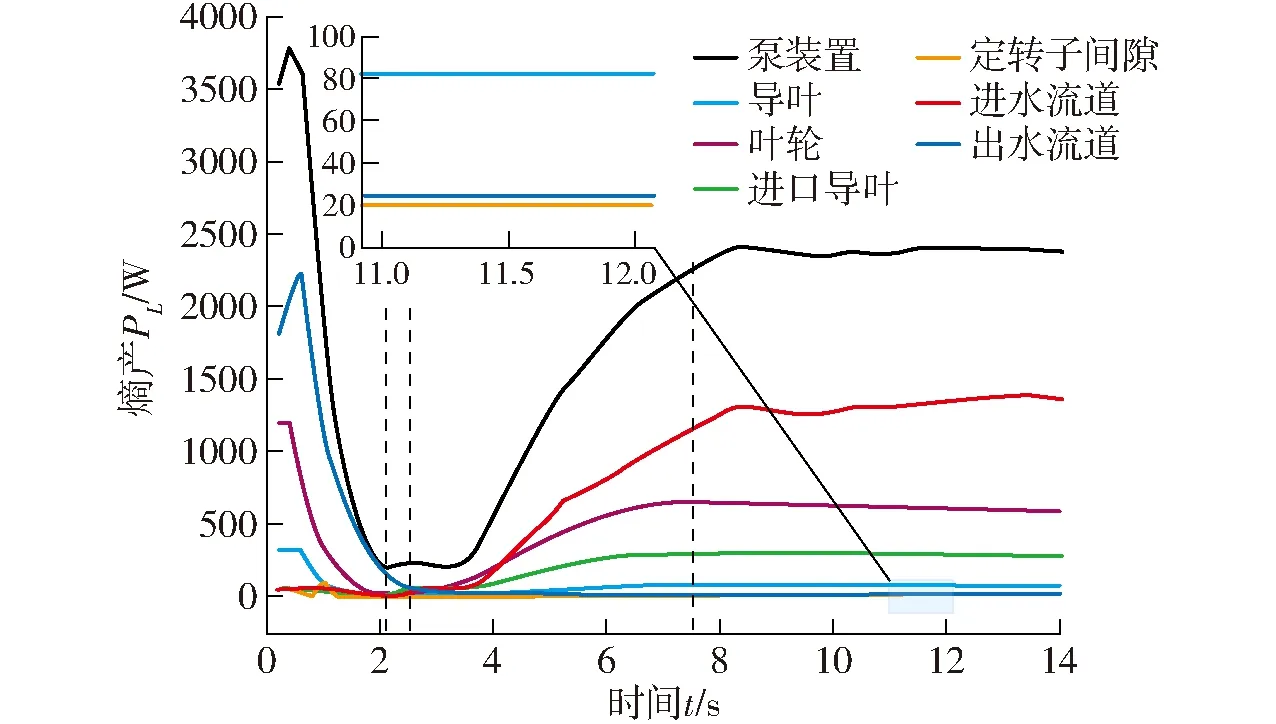
图17 全贯流泵停机过程中泵装置各部分的熵产变化

从图17可以发现,在停机过程中,全贯流泵各部件的熵产变化趋势相同。随着工况的变化先减小后增大,最后在飞逸工况保持稳定,其中制动工况下的熵产最小。在停机过程中,装置内部的熵产主要集中在以叶轮为首的下游域,其中在正常工况、水泵工况和制动工况下,熵产主要集中在出水流道、叶轮和导叶;而在水轮机工况和飞逸工况下,由于水流倒流,熵产主要集中在进水流道、叶轮和进口导叶。由于电机断电后叶轮做功能力急剧下降,叶轮的转速和流量迅速降低,水流在流经叶轮之后出现旋涡、回流和流动分离等不良流态,因此叶轮内的速度梯度较大,继而导致叶轮内的熵产始终较大。在水轮机工况,随着反向流量的增大,各过流部件内的熵产也增大。直到进入飞逸工况,泵的转速和流量达到反向最大值,泵装置内的熵产也趋于稳定。由于飞逸转速小于正常运行时的转速,因此飞逸工况下泵装置内的熵产也小于正常运行工况。

由于全贯流泵内的水力损失主要集中在叶轮、导叶与进口导叶内,因此泵段在叶片高度Span值为0.97下(图18)的熵产率云图如图19所示。从图中可以发现,在停机过程中,全贯流泵内的高熵产率区域主要集中在叶轮、导叶以及进口导叶叶片的表面,这是由于水流在流动时与叶片激烈冲撞,在叶片表面产生流动分离和旋涡等不良流态,高速水流与低速水流之间发生剧烈的能量交换。

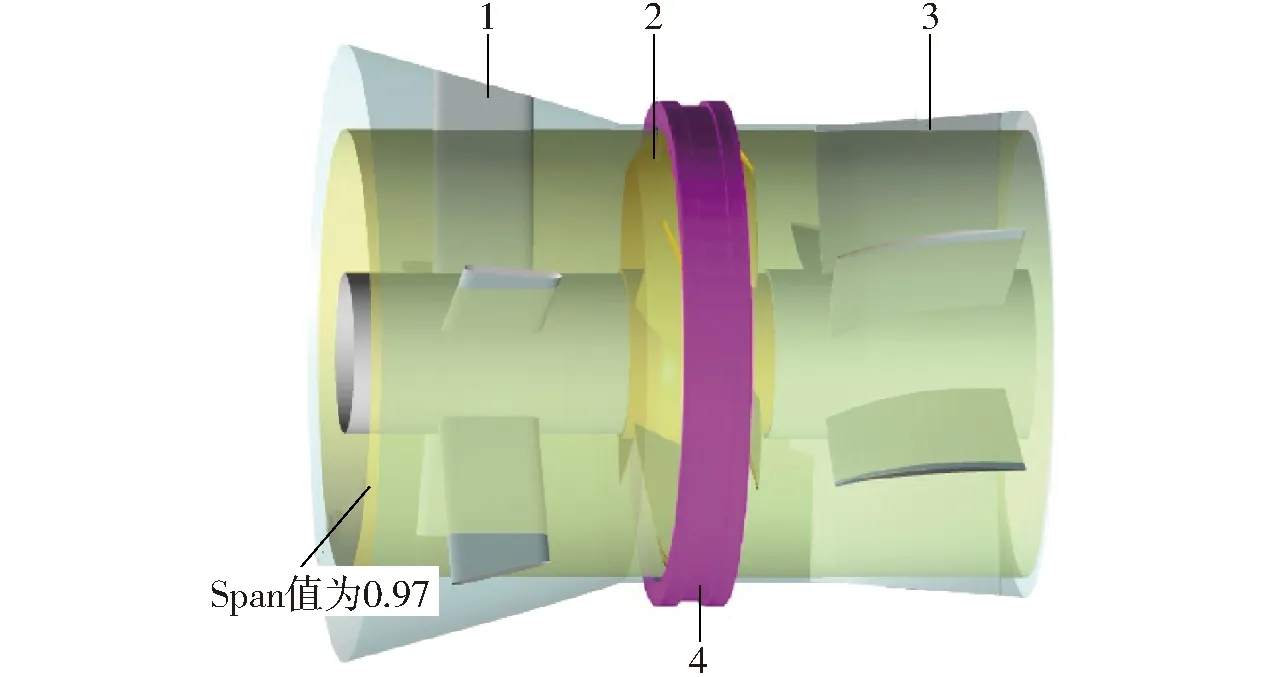
图18 叶片高度示意图

图19 停机各时刻泵段内部的熵产率分布

整体来看,随着停机过程的发展,水流开始倒流,泵装置内的高熵产区域逐渐向进口导叶的方向转移,高熵产区域的范围先减小后增大。从图19a可以看出,在水泵工况下高熵产率区域主要集中在叶轮叶片吸力面以及叶轮与导叶之间的无叶区,高熵产率区域起始于叶轮吸力面与间隙回流出口交界处。图19b、19c为泵装置停机0.8 s和1.4 s时的熵产率分布,叶轮和导叶内高熵产率的分布与水泵正常运行时一致,但由于转速的降低,高熵产率的范围也有所减小。图19d为泵装置进入制动工况,此时水流开始出现倒流,在叶轮、导叶和进口导叶叶片的表面存在着明显的流动分离,泵内的高熵产率区域转移到叶片压力面,由于此时流量较小,高熵产率范

围较水泵工况有所减小。图19e为泵装置进入水轮机工况,随着倒流流量的进一步增大,叶轮叶片压力面的流动分离加剧,水流速度梯度增大,高熵产率范围开始增大,直至进入飞逸工况趋于稳定。

泵段内高熵产率区域的位置和范围与图16中旋涡出现的位置和尺寸相对应,这表明旋涡与脱流等不良流态是导致全贯流泵段内部熵产率较高的主要原因,也说明通过数值模拟的方法来对全贯流泵的停机性能进行分析是可行的。

4 结论

(1)全贯流泵在停机过程中先后历经水泵工况、制动工况、水轮机工况以及飞逸工况,其中制动工况所用时间占整个停机过程比值最小。飞逸转速约为设计转速的84%,飞逸流量为设计流量的1.17倍。在停机过程中,轴向力在停机过程中呈现下降的趋势;转子径向力在停机过程中呈现先减小后增大的趋势;间隙回流在停机过程中流向不变,始终从叶轮出口流向叶轮进口,且其流量逐渐减小;全贯流泵叶轮进、出口的压力脉动均先减小后增大,在制动工况达到最大值后,在水轮机工况迅速减小,直至进入飞逸工况趋于稳定。距叶轮越近,压力脉动越强,全贯流泵叶轮进口的压力脉动幅值最大,约为叶轮出口的2倍。

(2)由于受到间隙回流的影响,在叶轮进口靠近轮缘区域存在一个小型旋涡。在停机过程中,叶轮进口旋涡的尺寸在水泵工况逐渐减小,直至进入制动工况开始增大,最后在水轮机工况和飞逸工况又逐渐减小;叶轮进口旋涡的位置随着主流方向的改变,逐渐由间隙出口与叶轮之间转移到叶轮与进口导叶之间。

(3)随着停机过程的发展,泵装置内的熵产呈现先减小后增大的趋势,高熵产区域逐渐向进口导叶的方向转移。在停机过程中,全贯流泵内部的熵产主要集中在以叶轮为首的下游域。在水泵工况下的高熵产率区域主要集中在叶轮吸力面以及叶轮与导叶之间的无叶区,高熵产率区域起始于叶轮吸力面与间隙回流出口交界处。全贯流泵叶轮内高熵产率区域的位置和范围与旋涡出现的位置和尺寸存在对应关系,这表明旋涡与脱流等不良流态是导致全贯流泵装置过流部件处熵产率较大的主要原因之一。