基于SSA-RFR算法的采棉机测产传感器研究
2023-09-23伟利国马若飞周利明隗立昂刘阳春
伟利国 马若飞 周利明 隗立昂 刘阳春 赵 博
(1.中国农业机械化科学研究院集团有限公司,北京 100083; 2.农业装备技术全国重点实验室,北京 100083)
0 引言
棉花作为我国主要大田经济作物之一,其产业链长且涉及多个行业,在国民经济发展中占据重要地位。2020年我国仅新疆维吾尔自治区皮棉总产量5.161×106t,占全球总量的20%以上。面对日益增长的棉花需求量,实施精准农业,是我国棉花增产增收发展的方向。作物产量监测是精准农业技术的重要组成部分,获取棉花产量分布图,可作为精准农业系统信息反馈,也可检验精准农业技术的实际实施效果,同时为下一季棉花生产精准控制提供原始数据信息。因此,开展棉花产量动态监测系统的研究,具有实际意义[1-3]。
美国从20世纪90年代末开始研究棉花的产量监测系统。最先由WILKERSON等[4]提出基于光线密度变化的产量检测方法,用线性关系标定质量流量和传感器输出,决定系数0.93,在改进后由Ag Leader公司投向市场。SUI等[5]设计了反射式光电传感器,降低了安装难度,在密西西比州进行了3年田间实验,检测误差率5%。MAILANDER等[6]对输棉管道内压差和不同含水率的棉花质量流量进行研究,并建立关系模型,实验显示测量误差不大于13%。SANH[7]设计的质量流量计,可以实时检测加工过程中棉花的质量,其由2个S形应变片组成,经过实验验证,其精度可以达到±5%。国外经过多年发展,现在已有较为成熟的棉花质量在线检测系统,如凯斯(CASE)的精准农业系统(AFS),Ag Leader的PF3000以及Insight系统等,都有较好的表现[8]。
国内学者在棉花测产系统上也有一定的研究成果。何晓峰等[9]利用近红外方法,提出拟合优度更好的双指数数学拟合,决定系数R2达到0.99。安光辉[10]以五通道的光电传感器为基础,通过回归分析,确定每个通道在回归中的权重,台架实验绝对误差平均值5.67%。周利明等[11]设计了一种差分结构的电容质量流量传感器,建立含水率、质量流量和电容变化率的二元回归模型,实验验证误差5.16%。王欢[12]设计的光电点阵式测产传感器,经过处理后建立流经传感器的棉花团三维模型,换算得到产量,实验结果相对误差4.31%。目前检测棉花质量流量的方法较多,但大多数方法在田间实验时表现不佳,目前广泛采用的检测方法仍为光电对射法。随着机器学习热潮的到来,其在棉花测产上也有了一定的应用。任玲等[13]论证了应用神经网络进行棉花质量建模的分析方法的可行性,并分析了神经网络建模的过程。岑红蕾等[14]在光电测产传感器上,引入BP神经网络标定质量流量和辐射量,实验验证相对误差7.84%。林昌建等[15]基于现有的光电测产传感器,引入广义神经元网络进行产量标定,并使用改进遗传算法对网络进行改进,实验验证平均误差最小7.3%。检测精度较传统方法有所上升,说明该方法具有一定的研究潜力。
在训练机器学习模型时,超参数的选择对模型预测精度影响较大[16],若在没有先验经验的情况下,能通过寻优算法,高效、准确得到模型超参数,将进一步提高模型检测精确度以及减少模型运算成本。
本文在现有光电对射式测产传感器的基础上,对现有传感器进行优化和改进,并在标定产量关系时,运用将麻雀优化算法和随机森林回归模型融合后的模型来检测棉花产量。最终利用台架实验加以验证,并对比未经优化的随机森林回归模型,分析建立最优模型。
1 传感器优化设计
1.1 传感器检测原理
如图1所示,光电对射式测产传感器检测原理是利用棉花通过采棉机输棉管道时,遮挡安装在输棉管道上的传感器发射器发射的红外辐射,接收器通过检测辐射强度的变化,并在完成辐射强度和棉花质量之间的关系标定后,即可在线检测采棉机作业时的棉花产量。
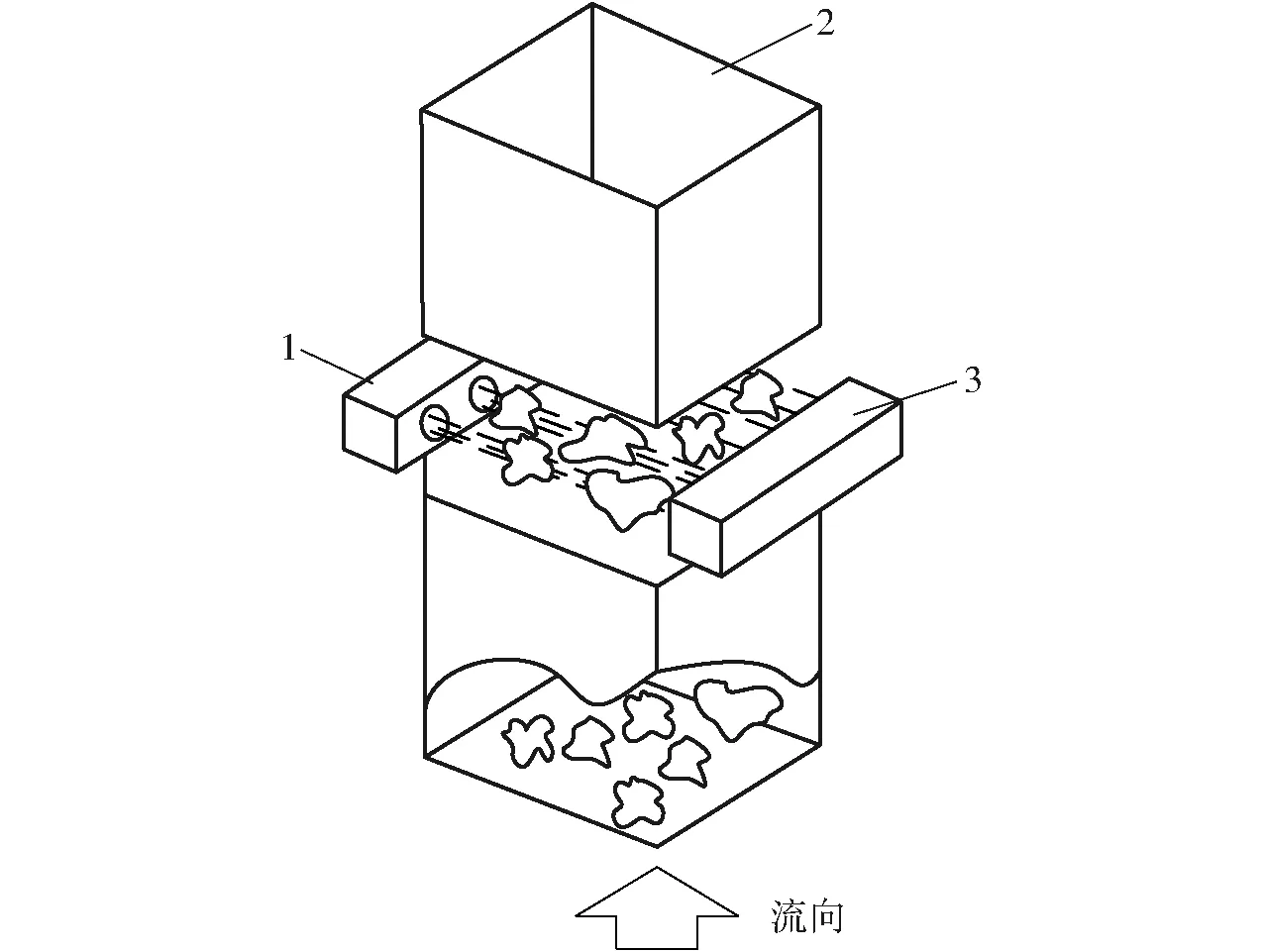
图1 检测原理示意图
本传感器通过检测每个设定的单位时间内棉花产量,依次得到作业轨迹上各个小田块内棉花产量,最后整合呈现整块地的产量,检测原理公式为
m=g(H1,H2,…,H6)
(1)
式中m——单位时间内检测的棉花质量,g
Hi——单位时间内辐射强度变化向量
1.2 结构优化
本文以中国农业机械化科学研究院集团有限公司机电技术应用研究所团队研发的采棉机测产传感器为基础,针对其在实际作业中存在的问题进行优化改进。
现有的传感器在获取发射器准直光路时,均通过普通凸透镜实现,这种方法需要将光源较为准确地放置在透镜的焦点处,这对安装和加工提出了较高的要求。通过查阅资料,全内反射(TIR)透镜较普通凸透镜有更好的聚光效果,安装时不需人为手动寻找透镜焦点,且形成的光斑也更加自然[17]。因此,本文用TIR透镜替换凸透镜,并在透镜的安装孔处进行了相应的修改。
周利明[18]调查发现,因脱叶剂喷洒等原因,造成传感器发射器易被灰尘、叶片以及脱叶剂所形成的黏浆所遮挡,使传感器不能正常工作。因此,本文在传感器上,采用透镜安装孔内嵌的结构,使其不阻碍棉花通过传感器。而特弗伦材料对防止黏浆粘黏有较好的表现[19]。故在透镜外加装一层特弗伦材质的防护层,保证传感器检测光路不被遮挡。
LED红外发射管会随着工作时间的增加而发热,使发射管发射辐射强度发生变化[20],导致检测结果出现偏差。因此,本文增加一路校验通道,通过安装在连接板上的隔板使该通道与其他检测通道相隔,只检测空载值。传感器结构示意图如图2所示。
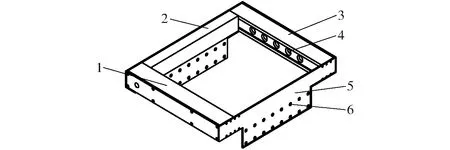
图2 传感器结构示意图
因每个发射管均为同一型号且用相同的供电电源,故其因工作时间导致的温度变化基本相同。所以只需将同一时刻的检测通道的数据减去校验通道的数据,即可修正因温度改变辐射源强度而导致的检测偏差,修正原理公式为
Lk=Wk-W0(k=1,2,…,5)
(2)
式中Lk——某时刻通道k补偿后的辐射强度
Wk——某时刻通道k输出的辐射强度
W0——某时刻校验通道输出的辐射强度
1.3 硬件优化
经过验证得到使用940 nm红外辐射源时,棉花品种、含水率对产量检测结果影响较小,而证明年份、色泽对棉花的红外光学特性没有显著影响[21]。因此,本文的红外发射器选用台湾亿光公司生产的IR333-A型940 nm红外发射管,其结构简单,工作稳定。
环境光传感芯片选用AMS公司的TSL2540环境光芯片,该芯片有可见光和红外光2个感应通道,如图3所示。可单独打开红外感应通道,可在一定程度上减小环境光对检测精度的影响。该芯片通过IIC通信协议和下位机进行通信,向外输出频率为2 Hz,输出的数据结构为高、低8位二进制数。
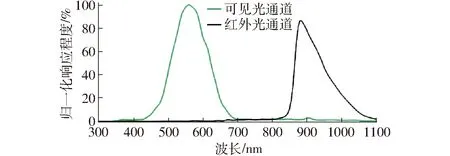
图3 光感芯片特性
在安装时会因连接板上发射器和接收器之间距离有级调节导致初始辐射值发生变化。因此,本文在发射器中加入电流控制模块,通过接收上位机发送的指令,改变供给发射管的电流,而调节红外发射器初始辐射强度,调节信号通过CAN通信协议发送至下位机。
使用STM32F103RCT6作为下位机,用于收集各检测通道检测结果和接收上位机指令信号,使用CAN通信协议。在向上位机发送数据时,因CAN 数据帧格式要求,需将每个采样周期内的数据分两次向上位机发送,传感器工作原理如图4所示。
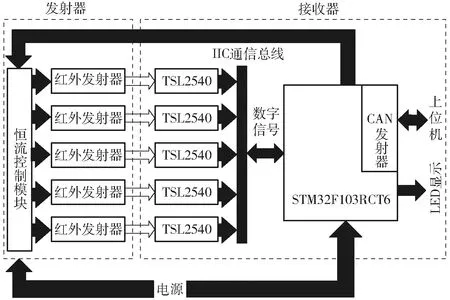
图4 传感器工作原理框图
2 数据集建立
2.1 样本平台
实验棉花样本来源于2021年石河子市采收的新陆早80号,马克隆值4.7,含水率约为7.3%。实验台架由风机、喂棉传送带、输棉管道和集棉网组成。传送带选用2台DGBL60型电动滚筒作为动力源,可实现无级调速;风机选用CF-2A型多翼式离心风机,转速2 800 r/min,风量1 248~2 258 m3/h,全压890~1 150 Pa。风机可以通过变频器调节风速。棉花经过喂棉传送带进入喂棉口,通过风机的作用在输棉管道内飘动,经过测产传感器,最终被集棉网收集。实验台架示意图如图5所示。
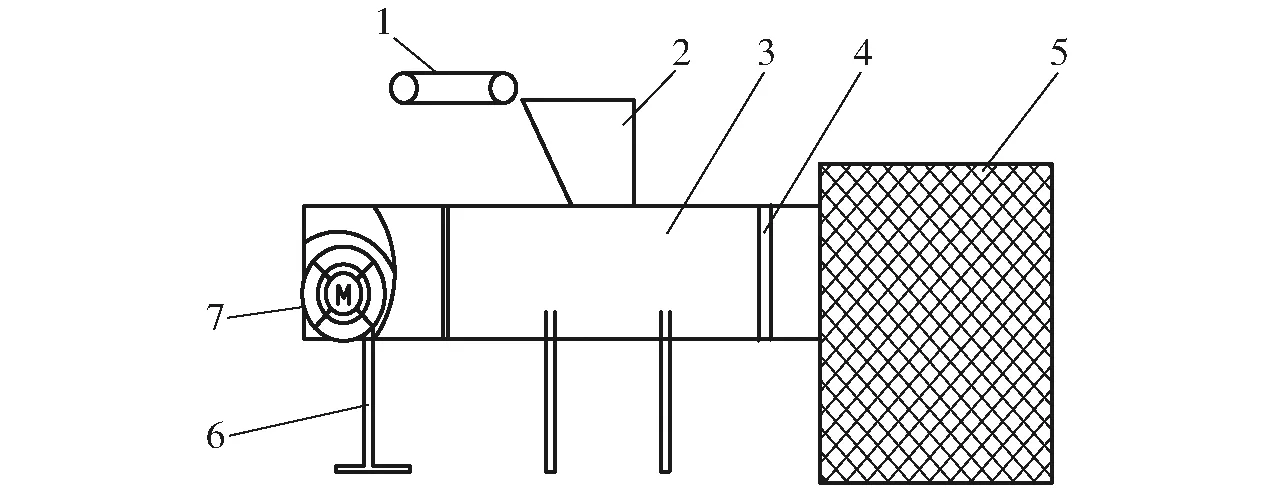
图5 实验台架示意图
2.2 数据获取
每次实验前,用电子秤称量一定量棉花,将其均匀平铺在喂棉传送带上,平铺宽度为250 mm,长度为1 000 mm。设置喂棉传送带传送速度为0.2 m/s,设置风机工作频率为30 Hz。启动风机,等待上位机稳定显示检测数据后,启动喂棉传送带,将其上的棉花经模拟输棉管道上的喂棉口喂入,在风机作用下,流过光电对射式棉花产量检测传感器,最后被铁丝阻拦网收集。进行多次实验,每次实验的风机变频器频率、喂棉传送带传送速度、喂棉传送带棉花平铺长度均不变,只定量增加输棉传送带上的棉花质量。
总共进行200次实验,实验的棉花质量从125 g 开始,每次实验增加125 g棉花,每个质量进行5次实验。图6、7分别为质量125、1 000 g时的4次实验各通道的辐射强度变化图,其中通道6为校验通道。
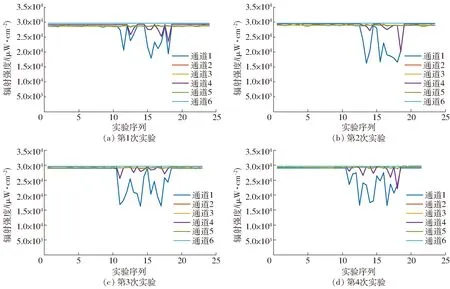
图6 质量125 g时的4次实验各通道的辐射强度变化曲线
由图6、7可以明显看出,随着喂棉质量的增加,每次实验中各通道辐射强度的最大、最小值之差有明显增加,且辐射强度变化曲线和空载值所围成的面积也呈增加趋势,因此,可以将实验中每个通道辐射变化有效值的极差、方差、积分等参数作为代表实验棉花质量的特征。
2.3 数据预处理
首先对所采集到的数据进行整合、进制转换、空载值修正以及有效值提取等操作,得到有效数据。然后对有效数据提取特征,根据测产传感器检测原理和数据特征,综合上文的分析,最终选择每个通道的极差(R1,R2,R3,R4,R5)、方差(V1,V2,V3,V4,V5)和5个通道辐射强度的积分(C)作为数据集特征,以每次实验棉花的喂入质量作为该条数据的标签。
为增加数据集的抗干扰性,对现有数据集增加伪数据。将得到的200条数据,按照正态分布的方式,以每个数据本身为均值,对每条数据中的每个特征使用相同的种子生成5个随机数据。扩展后,数据集总共有1 200条数据,并按照5∶1的比例划分训练集和验证集,其中训练集1 000条,验证集200条。
3 模型构建和优化
3.1 模型选择和训练
前文所述原始传感器和目前国内的采棉机测产系统普遍采用线性模型进行产量标定,但其抗干扰性和鲁棒性较差,在面对田间复杂的工况有时会出现较大的误差。
而随机森林回归模型有着较好降低泛化误差和抗过拟合的性能[22],且在其它农作物测产中有实际应用[23]。因此本文尝试使用该种模型进行产量标定,将前文所建立的训练集数据分别进行线性拟合和随机森林回归(RFR)模型训练,并用验证集检测模型效果。表1为2种模型在验证集上前25个样本的检测结果和残差。图8为两种模型的对角误差图。
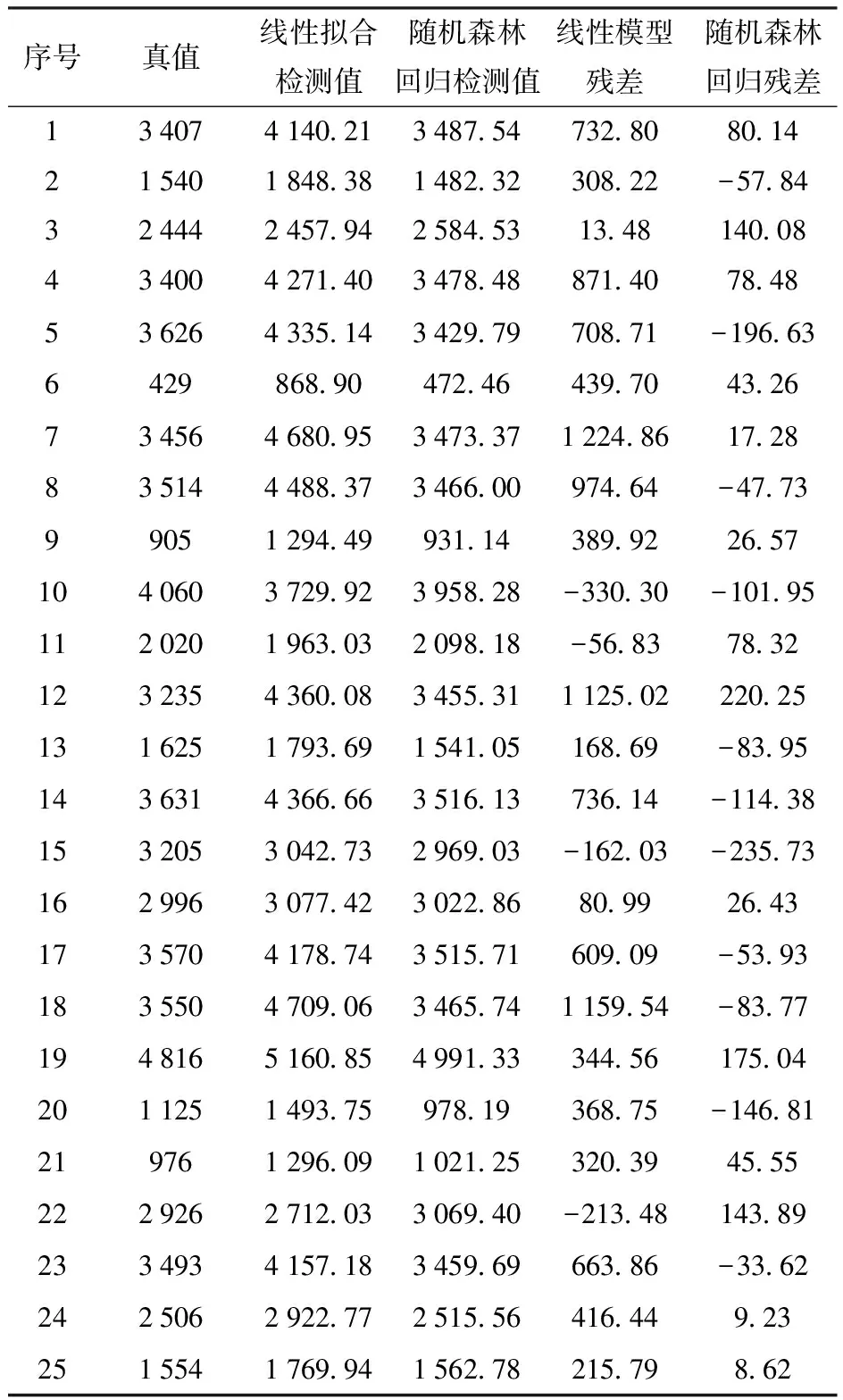
表1 模型检测值和残差
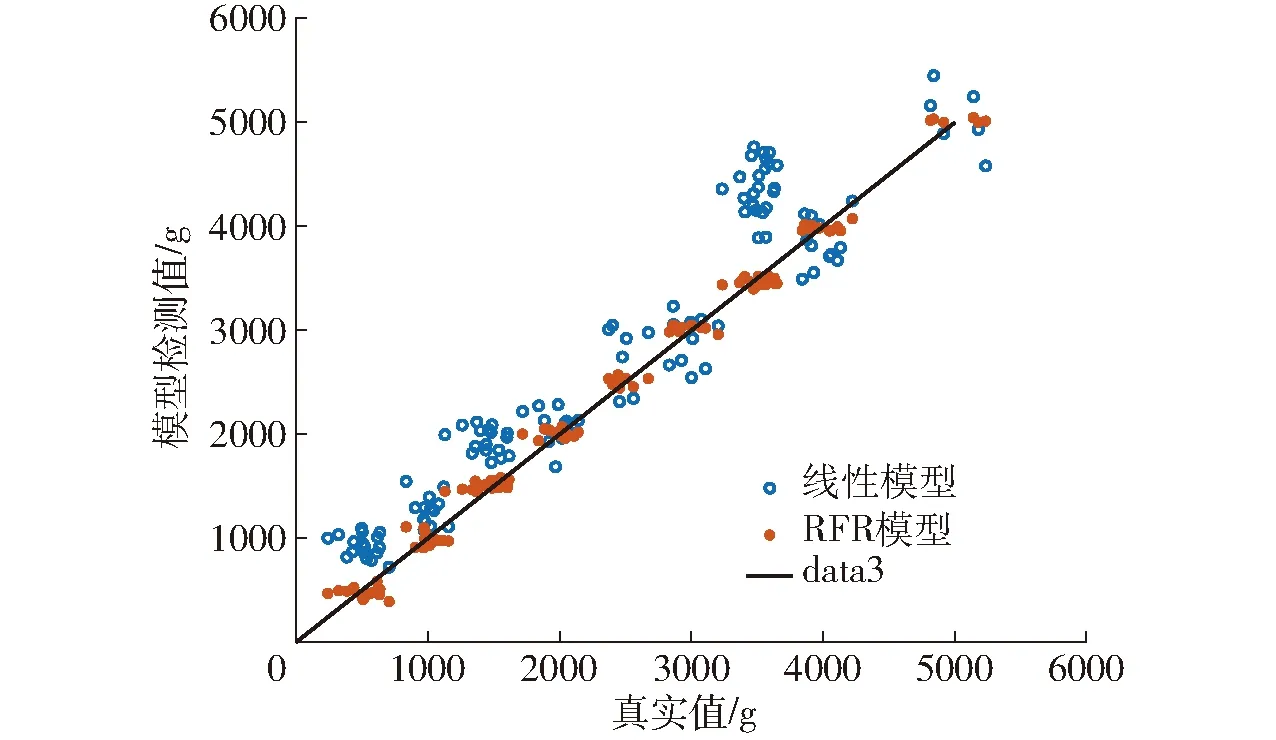
图8 两种模型对角误差
通过图8和表1可以明显看出,在验证集上,RFR模型检测的残差值普遍小于线性模型的检测结果,且在线性模型检测结果在3 500 g附近时有较大误差;RFR模型的预测值比线性模型得到的预测值更加靠近0误差对角线,且随着棉花质量的增大,线性模型的检测值相距0误差线的距离更远,离散程度更高。综合分析可能是棉花质量的增大,实验中的干扰信息增加,线性模型不能很好地区分干扰和有效信息,而使检测值误差增大。两种模型综合评价指标如表2所示。

表2 模型检测结果
综上,本文选择随机森林回归模型作为本传感器的标定模型,并进行后续的研究。
3.2 麻雀优化算法
文献[24]指出随机森林回归模型中,决策树数量和树木深度对最终的预测精度有重要影响。但决策树的个数和深度一般为默认参数设置或人为指定,有很强的主观性,不能在应对不同的应用场景时合理改变。
麻雀优化算法(SSA)[25]是一种基于麻雀觅食和反觅食行为理论启发式算法,使用该算法优化时,具有调整参数少,从开始就能快速收敛的特性。因此,本文采用SSA优化算法对RFR模型的树木棵数和深度进行优化。
在一个麻雀种群中,分为发现者和追随者两组,发现者拥有较好的适应度,为整个种群寻找更好的觅食区域和方向,追随者利用发现者寻找食物。且当负责警示的麻雀发现危险,即大于所设定的安全阈值,发现者将整个种群引向安全地带。
在优化中,麻雀位置表示为
(3)
式中q——种群内麻雀个数
d——需要优化的维数
发现者位置更新式为
(4)
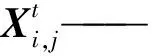
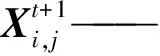
t——当前迭代次数
I——最大迭代次数
a——在(0,1)区间的随机数
Q——正态分布随机数
B——1×d矩阵,其中每个元素都是1
G——预警值V——安全阈值
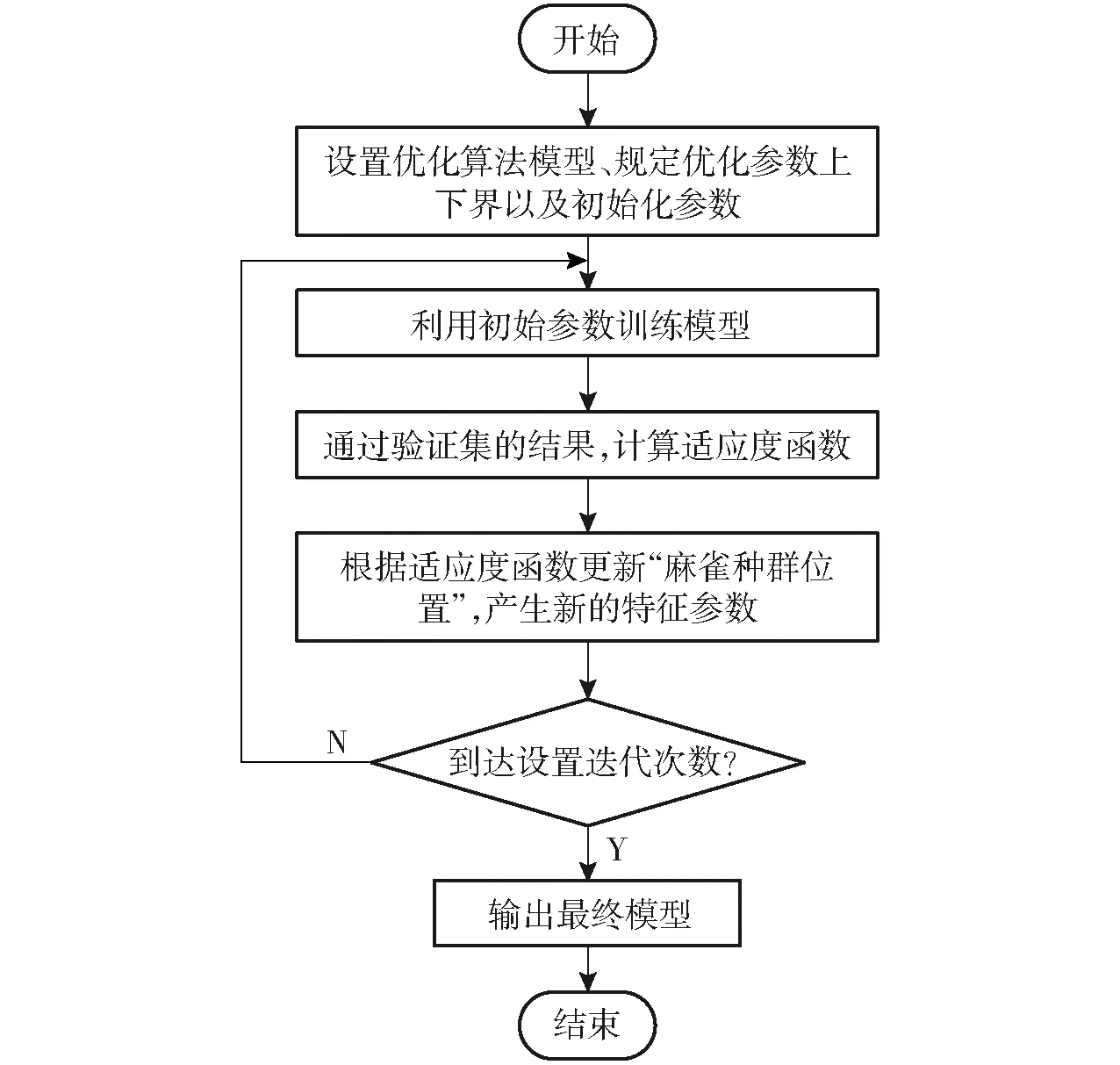
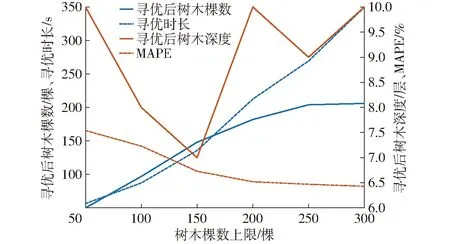
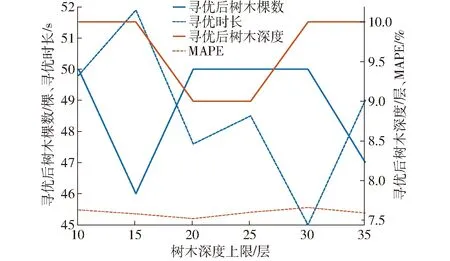
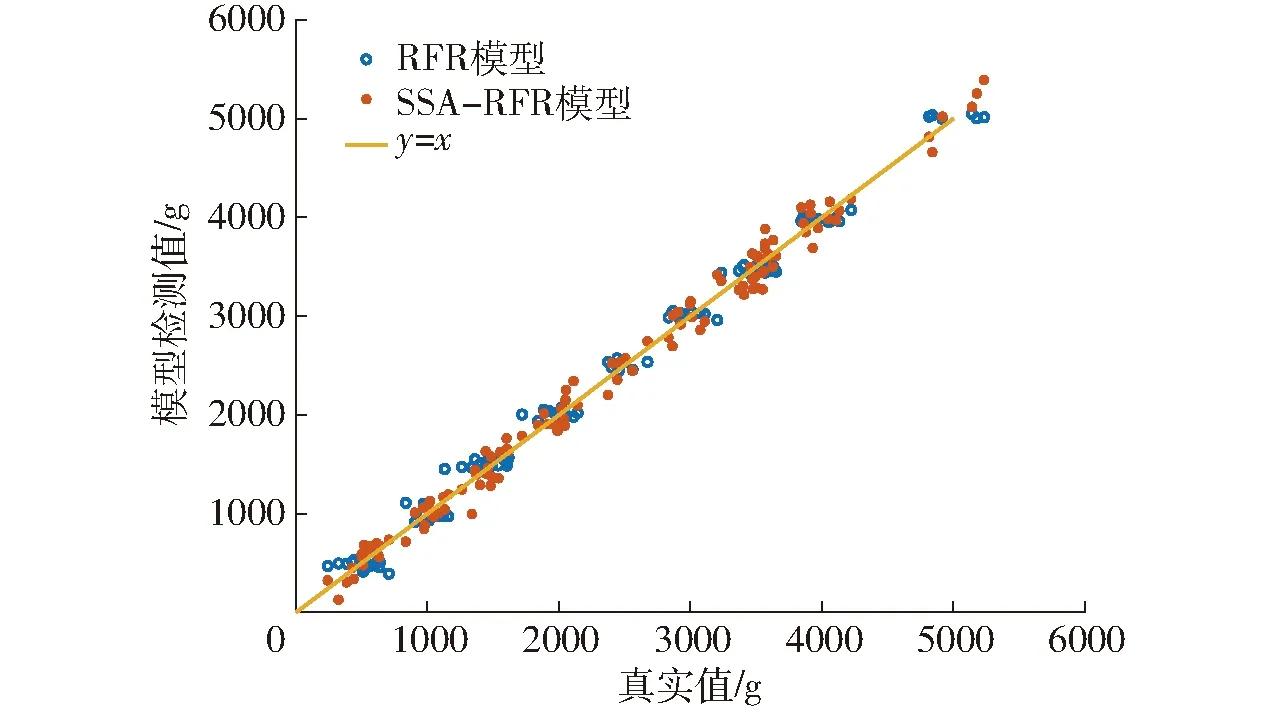
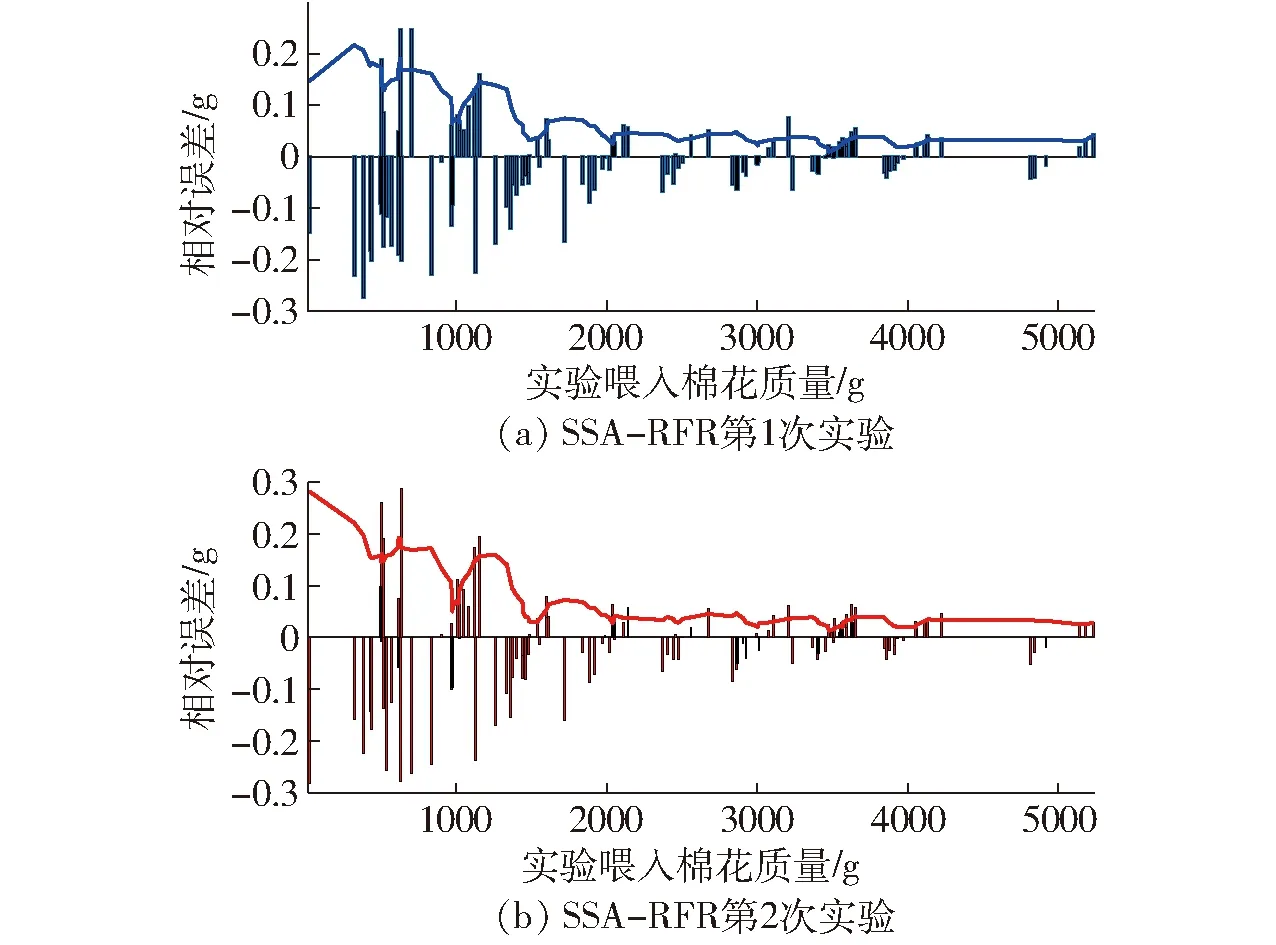
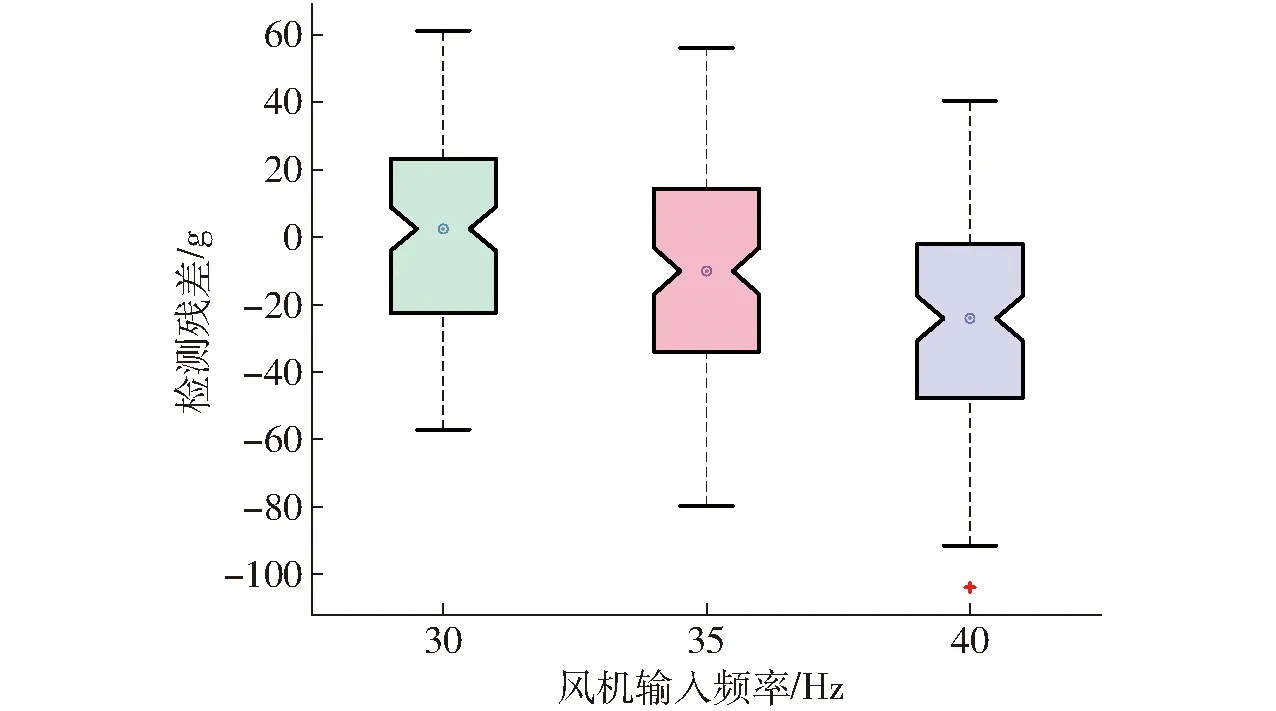
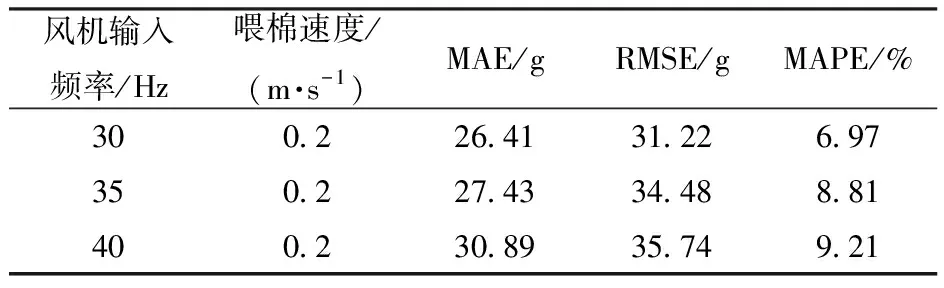
当G 追随者位置更新式为 (5) 警示者一般占整个种群的10%~20%,其位置更新式为 (6) β——服从N(0,1)分布的随机值 K1——麻雀种群的移动方向,在[-1,1]内 ε——小值常数,防止分母为0 fi——第i只麻雀的适应度 fb——当前麻雀种群的全局最佳适应度 fw——当前麻雀种群的全局最差适应度 通过每一次迭代所计算得到的适应度函数,不断改变麻雀种群中发现者和追随者的位置,最终寻得最优参数。 本文通过应用麻雀优化算法对随机森林回归模型的树木棵数和树木深度进行优化,并选择均方误差为适应度函数 (7) 式中s——验证集内数据数量 ms——实验喂入的棉花质量,g 根据前文对麻雀优化算法的叙述,可以设计得到SSA-RFR工作的流程图,如图9所示。 图9 SSA-RFR算法流程图 在设置优化算法参数时,因麻雀优化算法有收敛速度快的特性,迭代次数取10;优化参数分别为随机森林回归的树木棵数和树木深度,其范围(5,50)棵和(2,10)层;预警者比例按照常规取0.2,安全值取为0.6。 SSA进化收敛曲线如图10所示。可以看到,通过10次寻优迭代,麻雀种群适应度有所下降,且在前5次已经达到最优。经过优化的参数选择为50棵决策树,深度为7层。 上述实验可以看到,通过麻雀算法找到的最优超参数是在提前规定好的上下界范围内的,有一定局限性。在保持数据集不变的情况下,对2个寻优参数控制变量,不断改变其上界,使其在保证准确性的前提下,限制运算复杂程度,节省运算成本,选择最优的参数。 在树木深度不变的情况下,树木棵数上限每次增加50棵,进行6次实验,每次实验的搜索时间成本和在验证集的检测准确率如图11所示。 图11 树木棵数范围对寻优影响 在树木棵数不变的情况下,树木深度上限每次增加5,进行6次实验,每次实验的搜索时间成本和验证集的检测准确率如图12所示。 图12 树木深度对寻优影响 在保持树木建模深度不变时,随着树木棵数上限的增加,最优树木棵数和寻优时长都在增加,但真实值和检测值的平均绝对百分比误差在减小。在上限到达200棵以后,明显看出运算成本继续增加,但平均绝对百分比误差几乎不再减小,此时再增大搜索上限收益较低。当保持树木棵数不变时,增加树木深度上限,各评价参数只在一定范围内波动,并无明显变化趋势,说明树木深度的上限选为10层时即满足最优。 经过上述分析得到,最终选择树棵数上限为250棵,深度上限为10层。最终优化参数为206棵决策树,深度为10层,以此参数训练后的随机森林回归模型,作为最终传感器的标定模型。优化后对模型验证,结果的决定系数R2为0.99,平均绝对误差(MAE)为24.69 g,平均绝对百分比误差(MAPE)为6.34%,准确率较随机森林回归原始模型有提高,且运算成本相差不大。寻优参数范围优化前后的模型在相同验证集上的表现如图13所示。可以看出,参数优化后的模型的检测值更加集中于y=x的0误差线上,说明参数优化在一定程度上提升检测准确性。 图13 模型优化前后检测值对比 为验证本文所改进的传感器及其模型检测效果,进行采棉机台架实验验证。实验台架仍采用前文所述的台架,如图14所示。 图14 实验台架 台架可以通过变频器输出改变输棉管道内风机风速,通过控制电机改变喂棉速度。为进一步验证模型检测精确度,并模拟田间复杂的作业环境,本文通过重复验证实验和不同风机风速实验来对传感器检测效果进行测试。 每种工况进行一组实验,每组120次。各组实验内的每次实验棉花质量对应相同,棉花质量在实验前0~5 500 g的范围内随机生成,在每次实验前使用电子秤称量所需质量的棉花。完成实验和数据采集后,使用和2.3节相同的方法对数据进行预处理并提取数据特征,并标注每次实验的真值。 为验证改进后的传感器和检测模型的性能是否稳定,先在同训练集相同的实验条件下进行重复验证实验。 共进行2组实验,设置喂棉速度为0.2 m/s,风机输入频率为30 Hz,按照提前确定的质量进行实验。两组实验数据预处理后,将实验数据输入前文训练好的模型后,输出检测结果。 计算2组实验检测值的相对误差,并将结果按照每次实验对应的喂棉质量从低到高进行排列后,得到相对误差直方图和相对误差绝对值趋势曲线,如图15所示。在前25次实验,喂入棉花质量小于1 250 g时,误差大多数为负值,即检测结果偏小,对于此现象,可能是由于传感器的检测通道之间存在间隔,较小的棉花喂入量使棉花可能从间隔处流经,没有使辐射减弱,导致丢失产量信息。还可以看到随着实验棉花质量的增加,检测值的相对误差呈现减小趋势,且最后稳定在5%附近,符合实际生产的应用。 图15 检测值相对误差 对2组实验检测结果进行评价,2组实验的平均绝对误差(MAE)分别为24.08、22.24 g,平均绝对百分比误差(MAPE)为6.52%和6.02%。实验结果与验证集数据结果基本吻合,说明该传感器的性能稳定,可复现检测结果。 为检验采棉机在田间工作时风机风速改变对检测结果的影响,通过改变变频器的输出频率而调节风机风速,3组实验分别设置3种不同的变频器输出频率为30、35、40 Hz,每次实验的喂棉时间5 s保持不变。 不同风速下的检测值残差箱线图如图16所示。前2种风速下的检测结果残差中心线基本在0附近波动。但可以观察出,随着风速增加,检测结果的残差有向负值变化的趋势,尤其是风机输入频率为40 Hz时,该现象更为明显。对于该现象,可能是由于传感器采样频率不高,但随着风速增加,棉花经过测产传感器时间变短,导致一些棉花信息漏采,而出现检测值较真实值偏小的现象。 图16 不同风速下检测值残差箱线图 还可以看出,随着风速增大,残差的分布也越来越分散,且风速越大,残差极大、极小值也越突出,但从误差绝对值看,最大绝对误差为96.58 g,基本符合检测要求。 对3种风速下的检测结果进行指标评价,结果如表3所示。在喂棉速度不变的情况下,风机输入频率为40 Hz时平均检测误差最大,为9.21%;3种风速下平均检测误差8.33%,检测结果基本符合预期。 表3 不同风机风速下检测结果 (1)对现有采棉机测产传感器存在的问题进行优化,分别对其结构和封装材料进行改进,并重新选型了光传感器,增加可变电流控制模块等。 (2)针对在检测模型时不能很好地应对田间复杂环境的问题,本文尝试随机森林回归模型,在分析其检测表现后,提出麻雀算法优化的随机森林回归模型。最后通过验证表明,该模型决定系数R2为0.99,在测试集的平均绝对百分比误差(MAPE)为6.34%。 (3)台架实验表明,改进后的传感器和检测算法稳定性较好;且在不同风速下,最大误差9.21%,平均误差8.33%,检测效果良好,说明改进后的传感器和检测方法能满足采棉机田间作业时的监测要求。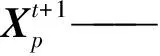
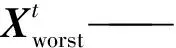
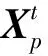
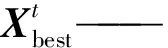
3.3 优化模型训练
3.4 参数调试
4 实验验证
4.1 台架实验

4.2 重复验证实验
4.3 不同风机风速下检测实验
5 结论
