实尺度船用推力轴承动态参数识别方法研究

胡泽超，施 亮

（海军工程大学a.振动与噪声研究所；b.船舶振动噪声重点实验室,武汉 430033）

0 引 言

在不均匀伴流场作用下，螺旋桨周期性运转产生的脉动激励力是船舶在中低速航行时的主要噪声源。该纵向力经过推力轴承传递至船体，会激发推进轴系和壳体的振动以及降低船舶的声学性能。推力轴承是桨-轴-船体振动传递路径上的关键一环，其动刚度识别对于推进系统纵向振动传递特性的分析具有决定性的影响。

目前对于推力轴承动刚度的测试方法，国内外学者已进行了深入的研究。文献[1-3]提出了可倾瓦径向滑动轴承油膜动态参数的测试方法，根据试验测得轴承振动的绝对和相对位移信号可估算油膜的动特性系数，但此法不适用于输入信号与响应信号存在相位差的桨轴系统。2002 年，Pan 等[4]搭建了桨轴系统缩比试验台架，针对推进轴系纵向振动主动控制力需求，进行了轴系振动响应和推力轴承动刚度的测量，实验结果表明：推力轴承动刚度在0～100 Hz低频范围内随频率变化明显，且随螺旋桨转速和推力的变化较大，并指出主动控制系统必须考虑推力轴承刚度的非线性因素。2011年，谢基榕等[5]在轴系与推力轴承脱离的条件下，单独对实船推力轴承的纵向动刚度进行了测试，基于试验分析结果估算了系统的一阶固有频率和推力轴承基座的视在质量，对轴系子系统的刚度计算模型进行了验证。2013年，Lu等[6]认为推力轴承存在一些难以确定的非线性因素，试验研究几乎是唯一能准确识别推力轴承纵向动刚度的方法。2014年，张青雷等[7]利用仿真及实验的方法研究了扰动频率对可倾瓦推力轴承油膜动刚度的影响趋势，结果表明激励频率对油膜的刚度和阻尼的响应幅度基本不随转速或载荷的改变而改变，局限性在于扰动分析频率跨度过大，所得结论对于轴系低频段振动无参考价值。2015 年，俞强等[8]利用锤击法模拟螺旋桨宽带激励，在主机不工作的条件下测量了螺旋桨至推力轴承基座的振动传递函数，但测试结果与轴系旋转状态下的推力轴承动刚度存在区别。2016 年，Wang 等[9]采用锤击法测量了不同推力和转速工况下可倾瓦推力轴承的油膜刚度，结果表明油膜刚度的量级为1000 kN/mm，当推力在30 kN 以内时，理论分析与试验结果相差不超过7%，但随着推力的增加，误差逐渐增大。2017 年，朱鸿等[10]搭建了桨轴缩比实验台，对推力轴承油膜刚度与综合支承刚度进行了测量，结果表明：推力轴承综合支承刚度随着激励频率升高而下降；油膜刚度随转速升高而呈指数衰减，在转速一定时油膜刚度与扰动频率无关，刚度量级为100 kN/mm；在100 Hz以内频段，综合支承刚度与油膜刚度幅值近似相等。试验方法与结果具有一定的参考意义，但与实船级别的推力轴承动态参数特性仍有差别。

综上所述，目前对于推力轴承动刚度的识别方法，国内外学者已进行了深入的研究，但研究对象大多为桨轴系统的缩比模型，测试数据与实船模型存在较大差别，可参考价值不大。为分析桨-轴-船体系统的振动传递特性，必须准确识别不同工况下实船推力轴承的动态特性参数。本文依托实验室艉舱推进轴系平台，采用激振器法测量常用工况下推力轴承的纵向动刚度参数，分析螺旋桨传递至船体基座的振动响应特性及推力轴承非线性的影响，为后续建立桨-轴-船体系统动态设计方法提供分析基础。

1 试验平台组成

如图1 所示，实验室搭建了1:1 实船艉部舱段模型试验平台，主要由推进主机、推进轴系、水润滑径向轴承、推力轴承、高弹联轴器、船体基座、船体耐压壳及配套的冷却润滑辅助系统等组成。目前实验室舱段采用米歇尔式推力轴承，主要由推力轴、推力瓦块、支撑结构、径向轴承、平衡块、套环和壳体等组成，其瓦块数为8，瓦块内径为120 mm、外径为166.5 mm，轴段质量为3 t，润滑形式为油润滑，结构示意图见图2。

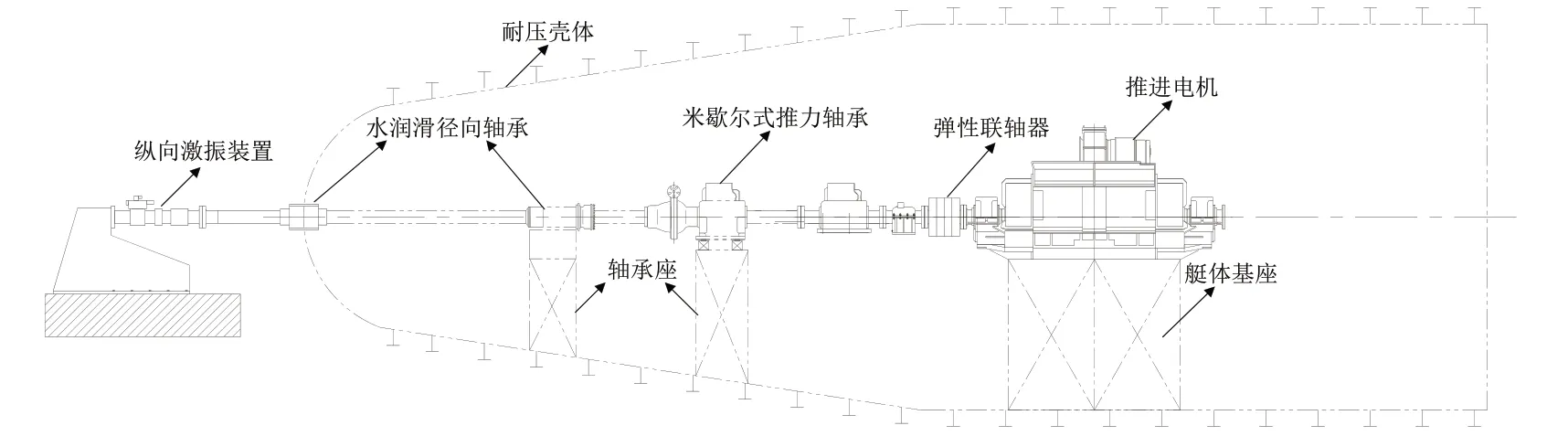
图1 船体艉部结构试验平台Fig.1 Test bench of submarine stern cabin

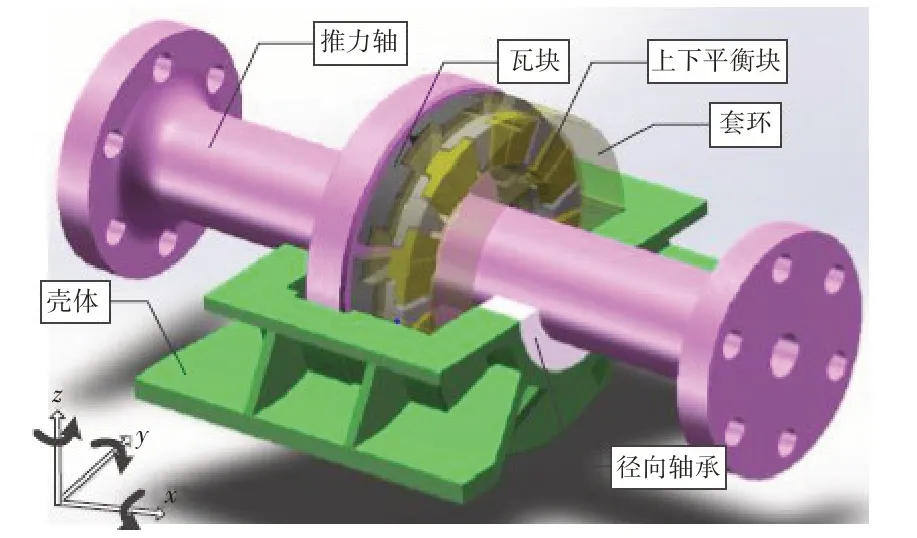
图2 推力轴承结构示意图Fig.2 Structure diagram of the thrust bearing

为顺利开展实船安装状态下推力轴承纵向动刚度测试，搭建了一套专用的测试系统，主要包括轴系纵向激振装置、位移传感器、加速度传感器、力传感器及BK 测试软硬件等。相较于电磁式激振器，液压伺服式激振器具有输出载荷大、控制精度高等优点，因此为了实现较大轴系纵向载荷输出以模拟螺旋桨不同工况下的激励特性，实验室采用如图3 所示的液压伺服加载系统，最大可输出200 kN 静推力和幅值为20 kN 的动态力。

图3 轴系纵向加载装置Fig.3 Shafting longitudinal excitation device

推力轴承实船安装环境见图4，位移传感器布置于如图5 所示的推力轴承附近轴肩处，用以监测轴系相对于推力轴承的振动；加速度传感器用于测量轴承座的绝对振动；力传感器与加载装置串联，用以监测纵向加载装置施加的动态载荷。

图4 推力轴承实船安装环境Fig.4 Installation environment of thrust bearing

图5 位移传感器安装位置Fig.5 Installation position of displacement sensors

2 推力和转速的影响研究

推力轴承油膜刚度随转速、推力变化较大，为准确获得桨-轴-船体的振动传递特性，需要确定不同工况下推进系统的动刚度参数，为下一章推力轴承动刚度的识别方法研究提供试验支撑。如表1 所示，设计了共计400 余种不同推力和转速组合工况，并测量了螺旋桨至推力轴承基座的纵向振动传递函数。图6 和图7 仅给出部分组合工况下推进系统动刚度的变化趋势。图6 为螺旋桨静推力为80 kN 条件下推进系统动刚度随主机转速的变化曲线，图7为主机转速为120 r/min时推进系统动刚度随螺旋桨静推力的变化曲线。

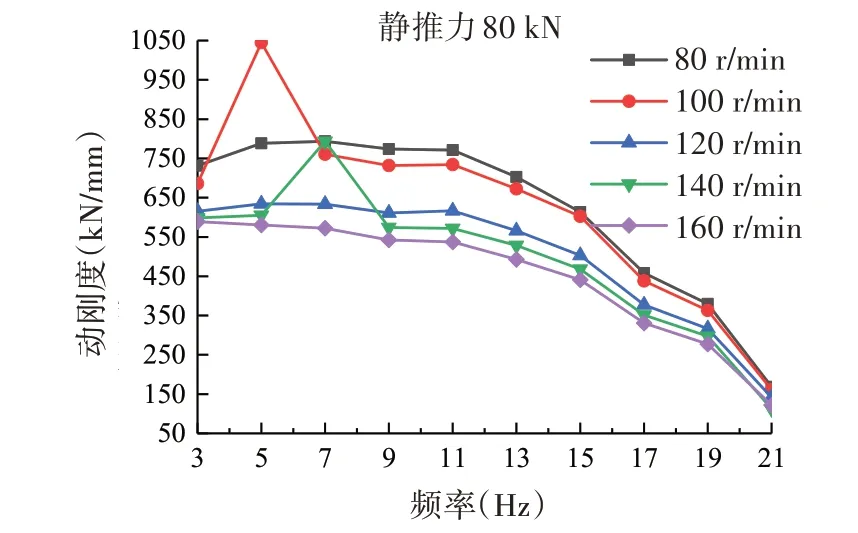
图6 动刚度随转速变化趋势Fig.6 Dynamic stiffness varying with shaft speed

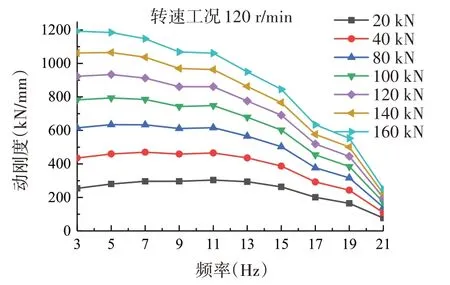
图7 动刚度随推力变化趋势Fig.7 Dynamic stiffness varying with thrust

由图6和图7可得出以下结论：（1）在给定静推力、扰动频率的条件下，推力轴承动刚度随转速的增加而减小；（2）在给定转速、扰动频率的条件下，推力轴承动刚度随螺旋桨静推力的增大而增大；（3）在给定静推力、转速的条件下，推力轴承动刚度随扰动频率的增大而减小，当扰动频率达到21 Hz 附近时，转速对动刚度影响不大，推测推进系统在21 Hz 附近存在共振峰；（4）在转速100 r/min扰动频率5 Hz处以及转速140 r/min扰动频率7 Hz处推力轴承动刚度数值出现异常，这是由于受到了3倍轴频的影响。

3 推力轴承动态参数识别方法研究

3.1 测试方法及原理

螺旋桨纵向脉动力通过推进轴、推力轴承和轴承座传递至船体，由于推力轴承纵向刚度远小于船体且二者之间为串联关系，可认为桨-轴-船体系统的纵向总刚度与推力系统的纵向刚度近似相等。为模拟船体自由边界条件，艉舱耐压壳体由16 个300 kN 型额定载荷为30 t、固有频率为3.5 Hz 的气囊弹性支撑。考虑轴承基座的视在质量对推力轴承动刚度的影响，可将桨-轴-船体系统简化为图8所示的两自由度系统。图中螺旋桨纵向激励力为FP，桨轴系统的质量为M1，推力轴承、基座和船体的总质量为M2，推力轴承的静刚度和阻尼分别为KH、CH，气囊的静刚度和阻尼分别为KS、CS，x1、x2分别表示推进轴、轴承基座的纵向位移，轴承的动刚度可表示为=KH+jωCH，式中ω= 2πf，f为扰动频率。

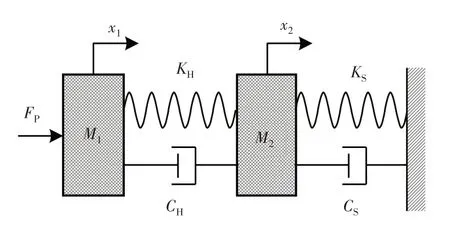
图8 桨-轴-船体简化模型Fig.8 Simplified model of propeller-shaft-hull

根据图8所示的桨-轴-船体系统两自由度简化模型，由达朗贝尔定理可知

令H1(ω) =(X1(ω) -X2(ω))/FP(ω)、H2(ω) =X2(ω)/FP(ω)，则式（1）可表示为

令P(ω) = Re()，Q(ω) = Im()，推力轴承的静刚度和阻尼可分别表示为

设KZ和KZC分别表示桨-轴-船体系统的纵向总体动刚度和推力轴承基座动刚度，由于推力轴承与轴承座刚度上为串联关系，其刚度参数可表示为

实验中需测量螺旋桨至推进轴、推力轴承基座的传递函数H1(ω)、H2(ω)，然后根据式（2）与式（6）可计算得到推力轴承及其基座的动刚度参数。

3.2 试验结果分析

液压加载装置配套的伺服控制系统可输出100 Hz 以内的单频正弦信号和白噪声信号，最大动态力幅值为20 kN。本节分别采用单频激励法和随机激励法测量主机转速为70 r/min、推力为40 kN工况下的传递函数H1(ω)、H2(ω)，两种方法可相互验证。其中激振器采用单频正弦激励力作为输入，动态力幅值为1 kN，频率范围5～99 Hz、间隔2 Hz；随机激励法采用幅值为1 kN、频率范围为5～100 Hz的白噪声激励作为输入，稳态工况下传递函数的测试结果如图9和图10所示。

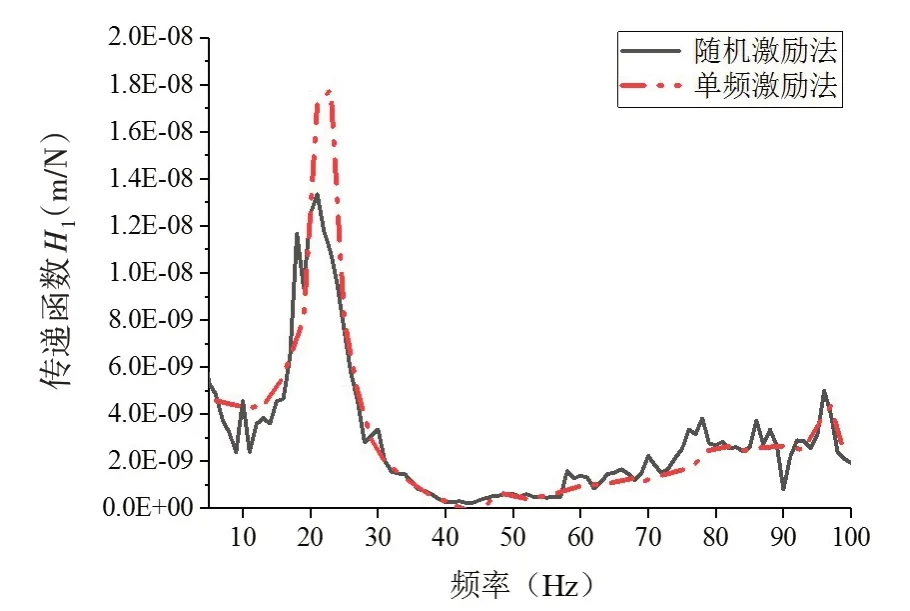
图9 传递函数H1(ω)Fig.9 Transfer function H1(ω)

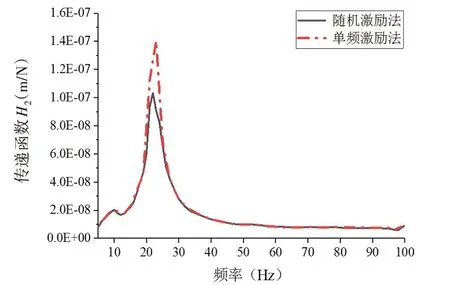
图10 传递函数H2(ω)Fig.10 Transfer function H2(ω)

由图可知，两种测试方法得到的传递函数曲线变化趋势相同，但单频激励法需测试工况较多，且频率分辨率较低，忽略了推进系统的一些重要细节特征。而随机激励法不仅能够获得更好的测试结果，还能简化试验过程，因此应采用随机激励法进行推力轴承的动刚度测试。图中传递函数H1(ω)和H2(ω)均在21 Hz附近出现了峰值，这是由于该处为推进系统的一阶纵荡模态。

根据测试结果，通过式（4）～（6）可以分别计算出推力轴承、轴承基座以及推进系统的纵向动刚度，计算结果如图11所示。

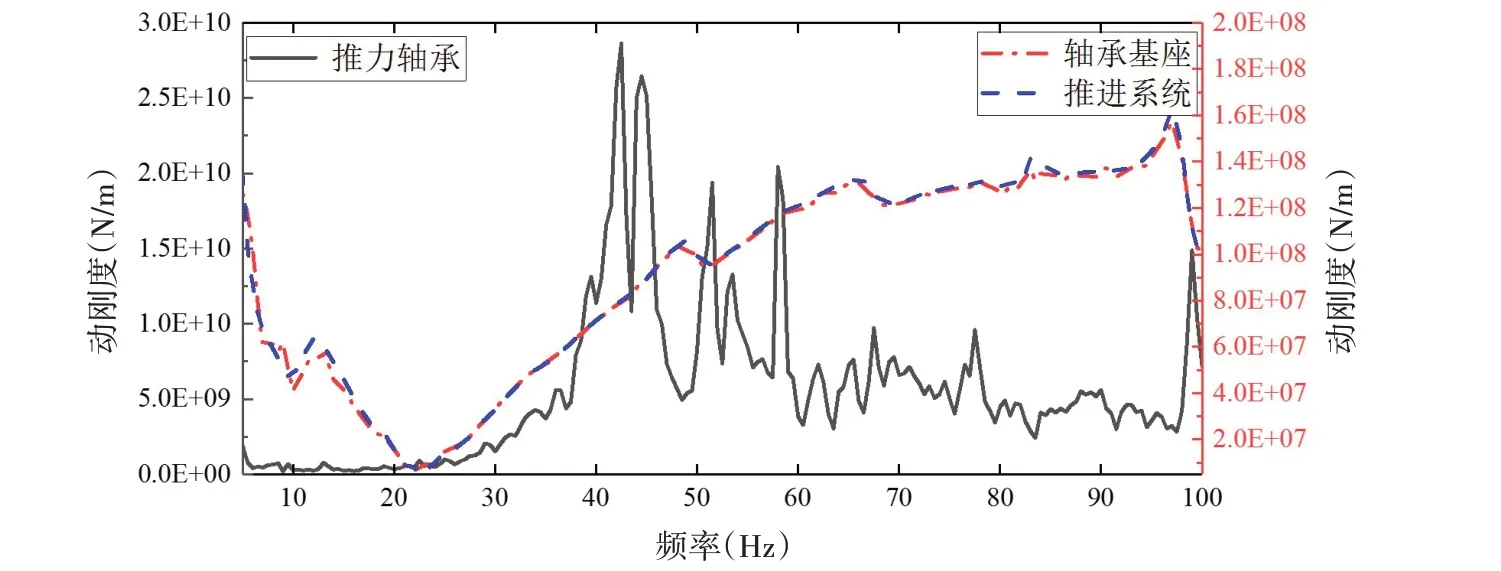
图11 动刚度测试结果Fig.11 Test results of dynamic stiffness

总体来看，推力轴承动刚度呈现出复杂的非线性特征，而轴承基座与推进系统动刚度曲线变化趋势基本一致，均随扰动频率的增加而增大。由于21 Hz 附近存在推进系统的一阶纵荡模态，轴承基座的动刚度较小。在5～100 Hz 范围内，推力轴承动刚度约为109～1010N/m，而基座的动刚度仅为107～108N/m，由于推力轴承与轴承基座刚度上为串联关系，推进系统的纵向总刚度由基座的动刚度决定。由于推力轴承基座高约2 m，其一端焊接在船体耐压壳体上，对于径向尺度相对较小的船体结构可视其为一根长直的悬臂梁；轴承座另一端与推力轴承相接，在悬臂梁受到纵向激励时，轴承端的振动较大，导致传递函数H2(ω)偏大。因此，为降低螺旋桨纵向脉动力传递至船体的振动能量，设计时应尽可能缩短推力轴承基座的高度以提高其纵向动刚度。

4 推力轴承动态参数对振动传递特性的影响分析

在计算桨-轴-船体的振动传递特性时，传统方法通常是将推力轴承的刚度视为恒定值，其取值范围一般处于107～1011N/m之间（为便于比较，本章取5.0×109N/m）。为分析推力轴承动刚度非线性特性对推进系统振动传递特性的影响，基于实验室实尺度船体艉部舱段模型，建立了如图12 所示的桨-轴-船体有限元简化模型，分别将传统方法和本文测试方法获得的动刚度参数作为数值分析模型的输入，在螺旋桨处施加10～100 Hz纵向单位简谐激励力，计算推力轴承基座处的振动响应曲线，结果如图13所示。

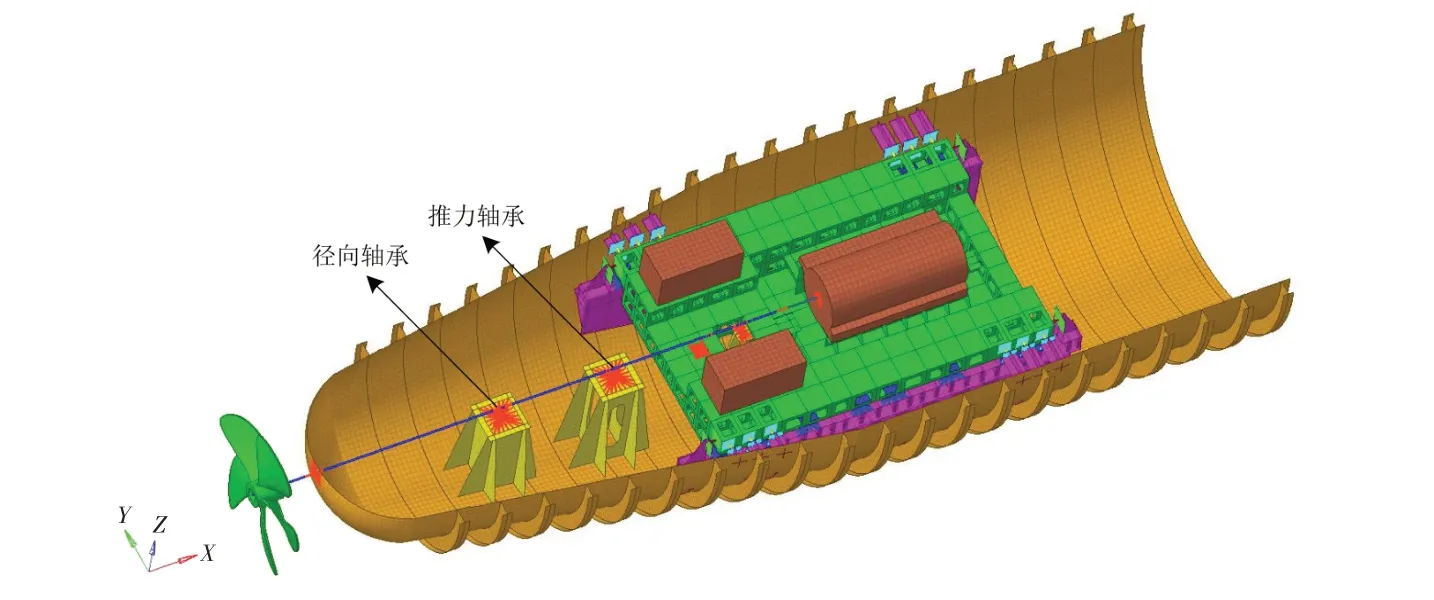
图12 桨-轴-船体数值分析模型Fig.12 Finite element analysis model of propeller-shaft-hull

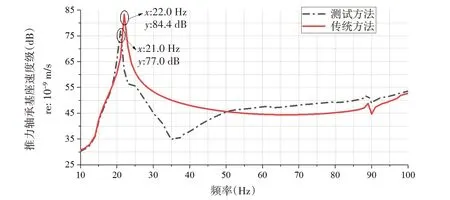
图13 桨-轴-船体纵向振动传递曲线比较Fig.13 Comparison of longitudinal vibration transmission curves of propeller-shaft-hull

结果表明，若按照传统方法将推力轴承动刚度参数视为恒定值，则计算得到的一阶纵荡模态频率偏高，且振动响应峰值比实测值高出7.4 dB，存在较大误差。因此为提高计算精度，在利用数值分析法估算桨-轴-船体的振动传递特性前，获取准确的推力轴承动刚度数据尤为重要。

5 结 论

本文建立了桨-轴-船体的解析模型，提出了推力轴承动刚度的测试方法，基于搭建的实船艉舱推进系统试验平台，测量了螺旋桨至推力轴承及其基座的传递函数，识别了安装状态下推力轴承的动刚度。然后建立了桨-轴-船体的数值分析模型，分别将推力轴承动刚度实测值和传统方法中被视为恒定值的推力轴承动刚度作为模型的输入，分析了螺旋桨传递至船体基座的振动响应。本研究得到了以下结论：

（1）在给定静推力、扰动频率的工况下，推力轴承动刚度随转速的增加而减小；在给定转速、扰动频率的工况下，推力轴承动刚度随螺旋桨推力的增大而增大；

（2）为降低螺旋桨纵向脉动力传递至船体的振动能量，设计时应尽可能缩短推力轴承基座的高度以提高其纵向动刚度；

（3）推力轴承动刚度在低频范围内具有较强的非线性，若将其参数视为恒定值，则计算得到的系统一阶纵荡振动响应峰值比实测值高出7.4 dB，存在较大误差。因此在利用数值分析法评估桨-轴-船体的振动传递特性前，获取准确的推力轴承动刚度数据尤为重要。