大型集装箱船舱口角隅高低周复合疲劳寿命预报方法研究

2023-09-22胡育华乐京霞

船舶力学 2023年9期

胡育华，乐京霞

（武汉理工大学船海与能源动力工程学院，武汉 430063）

0 引言

集装箱船由于航速快、装卸效率高、货损少等优点，已经成为国际贸易主要运输工具之一。然而，由于集装箱船具有货舱区域开口大、舷侧宽度窄等特点，使得舱口角隅应力集中现象明显，是疲劳失效的易发和多发部位[1-2]。一般而言，船体结构受到疲劳损伤而失效的形式属于高周疲劳。但在船舶航行遭遇极端海况时，由于角隅处的应力集中，该处应力存在临界甚至超过材料屈服极限的可能，最终引发结构在较少的极端循环载荷下发生低周疲劳破坏。事实上，多次经历恶劣海况的超大型集装箱船，在其服役期间所受的复杂载荷引起的疲劳损伤可视为高低周复合疲劳问题。因此，合理评估船舶舱口角隅疲劳寿命是确保集装箱船舶结构安全可靠性的一项重要工作。

目前，许多学者在船舶舱口角隅的疲劳评估方法方面进行了研究：李旭[3]基于HCSR 和CSR 规范的舱口角隅疲劳评估，提出了舱口角隅设计建议；Chen[4]等用测量的应变数据和记录的裂纹数据对比分析了多种预报舱口角隅疲劳寿命方法的可靠性；Fricke[5]等用各船级社提出的疲劳校核方法校核了某集装箱船舱口围板顶板附近构件的疲劳强度；郭宇龙[6]等通过谱分析方法研究了波激振动现象在船体疲劳问题中的影响；余宏淦[7]等采用断裂力学方法结合简化算法对船舶舱口角隅的疲劳问题进行了研究。部分学者则是重点研究了船体结构的低周疲劳问题：汪丹[8]等对船舶缺口板在应力循环载荷下的低周疲劳问题进行了研究，并重点对累积塑性现象进行了分析，对疲劳裂纹萌生寿命的评估方法提出了建议；袁锐[9]等针对弹塑性计算方法中计算时间长且不易收敛的缺点，给出了基于伪热点应力的疲劳寿命曲线设计方法。还有学者对复合疲劳问题进行了研究：郑鑫[10]等开展了高低周复合载荷条件的疲劳裂纹扩展试验，并提出了复合疲劳损伤指数衰减模型；田纵横[11]等提出了船舶在遭受低频波浪载荷历程中存在高频振动分量，并给出了高频分量对复合损伤的影响规律；宋松[12]等在连续损伤力学的基础上，建立了高低周复合损伤模型，并分析了模型参量对高低周疲劳交互作用的影响。

综上所述，对于高周疲劳或低周疲劳的理论研究较为成熟，在船舶结构安全性评估中存在的问题主要包括三点：一是高周疲劳到低周疲劳是一个逐渐过渡的过程，不应该人为根据经验进行定性分类[13]；二是高周疲劳与低周疲劳的评估指标和衡量标准不同，会导致不同标准下疲劳评估结果相互冲突[14-15]；三是船体结构疲劳性能研究大多是围绕高周疲劳或低周疲劳进行的，很少针对高低周复合疲劳开展。因此本文采用能够统一表征高低周疲劳性能的高低周复合疲劳模型，对集装箱船舱口角隅进行疲劳强度分析，并与基于S-N曲线的疲劳寿命方法进行对比。研究结果可为集装箱船舱口角隅疲劳寿命评估提供参考。

1 船体结构高低周复合疲劳寿命预报方法

1.1 高低周复合疲劳寿命预报模型

对于服役期间所受载荷复杂的结构而言，简单将其疲劳问题归类于高周疲劳或低周疲劳显然不够准确。因此，为了能够更准确地预测角隅结构的疲劳寿命，本文采用高低周复合疲劳寿命预报模型对舱口角隅结构进行疲劳寿命计算。张哲峰[16]等通过对系列合金的高低周疲劳性能与微观损伤机制的研究，提出了能够统一表征高周与低周性能的复合疲劳模型。该模型设定在如图1 所示的三维空间坐标系中，X、Y、Z轴分别为应力幅（Δσ）、应变幅（Δε）与疲劳寿命（Nf），在此坐标系中，不同外载条件下应力-应变响应的滞回环应位于平行于X-Y坐标系的平面上，并依照相应循环寿命分布在Z轴的不同高度；将各滞回环的应力/应变峰值点相连，即可获得一条三维曲线。将该曲线向X-Y坐标系投影，即可得到相应的应力应变曲线；同理，其在X-Z坐标系下的投影为S-N曲线，而在Y-Z坐标系下的投影为ε-N曲线。由此，高低周复合疲劳模型成功将经典力学理论中的S-N曲线、ε-N曲线和应力应变曲线以空间曲线的方式进行了整合。

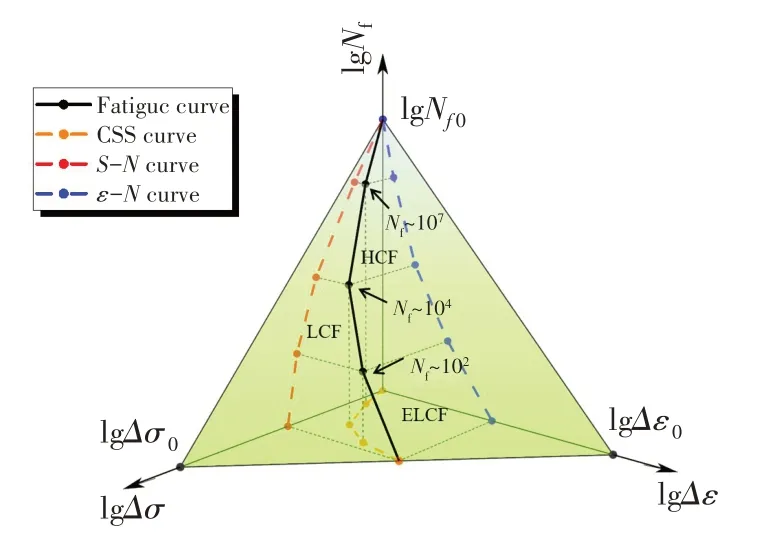
图1 高低周复合疲劳寿命预报模型Fig.1 High-and low-cycle composite fatigue life prediction model

对于常规的金属材料而言，在双对数坐标下，ε-N曲线与S-N曲线的有限寿命段均可近似看作直线；在这种情况下，三坐标轴均为对数坐标时，在一定范围内该空间曲线所在的面可当作空间平面近似处理。在这一假设前提下，该曲线所在面的表达式具有以下基本形式[16]：

式中，Δσ、Δε和Nf分别为应力幅、应变幅和疲劳寿命；lgΔσ、lgΔε和lgNf则分别为空间平面与对数坐标系的三轴交点，为常数项。

式（6）即为高低周复合疲劳模型的损伤形式。

1.2 船体结构高低周复合疲劳计算流程

1.2.1 水动力和结构响应计算

谱分析方法是现今应用较为广泛的船舶与海洋工程结构疲劳寿命计算方法，该方法假定波浪为一个平稳的随机过程，在时间恒定的线性系统变换下，系统输出的结果也应当是一个平稳的随机过程。为了确定船舶舱口角隅的热点应力，首先通过水动力分析和结构响应分析得到单位波高下的全船响应，即响应传递函数。船舶航行过程中的每一个装载工况、航速以及浪向角的组合均可计算出一个单独的响应传递函数，然后将得到的传递函数与波浪谱结合得到热点应力功率谱。最后根据功率谱的0阶谱矩计算得到舱口角隅处的应力水平。

1.2.2 局部应力应变值计算

在船体结构疲劳问题分析中，若想要能够精确预测结构的疲劳寿命，准确获取该部位的应力应变历程是其中的关键。对极端海况所引起的角隅应力水平临界甚至超过屈服强度的情况时，可认为此时角隅结构已经产生了一定程度的塑性变形，此时仅简单使用S-N曲线估算结构的寿命已不合适，因此本文采用高低周复合疲劳模型结合Neuber公式的方法来计算角隅结构的寿命。

Neuber提出理论应力集中系数kt等于应力放大系数kσ和应变放大系数kε的几何平均数：

式中，应力放大系数kσ=σ/s，应变放大系数kε=ε/s。

通过胡克定律，得

式中，kt为理论应力集中系数，s为名义应力，σ为真实应力，ε为真实应变。

而事实上，公式（8）中的ktS本质为理想弹性下应力集中处的应力值。此时，在线弹性有限元分析下可得到结构应力集中处的节点应力值，公式（8）可表达为

再根据Neuber双曲线和循环应力-应变曲线获取两者交点，该点值即为应力集中处的真实应力应变值，可通过下式描述[7]：

式中，σela为理想弹性状态下的应力值，σpla为弹塑性状态下的应力值，E为材料弹性模量，K'为材料循环强度系数，n'为材料循环硬化指数。此时得到的应力应变值即可代入高低周复合疲劳计算公式中使用。

1.2.3 高低周复合疲劳模型建立

在利用高低周复合疲劳计算公式前，需确定公式（6）中的各个参数。本文所用材料为船用高强钢EH36，绘制出Nf=102、Nf=103直至Nf=107下的应力应变响应的滞回曲线，并将各滞回曲线的应力应变峰值点相连，得到了空间坐标系下的一条三维曲线。根据上节所述，将该三维曲线所在面近似处理为空间平面。该空间平面与空间坐标系三轴截距即为公式（6）特征参数，计算值如表1所示。

表1 EH36高低周复合疲劳模型特征参数Tab.1 Characteristic parameters of EH36 3D fatigue model

1.2.4 复合疲劳寿命预报

最后将应力应变值代入上述高低周复合疲劳模型，即可计算结构的疲劳损伤，以80%材料屈服极限为界限分为两种情况：对于低于80%材料屈服极限的应力，应变幅根据线弹性假设计算得到并直接代入式（6）进行计算；对于大于80%材料屈服极限的应力，根据式（10）计算得到弹塑性状态下节点真实的应力应变值，再将该值代入式（6）计算，即可得到高低周复合疲劳模型的损伤度。

上述计算流程如图2所示。

2 集装箱船舱口角隅高低周复合疲劳寿命预报

2.1 计算模型

本节以某大型集装箱船船首与船中处的舱口角隅为研究对象，进行高低周复合疲劳寿命预报。该集装箱船主尺度如表2所示。

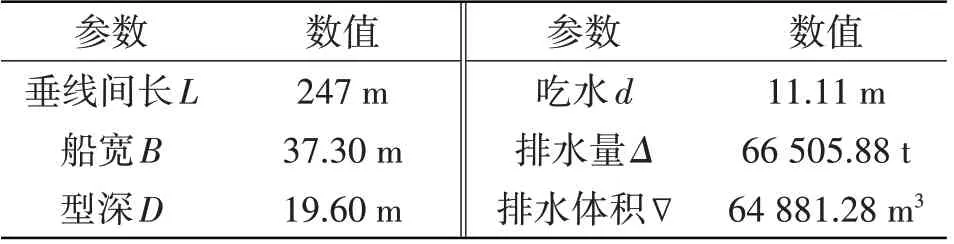
表2 某大型集装箱船主尺度Tab.2 Main dimensions of a large container ship

计算模型包括了水动力计算模型及结构模型。水动力模型包括湿表面模型及质量模型，如图3 所示；质量模型用于统计船舶整体重量、重心分布、回转半径等稳性参数，联合湿表面模型，通过Rankine 源方法计算船舶的三维辐射力及绕射力，从而得到施加在船体的外表面压力。建立结构模型即完整的全船有限元模型，并对角隅结构进行网格细化，如图4 所示，用于计算结构应力响应。

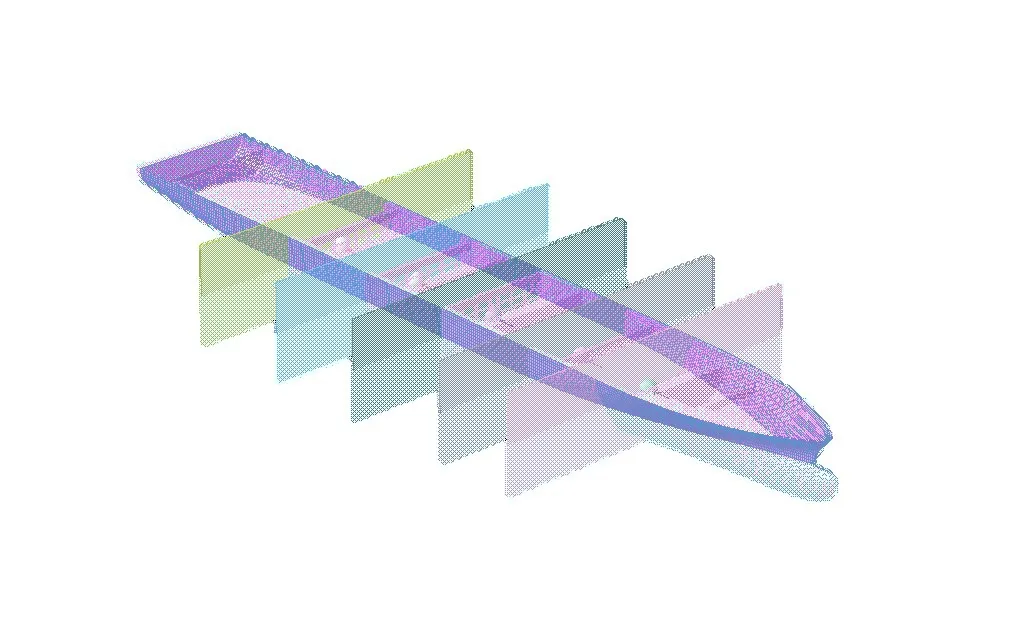
图3 全船水动力模型Fig.3 Ship hydrodynamic model

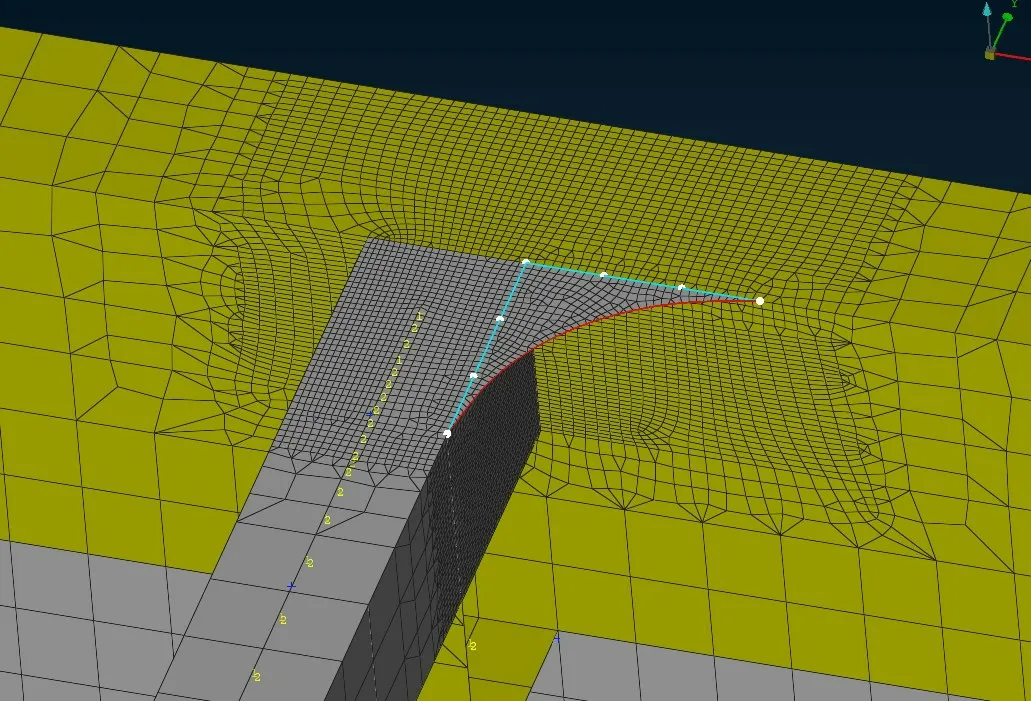
图4 角隅结构局部细化模型Fig.3 Local refinement model of hatch corner

2.2 载荷计算

2.2.1 波浪载荷

本文利用水动力分析软件Sesam，得到船体结构在满载单位波高条件下不同浪向和波浪频率的运动和结构响应幅值算子（response amplitude operator,RAO）。海况资料选取根据CCS《船体结构疲劳强度指南》[17]，计算所取的浪向角应不少于7个，本文选取为0°（迎浪）～180°（随浪），步长间隔为30°，波浪频率范围为0.2～1.8 rad/s（步长0.1 rad/s），每个浪向等概率出现。

2.2.2 质量载荷

质量模型中应能准确模拟集装箱的质量特性（质量、质心及质量分布情况）。为了将集装箱的重力和惯性力有效传递到主船体上，在实际集装箱装载位置上布置质量点，并通过MPC的连接方式连接到船体底座相应位置来加以实现。

2.3 应力传递函数

根据全船结构直接计算结果，本文选取集装箱船中（174 号肋位）与船首（71 号肋位，约为1/4 船长处）剖面处舱口角隅疲劳热点，提取其自由边4 处单元的应力传递函数，单元位置见图5，最大热点应力均在节点4，两处角隅的节点4应力传递函数见图6～7。

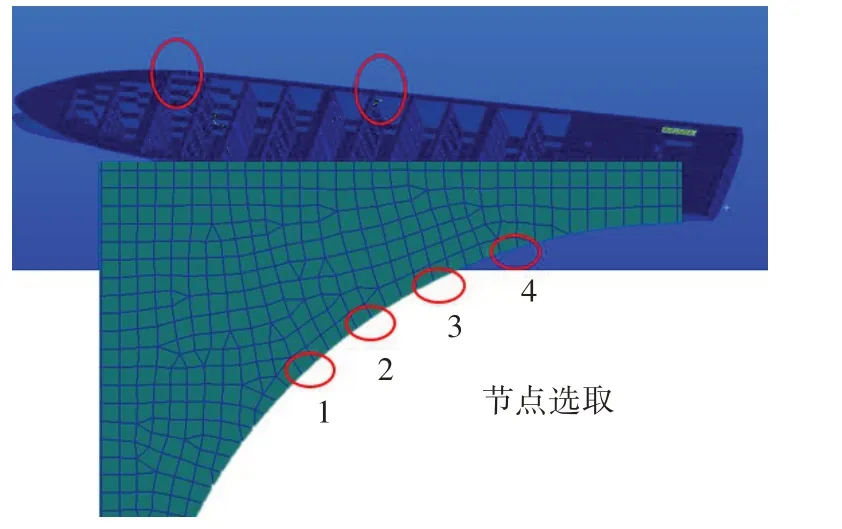
图5 热点应力单元位置Fig.5 Hot spot stress element locations

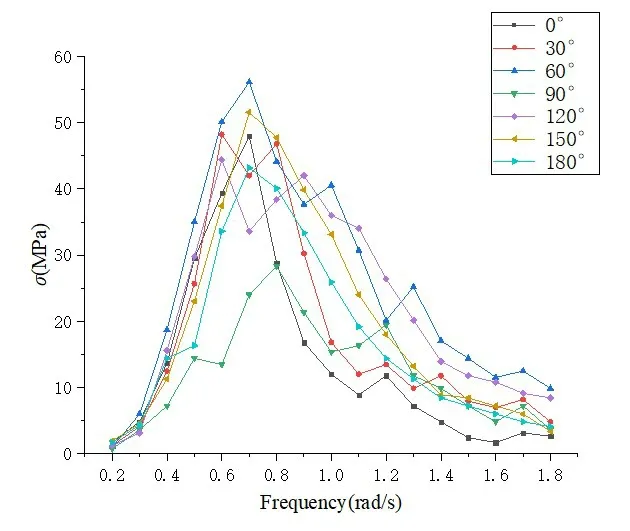
图6 船艏区域节点4的热点应力传递函数Fig.6 Hot spot stress transfer function of Node 4 in ship bow area

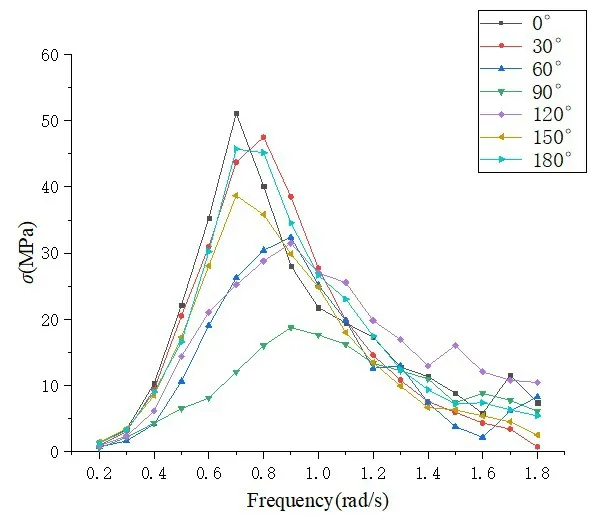
图7 船舯区域节点4的热点应力传递函数Fig.7 Hot spot stress transfer function of Node 4 in midship

2.4 短期预报

由于角隅最大热点应力区域为节点4，因此采用节点4的应力传递函数对波浪散布图中的每个海况进行计算，得到节点的应力谱Sσ，计算公式如下[18]：

式中，Sσ（ω|HS，TZ，θ）为热点应力功率谱密度函数，Hσ（ω|θ）为热点应力传递函数，Sξ（ω|HS，TZ）为波浪谱密度函数。波浪谱密度函数Sξ（ω|HS，TZ）的参数需选取合适的波浪散布图中的数据，本文选取的是全球波浪散布图[19]。

应力功率谱密度函数的第n阶的响应谱矩mn表示为

假设波浪是一个均值为零的平稳高斯过程，那么短期内的船舶响应过程也是一个均值为零的平稳高斯过程。对于窄带响应过程来说，其峰值符合瑞利分布：

式中，m0为响应谱的0阶矩，其等于交变应力过程的方差。当交变应力过程为窄带随机过程时，跨零率约等于峰值率，也就是说每一次跨零对应一个峰值，于是可以认为疲劳计算所需的节点应力范围σ等于应力幅值σa的两倍[20]。

2.5 长期预报

由于船舶的整个航行周期并不是一个平稳的随机过程，因此需要根据波浪的长期统计资料，确定各海况出现的概率，并以一定的加权系数叠加起来获得波浪载荷的长期预报。长期预报下的波浪载荷分布可以表示为

式中，rij为短期海况下跨零率与平均跨零率之比，Pij为第i个海况下第j个浪向角下的航行概率。

2.6 疲劳累积损伤

在确定波浪载荷的长短期预报值后，可根据S-N曲线和线性累计损伤理论得到疲劳累积损伤值。计算公式如下：

式中，a1和m1是S-N曲线中循环次数N≤107时的参数，a2和m2是S-N曲线中循环次数N＞107时的参数，S0是S-N曲线转折点的应力值。

3 角隅疲劳寿命计算与结果对比

根据2.4 节响应谱矩的计算公式，可以求得在一定海况、浪向角度下角隅节点的应力水平。以浪向60°、平均跨零周期为8.5为例，船艏舱口角隅四个节点的热点应力如表3所示。

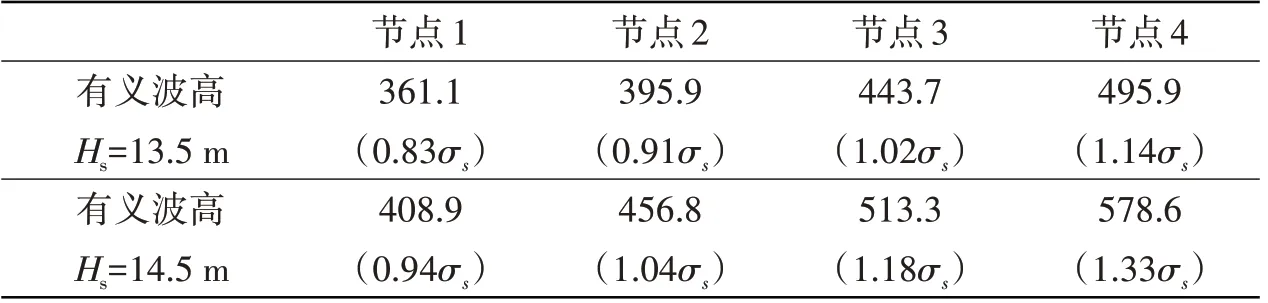
表3 船中角隅区域热点应力幅值(MPa)Tab.3 Hot spot stress amplitude in the corner of the midship(MPa)

该集装箱船舱口角隅材料为船用高强钢EH36 钢，若屈服极限取σs=435 MPa，则在有义波高大于13.5 m 时，其舱口角隅处应力水平超过了0.8σs，最大达到了1.33σs。此时，若用S-N曲线法计算疲劳损伤是无法考虑的，应该采用高低周复合疲劳模型来评估舱口角隅的结构寿命。

定义集装箱舱口角隅的疲劳寿命Tf为

式中，Td为集装箱船设计疲劳寿命，本文取25 年；DT为疲劳总损伤度。表4 给出了船首区域和船中区域两处舱口角隅的高低周复合疲劳寿命计算结果。为了对比，表中同时列出了基于S-N曲线所得到的疲劳寿命预报结果。

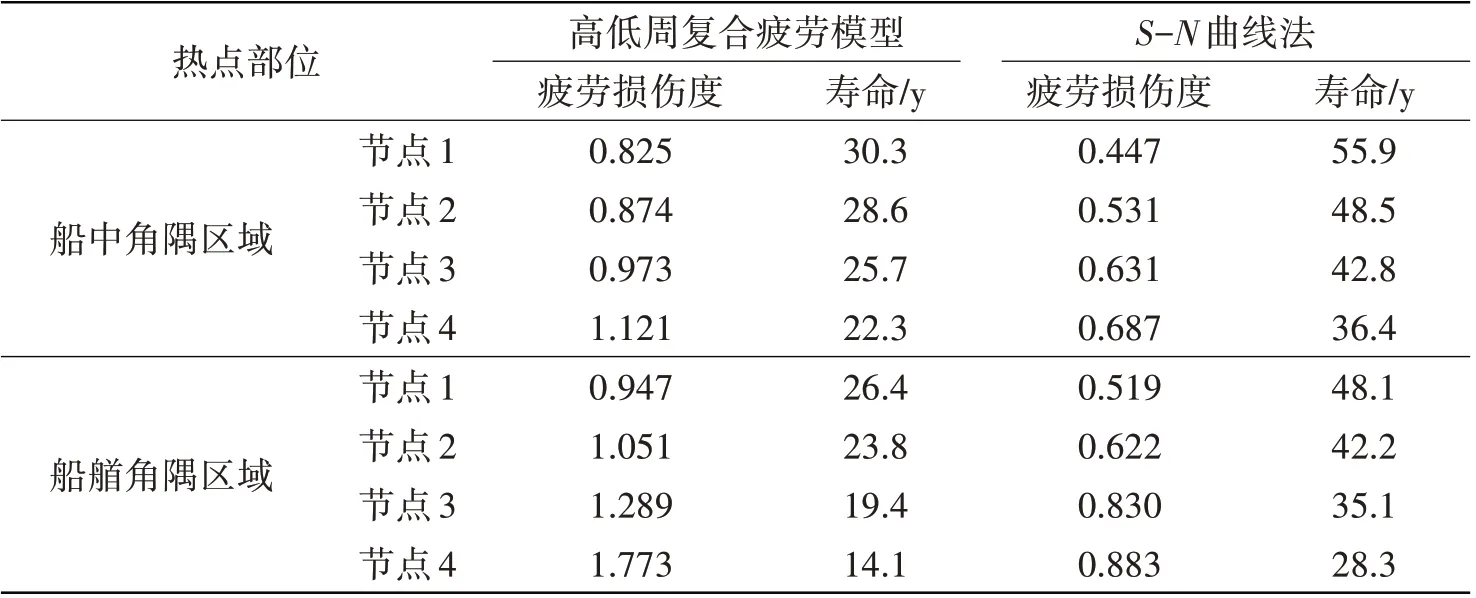
表4 高低周复合疲劳模型与S-N曲线的寿命预报结果对比Tab.4 Comparison of life prediction results between high-low cycle composite fatigue model and S-N curve

从表4 可以看出，高低周复合疲劳模型方法计算的角隅寿命均短于S-N曲线方法，并且随着节点应力幅值增加，两种计算方法的寿命差距也在增大。这是由于在高应力水平情况下，应变控制的低周疲劳损伤在船体结构寿命衡量中不可忽略，且随着应力水平的增加，高低周复合疲劳模型中低周疲劳损伤的占比增加，S-N曲线方法预报的误差增大。另外，两种不同方法得到的疲劳寿命预报存在差异，船首处舱口角隅比船中舱口角隅的差异大，这是由于船首处舱口的应力水平整体高于船舯。因此，船首处舱口角隅处应变控制的低周疲劳寿命小于船舯，采用S-N曲线方法预报的疲劳寿命具有较好的准确性。