锚杆格构梁与抗滑桩联合支护下边坡的稳定性分析

卢晓强

(广西路桥工程集团有限公司,广西 南宁 530200)

0 引言

随着我国经济的快速发展以及“交通强国”战略的不断推进,我国加快了西部地区的交通基础设施建设,高速公路建设规模越来越大,覆盖范围越来越广。由于我国地域辽阔、地形复杂、山地所占面积在国土总面积中的占比>67%,因此在高速公路的设计与施工过程中,对高速公路沿线边坡进行稳定性分析和支护结构设计至关重要。目前已有很多学者针对边坡稳定性以及边坡支护方法进行了研究,并取得了大量的研究成果。常用的边坡稳定性方法主要包括极限平衡方法[1]和数值分析法[2]。其中,数值分析方法主要包括局部破坏判别法、有限元应力法以及强度折减法。陈祖煜、郑颖人、连镇营等[3-6]利用有限强度折减法对开挖边坡稳定性进行了较为全面的研究。叶帅华等[7]针对西部地区常见的二元结构深挖路堑边坡的稳定性进行研究,以某公路边坡实际工程为例,利用有限元方法研究了不同岩土体力学参数下边坡的稳定性以及变形破坏特征。刘杨等[8]基于饱和-非饱和渗流理论,建立有限元数值模型,对不同降雨条件下边坡的渗流过程进行了模拟,并利用强度折减法对降雨作用下的边坡进行了稳定性评价。边坡支护形式主要包括起支挡作用的各类挡土墙、抗滑桩和起锚固作用的系统锚杆、预应力锚杆(索)等。在实际的支护结构设计中,通常采用支挡与锚固共同作用的结构类型,如锚拉桩、预应力锚索框格梁等。史彧等[9]依托某高速公路改扩建工程中的岩质边坡支护工程,利用FLAC 3D软件建立数值模型,研究了预应力锚索的长度、倾角和预应力大小对边坡支护效果的影响。

本文以贺州至巴马公路金秀连接线的某高边坡支挡工程为例,利用Midas GTS软件进行数值计算,分析该边坡在锚杆格构梁与抗滑桩联合支护下边坡的稳定性,并针对锚杆格构梁进行参数敏感性分析,讨论不同的结构参数对边坡支护效果的影响,以期为其他高边坡支护结构设计提供参考。

1 数值模型的建立

1.1 Midas GTS简介

有限元方法是目前应用广泛的数值模拟方法之一,可将复杂几何体的计算难度大大降低。目前应用广泛的有限元软件主要分为两大类:通用有限元如ANSYS软件、ABAQUS软件等;应用于某些特定行业的专用有限元软件,如专用于岩土工程领域的Midas GTS软件等。本文将采取Midas GTS软件进行建模计算。

Midas GTS(Geotechnical and Tune Analysis System)软件作为岩土工程领域的大型有限元分析类软件,可以很好地应用于路基、边坡以及隧道等工程的数值仿真计算中。软件可以提供大量岩土材料常用的本构模型,还可以进行包括动力场、渗流场等的多场耦合计算,同时软件的交互性比其他软件更好,操作较为简便。

1.2 工程概况及支护设计方案

本文依托贺州至巴马公路金秀连接线的某高边坡支挡工程,该高边坡拟采用抗滑桩与锚杆格构梁联合支护。研究区内地形较为复杂,总体地势呈现中部高南北低的特点。边坡岩性组成自上而下分为粉质黏土、砂质黏性土、强风化砂岩、弱风化砂岩,其中粉质黏土因组成成分和含水率的不同,将其细分为粉质黏土a和粉质黏土b两层。坡面呈现上缓下陡的特点,根据坡度不同可分为4段,坡度分别为10°、20°、13°、55°,对应的坡体垂直高度分别为2.25 m、4.00 m、0.95 m、9.50 m。该边坡东部1.6 km处存在一条北东走向的活动断裂,倾角为35°～40°。在边坡附近无地表水的影响,同时地下水位埋藏较深,可忽略水对边坡稳定性的影响。

针对该边坡采取锚杆格构梁与抗滑桩联合支护方案,施工过程中边开挖边支护,支护后的边坡由上部的倾斜坡面、下部的垂直坡面以及两者间的平台部分构成,总坡高约为23 m,其中上部的倾斜坡面的坡率为1∶1,平台宽度为4 m。对上部倾斜坡面采取锚杆格构梁支护,格构梁的横梁间距和纵梁间距均为2 m,锚杆设置在格构梁的横梁与纵梁交叉的节点处,共设置了5排锚杆,其中第一排和第五排的锚杆长度为12 m,其余锚杆长度为15 m,角度取15°。对下部垂直坡面采取锚拉桩支护,桩间距为2.5 m,桩间设置挡土板,每根抗滑桩上设置4根预应力锚索,锚索之间的竖向距离为3 m。

1.3 数值模型的建立

利用Midas GTS软件对支护后的边坡建立计算模型并进行计算。在保证其符合工程实际情况的基础上尽可能简化其计算模型,建立计算模型如图1所示。

图1 计算模型图

如图1所示,x轴方向上的计算长度为30 m,y轴方向上的计算长度为65 m。z轴方向上,边坡背面一侧的高度为40 m;另一侧的高度为22.5 m。设置模型的边界条件为:模型底部约束其x、y、z3个方向的位移,模型四周约束其法向位移,模型其余的临空面设为自由边界。

边坡支护结构的本构关系选取为理想弹性模型,边坡岩土体的本构关系选取为摩尔-库仑模型。通过室内力学试验,得到该模型的力学计算参数如表1、表2所示。

表1 岩体力学参数取值表

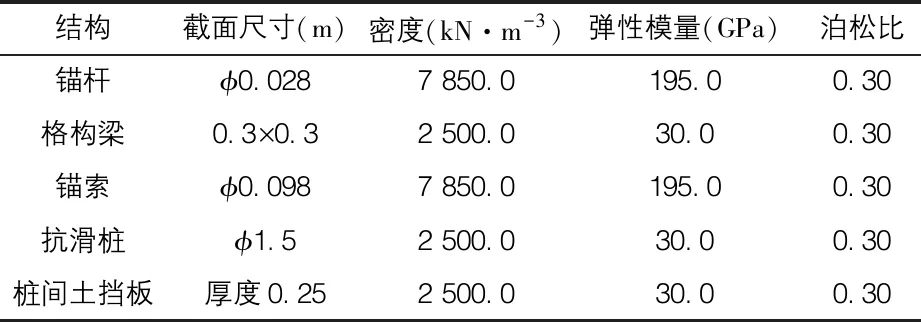
表2 边坡支护结构力学参数取值表

2 数值模拟结果分析

根据Midas GTS软件的计算结果,得到边坡以及支护结构的应力与位移分布。

2.1 边坡位移分析

根据数值计算结果,得到边坡表面位移分布如图2所示。

图2 边坡坡面水平位移曲线图

由图2可知,在边坡上部斜坡段,坡表位移随高程增大先增大后逐渐减小,最大位移出现在与平台竖向垂直距离约1 m的位置,位移值为25 mm。在边坡下部垂直坡段,从坡顶到第一根锚索位置的坡表位移随高程增大先增大后减小,在第一根锚索位置以下的坡体,其坡表位移出现多次反复剧烈的增大和减小。其原因是在预应力锚索以及该部分坡体中存在的多个不同岩土体分界面产生的共同影响。

2.2 支护结构应力分析

根据数值计算结果,本节重点对锚杆轴力以及抗滑桩的弯矩进行分析,得到锚杆轴力如下页图3所示。

图3 锚杆轴力变化曲线图

由图3可知,每排锚杆的轴力变化趋势基本一致,均表现为自锚杆末端到锚杆与格构梁的连接处逐渐增大,在锚杆与格构梁的连接处达到最大轴力值。同时,坡体自上而下,锚杆的最大轴力表现为先增大后减小的趋势,即第一排锚杆的最大轴力最小,为10.68 kN,第四排锚杆的最大轴力最大,为35.45 kN。

图4所示为中间抗滑桩的弯矩沿桩身分布图,桩身正弯矩主要出现在抗滑桩的锚固段,其中最大正弯矩出现在桩底位置,弯矩值为919.32 kN·m,分析其原因为抗滑桩桩端嵌固在高强度的弱风化砂岩中。桩身负弯矩主要出现在抗滑桩上部,其中最大负弯矩出现在抗滑桩与第四排预应力锚索相交的位置,弯矩值为1 000.01 kN·m。抗滑桩的桩身弯矩在与每根预应力锚索相交的位置均发生突变。

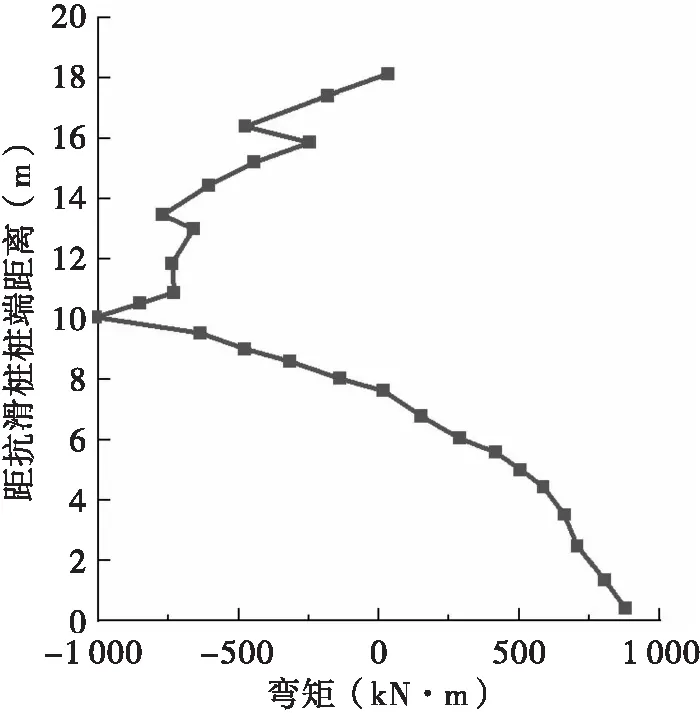
图4 中间抗滑桩弯矩变化曲线图

2.3 边坡稳定性分析

边坡的安全系数是通过强度折减法得到的。强度折减法是在重力加速度不变的情况下,按照式(1)、式(2)的方式对岩土体的强度指标c、φ进行折减与更新,逐步降低岩土体的强度指标,通过多次迭代计算,求得边坡岩土体临界破坏状态下的抗剪强度指标,此时得到的抗剪强度指标与岩土体实际的抗剪强度指标之间的比值,即为边坡的安全系数Fs[10]。

(1)

(2)

通过强度折减法计算边坡的安全系数,得到原始边坡的安全系数为1.54,仅完成格构梁与锚杆支护的边坡安全系数为1.88,完成全部支护后的边坡的安全系数为1.92,说明锚杆格构梁与抗滑桩联合支护方案对该边坡的加固效果很明显,在加固完成后边坡的安全系数较原始边坡提高了24.6%。

3 边坡支护效果的影响因素研究

由前文可知,边坡上部斜坡段的位移值明显大于边坡下部垂直坡段,说明边坡上部的稳定性较差,因此本节重点针对边坡上部的锚杆格构梁支护结构,采取控制变量法,分析不同的格构梁截面尺寸、锚杆长度、锚杆安设角度对边坡稳定性的影响。

3.1 格构梁截面尺寸对边坡稳定性的影响

为研究格构梁截面尺寸对边坡稳定性的影响,分别将格构梁的正方形截面边长取为0.1 m、0.2 m、0.3 m、0.4 m、0.5 m、0.6 m,建立数值模型进行计算,并求解不同工况下边坡的安全系数。不同格构梁截面尺寸下的坡面位移和抗滑桩弯矩如图5所示。

图5 不同格构梁截面尺寸下的坡面位移和抗滑桩弯矩变化曲线图

如图5所示,在任意格构梁截面尺寸下,边坡下部垂直段的水平位移最大值均大于边坡上部斜坡段。随着格构梁截面尺寸逐渐增大,抗滑桩最大弯矩表现出明显的线性增大趋势,边坡上部斜坡段的水平位移最大值逐渐增大,但增速较慢,边坡下部垂直段的水平位移最大值基本不变,表明格构梁截面尺寸对抗滑桩最大弯矩的影响较大,对坡面位移的影响较小。

对不同工况下的边坡求解安全系数,得到格构梁截面边长为0.1 m、0.2 m、0.3 m、0.4 m、0.5 m、0.6 m时对应的边坡安全系数分别为1.65、1.80、1.92、1.93、1.91、1.88,即随着格构梁截面的增大,边坡稳定性先升高再降低,当格构梁截面边长为0.40 m时,边坡安全系数最大,边坡的稳定性最高。

3.2 锚杆长度对边坡稳定性的影响

为研究锚杆长度对边坡稳定性的影响,分别将锚杆长度取为6.0 m、9.0 m、12.0 m、15.0 m、18.0 m,建立数值模型进行计算,并求解不同工况下边坡的安全系数。不同锚杆长度下的坡面位移和抗滑桩弯矩如图6所示。

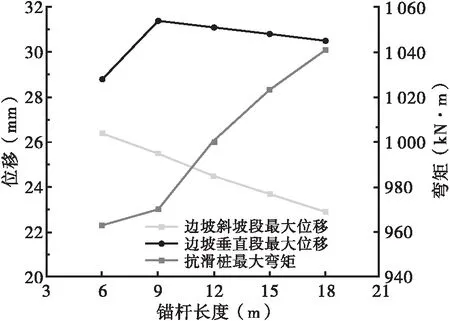
图6 不同锚杆长度下的坡面位移和抗滑桩弯矩变化曲线图

如图6所示,抗滑桩最大弯矩随着锚杆长度逐渐增大而增大,且当锚杆长度>9 m时,抗滑桩最大弯矩的增速明显变大。随着锚杆长度逐渐增大,边坡上部斜坡段的水平位移最大值呈现线性减小的趋势,边坡下部垂直段的水平位移最大值先增大再缓慢减小。

对不同工况下的边坡求解安全系数,得到锚杆长度为6.0 m、9.0 m、12.0 m、15.0 m、18.0 m时对应的边坡安全系数分别为1.11、1.27、1.92、1.91、1.92,即随着锚杆长度的增大,边坡稳定性先升高后保持稳定。结合图6所示,当锚杆长度<12 m时,坡面位移较大,抗滑桩弯矩较小,边坡安全系数较低,故锚杆长度应≥12 m,同时为节约材料成本,锚杆长度应取为12 m。

3.3 锚杆安设角度对边坡稳定性的影响

为研究锚杆安设角度对边坡稳定性的影响,分别将锚杆安设角度取为5°、10°、15°、20°、25°、30°,建立数值模型进行计算,并求解不同工况下边坡的安全系数。不同锚杆安设角度下的坡面位移和抗滑桩弯矩如图7所示。

图7 不同锚杆安设角度下的坡面位移和抗滑桩弯矩变化曲线图

如图7所示,随着锚杆安设角度逐渐增大,抗滑桩最大弯矩先增大再减小,边坡上部斜坡段的水平位移最大值和下部垂直段的水平位移最大值均基本不变,表明锚杆安设角度对抗滑桩最大弯矩的影响较大,对坡面位移的影响较小。

对不同工况下的边坡求解安全系数,得到锚杆安设角度为5°、10°、15°、20°、25°、30°时对应的边坡安全系数分别为1.91、1.98、1.92、1.86、1.70、1.22,即随着锚杆安设角度的增大,边坡稳定性先升高再降低,当锚杆安设角度为10°时边坡的安全系数最大、稳定性最高,当锚杆安设角度>25°时边坡的安全系数迅速减小、稳定性迅速降低。

4 结语

本文以贺州至巴马公路金秀连接线的某高边坡支挡工程为例,利用Midas GTS软件进行数值计算,分析该边坡在锚杆格构梁与抗滑桩联合支护下边坡的稳定性,并针对锚杆格构梁进行参数敏感性分析,讨论不同的结构参数对边坡支护效果的影响。本文得到的主要结论如下:

(1)利用强度折减法计算边坡的安全系数,得到原始边坡的安全系数为1.54,仅完成格构梁与锚杆支护的边坡的安全系数为1.88,完成全部支护后的边坡安全系数为1.92,在加固完成后边坡的安全系数较原始边坡提高了24.6%,说明锚杆格构梁与抗滑桩联合支护方案对该边坡的加固效果很明显。

(2)边坡下部垂直段的水平位移最大值均大于边坡上部斜坡段。格构梁截面尺寸对抗滑桩最大弯矩的影响较大,对坡面位移的影响较小,当格构梁截面边长为0.40 m时,边坡安全系数最大,边坡的稳定性最高。

(3)随着锚杆长度逐渐增大,抗滑桩最大弯矩逐渐增大,边坡上部斜坡段的水平位移最大值呈现线性减小的趋势,边坡下部垂直段的水平位移最大值先增大再缓慢减小。当锚杆长度<12 m时,坡面位移较大,抗滑桩弯矩较小,边坡安全系数较低,故锚杆长度应≥12 m。

(4)锚杆安设角度对抗滑桩最大弯矩的影响较大,对坡面位移的影响较小。随着锚杆安设角度的增大,边坡稳定性先升高再降低,当锚杆安设角度为10°时边坡的安全系数最大、稳定性最高,当锚杆安设角度>25°时边坡的安全系数迅速减小、稳定性迅速降低。