基于动载试验的既有板桥动力性能分析★
2023-09-22刘莉萍
杜 婷,刘莉萍,杨 阳
(1.陇东学院土木工程学院,甘肃 庆阳 745000; 2.甘肃省高校黄土工程性质及工程应用省级重点实验室,甘肃 庆阳 745000)
0 引言
我国早期建造的中小桥梁,随着运营年限增加,大部分出现损伤和病害等问题,为了避免安全事故的发生,如何评估通行期间的承载特性和运营情况可以通过定期的相关检测来获取[1-3]。根据《公路桥梁荷载试验规程》[4],通过桥梁荷载试验可以有效评定已建桥梁的实际承载特性,为该桥继续通行和维修养护提供理论支撑[5-8]。目前可以通过裂缝分析[9-13]、健康监测[14]和有限元分析[15-16]等方法对混凝土板桥的承载特性进行检测评估,而桥梁刚度、整体性和车辆运营安全性等特性还需根据其动力特性进行评判[17-18]。
本文以我国G309国道K1264+300处的混凝土板桥马莲河桥为研究对象,马莲河桥的桥墩和梁体均出现不同程度的开裂,部分支座出现倾斜和锈蚀,已影响车辆正常运行。通过对该桥采用有限元仿真模拟与桥梁动载试验,评估其自振频率、振型、阻尼比等动力性能指标,为既有板桥正常工作性能的检测和评定方法积累技术资料。
1 板桥概况
马莲河板桥于1975年10月8日建成,该桥桥跨结构采用7孔跨径为22.2 m的钢筋混凝土T型简支梁,由5片T梁组成,T梁净高135 cm,翼板高8 cm~14 cm,宽160 cm,桥梁全长170.5 m,桥面总宽8.5 m,净宽7.0 m,两侧各设置0.75 m的人行道,两车道双向行车,桥上净高4.5 m,桥下净高22.7 m,桥墩为重力式桥墩,桥台为U型桥台,基础为扩大基础,支座为球形支座。主梁采用C25混凝土,桥面铺装、墩帽和台柱都采用C20混凝土,设计荷载为汽—13级,拖—60。
为方便试验时进行数据记录,统计该桥主要承重构件数量并进行编号,具体参见表1。

表1 桥梁构件编号表
2 动载试验
2.1 试验原理
为了获取该既有板桥结构的固有振动特性,检测时采用脉动法研究马莲河板桥的动力特性,即采用数学方法对现场试验所记录的各测点振动的响应信号进行分析。由于脉动法监测的振动响应信号是桥梁只受大地和外界环境激励时产生的,振幅较小,因此需在桥面上布置高灵敏度的低频横向、竖向和纵向拾振器记录桥梁振动情况,根据桥梁结构形式,动载测试点主要布置在各跨跨中截面和2号墩顶截面处,该点包含了较多的环境激励成分,具体布置如图1所示。

由于采样时间越长,频域数据和振型精准程度越高,试验时采样时间设置为30 min,可使信号较平稳,提高精度。数据采集分析系统采用与传感器配套的放大器,将传感器采得的信号放大或转化为电压量,可提供各被测点的位移参量。
2.2 试验结果
记录脉动试验得到的第一跨至第七跨竖向、第二跨横向及纵向脉动时程曲线,通过傅里叶变换得到频域信号,利用谱分析可以得到各桥跨的固有自振频率和频率分布特征等动力参数。进行数据分析时,选用时间窗函数进行谱分析,并设置为低通滤波器以确保数据的可靠性,同时选用较多的平均次数和重叠率以提高信号谱分析的精确度,据此得到第二跨的功率谱密度函数分析曲线如图2所示。
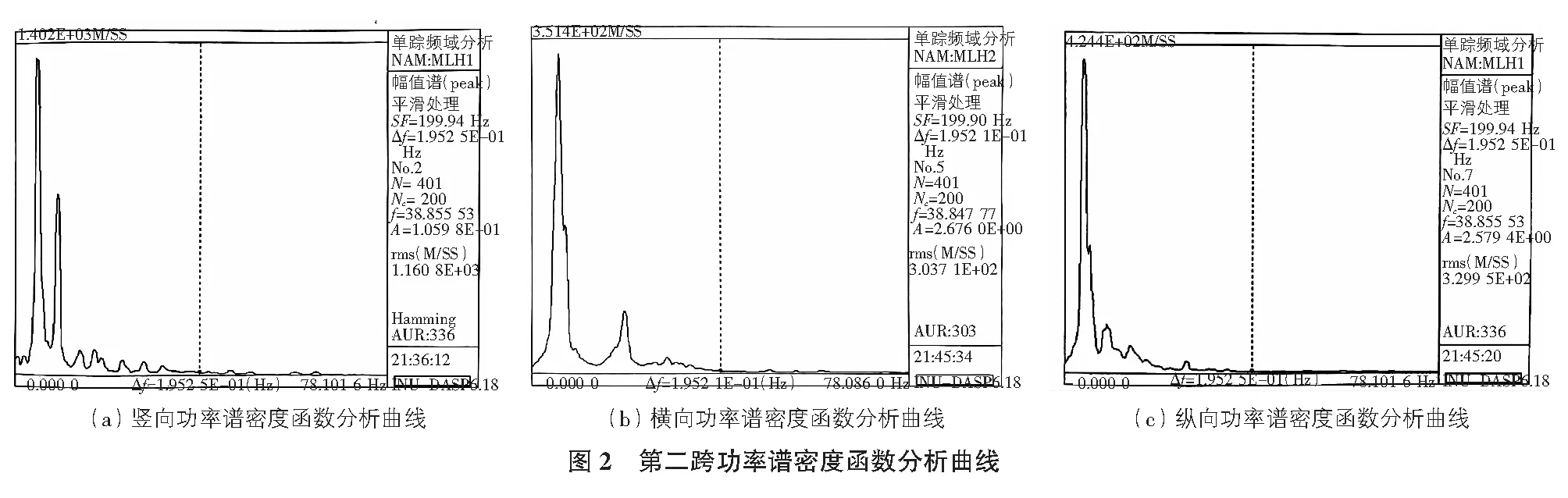
2.3 频域计算法
在计算桥梁自振频率和阻尼比的实测值时,由于采用大地脉动法得到的振动幅度值较小,使计算结果误差较大,因此采用频域计算方法进行计算。为了得到准确度高的阻尼结果,采用DASP软件中的INV频率计技术,可以避免频率分辨率不高使结果误差较大的问题。INV频率计技术需要采集大容量连续不间断的振动信号,然后对所选频域进行傅里叶变换计算,计算时每进行一次傅里叶变换都要使用所有数据以提高频率分辨率,进而获取比较高的精度。计算时在软件中选择“瞬时频谱计算”方法,采用软件计算模块中的“INV阻尼计法”,会在所选的“瞬时频谱图”上显示桥梁结构自振频率和阻尼比这两个参数的计算结果。
3 数值模拟
3.1 模型建立
根据马莲河板桥的实际构造情况,采用有限元分析软件Midas/civil建立该桥的数值计算模型,通过模态分析得到该桥的自振频率和振型等动力参数,并据此检定和评估板桥马莲河桥的承载能力、车辆通行能力和整体工作性能等。具体步骤如下:
1)结构离散化。根据马莲河板桥的结构特点,混凝土T梁、横隔板和桥墩均采用梁单元进行模拟;5片T梁采用刚臂连接;同时对划分的单元和节点进行编号。
2)结构描述。选取整体坐标轴,并输入结构特征,该板桥各构件的性能参数如表2所示,基础采用固定约束的形式进行模拟。
3)桥上施加的荷载根据脉动试验的特点,采用等效荷载的形式将桥面铺装、栏杆和人行道等加载到梁上。
4)对结构的动力平衡方程组进行求解得到结构的自振频率和振型等参数。
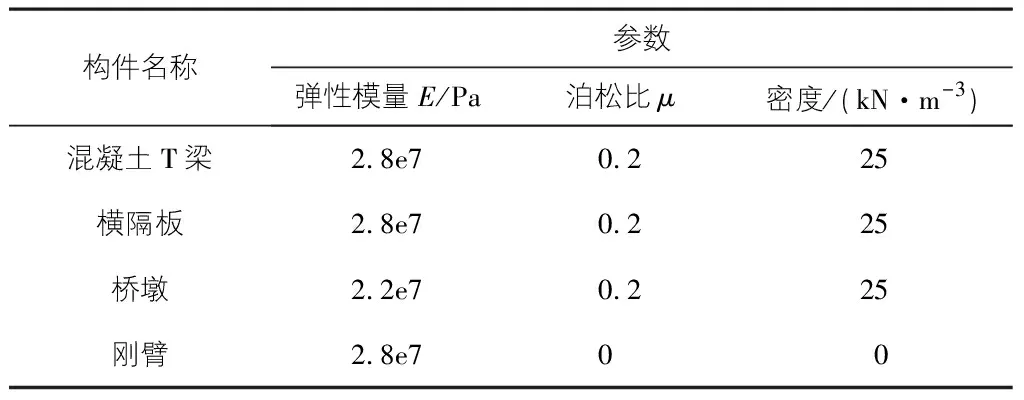
表2 构件性能参数表
根据上述步骤建立桥梁第二跨的空间有限元计算模型,如图3所示。

3.2 自振频率
在考虑混凝土T梁自身重量、横隔板质量的情况下通过子空间迭代法对建立的该板桥第二跨空间模型进行模态分析,理论计算得到各阶振型如图4所示。子空间迭代法在计算时不仅利用rayleigh-ritz法将刚度矩阵和质量矩阵在子空间投影,缩减自由度,而且同时以逆代的形式进行迭代,在反复迭代中使振型逐步趋近精确值,得到桥梁结构自振频率的理论值。通过汇总得到马莲河板桥纵向、横向和竖向所对应自振频率的理论值和实测值如表3所示。
由表3可知,马莲河板桥纵向和横向自振频率的实测值分别为3.90 Hz和5.47 Hz,大于计算值2.09 Hz和4.83 Hz,说明桥梁结构纵向和横向动力刚度满足要求,而竖向自振频率的实测值为4.68 Hz,比计算值5.98 Hz小,说明其竖向刚度不满足要求,需要采取措施进行加固。同时,纵向自振频率小于横向自振频率,说明支座对该桥纵向和横向的约束效应不同,振动时支座的纵向约束大使桥梁纵向按低频振型振动,而横向约束较小使桥梁横向按较高频率振型振动。


表3 马莲河板桥自振频率的理论值和实测值 Hz
3.3 阻尼比
根据INV频率计技术计算得到马莲河板桥阻尼比的实测值如表4所示。

表4 马莲河板桥阻尼比实测值 %
由表4可知,马莲河板桥的横向和纵向实测阻尼比分别为0.043和0.028 7,满足桥梁结构阻尼比在0.01~0.08之间的要求,说明桥梁结构具有一定耗散外部能量的能力,振动衰减较快,满足继续通行条件。而横向振动的阻尼比大于竖向振动的阻尼比,主要是由于横向振动时5片T梁连接的每个支座都相当于一个耗能元件,提高了系统的阻尼比。
4 结论
通过对马莲河混凝土板桥进行动载实验和数值模拟,得到该桥竖向自振频率的实测值为4.68 Hz小于计算值5.98 Hz,说明该桥的竖向刚度不足,已不满足设计要求。而该板桥纵向和横向自振频率的实测值为3.90 Hz和5.47 Hz,分别大于计算值2.09 Hz和4.83 Hz,说明其纵向和横向的动力刚度满足要求。同时利用INV频率计技术计算得到该桥横向振动和竖向振动时的阻尼比分别为0.043和0.028 7,说明该桥结构具有一定耗散外部能量的能力,振动衰减较快,满足继续通行条件。根据所得结论,为保证该桥运营安全,对其进行维修加固建议如下:
1)由于该桥竖向刚度不足,需对该桥梁体进行加固,增强梁体承载力以满足通行要求。2)对梁体和墩身的裂缝进行修补,对1号、2号桥墩进行加固。3)加强该桥的维护和管理,实行限载通行,以满足维持交通通行的要求。

