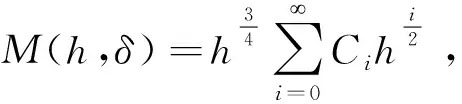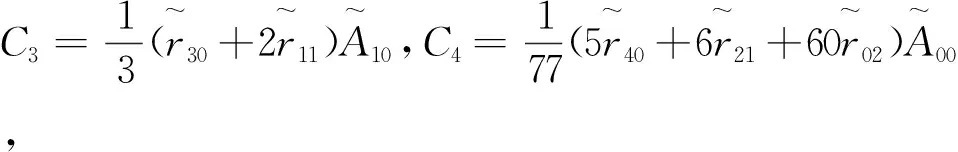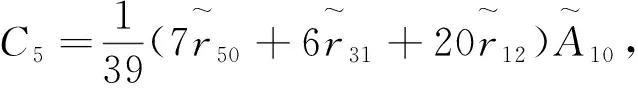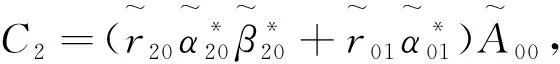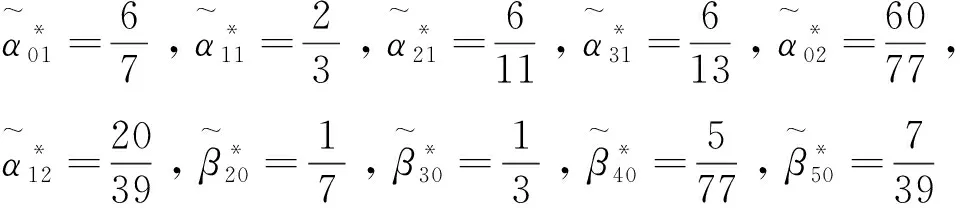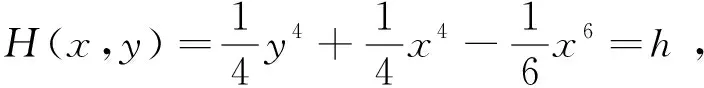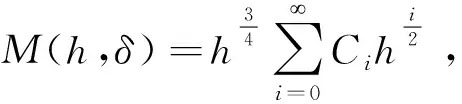一类退化中心附近的Melnikov展开式

尚德生

(山东理工大学 数学与统计学院，山东 淄博 255049)

平面动力系统分支理论研究中的一个重要的课题就是中心型奇点附近的极限环分支研究。当一个平面系统的奇闭轨是同宿或异宿于双曲鞍点时,已经有比较完善的理论和应用成果[1-3]。当奇闭轨是同宿或异宿于非双曲鞍点,或者更加复杂的退化奇点(如退化鞍点或尖点)时的分支研究,却非常复杂。对于奇点是幂零鞍点和幂零尖点的情形下的奇闭轨分支,已有比较系统的讨论[2,4-5],并陆续对不同类型的相关微分系统作了讨论和应用[6-8]。对更进一步的退化奇点情形的同宿或异宿分支问题,文献[9]对退化尖点环附近的Melnikov函数展开式作了一些探索。虽然中心奇点附近的极限环分支研究成果非常丰富,但是主要集中于初等中心附近的Hopf分支研究,对非初等中心附近的分支问题研究却比较困难,学者利用Melnikov函数法讨论了幂零中心附近的展开及应用[10-11],对于幂零奇点的分类也给出了相应的讨论[12]。

本文在文献[2,5,9-10]的启发下,对一类退化中心附近的Melnikov函数的展开式进行探讨,并对m=1,n=1或2的情况,给出比较直观的结果。

考虑微分系统

(1)

式中p(x,y),q(x,y) 为x,y的多项式。

假设在ε=0时,对应的Hamilton系统:

(2)

相应的Hamilton函数H(x,y)=h满足H(x,y)=H1(x)+H2(y),且H1(x),H2(y)满足:

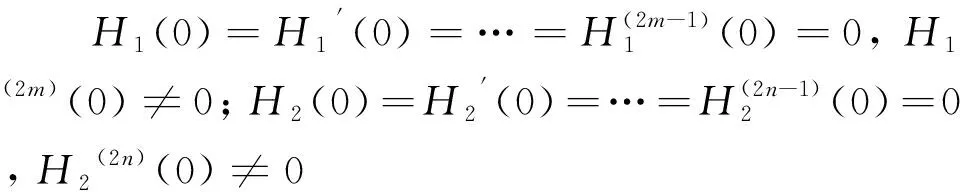
说明:i)当m=n=1时,原点是未扰系统(2)的初等中心;ii)当m,n中一个等于1,另一个大于1时,原点是系统(2)的幂零中心;iii)当m,n都大于1时,原点是系统(2)的退化中心。

不失一般性,假设H1(2m)(0)>0,H2(2n)(0)>0,而且未扰系统(2)存在围绕原点(0,0)的一簇周期闭轨Lh,h∈Jα=(0,α),其中α>0。由假设,不妨设H1(y),H2(x)满足:

其中

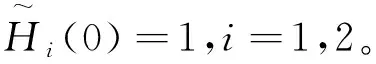
的零点个数来确定。

因此根据格林公式,只需要讨论系统(1)的一阶Melnikov函数:

(3)

式中:

其中δ∈Rn是系统(1)的扰动参数。

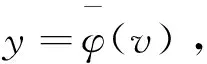
H1(x)=u2m,H2(y)=v2n,

(4)

且满足xu>0,yv>0成立。

若设

(5)

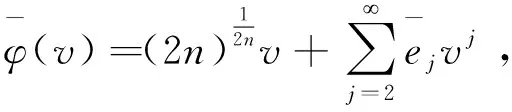
(6)

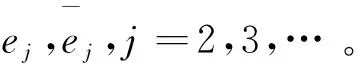
这样将式(5)、式(6)代入式(3)得

(7)

利用周期轨Lh关于坐标轴的对称性,并借助计算机软件计算得到

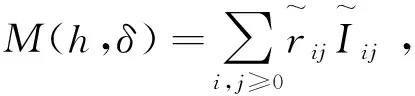
(8)

(9)

利用对称性容易得到

(10)

且有下述结论成立。

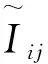
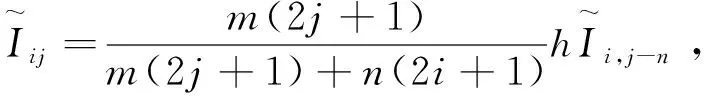
(11)

(12)

证明这里只需要计算

首先利用分部积分法,得

即得

整理可得式(11)成立。

同样利用分部积分法可得

即

整理可得式(12)成立。

因为对任意i,j存在唯一的非负整数l,k,r,s,使得i=ml+r,j=nk+s,其中0≤r≤m-1,0≤s≤n-1。根据引理1递推可以得到引理2。

引理2对非负整数i,j=0,1,2,…,有

(13)

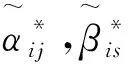
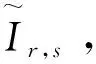
引理3当0≤r

(14)

因此,利用式(7)、式(8),结合引理1—引理3, 可得Melnikov函数在h=0 附近的展开式。

定理1在Hamilton函数满足前面所给退化中心的假设下, 系统(1)在退化中心附近的Melnikov函数展开式为

M(h,δ)=

(15)

说明: 定理1中, 当n=1时,则有s=0, 这时式(15)变为

这个结果与文献[10]的结果相同。

在m=2,n=1时, Melnikov函数展开式有推论1。

推论1在m=2,n=1时,系统(1)在幂零中心附近的Melnikov函数展开式为

(16)

式中展开式的系数:

推论1的证明,利用引理1—引理3和定理1, 利用

在m=2,n=2时, Melnikov函数展开式有推论2。

推论2在m=2,n=2时,系统(1)在退化中心附近的Melnikov函数展开式为

(17)

式中展开式的系数:

其中

推论2的证明,利用引理1—引理3和定理1, 得到:

而且

本文用一个例子加以说明。

例1对系统

(18)

式中q(x,y)=y(a0+a1x+a2x2+a3x3+a4x4)+

y3(a5+a6x+a7x2)+a8y5。

(19)

为使得变换

(20)

成立,可设x=φ(u),其中

(21)

代入式(20),借助计算机软件计算可递推得

当j为偶数时,ej=0,且

这样根据推论1直接计算可得

(22)

式中:

C0=7.416 299a0;

C1=2.221 441a0+4.442 883a2+

13.328 649a5;

C2=3.090 124a0+4.120 166a2+

4.944 199a4+3.388 852a5+

6.777 705a7+24.720 996a8;

C3=5.939 271a0+7.127 125a2+

7.775 045a4+4.165 203a5+

5.553 604a7+5.553 604a8;

C4=53.115 806a0+60.703 778a2+

64.274 589a4+7.248 379a5+

8.698 054a7+6.180 249a8;

C5=32.443 266a0+36.048 073a2+

37.615 380a4+14.915 668a5+

17.046 478a7+9.898 784a8。

直接计算可得雅可比行列式

因此得到系统(18)在原点附近至少有5个极限环存在。