天气衍生品气温预测模型探索研究

郑涛涛,韩笑笑,陶祥兴,季彦颋

(浙江科技学院 理学院,浙江 杭州 310023)

近年来,灾害天气的频发对城市及企业的发展产生了很多不利影响。我国每年因气象灾害损失惨重。2021年下半年,河南、山西等地日降雨量突破历史极值,多地遭遇超强暴雨,给城市发展和人民生活带来了极大危害。郑州商品交易所与中国气象局签署战略合作框架协议,双方合作编制气温指数、研发天气衍生品。2020年11月27日《应对气候变化报告2020:提升气候行动力》显示:全球变暖的趋势仍然存在,全球气候变化可能会严重威胁自然生态系统、经济社会的发展和人类健康,要正确认识和防范气候风险。同时,非灾难性天气变化对生产经营造成影响也不容忽视,如能源公司因天气变化而引起的需求变动导致销量下降等,而天气衍生品的推出能够很好地帮助这类公司规避风险,稳定收入。

在针对天气衍生品的研究中,定价问题备受关注。市场上大多数投资者使用历史燃烧分析(Historical burn analysis,HBA)的定价方法[1]。然而,Jewson等[2]研究已表明:HBA方法虽然简单易操作,但也易造成极大的定价错误。如今,更多的是利用动力学模型直接模拟未来温度的变化。每日气温建模方法较全面地利用了日均气温(Daily average temperature,DAT)的历史数据,相较于HBA、精算定价法或指数建模法等其他方法,其定价更为准确[2]。目前的研究中,主要有两种方法来对DAT建模,一种是离散过程的建模,如时间序列模型AR[3]、ARMA[4]、ARIMA[5]、SARIMA[6]、AR-GARCH[7]以及基于温度的傅里叶变换[8-9]等;另一种则是连续型随机过程建模,根据DAT历史数据表现出的均值回复特征,通常采用奥恩斯坦-乌伦贝克(Ornstein-uhlenbeck,OU)过程建模[5,9-12]。以OU过程为基础,采用一个正弦函数描述气温显著的季节性变化[10]。同时,在气温波动中,季节性变化也较为明显,根据气温波动的特点,将气温波动视为一个分段连续函数,每月波动为一常数[10]。Mraoua等[13]将气温波动同样也用一个OU过程进行刻画。然而,分段恒定的波动会低估实际的波动,导致天气衍生品价格被低估,且模型的正态性检验假设通常不成立[8]。此外,气温波动表现出显著的自相关特性,分数布朗运动(Fractional brownian motion,FBM)能够刻画具有长期依赖性的随机过程[14]。由于日均气温温差近似服从正态分布,故对于噪声部分通常采用布朗运动[3,10,13]或Lévy过程[15]进行刻画。除此之外,CAR过程[6,16]、人工神经网络[17]和小波神经网络(Wavelet neural network,WNN)[18]等方法也被用于DAT的建模。天气衍生品的定价精度取决于气温预测模型的精度,笔者采用连续型随机过程建模方法,在已有文献基础上,对气温波动的动力学模型部分深入研究,在气温波动项中增加时变的均值回复速度,使模型满足正态分布的原假设。另外,采用已提出的基于时间序列与随机过程方法构建的3个模型,评估笔者修正后模型的有效性,分析预测模型的精度对期权定价准确性的影响。

1 天气衍生品概述

天气衍生品(Weather derivatives,WD)是组织或个人为了降低不利或意外天气条件相关风险而衍生出来的金融产品,对于对冲因天气变化导致商品需求变化而产生的成交量风险来说是一种有效的工具[19]。天气衍生品对气象进行量化,将温度、降雨和风等气象指数作为标的物,收益取决于这些气象指数,主要面向于非灾难性的天气事件,其标的资产没有价值,不能被存储或交易。

目前,气温指数相关的衍生品在国外市场上最为常见,CME主要以气温期货与期权交易为主,交易期限通常为月度或季度。温度指数主要有积温指数(Cumulative average temperature,CAT)、制热指数(Heating degree day,HDD)以及制冷指数(Cooling degree day,CDD)。CAT主要适用于温度季节性变化不明显的地区,根据中国的气温变化特点,采用HDD与CDD对衍生产品进行定价。HDD定义为日均气温低于基准温度的度数,此时认为人们会产生取暖需求。芝加哥商品交易所(Chicago mercantile exchange,CME)目前将基准温度定为65 ℉(18.33 ℃),笔者研究中杭州市DAT数据的均值为18.3 ℃,故考虑取基准温度为18 ℃。HDD在一段时间的累加值,记为HDDs。CDD定义为日均气温高于基准温度的度数,此时认为人们会产生制冷需求。CDD在一段时间的累加值,记为CDDs。计算式分别为

(1)

(2)

式中:Hi为HDD;H为HDDs;Ci为CDD;C为CDDs;Tδ为基准温度;Ti为第i天的日均温度。

2 模型建立

日均气温的变化表现为自然气候规律的季节性变化以及近年来由于全球变暖而出现缓慢增长的趋势,同时由于其他气象因子的综合影响,气温变化表现出随机性,且个别气温出现极高或极低的现象。以气温指数作为标的物的天气衍生品主要关注的是非极端天气的变化,故在描述气温变化时,参数方法可作为有效的建模工具。

2.1 模型构建

由于差分后的DAT近似服从正态分布,且DAT表现出明显的均值回复的特征,故采用OU过程进行建模,模型为

(3)

St=a1+b1t+αsin(ωt+φ)

(4)

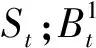
气温方差时序图如图1所示。由图1可知:气温波动长期回复到一均值,且无明显的趋势,经ADF检验可知序列平稳。气温方差ACF图如图2所示。

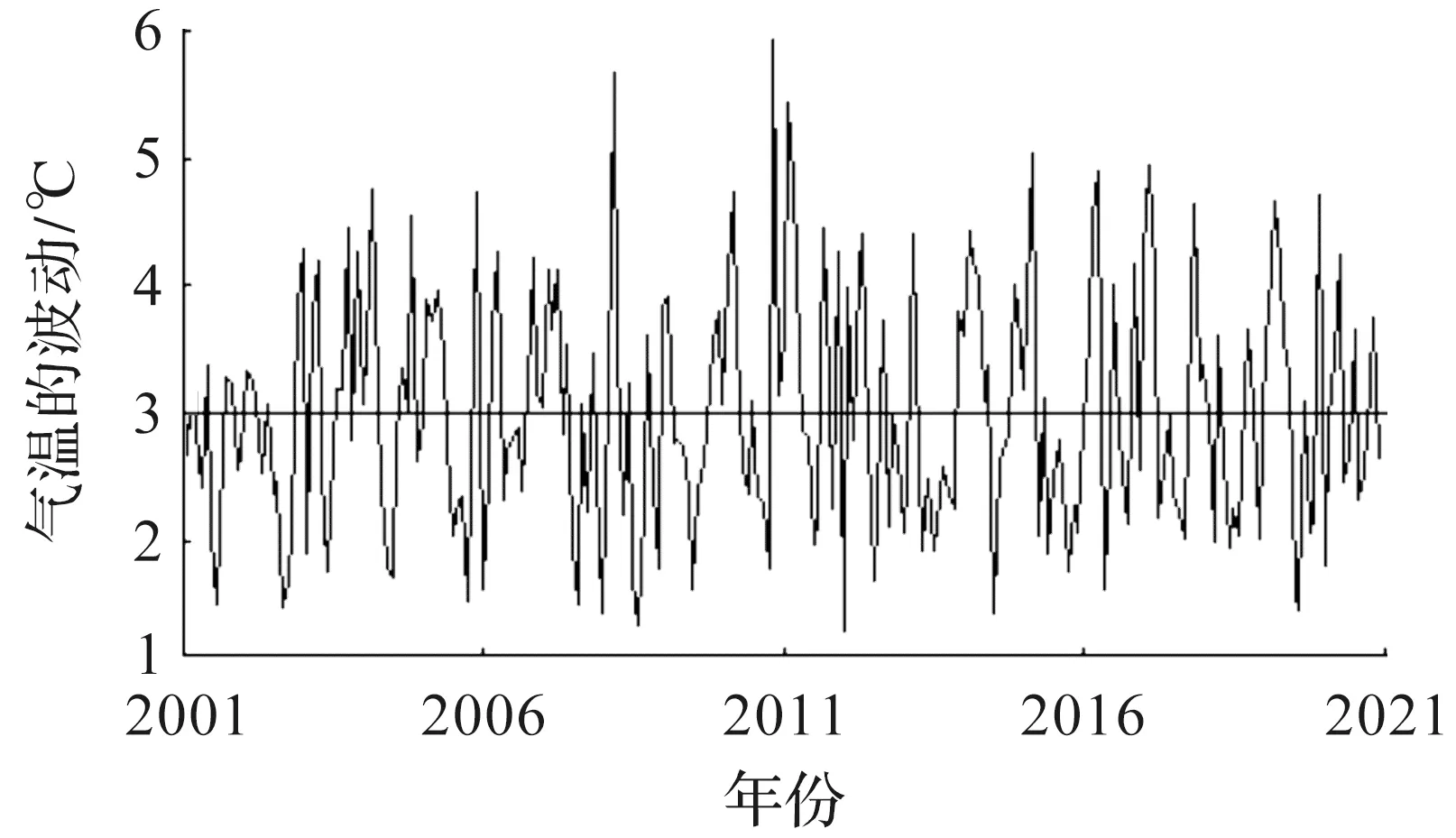
图1 气温方差的时序图

图2 气温方差的ACF图

由图2可知波动率中存在季节性和周期性。故σt同样采用OU过程表示为

(5)

Yt=a2+βsin(ωt+φ)

(6)

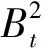
(7)

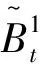
2.2 参数估计方法

对于St与Yt,首先将式(4,6)简化,然后采用最小二乘法估计其参数,计算式分别为

St=a1+b1t+c1sinωt+d1cosωt

(8)

Yt=a2+c2sinωt+d2cosωt

(9)

式中:c1=αcosφ;d1=αsinφ;c2=βcosφ;d2=βsinφ。

气温的月波动虽然同比差异不大,但是环比差异较大,故认为σt为一分段连续函数[10]。气温月波动率的计算式为

(10)

(11)

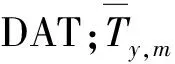
(12)

(13)

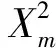
(14)

3 模型仿真

对St与Yt进行拟合,拟合结果分别如表1,2所示。

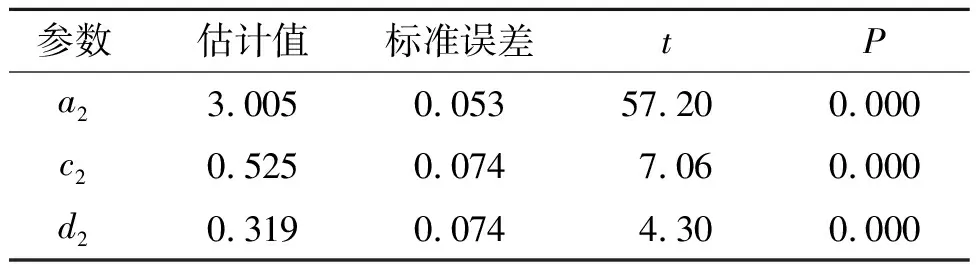
表2 Yt参数估计结果

考察Yt的残差,由Yt残差的ACF图3可知:季节性基本消除,且序列不存在自相关。将式(5)离散化为

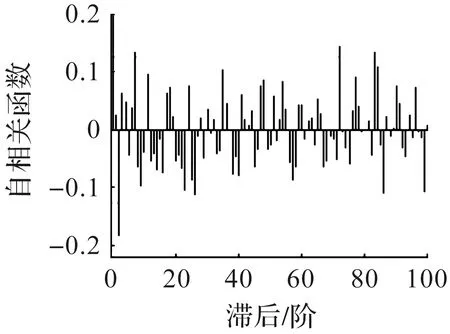
图3 Yt残差的ACF图

(15)

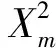
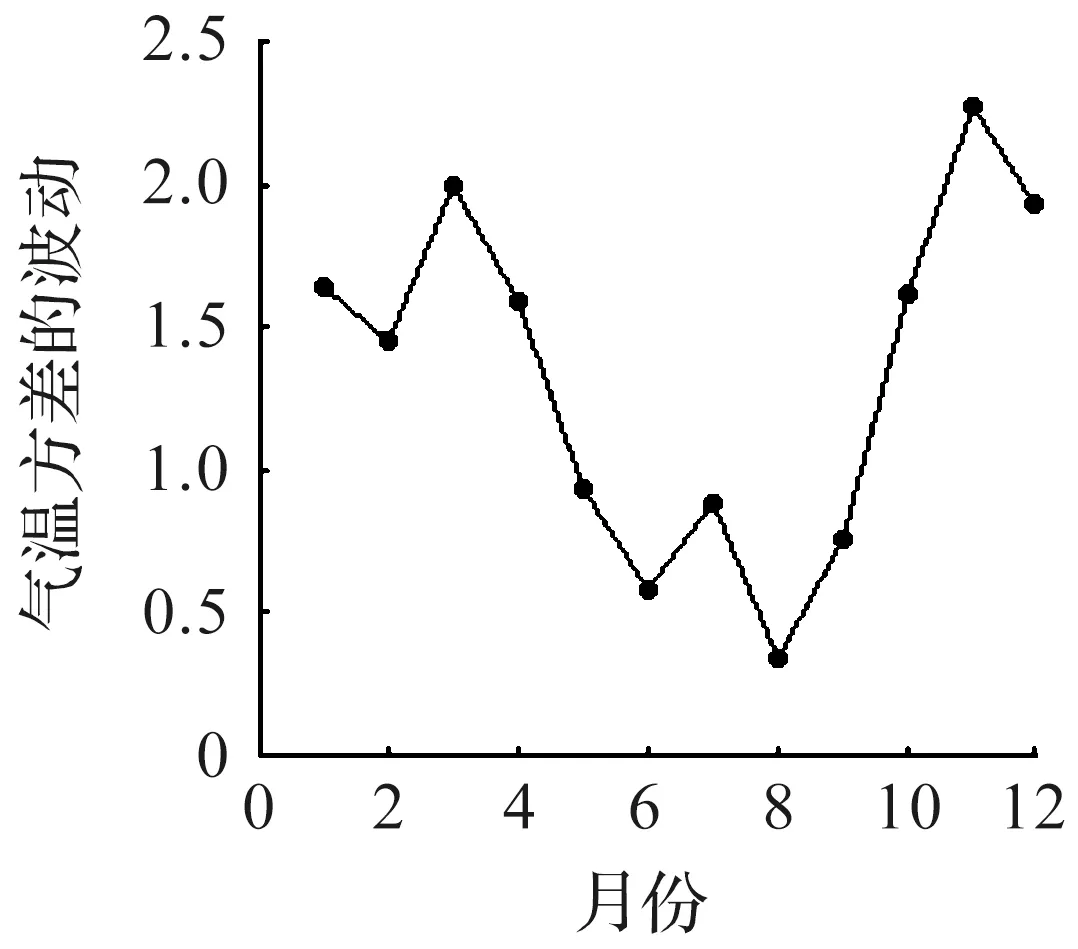
图4 气温波动的月波动

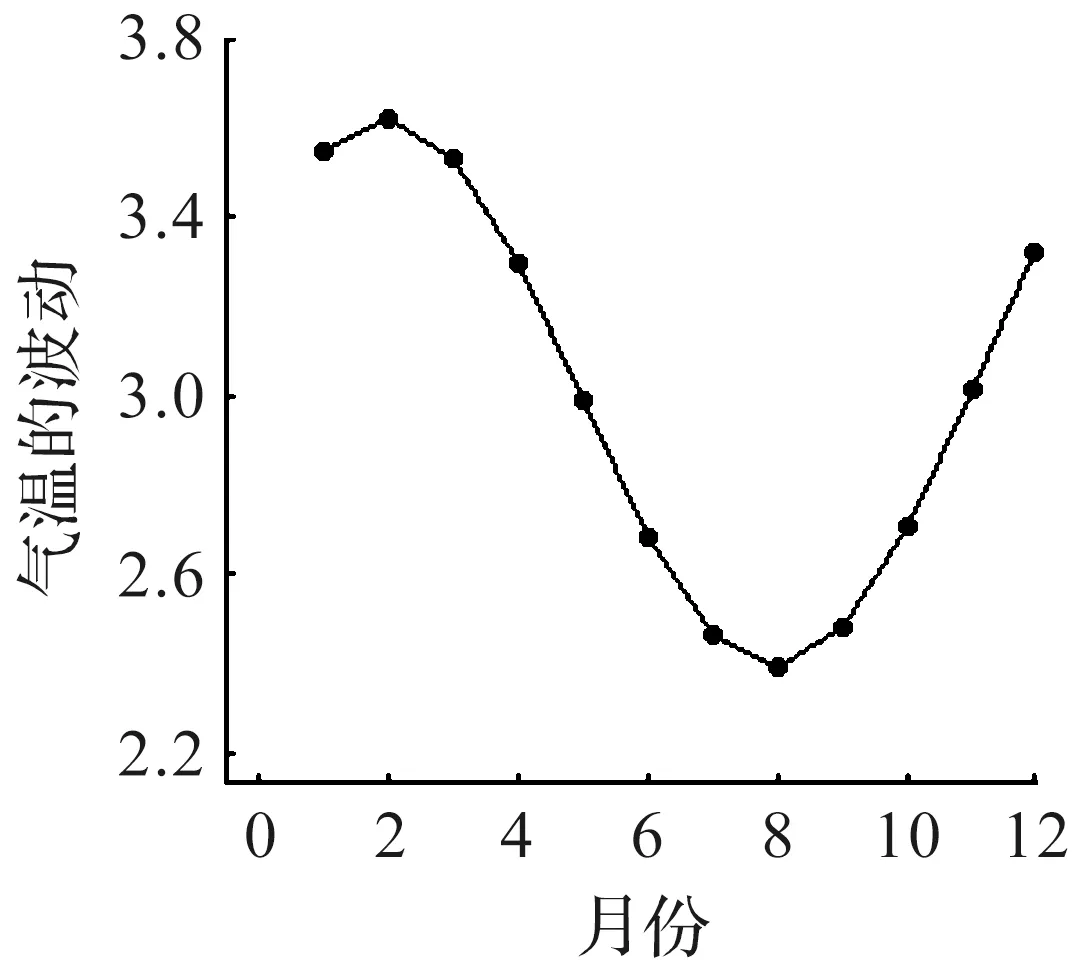
图5 气温的月波动

考察σt的残差,由ACF图6可知式(6)基本消除气温波动序列的季节性。σt残差的QQ图和直方图分别如图7,8所示。由图7,8可知:经过Kolmogorov-Smirnov检验,P显著大于0.05,残差序列服从正态分布。

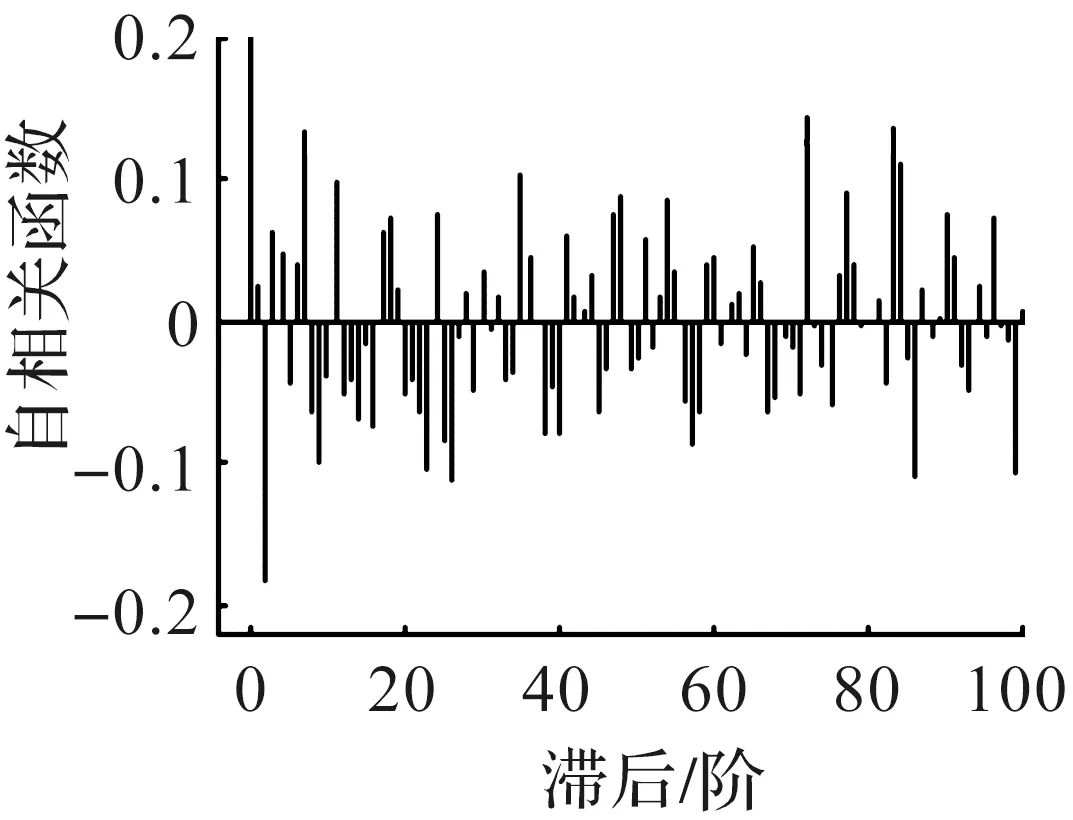
图6 σt残差的ACF图

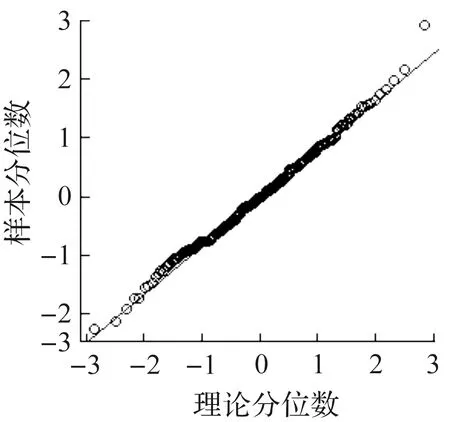
图7 σt残差的QQ图

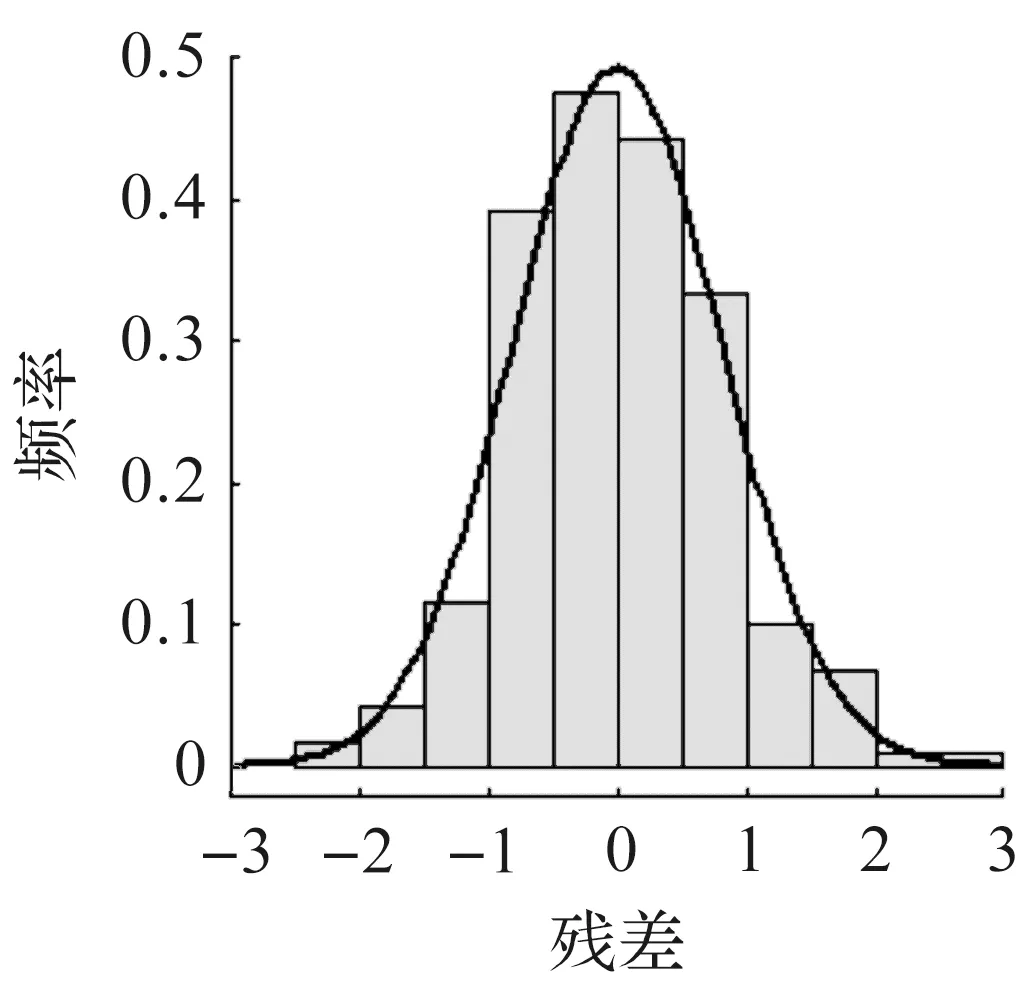
图8 σt残差的直方图

由上述结果估计κt及λt,参数估计结果如表3所示。

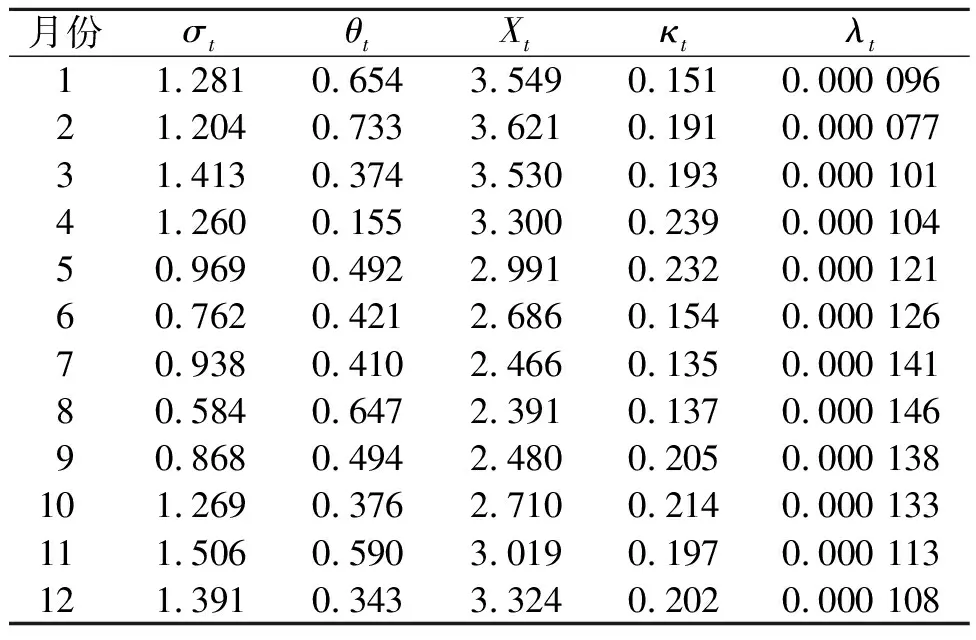
表3 参数估计结果

由表3估计结果可知:κt夏季较低,冬季较高,λt则相反,表明气温波动较大时,气温被拉回的速度更快,且在等价鞅测度下,风险的市场价格更高。结合以往相关文献可以得出:数据中的有效信息提取得越充分,估计的风险市场价格就越低。

4 模型评估

基于上述模型,对杭州市2021年的DAT进行预测,预测结果如图9所示。由图9可知时变OU模型可以很好地模拟杭州市DAT的基本走向。

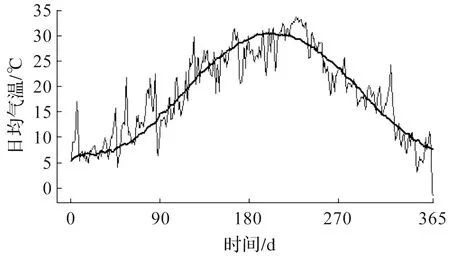
图9 气温预测结果

为了评估笔者模型的有效性,采用Svec等[8]提出的时间序列模型与Benth等[3]提出的随机过程模型作对比。其中,时间序列模型中DAT的长期趋势、季节性变化和气温波动项分别由一次线性函数、低阶傅里叶级数以及ARCH模型刻画,该模型记为M1。然而在仿真气温变化的过程中发现:DAT的波动项中存在明显的季节性、自相关特征以及ARCH效应,单一的ARCH模型无法充分提取这些信息,故对其进行修正,加入低阶傅里叶级数描述波动项的季节性,采用ARMA-GARCH描述自相关特征并消除ARCH效应,修正后的模型记为M2。随机过程模型则是采用OU模型在刻画气温波动部分,均值回复速度为恒定不变的常数,该模型记为M3。在M3模型的基础上,修正气温波动的均值回复速度为随时间变动的函数,解决了模型残差项不能通过正态性检验的问题,模型记为M4。

基于上述4个模型,进一步结合蒙特卡洛(Monte carlo,MC)模拟方法,模拟气温指数,并通过相对误差评估4个模型的精度。经计算,杭州市2021年1月至2021年3月的HDDs以及2021年5月至2021年7月的CDDs的真实值分别为1 251.0和1 251.2,MC模拟对比结果如表4所示。

表4 气温指数MC模拟对比结果

由表4的模拟结果可以看出:M4在该数据集上的表现优于其他3个模型,且HDDs和CDDs具有相近相对误差,结果较为稳定,表明连续型模型更能反映气温的变化情况;即使优化后的M2精度有所提升,其在该数据集上的表现整体来说也并没有比连续型模型M3,M4更优秀,尤其在对HDDs拟合时偏差较大。

M1,M2残差的QQ图和直方图如图10,11所示。由图10,11可以看出:模型M2的残差项虽然得到了修正,但是并未满足正态性假设条件。

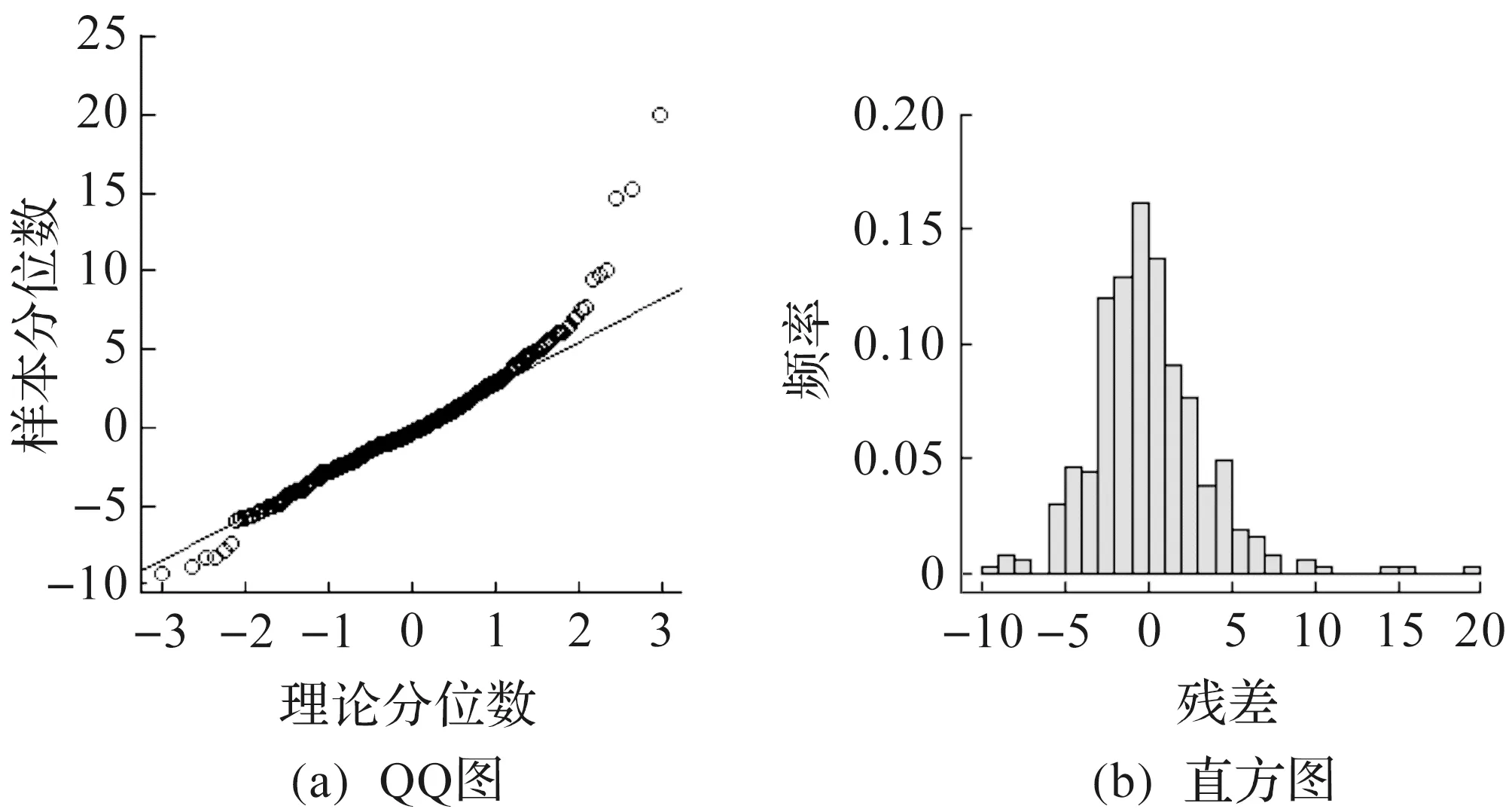
图10 M1残差的QQ图和直方图

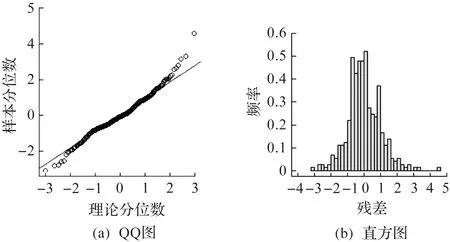
图11 M2残差的QQ图和直方图

5 期权定价

以气温期权季度交易为例,利用上述4个模型100 000次HDDs与CDDs的MC模拟结果,采用风险中性定价方法,对气温期权进行定价研究。以CDD欧式看涨期权为例,合约如表5所示。

表5 CDD欧式看涨期权合约

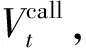
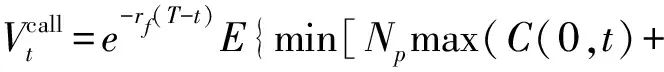
C(t+1,T)-K,0),U]}t∈[0,T]

(16)

式中:rf为无风险利率,rf取为2.576%(取自2021年5月的3月期SHIBOR利率);T为合约到期日;t为现在时刻;Np为单位气温指数名义价值,设为10 CNY;K为执行价;U为合约上限值,设为10 000 CNY;C(t1,t2)为从t1到t2时刻的CDDs;C(0,t)为实际值;C(t+1,T)为蒙特卡洛模拟的预测值。基于上述4个模型,根据式(16),2021年5月1日该合约的价格分别为1.65,5.50,9.61,16.89 CNY。然而事实上,当日真实合约价格为85.26 CNY,基于M4的期权定价偏差较M1,M2,M3分别下降了17.87%,13.36%,8.54%,因此,高精度的气温预测模型能够有效改善期权定价错误被放大的问题,减小因模型精度不高等问题带来的经济损失。

6 结 论

笔者首先在已有研究的基础上,对气温预测模型进行改进,将气温波动的均值回复速度修正为随时间变动的函数,通过对杭州市气温数据进行仿真,结果显示模型残差项满足正态分布的假设;然后通过与前人提出的模型以及修改后的模型作对比来评估笔者模型的有效性,蒙特卡洛模拟结果表明笔者模型精度高于其他3个模型;最后以笔者模型的预测结果为基础,对天气期权进行合理定价,结果显示笔者模型有效改善了期权定价错误被放大的问题。气象变化是多因素的,参数方法建模虽然能够捕捉到有规律的气温变化,但是对于夏季气温过低或冬季气温过高等异常天气的不规则变化,预测则会出现偏差。另外,当前的模型不够精简,这为模型的应用及推广造成了一定困难,后续将寻找既简单又行之有效的建模方法,如非参数方法,这将作为下一步研究的主要方向。目前,针对国内现存的天气衍生品发展问题,提出以下建议:1) 提高气象测量水平,降低数据壁垒;2) 因地制宜,加快主要城市气温指数的编制;3) 加强专业人才的培养,拓展天气衍生品种类。

本文得到了浙江科技学院研究生教学改革项目(2021yjsjg09)的资助。