考虑直流偏置抑制的单相逆变器改进控制方法

周超

（铜陵学院电气工程学院，安徽 铜陵 244000）

0 引言

逆变器可将交流电能转换为直流电能，被广泛应用于不间断电源（uninterruptible power supply，UPS）、交流调速、新能源发电、储能等众多领域［1-5］，输出电压质量和动静态性能是衡量逆变器性能的关键指标［6］。

单相逆变器的诸多控制方案中，比例积分（proportional integration，PI）控制是最常见的［7-10］，然而PI控制器的增益仅在直流频率处为无穷大，由于逆变输出电压为交流信号，PI控制器无法实现逆变电压的无差跟踪。重复控制的思想是将系统外部输入信号嵌入控制器形成反馈控制，因其具有交流信号跟踪精度高的优点而被广泛应用于逆变器控制系统［11-15］，它首先构建一个周期延时的误差信号正反馈，进行误差累加，再根据该累加信号的值实时调节被控对象，直到误差降为0，控制器输出信号幅值恒定为止，然而，控制上一个周期的延迟导致动态性能差的问题，是重复控制难以解决的瓶颈。谐振控制器实际上是某一特定频率周期信号的内模，将其应用至逆变器控制环路，可使控制回路在特定频率处增益无穷大，因此谐振控制器可以实现对单一频率的交流信号无静差跟踪［16-19］，但是当被跟踪交流频率变化时，控制器增益明显下降，影响逆变器的跟踪性能。文献［20-22］引入准比例谐振（proportional resonant，PR）控制器，在控制精度范围内以降低谐振频率处增益为代价，获得谐振频率附近高增益，提升了控制器的频率适应性。

另外，由于实际逆变器IGBT 器件和正负母排特性不对称在所难免，必然造成逆变输出电压直流偏置。对于应用于UPS 的逆变器，通常在输出端增设变压器以实现和负载安全电隔离，由于电力变压器绕组内阻很小，只要逆变输出存在直流偏置，就会在变压器线圈产生较大的直流电流，导致铁芯饱和，增大了变压器的损耗，危及负载安全运行。文献［23］设计了一种饱和电抗器，使其额定条件下在磁化特性拐点处运行，以检测变换器输出端的电压直流分量，并将其叠加至电网电流，作为并网逆变器的反馈信号，抑制并网逆变器电流的直流分量，但该直流检测电路的电抗器体积大，且存在较大的损耗。文献［24-25］引入自适应复数滤波器和带通滤波器解决直流偏置对弱电网直流偏置对锁相环的影响，但此类方法未考虑检测电路对直流偏置的检测误差问题。文献［26］在每一基波周期结束时求取脉冲调制（pulse width modulation，PWM）信号在本周期内的平均值，将其与电压反馈信号一道送到指令比较环节，完成直流偏置抑制，该方法也未考虑检测电路对直流偏置的检测精度问题。

在前述分析的基础上，本文采用输出电压、电感电流双闭环的逆变控制方案，电流内环采用比例控制器阻尼逆变系统的谐振峰值，为了获得高电能质量的输出，电压外环采用比例-积分-谐振（quasi proportional integral resonance，PIR）控制器，并详细推导了电流、电压环路控制器的设计方法；其次，详细分析了传统电压检测电路对直流偏置的检测精度问题，在传统双环控制的基础上，设计了直流偏置检测电路和输出电压直流偏置控制环路；最后对所提控制方案和设计方法进行了实验验证。

1 单相逆变器数学模型

本文以应用于三相UPS 的逆变器为例进行讨论，UPS 一般为三相四线制结构，每一相逆变电路独立运行，可以看成由3 个单相电路组成，分析其中任意一相即可。单相逆变电路拓扑如图1 所示，是由两个IGBT 器件组成的半桥和LC 滤波器两部分组成，图中L和C分别为滤波电感和滤波电容；r为考虑IGBT 器件、电感、开关等电器元件的等效内阻；iL和io分别为电感电流和负载电流；uo为逆变器负载电压；uao为逆变输出电压；Udc为直流电压；直流侧正负母线电容分别为Cdc1和Cdc2。

图1 单相逆变器拓扑Fig. 1 Topology of single-phase inverter

本文建立单相逆变器复频域下，以复频率s为变量的数学模型，首先由逆变器负载端结点M的KCL方程，可得：

式中：uo（s）、io（s）和iL（s）分别为频域下的负载电压、负载电流和电感电流。

再由回路KVL方程可得：

式中：uao（s）为频域下的逆变器输出电压。

如果逆变器采用双极性SPWM调制，有：

式中uc（s）和Utri分别为调制信号和三角载波峰值。

根据式（1）—（3），将调制信号uc（s）作为输入，负载电压uo（s）作为输出，负载电流io（s）作为扰动，可以得到单相逆变器的结构框图如图2所示。

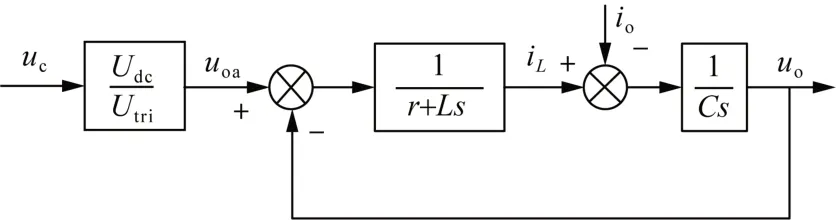
图2 单相逆变器模型框图Fig. 2 Block diagram of single-phase inverter model

2 单相逆变器双环控制与设计

双环控制框图如图3 所示。其中，电感电流内环采用比例控制器，改善控制系统的模型，提升系统的稳态性能；电压外环采用准PIR 控制器，保证对输出基波信号的跟踪和直流偏置信号的控制。图中：uref和iLref分别为电压控制环路和电流控制环路的指令信号；Gd（s）为考虑到SPWM 环节和数字计算延时的传递函数，对应的延时时间Td=1.5Ts，Ts为开关周期［27-28］，Gd（s）可表示为：

图3 逆变器双环控制框图Fig. 3 Block diagram of the dual-loop control in inverter

令电流控制环路比例控制器增益为kc，电压控制环路准PIR控制器的传递函数GPIR（s）为：

式中：kp和ki分别为准PIR 控制器的比例和积分增益；kr为谐振控制器的增益；ωc为谐振控制器的开环截止角频率；ω0为谐振角频率。

2.1 电流内环控制器设计

根据汇聚点后移的原则，逆变器双环控制框图3可等效为控制框图4。从图4可以看出，电流内环比例控制器类似一个虚拟阻抗Z（s）。

图4 逆变器等效双环控制框图Fig. 4 Equivalent diagram of the dual loop control in singlephase inverter

根据欧拉公式，可知：

当1/(2Ts)>ω> 1/(6Ts)时，Re[Z(jω)]< 0，虚拟阻抗实部为负，电压控制环路变为非最小相位系统，控制系统的稳定性受到较大影响。因此，基于系统稳定性考虑，电流控制环路带宽ωg应满足ωg<1/（6Ts）。

逆变输出电压和电感电流指令之间的传递函数为：

由式（8）可知，电流控制环路为一个二阶系统，阻尼系数ζ可以表示为：

式（9）说明，电流控制环路引入比例调节器后，增加了系统的阻尼系数，且阻尼系数随着比例调节器的增益kc的增加而增大。

另一方面，为了确保电流控制环路稳定，必须使控制环路的相位裕度（phase margin， PM）和幅值裕度（gain margin， GM）为正，即：

式中ωp为电流控制环路相位在-180 °时对应的截止角频率。

图5 为电流控制环路的相位裕度KPM和阻尼比ζ随电流控制器增益kc变化的曲线，阻尼比随着kc增加而增大，但相位裕度却随之降低。

图5 相位裕度KPM和阻尼比ζ随kc变化曲线Fig. 5 Variation curves of phase margin and damping ratio ζ with kc

最后，考虑到控制环路的动态性能和电流开关纹波的抑制效果以及前述虚拟阻抗特性，电流控制环路的穿越频率ωg取为开关频率的1/6 以下。本文针对10 kW 单相逆变器，取滤波电感L=1.2 mH，滤波电容C=80 μF，电感及器件的等效电阻r=0.2 Ω，开关频率fs=10 kHz，令电流环路穿越频率fg=1 500 Hz，得到：

计算得kc=0.8。

图6 为所设计的比例控制器参数下电流控制环路的幅值-相位曲线和Nichols 图，可以看出电流控制环路的相位裕度KPM=55 °，KGM>0，控制环路稳定。

图6 电流控制系统幅值-相位曲线和Nichols图Fig. 6 Amplitude-phase plot and Nichols chart of current control system

2.2 电压外环控制器设计

由图3 所示的逆变器控制框图，可以得到电压控制环路的开环传递函数GU（s）为：

电压控制环路准PIR 控制器的比例增益kp决定电压环路的带宽，积分增益ki决定环路的直流增益，抑制输出直流干扰，准谐振控制器R 决定指令信号频率处的增益，影响控制系统的静态性能。图7为比例系数kp=0.8，谐振控制器的截止角频率ωc=4，积分系数ki和谐振增益kr变化时准PIR 控制器的伯德图。

图7 准PIR控制器波特图Fig. 7 Bode plot of quasi-PIR controller

图中ki从20~100，kr在20~180 之间变动，可以看出，积分系数和谐振增益仅影响直流和谐振控制器谐振频率处的增益，而对高频段的增益和相位基本无影响，可以认为准PIR 控制器的比例环节、积分环节和准谐振环节解耦［25］，因此准PIR 控制器各环节可单独设计。

1） 比例增益kp设计

根据前述设计的电流环路比例调节器的结果，忽略积分和谐振控制器，得到电压控制环路的开环传递函数GU1（s）为：

控制环路的相位裕度约束为：

式中ωug为电压控制环路的穿越角频率。

再考虑开关次谐波的滤波效果以及控制环路的动态性能，选择电压环路的穿越频率fug为基波频率fo的10 倍到开关频率fs的1/10 之间，本文取fug=400 Hz，得到比例系数kp=1.2，由式（15）得到对应控制环路的相位裕度KPM=55 °。

2） 积分增益ki设计

在前述电压环路比例控制器参数kp设计的基础上，由控制框图4 得到含PI 控制器的电压控制环路开环传递函数GU2（s）为：

为了确保控制系统稳定，令电压控制环路相位裕度不低于60 °，即：

解得ki<300，本文选ki=150，算得KPM=54 °。

3） 谐振增益kr设计

考虑到频率适应性，准谐振控制器的截止频率ωc一般为4~6 rad/s［29］，本文取ωc=4 rad/s。谐振增益可以根据谐振频率处的误差确定，含准PIR 控制器的逆变输出电压误差传递函数eu（s）为：

设置逆变输出50 Hz 频率处的稳态误差为0.5%，即：

计算得到kr=98。

考虑延时环节时的电压控制环路传递函数GUd（s）为：

图8 为按照本文设计的参数，考虑延时后电压控制环路幅值-相位曲线和Nichols 图，可以看出电压控制环路的相位裕度KPM=50 °，带宽为500 Hz。

图8 电压控制系统幅值-相位曲线和Nichols图Fig. 8 Amplitude-phase plot and Nichols chart of voltage control system

3 单相逆变输出直流偏置原因及抑制方法

3.1 逆变器输出直流偏置的原因

图1 所示的半桥逆变电路IGBT 器件参数和直流侧正负母线电压不一致现象在所难免；此外，为了防止逆变桥上下功率器件直通，通常在驱动电路设置死区时间，将导致逆变输出PWM 波形不对称，这些因素势必造成输出侧产生较大的直流成分。虽然电压控制环路的PIR 器对直流信号有一定的抑制作用，但由于受到电压检测精度的限制，输出电压的直流分量依然存在。

在逆变器控制系统中，输出电压信号是由检测调制电路送至DSP 的模数转换器（analog to digital converter，ADC），再进行数字控制。对于n位ADC，其最低分辨率ε为：

式中UAD为ADC 的最大转换电压值。考虑逆变器输出过压保护等实际因素，在设计电压采样电路时，最大采样值一般设计为额定电压的1.15 倍，额定输出电压有效值为220 V，对应的最大采样电压峰峰值为715 V，DSP控制器的ADC一般为12位，即使忽略采样和调理电路的误差，由式（19）可知，电压采样通道的最低分辨率为175 mV，电压控制环路积分控制器无法抑制检测精度以下的直流分量，这将引起逆变器输出侧变压器和滤波电感等磁元件饱和，产生不利影响。

3.2 逆变器输出直流偏置检测电路

为了进一步抑制逆变器输出的直流偏置，本文首先设计了输出电压直流偏置检测电路，在此基础上，构建直流偏置控制环路，进一步抑制逆变输出的直流分量。

直流偏置检测电路应在大幅衰减逆变电压50 Hz 交流成分的基础上，使直流分量信号通过，因此，可将其设计成一个低通滤波器，检测电路如图9 所示，包括第一级衰减电路、反相电路、第二级衰减+偏置电路和输出限幅4个部分。

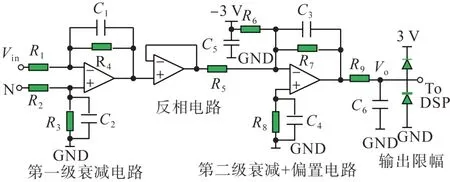
图9 直流偏置检测电路Fig. 9 DC bias detection circuit

考虑差模信号的抑制，将第一级衰减电路设计成差分电路，并使R1=R2=R3=R4，R5=R7=R8，C1=C2=C3=C4=C，得到检测电路的输入、输出信号之间的传递函数HU（s）为：

式 中 ：b1=R4R7R9C1C3C5，b2=R4R9C1C5+R7R9C3C5+R4R7R9C1C3b3=R4C1+R7C3+R9C5。

取R1=500 kΩ，R5=1 MΩ，R6=2 MΩ，R9=1 kΩ，C=1 μF，C5=C6=0.1 μF，得到直流偏置检测电路传递函数波特图如图10 所示。可以看出，采用本文所设计的直流分量检测电路，逆变输出电压基波分量衰减了90 dB，而对直流分量无衰减。该直流偏置检测电路可靠性高，体积小，且基本无损耗。

图10 直流偏置检测电路幅频特性曲线Fig. 10 Amplitude frequency characteristic curve of DC bias detection circuit

3.3 逆变器双环改进控制

图11 为考虑逆变输出直流偏置抑制的改进双环控制系统框图，在图4 所示的双环控制系统基础上引入直流偏置控制回路。首先由直流偏置检测电路提取逆变输出直流偏置的信息udc，再和指令信号0 比较，经直流控制环路的PI 控制器Gdc（s）作用，将其输出叠加至电压控制环路的输入端，形成电压控制环路指令信号ur，调整逆变输出的直流偏置。

图11 逆变器双环改进控制框图Fig. 11 Block diagram of the modified dual-loop control in inverter

直流偏置控制环路PI 调节器的传递函数Gdc（s）为：

式中kdcP和kdcI分别为PI控制器的比例和积分增益。

由图11，结合式（20）的电压控制环路传递函数GUd（s），可以得到含直流偏置控制环路的开环传递函数Hdc（s）为：

由于准PIR 控制器在直流和谐振频率处增益为无穷大，在设计直流偏置控制环路时，可近似认为电压控制环路闭环增益为1，将Hdc（s）简化为：

输出电压直流偏置一般呈现低频特性，可将直流偏置控制环的带宽设计为1 Hz，将PI控制器的转折频率设计为0.1 Hz，以避免积分环节对直流偏置控制环路带宽频率处相位造成影响，计算可得kdcP= 3.9，kdcI= 2.4。图12 为按照本文设计参数得到的直流偏置控制系统幅值-相位曲线和Nichols图，可以看出直流电压控制环路相位裕度KPM=55 °，控制系统稳定性较好。

图12 直流偏置控制系统幅值-相位曲线和Nichols图Fig. 12 Amplitude-phase curve and Nichols diagram of DC bias control system

4 仿真和实验验证

为了验证所提逆变器控制策略的正确性，进行了仿真和实验验证。图13 为整流+逆变的在线式UPS 主电路结构，三相四线制整流器为单相逆变器提供直流电压Vdc，直流母线中点O与电网中点N相连，并同时和逆变器负载连接，直流侧正负母线电容取为Cdc1=Cdc2=4 700 μF。

图13 系统主电路结构Fig. 13 Structure of main circuit

4.1 仿真验证

根据图13 所示的主电路结构，利用MATLAB/Simulink 搭建仿真模型，系统主电路和逆变器各控制器参数如表1所示。

表1 逆变器系统参数Tab. 1 Parameters of inverter system

图14 为加直流偏置控制环路前后逆变器空载和满载仿真波形，输出电压稳定，电压总谐波畸变率（total harmonic distortion，THD）均在1.5%以内。未加直流偏置控制时，输出电压直流偏置为-400 mV，该值与逆变电压相比很小，因此直流偏置对逆变输出波形质量影响较小，但引入直流偏置环路后，逆变电压直流偏置降至0。

图14 稳态仿真波形Fig. 14 Steady state simulation waveform

图15（a）—（d）为传统双环控制和双环加直流偏置控制的逆变器空载和满载之间切换的动态波形，可以看出，在本文设计的控制器参数下，逆变器动态调节时间在15 ms以内，超调量小于2%，且直流偏置控制对逆变器动态无影响。图15（e）为逆变器在传统双环控制下满载运行3 s 时，引入直流偏置控制值环路，逆变输出电压直流偏置波形，可以看出，加入直流偏置控制后，经过6 s 调节时间后，输出电压直流偏置由-400 mV 变为0 mV，直流偏置控制环路具有较好的动静态性能。

图15 动态仿真波形Fig. 15 Dynamic state simulation waveform

4.2 实验验证

为了进一步验证本文所提控制策略的有效性，搭建了10 kW 单相逆变器硬件平台进行实验验证。该平台主要包括由IGBT 模块组成的单相半桥及其驱动电路，直流母排，LC 滤波器，输出断路器等部分。逆变器硬件及其控制器参数和表1 相同，以TMS320F2812芯片为控制核心。

基于本文所设计的控制方案和参数，直流偏置控制引入前后逆变器稳态时的输出电压和电流波形如图16 所示。可以看出，无论空载还是满载，逆变输出的波形稳定，且THD 均在1.2%以内，输出精度小于0.8%，不同负载下的逆变输出电压质量较好，且直流偏置控制环路对逆变器的稳态性能基本无影响。

图16 稳态实验波形Fig.16 Steady state experimental waveform

图17 为逆变器直流偏置引入前后空载和满载之间的切换波形，负载切换时，逆变输出电压超调量小于2%，调节时间在15 ms以内，控制系统具有较好的动态性能，且直流偏置控制对系统动态基本无影响。

图17 动态实验波形Fig.17 Dynamic experimental waveform

图18（a）为直流偏置控制环路引入前后逆变器满载时输出电压及其直流偏置波形，从图18（b）和图18（c）的放大波形可以看出，传统双环控制下输出电压直流偏置接近-200 mV，引入直流偏置控制后，输出电压直流偏置绝对值在30 mV 以内，直流偏置得到显著抑制。

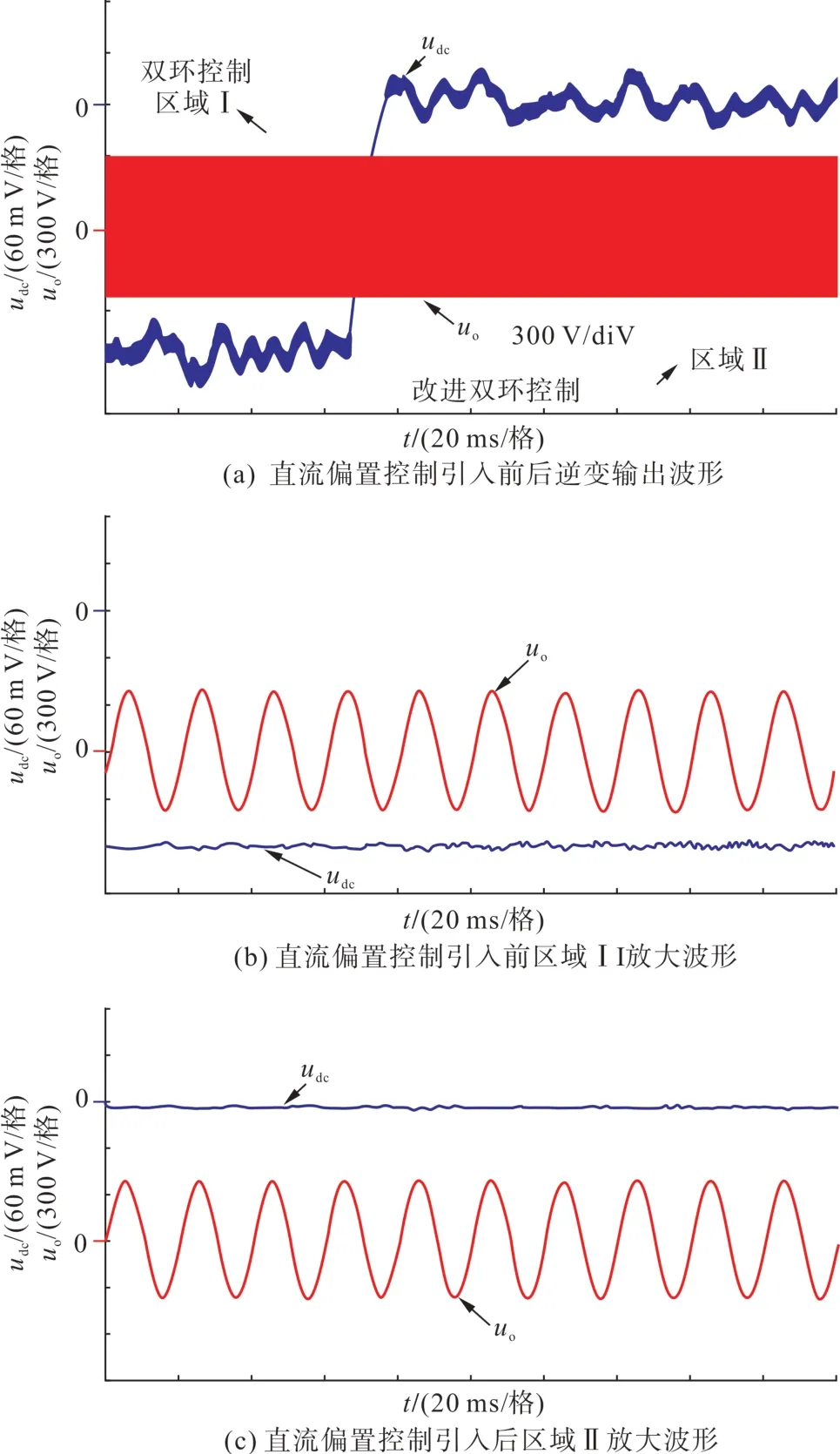
图18 不同控制方式下输出直流偏置对比波形Fig. 18 Comparison waveforms of output DC bias based on different control strategies

5 结语

本文针对单相逆变器的电压、电流双闭环控制策略，分析了电流控制环路比例控制器和电压控制环路准PIR 控制器的参数设计和环路稳定性。在此基础上，揭示了传统双环控制无法抑制逆变输出直流偏置的机理，并设计了直流偏置信号采样电路和直流偏置控制环路，最后给出了系统仿真和实验验证。仿真和实验结果表明：采用本文提出的改进控制方法，阻性负载下逆变器输出电压THD 在1.2%以下，空载到满载切换时，超调量低于2%，逆变器控制系统具有良好的动静态性能，同时，输出电压的直流偏置绝对值从200 mV 大幅降至30 mV 以内，改善了逆变器的输出性能。