多轴隧道机器人非线性环形耦合协同控制
2023-09-21杨贤昭黄晶晶刘惠康王立辉
杨贤昭,黄晶晶,刘惠康,王立辉
(武汉科技大学冶金自动化与检测技术教育部工程研究中心,湖北 武汉 430081)
1 引言
苏通GIL管廊工程为单项越江工程,项目总长度5.8km。工程项目采用长距离特高压“GIL”气体绝缘管道输电,采用GIL管廊(隧道)过江。项目采用两1100kV GIL敷设于地下管廊中穿越长江,两回GIL管道采用垂直布置,分开布置在管廊两侧。由于是特高压变电站及其输电线路的各项巡检工作,采用人工进行养护是常规做法,能够发现管廊在运行过程中存在的问题并能及时处理。然而路线过长,需要检查记录项目过多,不能做到全面细致的检查,比较隐秘的缺陷和故障无法发现;无法及时发现管壁温度以及是否漏电放电,更不能测量空气中的有毒气体是否会对巡检人员的健康造成危害,也无法及时发现一些不法分子的破坏或盗窃行为,工作效率低下,并且特别危险。变电站巡检人员对于上述诸多情况,只是通过眼睛、耳朵等感官对运行电力设备进行简单的定性判断,难以准确、快速地发现变电站设备存在的隐患或缺陷[1]。为保障管廊内设备的安全运行,项目采用智能化设备,实现对管廊内设备实时、高效的在线监控。对于管廊内的各种设备巡检,项目采用智能巡检机器人。智能巡检机器人应用广泛,电力系统的各个环节随处可见,比如各种变电所,各类发电厂,以及冶金行业等领域。智能巡检机器人取代了体力劳动,可以独立完成复杂,困难,危险以及重复性工作,减少了人员安排,节省了成本,降低了风险,提高了电网的智能度。然而要想使得智能巡检机器人系统实现准确快速的位置控制,就必须制造精密的零部件以及研究先进适用的多轴控制算法。
近年来国内外对于多轴同步控制技术非常重视,已经提出了许多用于各类机器人控制系统的位置和轨迹跟踪控制的策略。目前使用的多轴同步控制方案主要两种:一种是常规控制方式,一种是耦合控制方式。常规方式使用的主要有主从控制方式。耦合方式主要有交叉耦合、偏差耦合、环形耦合等同步控制方法。一般的控制系统精度要求不高,追求简单易用,多会使用主从同步控制方式。而实际生产中,对于精度要求比较高地方,主从控制方案就无能为力,此时必须提高机器人的控制精度,于是文献[2]在1980率先提出了一种交叉耦合控制策略,并将其应用到机床,控制效果不错。交叉耦合控制与传统控制的主要区别在于引入了同步误差,该误差表示多个制动器之间的协调程度,将其用于控制器中,以便在过渡阶段调节机器人轨迹。上述交叉耦合控制仅能解决两轴之间同步控制问题,而无法解决三轴及其以上多轴之间同步控制问题。2003年文献[3]提出一种偏差耦合控制策略,使用该方法来实现多轴同步控制。文献[4]提出了一种多轴位置同步的自适应耦合控制算法,通过位置误差和同步误差的反馈,将交叉耦合技术引入自适应控制设计,使得位置误差和同步误差的渐近收敛到零。文献[5]将交叉耦合技术应用到双轴数控机床中,减小了同步误差,提高了机床的加工精度。
相比较于其他同步控制方式,环形耦合控制凭借其加良好的控制性能,很好地解决两轴以上的多轴之间的同步误差。文献[6]提出了一种基于环形耦合的多电机同步控制方案。其控制结构更加简单,方便实现,同时兼顾了控制系统的同步性能。文献[7]将积分分离PID算法多轴同步滑模控制,更好地实现系统的跟踪和同步性能。
当前,现有的无模型同步控制器都是基于PID 的方案。文献[8]提出了一种通过将交叉耦合控制集成到通用的PD控制架构中,实现多轴系统位置控制同步控制。文献[9]通过将PD控制与饱和PI同步控制相结合,为机器人机械手开发了一种集成控制器。然而,尽管这些无模型方案具有简单的控制器结构和易于实现的优点,但实验比较研究表明当系统动态模型可靠时,基于模型的同步控制器比无模型方案具有更好的性能[10]。文献[11]设计了一种六轴工业机器人的非线性同步方案,较好地提高了机器人的轨迹跟踪精度。
为了提高智能巡检机器人的控制精度,引入新型近似势能函数,并与传统的N-PD控制相结合,同时改进同步控制算法,得到一种新型N-PD环形耦合同步控制方案,与传统的PID控制相比,控制器结构更加简单,易于实现,方便应用。同时,系统的位置误差能够快速收敛到零,减小了多轴之间的同步误差,智能巡检机器人同步控制效果提升明显。
2 控制系统模型与分析
一般地,忽略摩擦和外部干扰,n自由度的智能机器人的动力学模型为[12]:
式中:q—轴位置矢量;轴速度矢量轴加速度矢量;M(q)—对称正定惯性矩阵;D(q,̇)—科氏力矩阵;Gq—重力矩阵;τ—各轴力矩矢量。
如式(1)所示的机器人系统,具有以下结构特征:
(1)∀q∈Rn,惯性矩阵M(q)是对称正定矩阵。即:
式中:λm—惯性矩阵的最小特征值;λM—最大特征值。
(2)D(v,ξ)μ=D(v,μ)ξ是向心力和哥式力矩阵,满足:
(3)̇(q) - 2D(q,̇)是反对称矩阵,即:
3 环形耦合控制方案
环形耦合同步控制方案是在交叉耦合的基础上拓展得到的。通常情况下,定义同步误差是有很多选择的,但是在工程实践中多会考虑到,在可控范围内尽可能的简单易用,同时实现跟踪误差和同步误差渐进收敛。因此提出了一种通用的位置同步误差:控制系统中每一对相邻轴的差分位置误差。在这种控制策略下,保证了位置误差和同步误差的渐近收敛性,同时可以改善系统的暂态同步性能。在此基础上提出了下面的环形耦合控制策略,三轴隧道巡检机器人的同步控制方案,如图1所示。
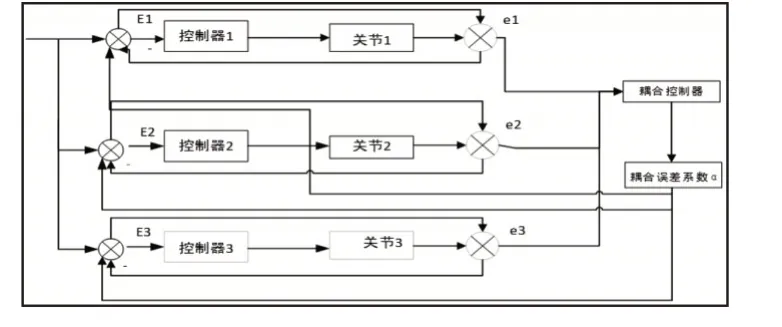
图1 智能巡检机器人环形耦合控制策略Fig.1 Loop Coupling Control Strategy of Intelligent Inspection Robot
系统的位置误差公式:控制对象的实际位置qi(t)与期望位置qid(t)之差,即:
同步误差定义为被控轴与其相邻两轴位置之差:
式中:Δei(t)—控制系统第i轴同步误差。假若使得所有的同步误差为0,那么式(7)中每一个同步误差都必须是0,由此可得:
为了使得同步误差具有通用性,将其改写成下面的形式:
式中:T—同步变换矩阵T=TT。
式中:I—单位矩阵;α—耦合系数。
当0 <α≤1,α越大,机器人系统同步控制效果越好。当e→0,同时Δe→0,那么E→0,这样就达到了机器人多轴同步控制的目的。
4 控制器设计
首先引入下面一类近似势能函数[13]:
式中:ρ0,δ0∈(0,1];β0>δ0—设计参数。
式中:sgn(⋅)—符号函数。
式(13)与式(14)描述是非线性函数Z(t)和z(t),具有如下性质:
(1)如t≠0,那么Z(t) >0;如t= 0,那么Z(t) = 0和z(t) = 0。
(2)Z(t)连续二阶可微,z(t)之于t为单调增函数。
(3)当t≠0,至少有一个正常数k>0,使得下式成立:
(4)对于t≠0,存在正常数k1>0,使得下式成立:
应用简单运算即可证明上述性质。
一般地,机器人的PD控制律为:
线性PD同步控制控制算法为:
为了消除静差,克服较大振荡,提高机器人的位置控制精度,由式(15)和式(16)及其引理,设计非线性PD同步控制律为:
式中:KE—同步增益矩阵。
将式(19)代入式(1)可得闭环系统为:
式(20)唯一静态平衡点是[eTėT]T= 0 ∈ℜ3n。
对于闭环系统式(20),满足下面的定理,会使得闭环系统的位置误差全局渐进稳定的。
为了证明所提出的控制律的有效性,提出如下Lyapunov函数:
由式(2)和式(15)可得:
将式(27)带入式(26)并应用式(22)和式(23)可得:对于任意的[eṪTΔeT]T≠0,有:
式(13)可知,Z(x)是径向无界函数,故而所选的Lyapunov函数V是一个正定函数。
对式(26)关于时间t进行微分,并将式(20)带入,再应用式(5),有:
利用式(2)和式(14)得:
由式(12)得:
当式(22)~式(24)以及a为任意足够小的正常数,则̇≤0。z(e) = 0,e= 0,同时应用LaSalle不变性原理可以得到,所设计的闭环控制系统是全局渐进稳定的,因而说明了所提出的控制策略可行性。
5 仿真实验结果分析
为了验证所提出控制算法的有效性,使用MATLAB/Simulink建立仿真模型,进行仿真实验。设3自由度智能巡检机器人起始位置是零,期望位置qd(t)均为1rad。根据仿真所得的控制最佳参数为:
智能巡检机器人的三个关节位置跟踪曲线,如图2~图4所示。由下面三幅图可得,PD(线性PD)、非线性PD(N-PD)、非线性PD(N-PDRC)三种不同控制算法相比较,在控制参数一样的情况下,N-PDRC控制方法位置误差最小,且能最快到达期望位置。

图2 PD算法位置跟踪误差曲线Fig.2 The Tracking Errors about the PD Algorithm Position
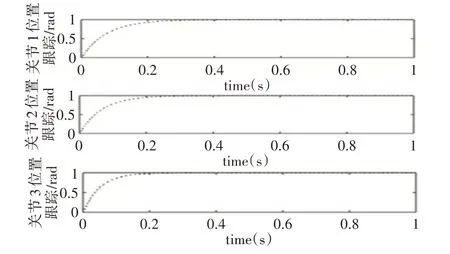
图3 N-PD算法位置跟踪误差曲线Fig.3 N-PD Algorithm Position Tracking Error Curve

图4 改进N-PD环形耦合同步控制算法位置跟踪误差曲线Fig.4 Improved N-PD Loop Coupling Synchronization Control Algorithm Position Tracking Error Curve
由图5~图6可以清楚地得到,控制参数一样时,N-PDRC同步控制算法LPD控制算法进行对比,显然前者使得控制系统位置误差更小,同时单位时间内收敛速度更快。

图5 N-PD算法位置误差曲线Fig.5 Position Error Curve of N-PD Algorithm

图6 改进N-PD环形耦合同步控制位置误差曲线Fig.6 Improved N-PD Loop Coupling Synchronous Control Position Error Curve
由图7~图8知,当控制参数一定时,与N-PD控制算法相比,N-PDRC 同步控制方法下的同步误差减小明显,而且收敛时间短。由表1可知,N-PDRC同步控制方案比N-PD同步控制策略的作用下,控制系统同步误差平均缩小87.1%,控制器响应速度明显加快。

表1 2种控制策略的同步误差比较Tab.1 Comparison of Synchronization Errors of Two Control Strategies

表2 2种控制策略的收敛时间比较Tab.2 Comparison of Convergence Time of Two Control Strategies

图7 PD环形耦合同步控制算法同步误差曲线Fig.7 PD Ring Coupling Synchronization Control Algorithm Synchronization Error Curve

图8 改进非线性PD环形耦合同步控制算法同步误差曲线Fig.8 Synchronization Error Curve of Improved N-PD Ring Coupling Synchronization Control Algorithm
由表可得,N-PDRC同步控制策略与N-PD同步控制策略进行对比,收敛时间平均缩短78.7%,各关节同步效果提升显著。
6 结论
为了提高隧道智能巡检机器人的位置跟踪以及同步控制性能,对机器人多轴同步控制方法进行了研究,提出了一种基于系统动力学模型和环形耦合控制方法的非线性PD同步控制方案。通过李亚普洛夫方法和LaSalle不变性原理,分析了新的控制策略的稳定性。最后,通过对几种算法仿真对比研究得到,所提出的新型非线性PID环形耦合同步控制算法具有良好的同步性能,减小了机器人多轴之间的位置误差以及同步误差,明显加快了系统的响应速度,提高了多轴系统的同步性能,验证了所提出控制算法的可行性。
