不同稀疏基对单像素相机矩阵性能的影响

2023-09-21吴小龙魏晟弘

机械设计与制造 2023年9期

伍松，吴小龙，魏晟弘

（1.广西科技大学机械与交通工程学院，广西柳州 545006；2.广西汽车零部件与整车技术重点实验室（广西科技大学），广西柳州 545006）

1 引言

压缩感知的核心思想是能够减少测量点数并可以精确或者近似精确的恢复出原始信号［1-2］。Rice大学依据压缩感知理论提出的单像素相机系统有一个很明显的特点就是多光谱波段成像，这是由压缩感知理论和数字微镜器件（Digital Micromirror Decive，DMD）以及光电探测器的硬件特性而来的。单像素相机系统是压缩感知理论的一个重要应用，它通过DMD接收光信号，最后通过光电转换把信号输入电脑重构出图像。它不仅打破了奈奎斯特采样定理采样过多的局限，也打破了传统的成像系统中只能在局部波段进行成像的限制。此外，该系统的出现为此前压缩感知中常用的测量矩阵，如：高斯矩阵、伯努利矩阵和哈达玛矩阵等难以硬件实现的问题提供了解决方法。DMD相当于压缩感知中的测量矩阵，可以设定成不同的序列，对应的测量矩阵也不一样，在DMD中测量矩阵的元素均为0或者1，1表示接收信号，0表示不接收信号。测量矩阵大致可以分为三类，第一类是随机矩阵［3］，第二类是部分正交矩阵［4］，第三类是确定型矩阵［5］。高斯随机矩阵、哈达玛矩阵和伯努利矩阵等都属于压缩感知中常用的测量矩阵，能够很好的满足压缩感知对测量矩阵的要求，但这些矩阵多为稠密矩阵，元素所需的储存空间大，而且由于其非结构化的本质导致其计算复杂，不利于硬件实现。其中，确定型矩阵中的0-1循环矩阵是最容易硬件实现的测量矩阵。

对于离散余弦变换（Discrete Cosine Transform，DCT）［6-7］矩阵和离散小波变换（Discrete Wavelet Transformation，DWT）［8-9］矩阵的研究已经较为丰富，但对于基于这两种稀疏基与单像素相机矩阵构成的重构矩阵以及优化后得到的优化矩阵研究较少。将基于0-1循环矩阵与这两种稀疏基组合得到的重构矩阵和由重构矩阵优化后得到的优化矩阵分别对信号进行重构，对比分析基于这两种稀疏基得到的重构矩阵和优化矩阵对信号的重构效果，基于离散小波变换矩阵得到的重构矩阵以及优化矩阵对信号的重构效果更好。

2 压缩感知理论与单像素相机矩阵

由参考文献［10-11］可知，压缩感知中，可压缩信号模型如下：

式中：y—测量信号，y∈RM；Φ—测量矩阵，Φ∈RM×N，Ψ—稀疏基，Ψ∈RN×N；x—可压缩信号，x∈RN；α—x的稀疏变换域系数，α∈RN；A—重构矩阵；M—测量矩阵的行数；N—测量矩阵的列数。压缩感知的核心过程为数据采集和数据重构。在测量阶段，通过测量矩阵Φ采集到测量数据y；在重构阶段，通过式（1）解算得到变换域系数α，再由式（2）求得信号x。

单像素相机的实物图，如图1所示。光束打到物体上，经过透镜1打到DMD上，再由DMD反射到透镜2，由单点探测器接收光信号，最后经过光电转换将光信号转换为电信号，由采集卡进行采集。其中的核心部件为DMD，其表面由多个小镜子组成，镜面翻转+12°表示接收光信号，在矩阵中用1来表示；镜面翻转-12°表示不接收光信号，在矩阵中用0来表示。所以使用单像素相机矩阵可以更容易将测量矩阵硬件实现。

图1 单像素相机实物图Fig.1 Physical Image of A Single-Pixel Camera

3 基于不同稀疏基的重构矩阵优化前后的性能分析

对基于0-1循环矩阵和DCT矩阵组成的重构矩阵（简称余弦重构矩阵）以及由0-1循环和DWT矩阵组成的重构矩阵（简称小波重构矩阵）分别做行正交化和列单位化的优化运算（在图2～图5中运算100次），由余弦重构矩阵优化得到的优化矩阵简称为余弦优化矩阵，由小波重构矩阵优化得到的优化矩阵简称为小波优化矩阵。主要研究余弦重构矩阵与小波重构矩阵在优化过程中的各自重构矩阵的性质变化，分别从行模极值、相关系数绝对值最大值、服从高斯分布的行列数以及列模来展示，如图2～图5所示。0-1循环矩阵的维度设置为（128×256），初始行放置128个随机分布的1，每一行由上一行向右移动2位得到。

图2 基于余弦重构矩阵和小波重构矩阵的优化矩阵行模极值与迭代次数的关系图Fig.2 The Relationship Between the Extreme Value of the Row Mode of the Optimized Matrix and the Number of Iterations Based on the Cosine Reconstruction Matrix and the Wavelet Reconstruction Matrix

基于余弦重构矩阵和小波重构矩阵在优化过程中，得到的优化矩阵行模的极值与迭代次数的关系图，如图2所示。从图中可知，当迭代次数为20时，余弦重构矩阵的行模最大值逐渐收敛于1.421，当迭代次数为95 时，余弦重构矩阵的行模最小值收敛于1.379；当迭代次数为10时，小波重构矩阵的行模最大值与最小值均收敛于1.414。小波重构矩阵在迭代过程中行模的收敛性要好于余弦重构矩阵在迭代过程中的行模收敛性。

基于余弦重构矩阵和小波重构矩阵在优化过程中，得到的优化矩阵的行和列相关系数的绝对值最大值与迭代次数的关系图，如图3所示。从图中可知，余弦重构矩阵的列相关系数的最大值在迭代过程中均接近于1，余弦重构矩阵的行相关系数的最大值在第10次迭代后收敛于0；当迭代次数为5时，小波重构矩阵的列相关系数的最大值收敛于0.281，行相关系数的最大值收敛于0。小波重构矩阵在优化后得到的小波优化矩阵的列不相关性明显好于离散优化矩阵的列不相关性。

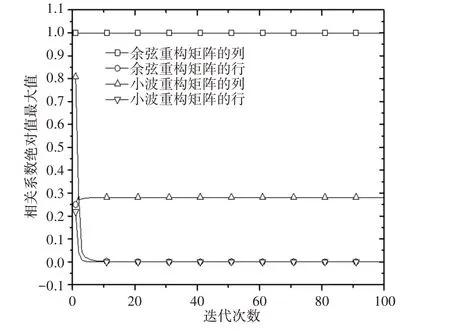
图3 基于余弦重构矩阵和小波重构矩阵的优化矩阵相关系数绝对值最大值与迭代次数的关系图Fig.3 The Relationship Between the Maximum Absolute Value of the Correlation Coefficient of the Optimized Matrix Based on the Cosine Reconstruction Matrix and the Wavelet Reconstruction Matrix and the Number of Iterations

基于余弦重构矩阵和小波重构矩阵在优化过程中，得到的优化矩阵服从高斯分布的行列数与迭代次数的关系图，如图4 所示。从图中可知，余弦重构矩阵服从高斯分布的列数在第2次迭代后迅速收敛为0，服从高斯分布的行数在第2次迭代后也迅速收敛于0；小波重构矩阵的服从高斯分布的列数在第90次迭代后收敛于246，服从高斯分布的行数在第90次迭代后收敛于123。可以看出，小波重构矩阵在迭代过程中行和列服从高斯分布的情况明显好于余弦重构矩阵在迭代过程中行和列服从高斯分布的情况。

图4 基于余弦重构矩阵和小波重构矩阵的优化矩阵服从高斯分布的行列数与迭代次数的关系图Fig.4 The Relationship Between the Number of Rows and Columns and the Number of Iterations of the Optimized Matrix Based on the Cosine Reconstruction Matrix and the Wavelet Reconstruction Matrix that Obey the Gaussian Distribution

基于余弦重构矩阵和小波重构矩阵在优化过程中，得到的优化矩阵的行模极值与迭代次数的关系图，如图5所示。从图中可知，余弦重构矩阵在迭代中的列模最大值与最小值和小波重构矩阵在迭代过程中的列模最大值与最小值均在第2次迭代后收敛于1。从图2～图5可见，由小波重构矩阵迭代得到的小波优化矩阵的性能要明显好于由余弦重构矩阵迭代得到的余弦优化矩阵的性能。

图5 基于余弦重构矩阵和小波重构矩阵的优化矩阵行模极值与迭代次数的关系图Fig.5 The Relationship Between the Extreme Value of the Row Mode of the Optimized Matrix and the Number of Iterations Based on the Cosine Reconstruction Matrix and the Wavelet Reconstruction Matrix

4 实验结果对比分析

为进一步验证余弦重构矩阵与小波重构矩阵，余弦优化矩阵与小波优化矩阵性能的优异。分别用这四种矩阵对高斯稀疏信号进行重构，重构算法采用正交匹配追踪（Orthogonal Matching Pursuit，OMP）［12］算法。每个稀疏度的信号重复实验500次，计算重构概率，如图6所示。计算软件为Matlab2015b。

图6 四种矩阵重构信号的概率与信号稀疏度的关系图Fig.6 The Relationship Between the Probability of the Four Matrix Reconstruction Signals and the Signal Sparsity

由图6可知，小波重构矩阵和小波优化矩阵对信号的重构能力远远好于余弦重构矩阵和余弦重构优化矩阵对信号的重构能力。且当信号稀疏度小于40时，小波优化矩阵对信号的重构概率均为1。

由于0-1循环矩阵是确定性矩阵，该矩阵每一行元素都是由上一行元素移动一定位数得到的，结构相似并且已经确定。0-1循环矩阵为确定性矩阵，而对0-1循环矩阵做离散余弦变换，相当于对测量矩阵各行做离散余弦变换，各列的元素都在相同的频域，因此余弦重构矩阵各列就会非常相似，失去了随机性。即使对重构矩阵做优化也不能提高其随机性，导致各列依然高度相关。对0-1循环矩阵做离散小波变换，是将矩阵中的元素进行多层分解，各列的元素没有处在相同的频域，所以对小波重构矩阵做优化可以使列不相关性变好。